【学习草稿】背包问题
一、01背包问题 图解+详细解析 (转载)
https://blog.csdn.net/qq_37767455/article/details/99086678
:Vi表示第 i 个物品的价值,Wi表示第 i 个物品的体积,定义V(i,j):当前背包容量 j,前 i 个物品最佳组合对应的价值
大概看懂,并根据公式手填了一下表格
最优性原理的基本思想是:一个问题的最优解包含了其子问题的最优解。换句话说,一个问题的最优解可以通过其子问题的最优解递推得到。
最优性原理的应用条件是问题具有最优子结构,即一个问题的最优解可以通过其子问题的最优解递推得到。如果一个问题不具有最优子结构,则不能使用动态规划算法求解。
疑问:原理?为什么是这样的公式呢?
二、【动态规划】01背包问题(通俗易懂,超基础讲解)
https://blog.csdn.net/qq_38410730/article/details/81667885
【好的理解评论?】
我认为那个对于面对一个商品的可能性的描述应该是这样:
1.包的总容量比商品体积小,即使不装其他商品也不可能装得下该商品,此时价值与前i-1个商品的价值一样,即v[i][j]=v[i-1][j];
2.包的总容量大于等于该商品,但若拿出其它商品来获得容量装该商品,此时价值不一定大于前i-1个商品的最大价值,所以在装与不装该商品之间选定一个,即V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i)}
【评论】
j<w(i) V(i,j)=V(i-1,j)
j>=w(i) V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i)}
各位老师,我对这个迭代公式的理解:V(i,j)是指让你最多装j容量的情况下,前i个商品的最大价值,其实是根据题目最终的容量来定义的,也就是让你最多装8容量,求前4个商品的最大价值。那么可以这么理解,第i个商品装不下,那只能装前i-1个商品,V(i,j)就等于V(i-1,j);第i个商品装的下,装和不装两种情况的最优价值是不一样的,取一个最大值,V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i)},V(i-1,j-w(i))+v(i)这个表示我装第i个商品,那么前i-1个商品只能让你最多装j-w(i)的情况下的最大价值。
【】
在状态表V(i,j)中 “j” 就是表示当前背包的总容量。并且在状态转移方程中 V(i-1,j-w(i)) 也并不是说当前背包容量减少了w(i),而是说为了在当前容量为 j 的背包中装入容量为w(i)的物品,所以往前寻找背包容量为 j-w(i) 的状态下的最优值 V(i-1,j-w(i)),这也是状态转移方程的意义所在。
【】
V(0,j):当前背包容量为j,前0个物品最佳组合对应的价值,肯定是0啊(没放东西);
V(i,0):当前背包容量为0,前j个物品最佳组合对应的价值,肯定是0啊(放不进去)。
【???】
动态规划推导不出来递推关系式怎么搞?-- 多看看一些动态规划的例子,感觉一下,这只能多做些题目,就有思路了。
【】
我在手动填表格的时候才真正理解V(i-1,j-w(i))的意思。例如V(4,8),背包容量为8的时候,是否塞入第4个商品的最优V。塞入第4个商品的解为:因为第4个商品的W是5,先在背包腾出5的空间(既定要放进第4个商品),也就是空间为3的最优解加上第4个商品的价值v4。
三、动态规划 原理
1、动态规划中的无后效性(Principle of Optimality)指的是,一个问题的最优解包含了其子问题的最优解,且子问题的最优解不受后续决策的影响。换句话说,一个问题的最优解可以通过其子问题的最优解递推得到,而且子问题的最优解不受后续决策的影响。
这个性质是动态规划算法的核心原理之一,也是其能够高效求解具有最优子结构问题的关键。在动态规划算法中,问题被分解成一系列子问题,并通过递推的方式求解子问题的最优解。在求解过程中,使用了一些启发式规则和策略来指导搜索过程,从而加速搜索并提高搜索结果的质量。同时,通过保存已经求解的子问题的结果,避免了重复计算,提高了算法的效率。
需要注意的是,无后效性是动态规划算法的基本性质之一,但并不是所有问题都具有无后效性。如果一个问题不具有无后效性,则不能使用动态规划算法求解。因此,在使用动态规划算法时,需要先确定问题是否具有无后效性,以避免错误的求解方法。
2、什么是无后效性?
https://blog.csdn.net/qq_30137611/article/details/77655707
所谓无后效性原则,指的是这样一种性质:某阶段的状态一旦确定,则此后过程的演变不再受此前各状态及决策的影响。也就是说,“未来与过去无关”,当前的状态是此前历史的一个完整总结,此前的历史只能通过当前的状态去影响过程未来的演变。具体地说,如果一个问题被划分各个阶段之后,阶段k中的状态只能通过阶段k+1中的状态通过状态转移方程得来,与其他状态没有关系,特别是与未发生的状态没有关系,这就是无后效性
https://baike.baidu.com/item/%E6%97%A0%E5%90%8E%E6%95%88%E6%80%A7/1135283
3、什么是动态规划(Dynamic Programming)?动态规划的意义是什么?
https://www.zhihu.com/question/23995189
四、 完全背包
https://zhuanlan.zhihu.com/p/93857890
完全背包(unbounded knapsack problem)与01背包不同就是每种物品可以有无限多个:一共有N种物品,每种物品有无限多个,第i(i从1开始)种物品的重量为w[i],价值为v[i]。在总重量不超过背包承载上限W的情况下,能够装入背包的最大价值是多少?

相关文章:

【学习草稿】背包问题
一、01背包问题 图解详细解析 (转载) https://blog.csdn.net/qq_37767455/article/details/99086678 :Vi表示第 i 个物品的价值,Wi表示第 i 个物品的体积,定义V(i,j):当前背包容量 j,前 i 个物…...
doxygen c++ 语法
c基本语法模板 以 /*! 开头, */ 结尾 /*!\关键字1\关键字2 */1 文件头部信息 /*! \file ClassA.h* \brief 文件说明 定义了类fatherA* \details This class is used to demonstrate a number of section commands.* \author John Doe* \author Jan Doe* \v…...
)
ChatGLM微调基于P-Tuning/LoRA/Full parameter(上)
1. 准备环境 首先必须有7个G的显存以上,torch >= 1.10 需要根据你的cuda版本 1.1 模型下载 $ git lfs install $ git clone https://huggingface.co/THUDM/chatglm-6b1.2 docker环境搭建 环境搭建 $ sudo docker pull slpcat/chatglm-6b:latest $ sudo docker run -it …...

BLE Mesh蓝牙mesh传输大数据包传输文件照片等大数据量通讯
1、BLE Mesh数据传输现状 BLE Mesh网络技术是低功耗蓝牙的一个进阶版,Mesh扩大了蓝牙在应用中的规模和范围,因为它同时支持超过三万个网络节点,可以跨越大型建筑物,不仅可以使得医疗健康应用更加方便快捷,还能监测像学…...
9.18 QT作业
mainwindow.h QT_BEGIN_NAMESPACE namespace Ui { class MainWindow; } QT_END_NAMESPACEclass MainWindow : public QMainWindow {Q_OBJECTpublic:MainWindow(QWidget *parent nullptr);~MainWindow();signals:void jump(); //自定义跳转信号函数private slots:vo…...
【100天精通Python】Day67:Python可视化_Matplotlib 绘动画,2D、3D 动画 示例+代码
1 绘制2D动画(animation) Matplotlib是一个Python绘图库,它提供了丰富的绘图功能,包括绘制动画。要绘制动画,Matplotlib提供了FuncAnimation类,允许您创建基于函数的动画。下面是一个详细的Matplotlib动画示…...

Linux内核源码分析 (B.x)Linux页表的映射
Linux内核源码分析 (B.x)Linux页表的映射 文章目录 Linux内核源码分析 (B.x)Linux页表的映射一、ARM32页表1、页表术语2、虚拟地址到物理地址转换3、一级页表项4、二级页表项 二、ARM64页表1、ARMv8-A架构2、4KB大小页4级映射 三、Linux内核中关于页表的函数和宏1、查询页表2、…...

机器学习(15)---代价函数、损失函数和目标函数详解
文章目录 一、各自定义二、各自详解三、代价函数和损失函数区别四、例题理解 一、各自定义 1. 代价函数:代价函数(Cost Function)是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均。它用于衡量模型在…...

计算机专业大学规划之双非
亲爱的计算机专业大一学弟学妹们,欢迎来到充满挑战和机遇的大学校园!在经历了小半年的大学生活后,是否会对自己的未来感到一些迷茫,借着前几天给我大一的妹妹聊天的机会,我想发表一下关于我的建议(仅限个…...
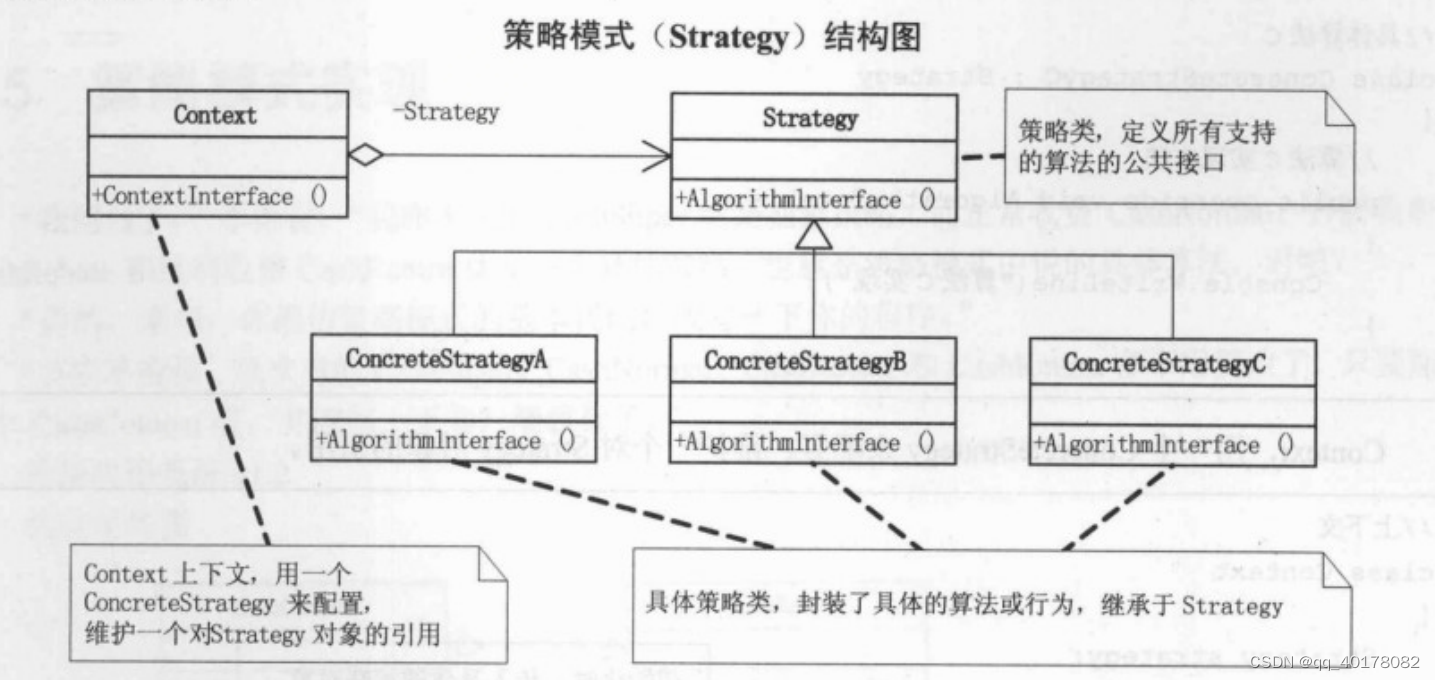
2.策略模式
UML图 代码 main.cpp #include "Strategy.h" #include "Context.h"void test() {Context* pContext nullptr;/* StrategyA */pContext new Context(new StrategyA());pContext->contextInterface();/* StrategyB */pContext new Context(new Strat…...
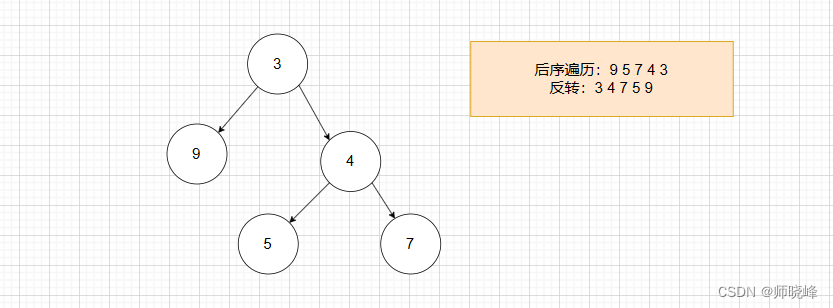
算法通过村第七关-树(递归/二叉树遍历)黄金笔记|迭代遍历
文章目录 前言1. 迭代法实现前序遍历2. 迭代法实现中序遍历3. 迭代法实现后序遍历总结 前言 提示:在一个信息爆炸却多半无用的世界,清晰的见解就成了一种力量。 --尤瓦尔赫拉利《今日简史》 你是不是觉得上一关特别简单,代码少,背…...
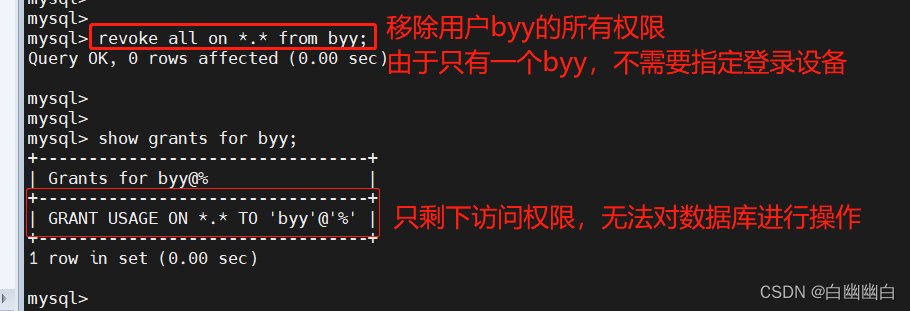
MySQL数据库简介+库表管理操作+数据库用户管理
Mysql Part 1 一、数据库的基本概念1.1 使用数据库的必要性1.2 数据库基本概念1.2.1 数据(Data)1.2.2 表1.2.3 数据库1.2.4 数据库管理系统(DBMS)1.2.5 数据库系统 1.3 数据库的分类1.3.1 关系数据库 SQL1.3.2 非关系数据库 NoSQL…...
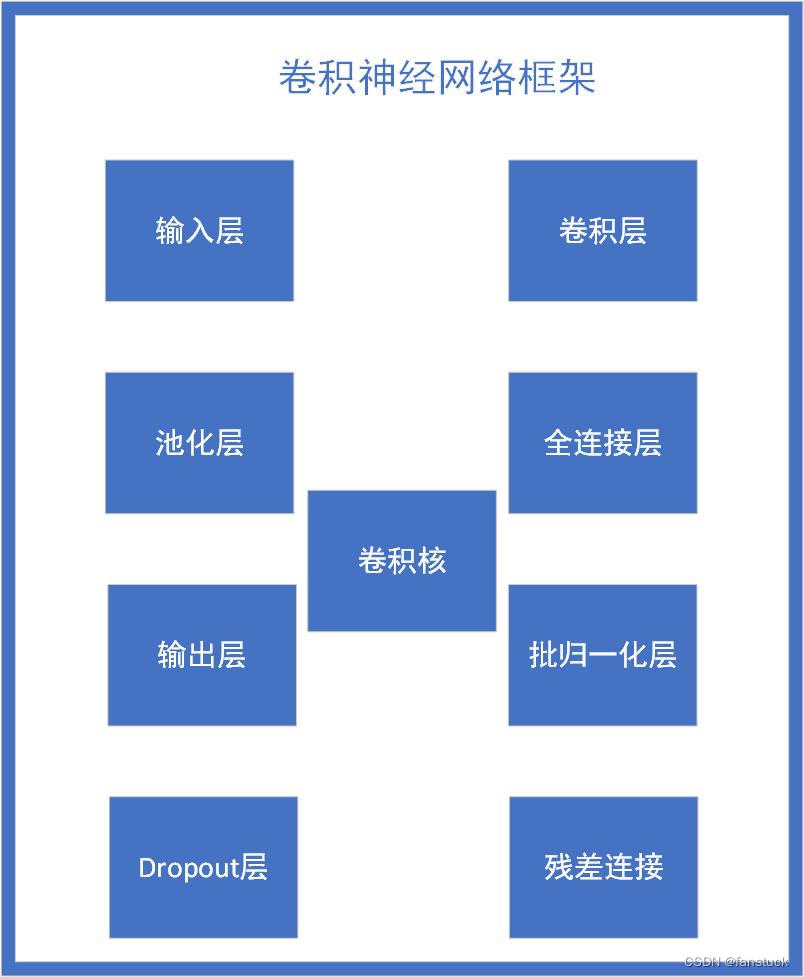
PyTorch实战:卷积神经网络详解+Python实现卷积神经网络Cifar10彩色图片分类
目录 前言 一、卷积神经网络概述 二、卷积神经网络特点 卷积运算 单通道,二维卷积运算示例 单通道,二维,带偏置的卷积示例 带填充的单通道,二维卷积运算示例 Valid卷积 Same卷积 多通道卷积计算 1.局部感知域 2.参数共…...
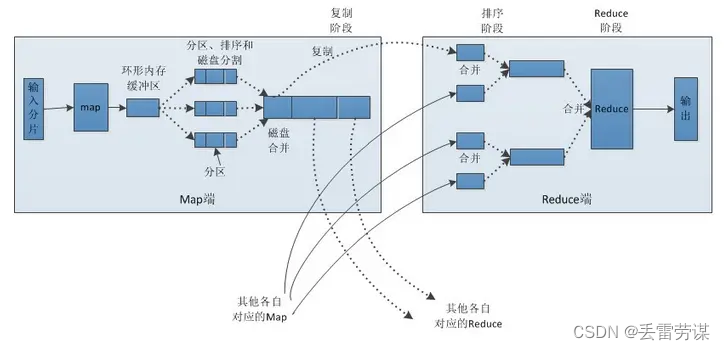
MapRdeuce工作原理
hadoop - (三)通俗易懂地理解MapReduce的工作原理 - 个人文章 - SegmentFault 思否 MapReduce架构 MapReduce执行过程 Map和Reduce工作流程 (input) ->map-> ->combine-> ->reduce-> (output) Map: Reduce...

完整指南:使用JavaScript从零开始构建中国象棋游戏
引言 中国象棋,又被称为国际象棋,是一款起源于中国的古老棋类游戏。本文旨在为大家提供一个简单明了的步骤,教你如何使用JavaScript从零开始构建这款经典的棋类游戏。 1. 游戏简介 在中国象棋中,两方各有一军队,包括…...

PG-DBA培训19:PostgreSQL高可用集群项目实战之Patroni
一、风哥PG-DBA培训19:PostgreSQL高可用集群项目实战之Patroni 课程目标: 本课程由风哥发布的基于PostgreSQL数据库的系列课程,本课程属于PostgreSQL主从复制与高可用集群阶段之PostgreSQL高可用集群项目实战之Patroni,学完本课…...
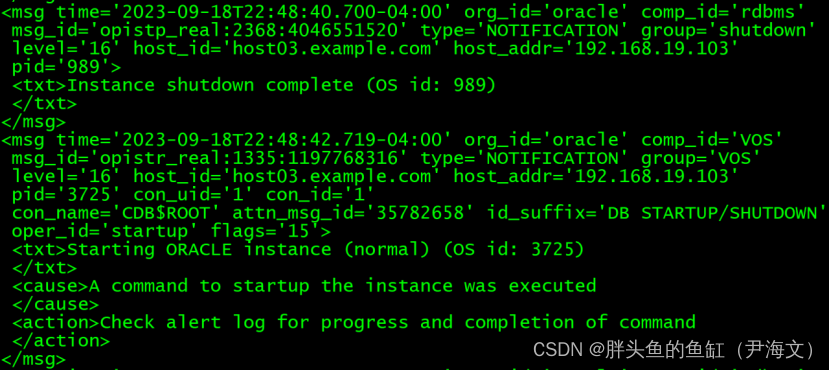
数据库管理-第105期 安装Database Valut组件(20230919)
数据库管理-第105期 安装Database Valut组件(20230919) 之前无论是是EXPDP还是PDB中遇到的一些问题,其实都跟数据库的DV(Database Valut)组件有关,因为目标库没有安装DV导致启动时会出现问题。 1 DV/OLS …...
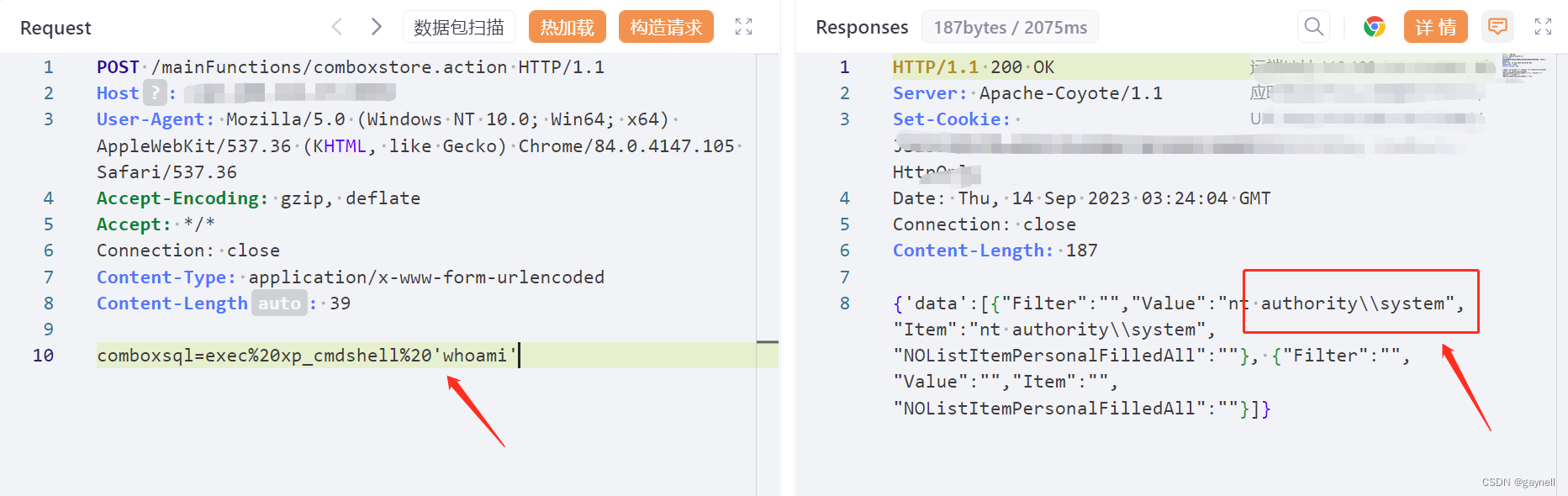
企望制造ERP系统RCE漏洞 复现
文章目录 企望制造ERP系统RCE漏洞 复现0x01 前言0x02 漏洞描述0x03 影响平台0x04 漏洞环境0x05 漏洞复现1.访问漏洞环境2.构造POC3.复现 0x06 修复建议 企望制造ERP系统RCE漏洞 复现 0x01 前言 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播…...

【unity小技巧】Unity 存储存档保存——PlayerPrefs、JsonUtility和MySQL数据库的使用
文章目录 前言PlayerPrefs一、基本介绍二、Demo三、优缺点 JsonUtility一、基本使用二、Demo三、优缺点 Mysql(扩展)完结 前言 游戏存档不言而喻,是游戏设计中的重要元素,可以提高游戏的可玩性,为玩家提供更多的自由和…...

2023-9-22 滑雪
题目链接:滑雪 #include <cstring> #include <algorithm> #include <iostream>using namespace std;const int N 310;int n, m; int h[N][N]; int f[N][N];int dx[4] {-1, 0, 1, 0}, dy[4] {0, 1, 0, -1};int dp(int x, int y) {int &v f…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
