想要精通算法和SQL的成长之路 - 最长等差数列
想要精通算法和SQL的成长之路 - 最长等差数列
- 前言
- 一. 最长等差数列
前言
想要精通算法和SQL的成长之路 - 系列导航
一. 最长等差数列
原题链接


思路:
- 我们假设
dp[i][j]为:以num[i]为结尾,以j为公差的最长等差子序列的长度。由此可知,我们的代码存在2个循环。 - 外层循环,针对
nums的每一个元素(下标为i),将其视为最长等差子序列的结尾元素。 - 内层循环,针对
[0,i)这个范围的元素,求得每种公差的最长等差子序列长度。此时二层循环下标索引为k,计算出每个元素和当前num[i]之间的公差:j。 - 即有:
dp[i][j] = Max(dp[i][j], dp[k][j] + 1)。 - 同时我们用一个全局变量res,不断地更新它的最大值即可。
res = Math.max(res, dp[i][j]);
注意的点:
- 考虑到公差为负数的情况,那么结合题目本身,我们可以发现公差的范围是
[-500,500],为了避免下标越界,我们统一把公差的值转为正数。即公差统一加上500,那么范围是[0,1000]。我们就可以初始化动态规划数组:int[][] dp = new int[nums.length][1001]; - 如果我们没有给数组的所有可能初始化为1(单个元素自身也可成为一个子数组,长度为1),我们只需要返回结果+1即可。
最终代码如下:
public class Test1027 {public int longestArithSeqLength(int[] nums) {int res = Integer.MIN_VALUE;int[][] dp = new int[nums.length][1001];for (int i = 1; i < nums.length; i++) {for (int k = 0; k < i; k++) {// 公差统一+500int j = nums[i] - nums[k] + 500;// 更新[0,i) 中,所有以 j 为公差 的最长子序列长度,同时更新dp[i][j]dp[i][j] = Math.max(dp[i][j], dp[k][j] + 1);// 更新最大值res = Math.max(res, dp[i][j]);}}return res + 1;}
}
相关文章:

想要精通算法和SQL的成长之路 - 最长等差数列
想要精通算法和SQL的成长之路 - 最长等差数列 前言一. 最长等差数列 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 最长等差数列 原题链接 思路: 我们假设dp[i][j] 为:以num[i]为结尾,以j为公差的最长等差子序列的长度。由此可知&a…...

【简单的自动曝光】python实现-附ChatGPT解析
1.题目 一个图像有 n 个像素点,存储在一个长度为 n 的数组 img 里, 每个像素点的取值范围[0,255] 的正整数。 请你给图像每个像素点值,加上一个整数 k (可以是负数),得到新图 newImg , 使得新图newImg 的所有像素平均值最接近中位值 128。 请输出这个整数 k。 输入描述 n …...

网工内推 | 运维工程师,CCNP认证优先,周末双休,多次调薪机会
01 驻场运维 职责描述: 1、驻场某大型汽车整车厂,配合客户完成网络相关(路由交换)的项目。 2、按照客户要求,与项目组配合共同完成项目前期调研,设计,规划,项目中期调试测试&#…...

LeetCode 1337. The K Weakest Rows in a Matrix【数组,二分,堆,快速选择,排序】1224
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

如何使用Spring提供的Retry
0、本例中使用的是 springboot-2.0.4.RELEASE,jdk1.8 1、导包。需要注意版本。2.0.0需要spring6和jdk17 <dependency><groupId>org.springframework.retry</groupId><artifactId>spring-retry</artifactId><version>1.3.4<…...
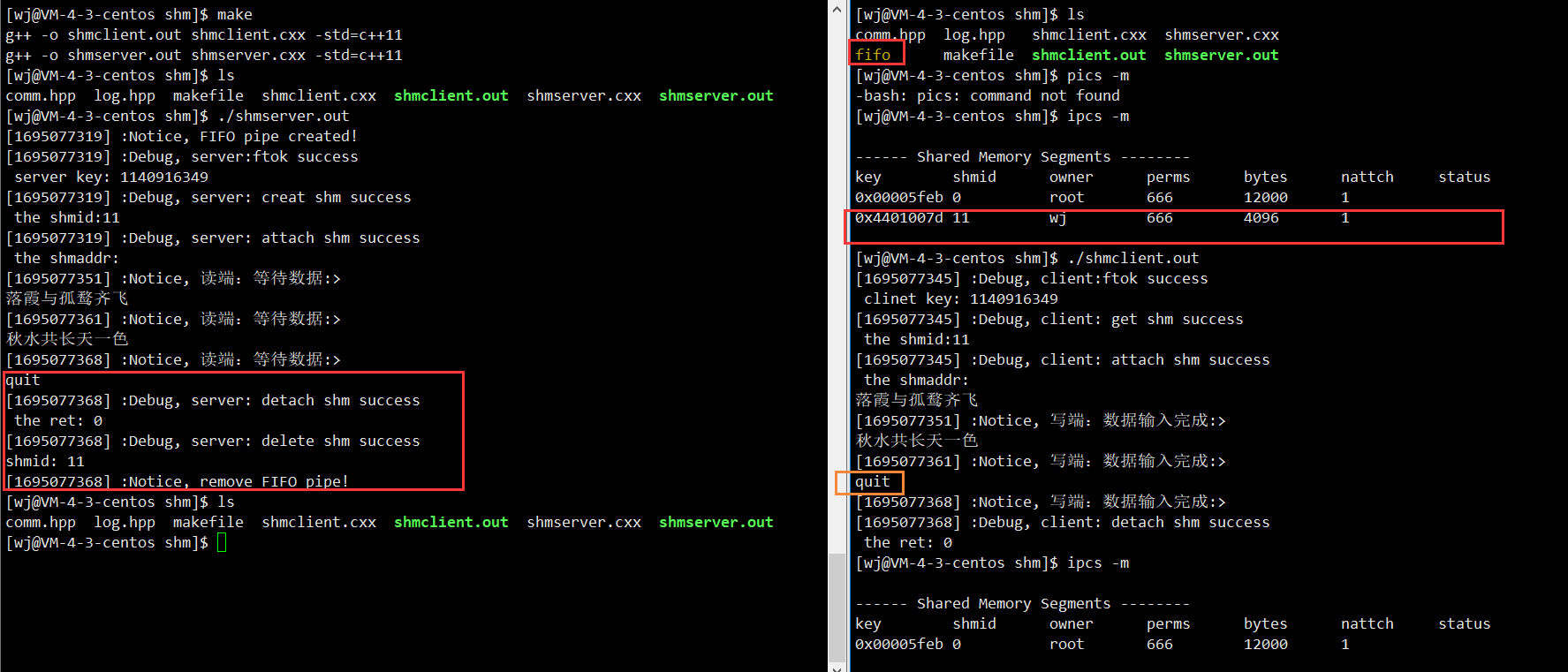
【ONE·Linux || 进程间通信】
总言 进程间通信:简述进程间通信,介绍一些通信方式,管道通信(匿名、名命)、共享内存等。 文章目录 总言1、进程间通信简述2、管道2.1、简介2.2、匿名管道2.2.1、匿名管道的原理2.2.2、编码理解:用fork来共…...
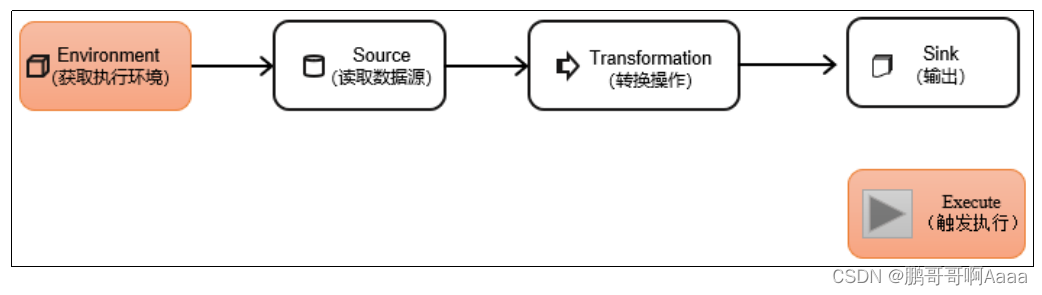
207.Flink(二):架构及核心概念,flink从各种数据源读取数据,各种算子转化数据,将数据推送到各数据源
一、Flink架构及核心概念 1.系统架构 JobMaster是JobManager中最核心的组件,负责处理单独的作业(Job)。一个job对应一个jobManager 2.并行度 (1)并行度(Parallelism)概念 一个特定算子的子任务(subtask)的个数被称之为其并行度(parallelism)。这样,包含并行子任…...
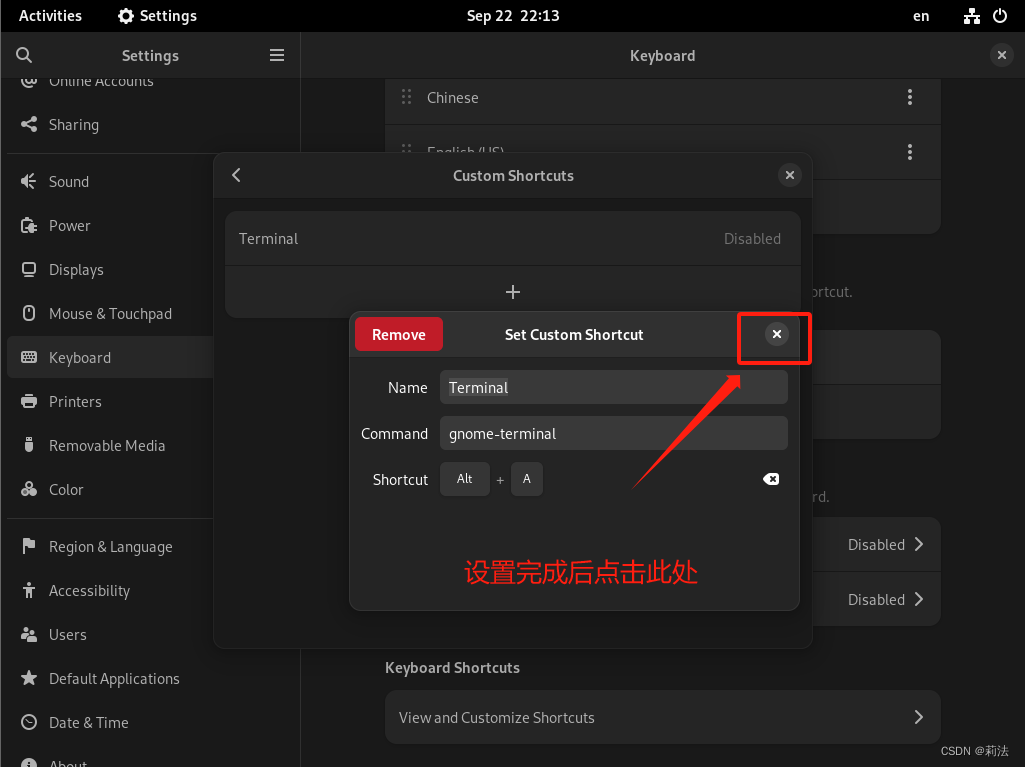
debian终端快捷键设置
为了方便使用图形化debian,快捷调出shell终端是提升工作学习效率的最重要的一步。 1.首先点击右上角,选择设置 2.点击键盘,选择快捷键,并创建自定义快捷键 3.点击添加快捷键 4.根据图中提示创建快捷键 Name: Terminal Command…...

原生ajax
什么是Ajax Asynchronous JavaScript and xml 异步的 js 和 xml(数据承载方式) ,本质:使用js提供的异步对象XMLHttpRequest 异步的向服务器提交请求,并且接受服务器响应回来的数据。 使用ajax 1.创建异步对象 var xhrnew XMLHttp…...
:并发编程)
面试题库(五):并发编程
多线程类的使用 java线程同步有哪些方法、各自的优缺点synchronized 和ReentrantLock区别,可重入锁是什么?threadlocal有什么用Java中创建线程有几种方式?分别是? 当主线程执行结束后,子线程还会继续执行下去吗?JUC中有哪些常用的集合?(项目中用到的)CopyOnWriteArray…...

Android FileProvider笔记
一、FileProvider是什么 通过FileProvider.getUriForFile(NonNull Context context, NonNull String authority, NonNull File file)方法获得一个有临时权限的Uri给客户端用来访问本APP文件。 当然看FileProvider类的注释更加详细 二、代码示例 <providerandroid:name&q…...
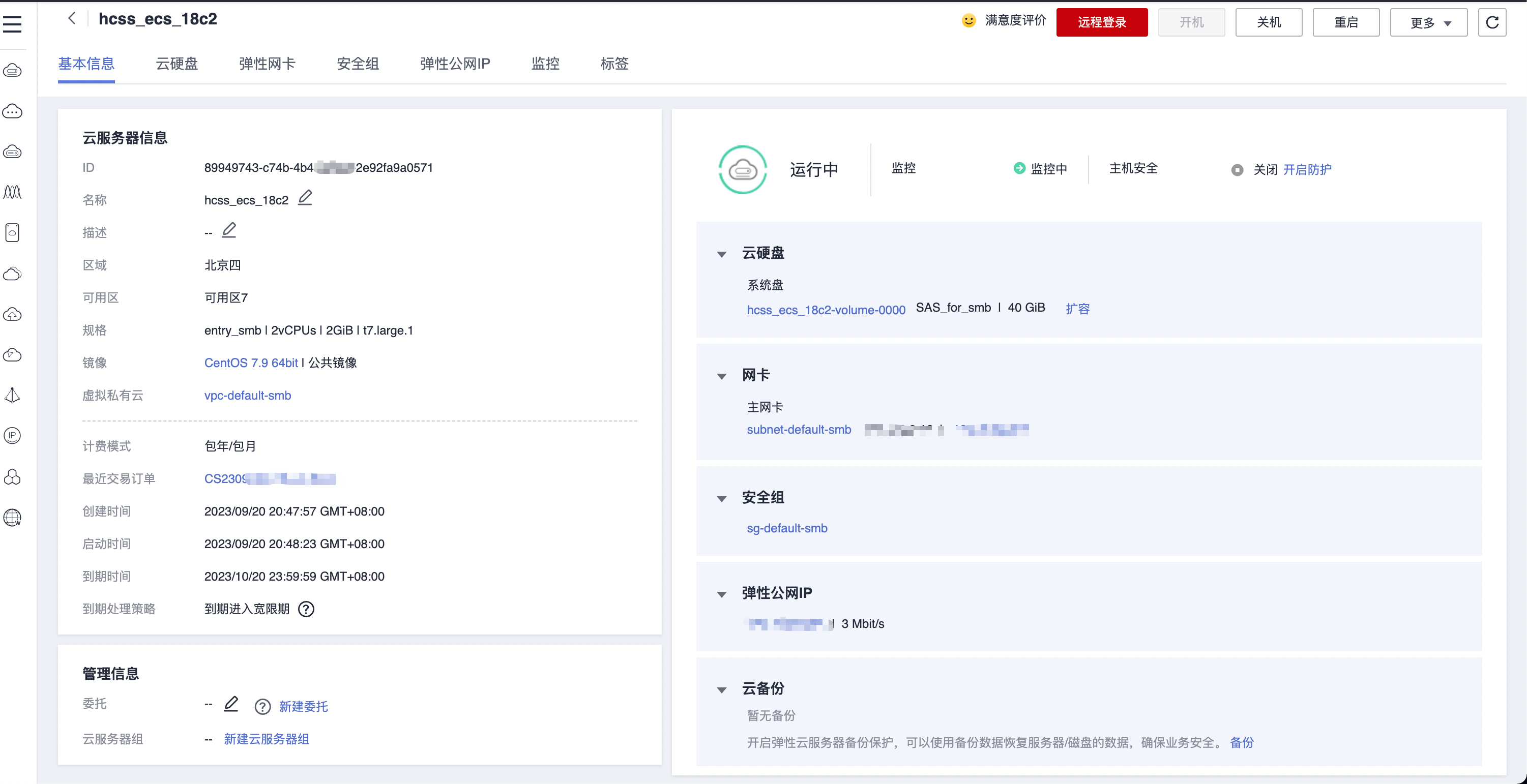
华为云云耀云服务器L实例评测 |云服务器选购
华为云耀云服务器 L 实例是一款轻量级云服务器,开通选择实例即可立刻使用,不需要用户再对服务器进行基础配置。新用户还有专享优惠,2 核心 2G 内存 3M 带宽的服务器只要 89 元/年,可以点击华为云云耀云服务器 L 实例购买地址去购买…...

2023-09-22 LeetCode每日一题(将钱分给最多的儿童)
2023-09-22每日一题 一、题目编号 2591. 将钱分给最多的儿童二、题目链接 点击跳转到题目位置 三、题目描述 给你一个整数 money ,表示你总共有的钱数(单位为美元)和另一个整数 children ,表示你要将钱分配给多少个儿童。 你…...

功能测试的重要性
前言 在软件开发领域,功能测试是确保软件质量的关键步骤之一。正如其名称所示,功能测试是验证软件产品是否具有其描述的功能和符合预期结果的过程。这种类型的测试非常重要,因为它不仅可以帮助团队检测潜在的缺陷并提高软件品质,…...

《Linux高性能服务器编程》--高级I/O函数
目录 1--Pipe() 2--dup() 和 dup2() 3--readv() 和 writev() 4--sendfile() 5--mmap() 和 munmap() 6--spice() 7--tea() 8--fcntl() 1--Pipe() #include <unistd.h> int pipe(int fd[2]); // 成功返回0,失败返回-1 pipe() 函数可用于创建一个管道&a…...
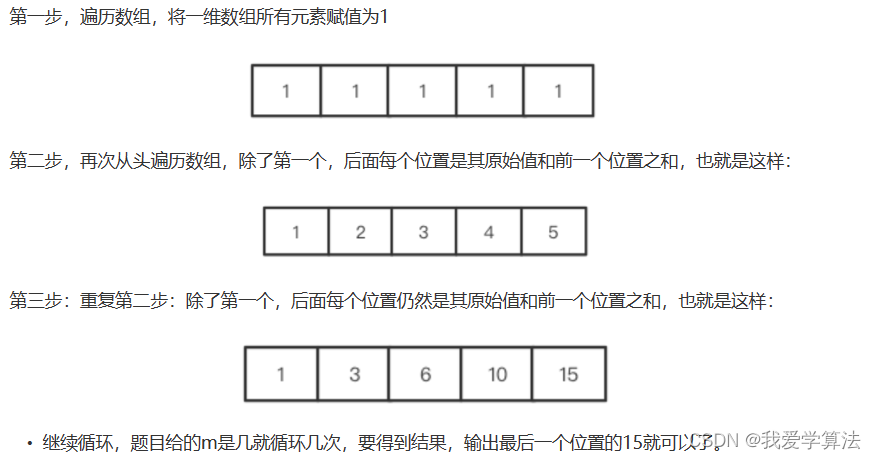
算法通关村 | 透彻理解动态规划
1. 斐波那契数列 1,1,2,3,5,8,13,..... f(n) f(n-1) f(n-2) 代码实现 public static int count_2 0;public int fibonacci(int n){if (n < 2){count_2;return n;}int f1 1;int f2 2;i…...
)
数据结构(持续更新)
嗯,怎么说数据结构果然很玄妙。按照能不能存储多行元素大致分为两类。 不能存好几行的数据包括pair,int,float,double,char,struct; 能存好几行的:map,unordered_map,list,vector,set,string,array。 1. pair “pair” 是 C++ 标准库中的一个模板类,它用于存储…...
nginx部署vue后显示500 Internal Server Error解决方案
前言 描述:当我配置好全部之后,通过 服务器 ip 地址访问,遇到报错信息:500 Internal Server Error。 今天部署vue前端项目一直报错500,无法显示出主页面。 一个以为是自己的dist位置没有访问正确或者nginx.conf的位…...

微调大型语言模型(一):为什么要微调(Why finetune)?
今天我们来学习Deeplearning.ai的在线课程 微调大型语言模型(一)的第一课:为什么要微调(Why finetune)。 我们知道像GPT-3.5这样的大型语言模型(LLM)它所学到的知识截止到2021年9月,那么如果我们向ChatGPT询问2022年以后发生的事情,它可能会…...

【GO】网络请求例子
post请求;multipart/form-data类型 // 构建请求参数requestData : map[string]interface{}{"gb": "","code": "","reMemberInfo": map[string]interface{}{"shi": "","…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
