数据结构--排序(1)
文章目录
- 排序概念
- 直接插入排序
- 希尔排序
- 冒泡排序
- 堆排序
- 选择排序
- 验证不同排序的运行时间
排序概念
排序指的是通过某一特征关键字(如信息量大小,首字母等)来对一连串的数据进行重新排列的操作,实现递增或者递减的数据排序。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
在实际的应用中是非常常见的。
文件的排序
购物的商品排序
在我们常见的排序算法中,有这几种:
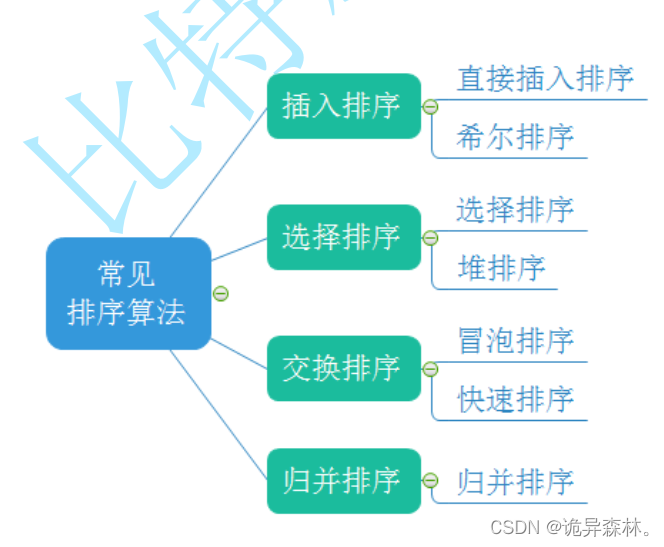
这些排序算法都是通过自身空间,通过不断交换来实现排序的。
直接插入排序
思想:当我们拿到了一组数组时,先将第一个元素定为前序序列,让第二个元素与它对比,以升序为例,大的就放在第一个元素之后,小的就放在第一个元素之前,放完之后,两个元素将成为新的前序序列;接着就是将第三个元素与前序序列的元素比较,比较最大的元素,也就是前序序列的最后一个元素,比它大就将元素向后挪移,为插入数腾出一个元素空间;依此类推。
玩斗地主时从小排到大的就是这种思想:
#include"Sort.h"
void PrintfArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}//直接插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){//将数组看作是一个个数插入进去的,从第二个数开始插入//比较插入数和前序序列最后一个数的大小//不符合条件就前序序列缩短,一直比较到大于end值停下来if (a[end] >tmp ){a[end + 1] = a[end];}else{break;}end--;}a[end + 1] = tmp;}}
内循环就是将新插入的数找到合适位置,让出空间,让新的数插入;
时间复杂度:O(N^2)
验证:
void TestInsertSort()
{int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 };InsertSort(a, sizeof(a) / sizeof(a[0]));PrintfArray(a, sizeof(a) / sizeof(a[0]));
}int main()
{TestInsertSort();return 0;
}
希尔排序
在上面的直接插入排序中,如果插入数一直大于前序序列,会发现内循环会走的比较快;因为都排序好了,只需要比较前序序列的最后一个元素即可;
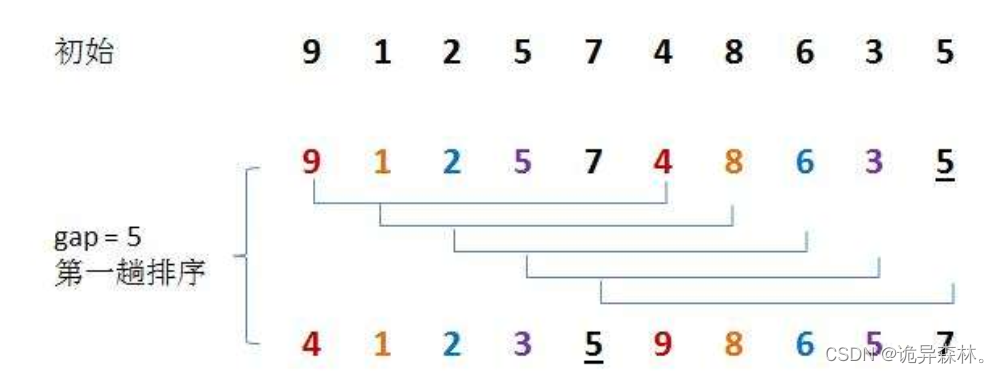
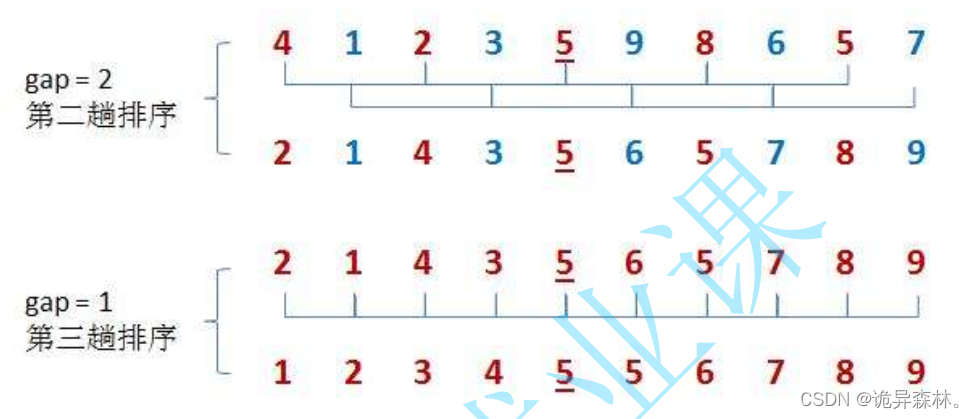
思想:希尔排序中,就是先将一组数组分成几等份,将每一份都进行排序,这样对于下次进行直接插入排序就预先做好了排序,简称预排序;接着不断缩短每一份的长度,一直做着预排序,直到每一份的长度为1时,就相当于上面的直接插入排序。
希尔排序就是对直接插入排序进行优化,通过预排序,让数组的排序比较有序,这样在再次排序时,就会省出会很多时间。
对于gap的取值,一般习惯直接对半取,但现在也有将gap取成三等份的;但实际效果都差不多;
void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}//希尔排序
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){//gap=gap/2;gap = gap/3 + 1;for (int i=0; i< n - gap; i ++){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
1.将tmp与前序序列相比大小,交换,最后将空出的位插入tmp;
2.前序序列扩大了,新增一个数;
3.在不同组中进行直插;
4.进行不断的预排序;
在这里,不是将每一组排完再进行下一组的排序,而是排一组的前序序列之后,跳掉下一组去进行排序到前序序列;gap若取3等份,要加上1,不然可能会出现达不到gap==1的情况,如为8时,gap取到2就停止了;
这里不要看着有很多层循环进行嵌套,实际上它的算法效率是远远高于直接插入排序的,以gap一直取二等份为例,1000个数据也就取10次gap,100万数据也就取20次gap,10亿才取24次gap,所以外层的循环实际次数是不大的,相对如此大的数据几乎可以忽略不计;
验证:
void TestShellSort()
{int a[]= { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 }; ShellSort(a, sizeof(a)/sizeof(a[0]));PrintfArray(a, sizeof(a) / sizeof(a[0]));
}
int main()
{TestShellSort();return 0;
}
时间复杂度:O(N^1.25) ~ O(1.6*N^1.25)
冒泡排序
思想:通过循环,不断的比较相邻的两个值,将最大的值往后放到最后一个位置,再通过一层循环,进行多躺的比较,总是将最大数往后放即可;
这样最大的数就排好了,以此类推排其他的数字;
//冒泡排序
void BubbleSort(int* a, int n)
{int mark = 0;for (int i = 0; i < n - 1; i++){for (int j = 0; j < n -1- i; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);mark = 0;}else{mark = 1;}}//表示没有进行交换,已排序好了if (mark == 1){break;}}}
时间复杂度:O(N^2)
堆排序
堆排序链接处
堆排序之前写过了,这里就不多解释;
void AdjustDown(int* a, int n, int parent)
{//左孩子int child = parent * 2 + 1;while (child<n){//右孩子比左孩子大if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
//堆排序
void HeapSort(int* a, int n)
{//建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}//交换int end = n - 1;while (end>0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
时间复杂度:O(N*logN)
选择排序
思想:在数组中找出最大值和最小值的下标,记录它,然后分别与起始与结尾位置进行交换,这样一次就能找出最大值和最小值了,接着缩短数组起始和结尾位置,然后再通过循环依次进行此步骤;
void SelectSort(int* a,int n)
{int begin = 0;int end = n - 1;while (begin < end){int min = begin;int max = begin;//找出区间里的max和minfor (int i = begin + 1; i <= end; i++){if (a[i] < a[min]){min = i;}if (a[i] > a[max]){max = i;}}//将最小数放在起始位置Swap(&a[begin], &a[min]);//max位置的数一旦被改变,max也需跟随改变if (max == begin){max = min;}Swap(&a[end], &a[max]);begin++;end--;}
}
这里需要注意的是,如果起始点就是最大数时,当最小数与起始位置交换后,那么max表示下标,max不变,仍然指着起始位置的下标,所以需要跟随max的值改变而改变;
O(N^2)
验证不同排序的运行时间
通过10000个数据来验证它们的排序运行时间;
void TestOP()
{srand(time(NULL));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);//赋值for (int i = 0; i < N; i++){a1[i] = rand();a2[i] = a1[i];a3[i] = a2[i];a4[i] = a3[i];a5[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();BubbleSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();SelectSort(a5, N);int end5 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("BubbleSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("SelectSort:%d\n", end5 - begin5);}
int main()
{TestOP();return 0;
}

相关文章:

数据结构--排序(1)
文章目录 排序概念直接插入排序希尔排序冒泡排序堆排序选择排序验证不同排序的运行时间 排序概念 排序指的是通过某一特征关键字(如信息量大小,首字母等)来对一连串的数据进行重新排列的操作,实现递增或者递减的数据排序。 稳定…...

【AI视野·今日NLP 自然语言处理论文速览 第三十七期】Thu, 21 Sep 2023
AI视野今日CS.NLP 自然语言处理论文速览 Thu, 21 Sep 2023 Totally 57 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers Chain-of-Verification Reduces Hallucination in Large Language Models Authors Shehzaad Dhuliawala, Mojt…...

高防服务器防护效果怎么样?
对于很多拥有在线业务的公司,数据是非常重要,如果遭到网络攻击会导致很严重的后果,所以很多公司选择高防服务器,那么高防服务器防护效果是怎么样的呢?今天就让小编带大家看一看吧! 弹性带宽。高防服务器一…...

tomcat架构概览
https://blog.csdn.net/ldw201510803006/article/details/119880100 前言 Tomcat 要实现 2 个核心功能: 处理 Socket 连接,负责网络字节流与 Request 和 Response 对象的转化。加载和管理 Servlet,以及具体处理 Request 请求。 因此 Tomc…...

海康的资料
系列文章目录 文章目录 系列文章目录前言一、海康二、使用步骤1.引入库2.读入数据 总结 前言 提示:这里可以添加本文要记录的大概内容: 例如:随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学…...

【ELFK】之消息队列kafka
本章结构: 1、为什么要使用消息队列MQ 2、使用消息队列的好处 3、消息队列的两种模式 4、对Kafka的概述 5、Kafka的特性 6、Kafka的系统架构 7、部署Kafka Kafka 定义 Kafka 是一个分布式的基于发布/订阅模式的消息队列(MQ,Message Qu…...
Qt核心:元对象系统、属性系统、对象树、信号槽
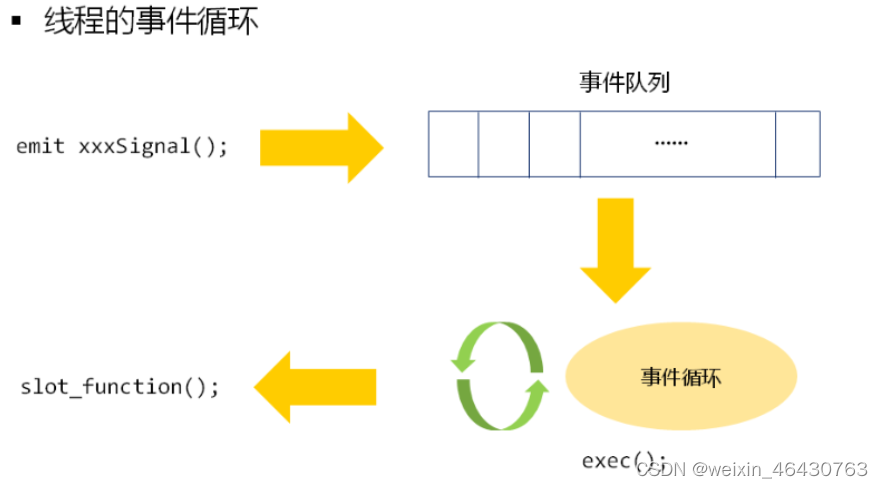
一、元对象系统 1、Qt 的元对象系统提供的功能有:对象间通信的信号和槽机制、运行时类型信息和动态属性系统等。 2、元对象系统是 Qt 对原有的 C进行的一些扩展,主要是为实现信号和槽机制而引入的, 信号和槽机制是 Qt 的核心特征。 3、要使…...
【若依框架2】前后端分离版本添加功能页
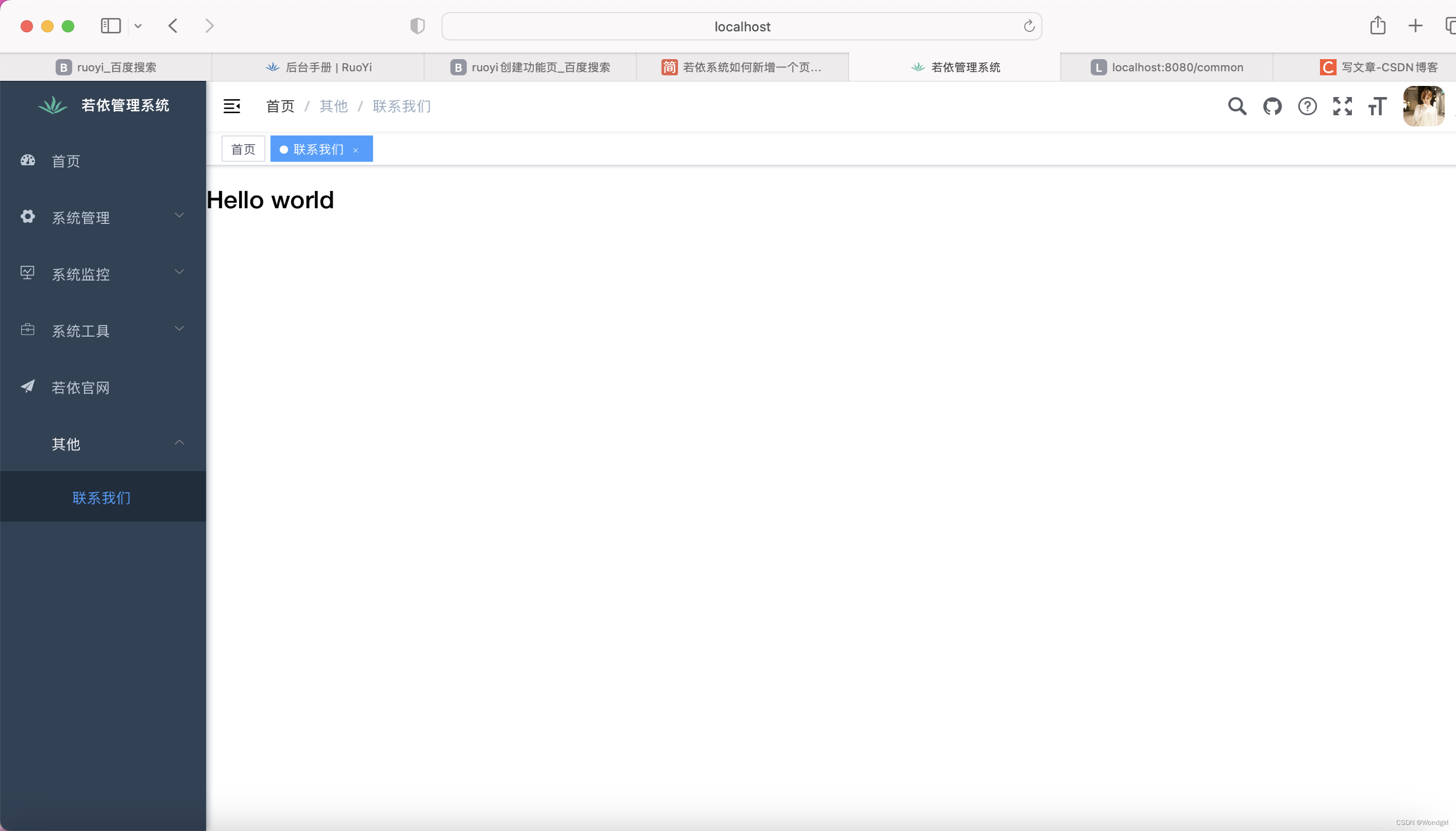
在VSCode的src/views下新建个文件平example,在example下创建test文件夹,在test里创建index.vue文件 <template> <h1>Hello world</h1> </template><script> export default {name: "index" } </script><style s…...
Unity Bolt模块间通信
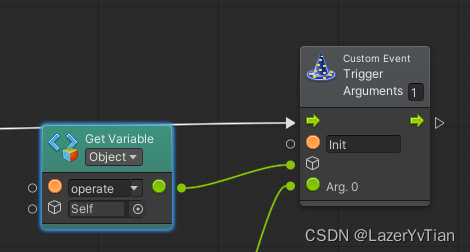
使用Bolt无代码设计开发的时候,我们不能简单的认为只需要一个FlowMachine就可以完成所有流程的开发。我们需要不同的模块进行拆分,以便更好的管理和协作。这就需要不同模块之间的通信处理。经过研究与使用,将常用的通信方式总结如下ÿ…...
please choose a certificate and try again.(-5)报错怎么解决
the server you want to connect to requests identification,please choose a certificate and try again.(-5)...

国产自研BI系统,更懂中国企业数据分析需求
国产自研BI系统是指由中国企业自主研发的商业智能(BI)系统,这类系统更加了解中国企业的数据分析需求,能够提供更加贴合实际的解决方案。比如说奥威BI系统就是典型的国产自研,不仅了解中国企业的数据分析需求࿰…...
基于Java的高校竞赛管理系统设计与实现(亮点:发起比赛、报名、审核、评委打分、获奖排名,可随意更换主题如蓝桥杯、ACM、王者荣耀、吃鸡等竞赛)
高校竞赛管理系统 一、前言二、我的优势2.1 自己的网站2.2 自己的小程序(小蔡coding)2.3 有保障的售后2.4 福利 三、开发环境与技术3.1 MySQL数据库3.2 Vue前端技术3.3 Spring Boot框架3.4 微信小程序 四、功能设计4.1 主要功能描述4.2 系统角色 五、系统…...

出血性脑卒中临床智能诊疗建模
先说下数据,随访流水号是患者的后续诊断号码,表3有对应的数据,首先需要做下数据整理,需要整理出每次诊断的指标(包括表1中人物信息、表2中的检查指标以及表3中的检查指标,表4中有对应的时间,以刚…...
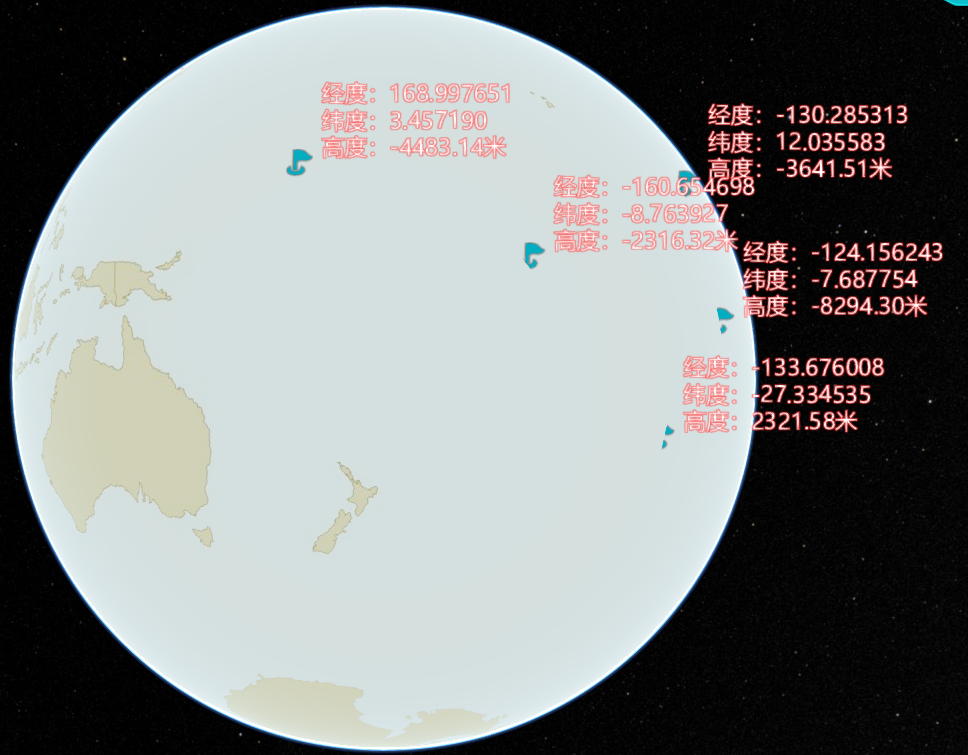
Cesium 空间量算——生成点位坐标
文章目录 需求分析1. 点击坐标点实现2. 输入坐标实现 需求 用 Cesium 生成点位坐标,并明显标识 分析 以下是我的两种实现方式 第一种是坐标点击实现 第二种是输入坐标实现 1. 点击坐标点实现 //点位坐标getLocation() {this.hoverIndex 0;let that this;this.view…...

为什么曲面函数的偏导数可以表示其曲面的法向量?
为什么曲面函数的偏导数可以表示其曲面的法向量? 引用资料: 1.知乎shinbade:曲面的三个偏导数为什么能表示法向量? 2.Geogebra羅驥韡 (Pegasus Roe):偏導數、切平面、梯度 曲面 F ( x , y , z ) 0 F(x,y,z)0 F(x,y,…...

❤Uniapp报npx update-browserslist-db@latest
❤ Uniapp报npx update-browserslist-dblatest 按照提示先更新一下 npx update-browserslist-dblatest然后打开一下端口...
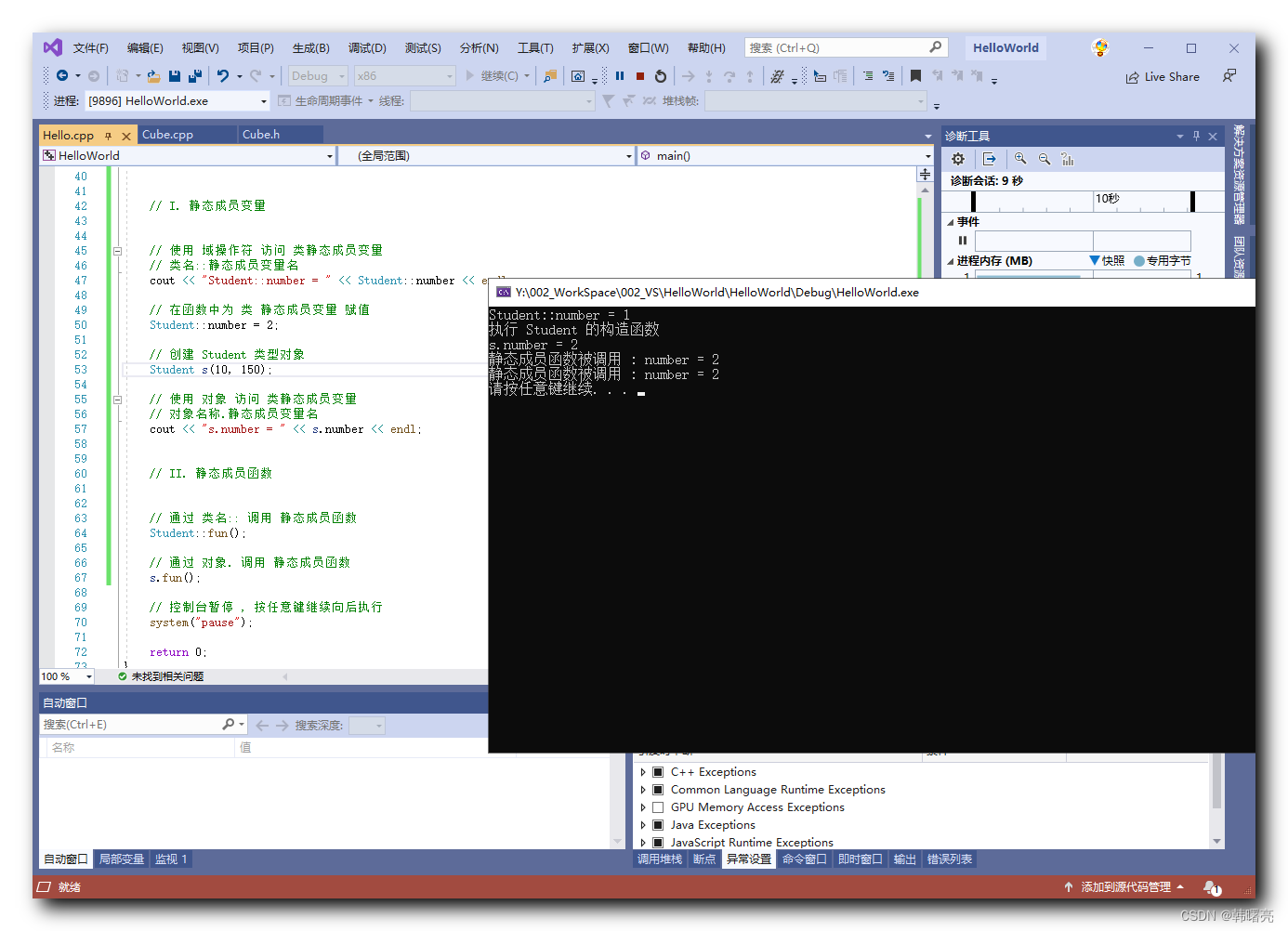
【C++】静态成员函数 ( 静态成员函数概念 | 静态成员函数声明 | 静态成员函数访问 | 静态成员函数只能访问静态成员 )
文章目录 一、静态成员函数简介1、静态成员函数概念2、静态成员函数声明3、静态成员函数访问4、静态成员函数只能访问静态成员 二、代码示例 - 静态成员函数 一、静态成员函数简介 1、静态成员函数概念 静态成员函数归属 : 在 C 类中 , 静态成员函数 是一种 特殊的函数 , 该函数…...
)
基于若依ruoyi-nbcio增加flowable流程待办消息的提醒,并提供右上角的红字数字提醒(三)
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 1、上一节说到RedisReceiver ,这里有调用了NbcioRedisListener自定义业务监听,如下…...

用友第五届开发者大赛初赛晋级公示,复赛火热进行中!
用友第五届开发者大赛初赛晋级公示,复赛火热进行中! 自7月13日鸣锣揭幕,9月6日各赛道作品初评工作完成,历时近两月,用友第五届企业云服务开发者大赛初赛阶段顺利落下帷幕。作为备受各界开发者关注的赛事,本…...

SSL证书如何做到保障网站安全?
当网站显示不安全时,用户会在头脑中产生该网站是否合法的疑问,如果是购物网站或者购物商城,那意味着可能会损失大部分的用户。而SSL证书能有效保障网站的安全性,轻松解决网站不被用户信任的问题。那么,SSL证书究竟是如…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...