为什么曲面函数的偏导数可以表示其曲面的法向量?
为什么曲面函数的偏导数可以表示其曲面的法向量?
引用资料:
1.知乎@shinbade:曲面的三个偏导数为什么能表示法向量?
2.Geogebra@羅驥韡 (Pegasus Roe):偏導數、切平面、梯度
曲面 F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0,曲面上一点A ( x , y , z ) (x,y,z) (x,y,z),在该点附近取另一点B ( x + Δ x , y + Δ y , z + Δ z ) (x+\Delta x,y+\Delta y,z+\Delta z) (x+Δx,y+Δy,z+Δz),由于点B也在曲面上,故 F ( x + Δ x , y + Δ y , z + Δ z ) = 0 F(x+\Delta x,y+\Delta y,z+\Delta z)=0 F(x+Δx,y+Δy,z+Δz)=0,
将上式进行一阶泰勒展开:(一阶展开目的是用切平面上的点近似曲面上的点)
F ( x + Δ x , y + Δ y , z + Δ z ) = F ( x , y , z ) + F x ′ Δ x + F y ′ Δ y + F z ′ Δ z = 0 ∵ F ( x , y , z ) = 0 ∴ F x ′ Δ x + F y ′ Δ y + F z ′ Δ z = 0 ( F x ′ , F y ′ , F z ′ ) ⋅ ( Δ x , Δ y , Δ z ) = 0 F(x+\Delta x,y+\Delta y,z+\Delta z)=F(x,y,z)+F'_x\Delta x+F'_y\Delta y+F'_z\Delta z=0\\ ~\\ \because F(x,y,z)=0\\ ~\\ \therefore F'_x\Delta x+F'_y\Delta y+F'_z\Delta z=0\\ ~\\ (F'_x,F'_y,F'_z)\cdot(\Delta x,\Delta y,\Delta z)=0 F(x+Δx,y+Δy,z+Δz)=F(x,y,z)+Fx′Δx+Fy′Δy+Fz′Δz=0 ∵F(x,y,z)=0 ∴Fx′Δx+Fy′Δy+Fz′Δz=0 (Fx′,Fy′,Fz′)⋅(Δx,Δy,Δz)=0
向量 ( Δ x , Δ y , Δ z ) (\Delta x,\Delta y,\Delta z) (Δx,Δy,Δz)与向量 ( F x ′ , F y ′ , F z ′ ) (F'_x,F'_y,F'_z) (Fx′,Fy′,Fz′)内积为0,说明两向量垂直,又由于向量 ( Δ x , Δ y , Δ z ) (\Delta x,\Delta y,\Delta z) (Δx,Δy,Δz)在切平面上(严格来说是割平面,因为还没有取极限),故向量 ( F x ′ , F y ′ , F z ′ ) (F'_x,F'_y,F'_z) (Fx′,Fy′,Fz′)垂直于切平面,也就可以用其来表示曲面的法向量。
备注:切平面上点代替曲面上点(以直代曲),这个方面的理解详见本人博客:如何理解二元函数的可导与可微?
由于在极限过程中,切平面上点无限接近曲面上的点,所以近似将向量 ( Δ x , Δ y , Δ z ) (\Delta x,\Delta y,\Delta z) (Δx,Δy,Δz)看作在切片面上。




相关文章:

为什么曲面函数的偏导数可以表示其曲面的法向量?
为什么曲面函数的偏导数可以表示其曲面的法向量? 引用资料: 1.知乎shinbade:曲面的三个偏导数为什么能表示法向量? 2.Geogebra羅驥韡 (Pegasus Roe):偏導數、切平面、梯度 曲面 F ( x , y , z ) 0 F(x,y,z)0 F(x,y,…...

❤Uniapp报npx update-browserslist-db@latest
❤ Uniapp报npx update-browserslist-dblatest 按照提示先更新一下 npx update-browserslist-dblatest然后打开一下端口...
【C++】静态成员函数 ( 静态成员函数概念 | 静态成员函数声明 | 静态成员函数访问 | 静态成员函数只能访问静态成员 )
文章目录 一、静态成员函数简介1、静态成员函数概念2、静态成员函数声明3、静态成员函数访问4、静态成员函数只能访问静态成员 二、代码示例 - 静态成员函数 一、静态成员函数简介 1、静态成员函数概念 静态成员函数归属 : 在 C 类中 , 静态成员函数 是一种 特殊的函数 , 该函数…...
)
基于若依ruoyi-nbcio增加flowable流程待办消息的提醒,并提供右上角的红字数字提醒(三)
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 1、上一节说到RedisReceiver ,这里有调用了NbcioRedisListener自定义业务监听,如下…...

用友第五届开发者大赛初赛晋级公示,复赛火热进行中!
用友第五届开发者大赛初赛晋级公示,复赛火热进行中! 自7月13日鸣锣揭幕,9月6日各赛道作品初评工作完成,历时近两月,用友第五届企业云服务开发者大赛初赛阶段顺利落下帷幕。作为备受各界开发者关注的赛事,本…...

SSL证书如何做到保障网站安全?
当网站显示不安全时,用户会在头脑中产生该网站是否合法的疑问,如果是购物网站或者购物商城,那意味着可能会损失大部分的用户。而SSL证书能有效保障网站的安全性,轻松解决网站不被用户信任的问题。那么,SSL证书究竟是如…...
C# Onnx Yolov8 Detect Poker 扑克牌识别
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System…...

想要精通算法和SQL的成长之路 - 最长等差数列
想要精通算法和SQL的成长之路 - 最长等差数列 前言一. 最长等差数列 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 最长等差数列 原题链接 思路: 我们假设dp[i][j] 为:以num[i]为结尾,以j为公差的最长等差子序列的长度。由此可知&a…...

【简单的自动曝光】python实现-附ChatGPT解析
1.题目 一个图像有 n 个像素点,存储在一个长度为 n 的数组 img 里, 每个像素点的取值范围[0,255] 的正整数。 请你给图像每个像素点值,加上一个整数 k (可以是负数),得到新图 newImg , 使得新图newImg 的所有像素平均值最接近中位值 128。 请输出这个整数 k。 输入描述 n …...

网工内推 | 运维工程师,CCNP认证优先,周末双休,多次调薪机会
01 驻场运维 职责描述: 1、驻场某大型汽车整车厂,配合客户完成网络相关(路由交换)的项目。 2、按照客户要求,与项目组配合共同完成项目前期调研,设计,规划,项目中期调试测试&#…...

LeetCode 1337. The K Weakest Rows in a Matrix【数组,二分,堆,快速选择,排序】1224
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

如何使用Spring提供的Retry
0、本例中使用的是 springboot-2.0.4.RELEASE,jdk1.8 1、导包。需要注意版本。2.0.0需要spring6和jdk17 <dependency><groupId>org.springframework.retry</groupId><artifactId>spring-retry</artifactId><version>1.3.4<…...
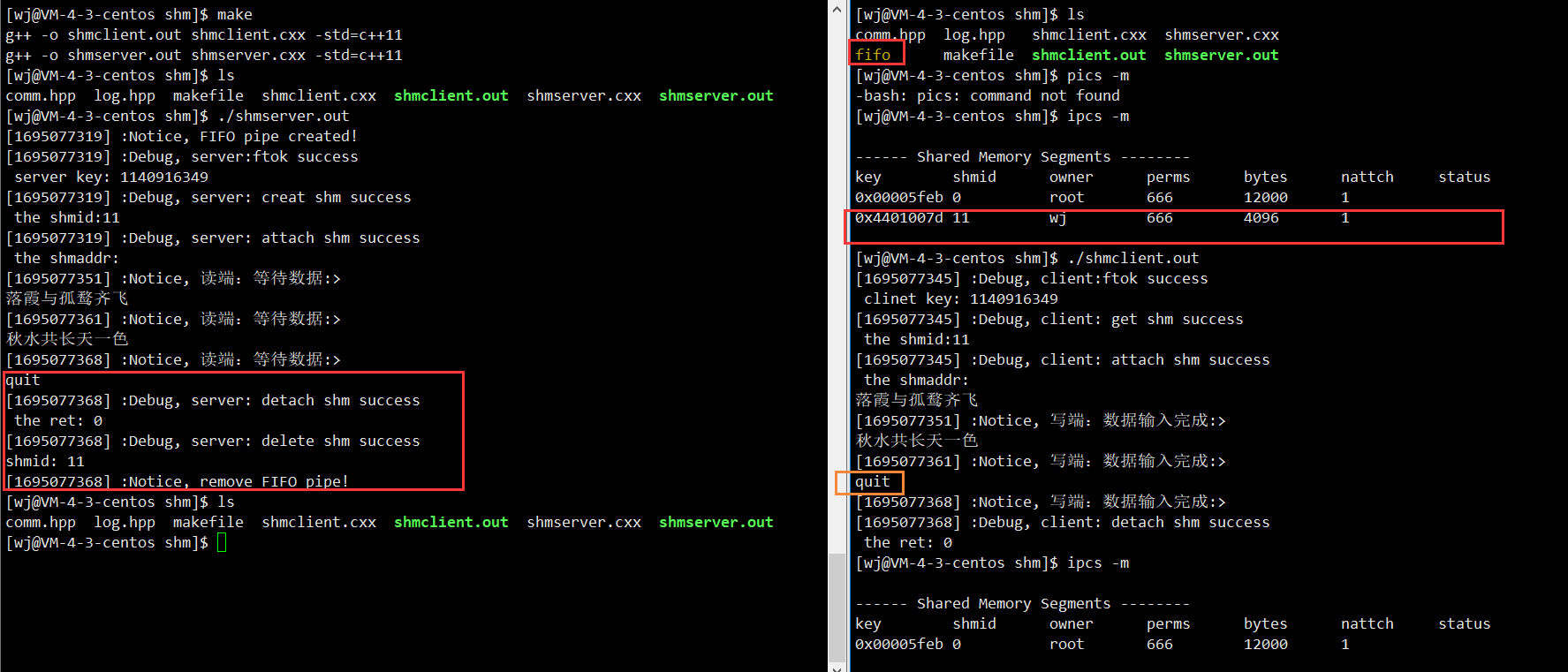
【ONE·Linux || 进程间通信】
总言 进程间通信:简述进程间通信,介绍一些通信方式,管道通信(匿名、名命)、共享内存等。 文章目录 总言1、进程间通信简述2、管道2.1、简介2.2、匿名管道2.2.1、匿名管道的原理2.2.2、编码理解:用fork来共…...
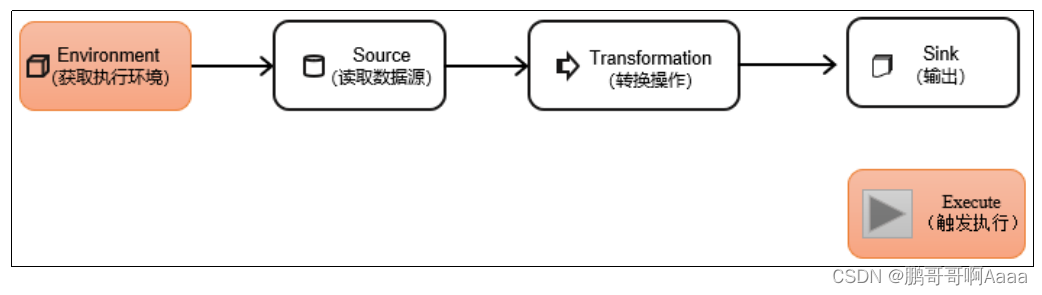
207.Flink(二):架构及核心概念,flink从各种数据源读取数据,各种算子转化数据,将数据推送到各数据源
一、Flink架构及核心概念 1.系统架构 JobMaster是JobManager中最核心的组件,负责处理单独的作业(Job)。一个job对应一个jobManager 2.并行度 (1)并行度(Parallelism)概念 一个特定算子的子任务(subtask)的个数被称之为其并行度(parallelism)。这样,包含并行子任…...
debian终端快捷键设置
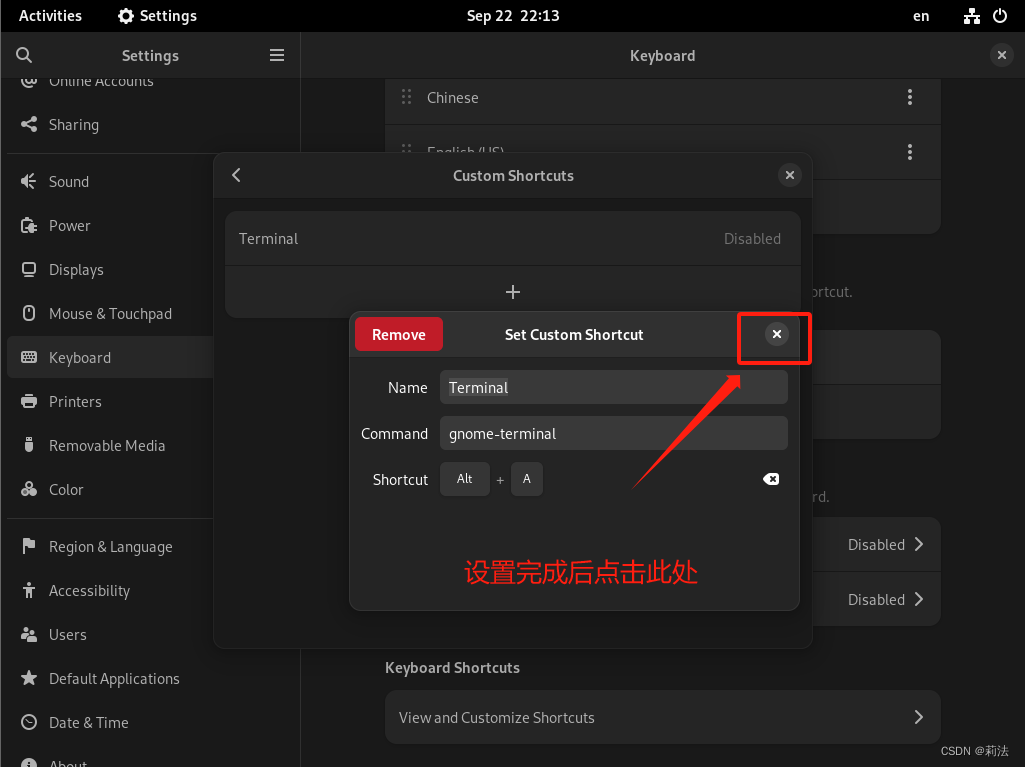
为了方便使用图形化debian,快捷调出shell终端是提升工作学习效率的最重要的一步。 1.首先点击右上角,选择设置 2.点击键盘,选择快捷键,并创建自定义快捷键 3.点击添加快捷键 4.根据图中提示创建快捷键 Name: Terminal Command…...

原生ajax
什么是Ajax Asynchronous JavaScript and xml 异步的 js 和 xml(数据承载方式) ,本质:使用js提供的异步对象XMLHttpRequest 异步的向服务器提交请求,并且接受服务器响应回来的数据。 使用ajax 1.创建异步对象 var xhrnew XMLHttp…...
:并发编程)
面试题库(五):并发编程
多线程类的使用 java线程同步有哪些方法、各自的优缺点synchronized 和ReentrantLock区别,可重入锁是什么?threadlocal有什么用Java中创建线程有几种方式?分别是? 当主线程执行结束后,子线程还会继续执行下去吗?JUC中有哪些常用的集合?(项目中用到的)CopyOnWriteArray…...

Android FileProvider笔记
一、FileProvider是什么 通过FileProvider.getUriForFile(NonNull Context context, NonNull String authority, NonNull File file)方法获得一个有临时权限的Uri给客户端用来访问本APP文件。 当然看FileProvider类的注释更加详细 二、代码示例 <providerandroid:name&q…...
华为云云耀云服务器L实例评测 |云服务器选购
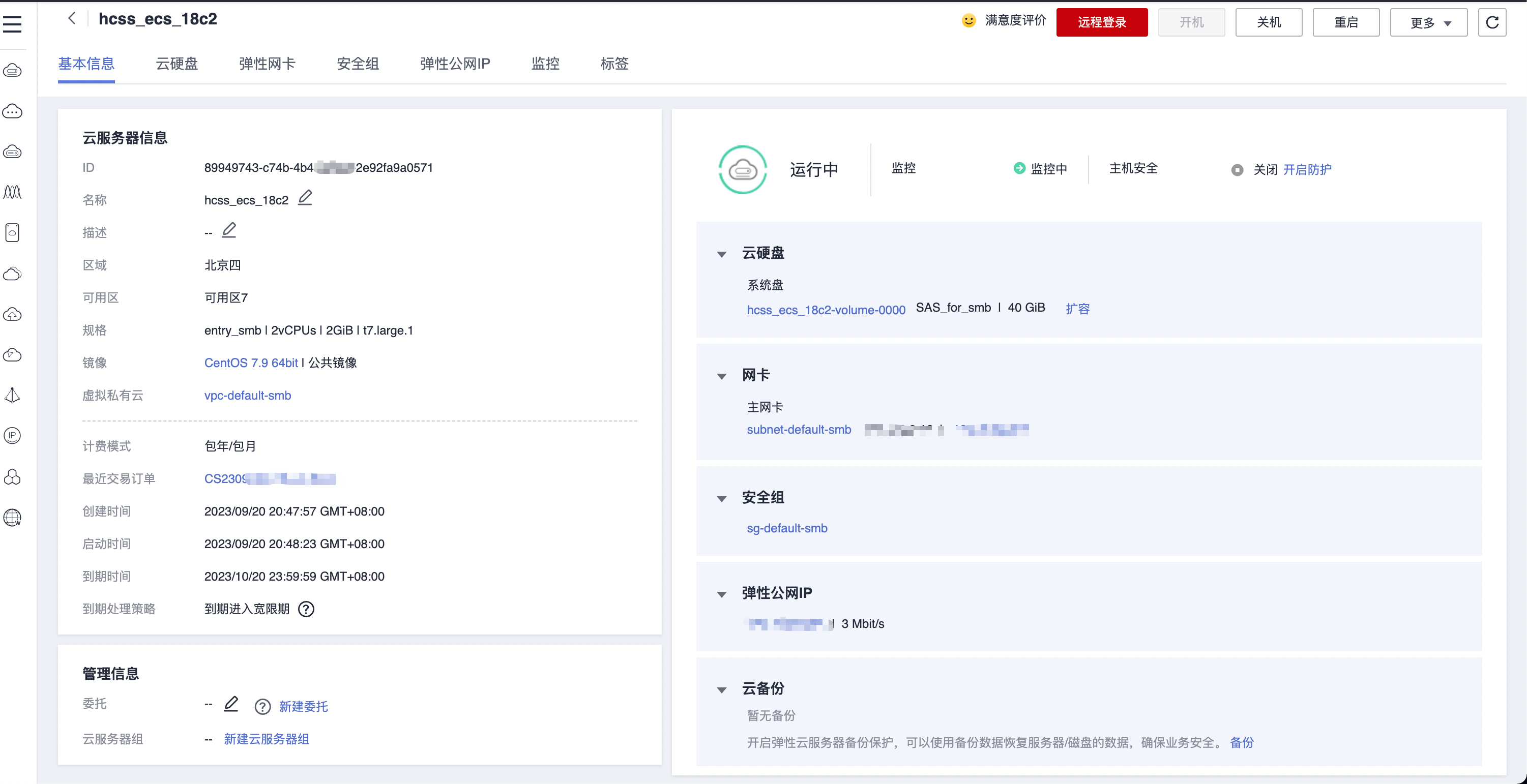
华为云耀云服务器 L 实例是一款轻量级云服务器,开通选择实例即可立刻使用,不需要用户再对服务器进行基础配置。新用户还有专享优惠,2 核心 2G 内存 3M 带宽的服务器只要 89 元/年,可以点击华为云云耀云服务器 L 实例购买地址去购买…...

2023-09-22 LeetCode每日一题(将钱分给最多的儿童)
2023-09-22每日一题 一、题目编号 2591. 将钱分给最多的儿童二、题目链接 点击跳转到题目位置 三、题目描述 给你一个整数 money ,表示你总共有的钱数(单位为美元)和另一个整数 children ,表示你要将钱分配给多少个儿童。 你…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
