国产自研BI系统,更懂中国企业数据分析需求
国产自研BI系统是指由中国企业自主研发的商业智能(BI)系统,这类系统更加了解中国企业的数据分析需求,能够提供更加贴合实际的解决方案。比如说奥威BI系统就是典型的国产自研,不仅了解中国企业的数据分析需求,还根据多年的经验为中国企业量身打造了多套标准化的BI数据分析解决方案,为中国企业提供更低风险、高效性、高性价比的智能数据分析决策服务。
1、国产自研BI系统更加熟悉中国企业的数据特点和使用习惯。
由于中国企业具有自身的业务特点和数据管理模式,因此,国产自研BI系统-奥威BI能够更好地适应这些特点,提供更加贴合实际的解决方案。例如,对于中国企业的财务报表分析,奥威BI系统可以更好地理解各种财务报表的格式和内容,提供更加准确的财务数据分析结果,甚至可以提供标准化的智能财务分析方案。

2、国产自研BI系统更加注重用户体验和操作便捷性。
由于中国企业对于商业智能系统的使用体验和操作便捷性有较高的要求,因此,奥威BI系统更加注重这些方面。例如,可以通过简单的拖拽和配置来实现复杂的数据分析,同时支持多种数据源的接入和管理,使得用户可以更加轻松地完成数据分析工作。
3、国产自研BI系统具有更高的自主可控性。
由于自主研发的奥威BI系统不受外部制约和限制,因此可以更好地满足企业的实际需求,并且可以更好地保障数据安全。例如,可以通过内置加密算法和权限控制机制来实现数据的安全保护,确保企业的商业机密和隐私不被泄露。
4、国产自研BI系统具有更好的适配性和可扩展性。
由于自主研发的奥威BI系统可以更好地适应企业的实际业务场景和未来发展需求,因此可以为企业提供更加贴合实际的解决方案。同时,国产自研的奥威BI系统也具有更好的可扩展性,可以支持更多的业务场景和应用。
作为一款国产自研BI系统,奥威BI系统更了解中国企业的数据分析需求,注重用户体验和操作便捷性,具有更高的自主可控性、更好的适配性和可扩展性。
相关文章:

国产自研BI系统,更懂中国企业数据分析需求
国产自研BI系统是指由中国企业自主研发的商业智能(BI)系统,这类系统更加了解中国企业的数据分析需求,能够提供更加贴合实际的解决方案。比如说奥威BI系统就是典型的国产自研,不仅了解中国企业的数据分析需求࿰…...
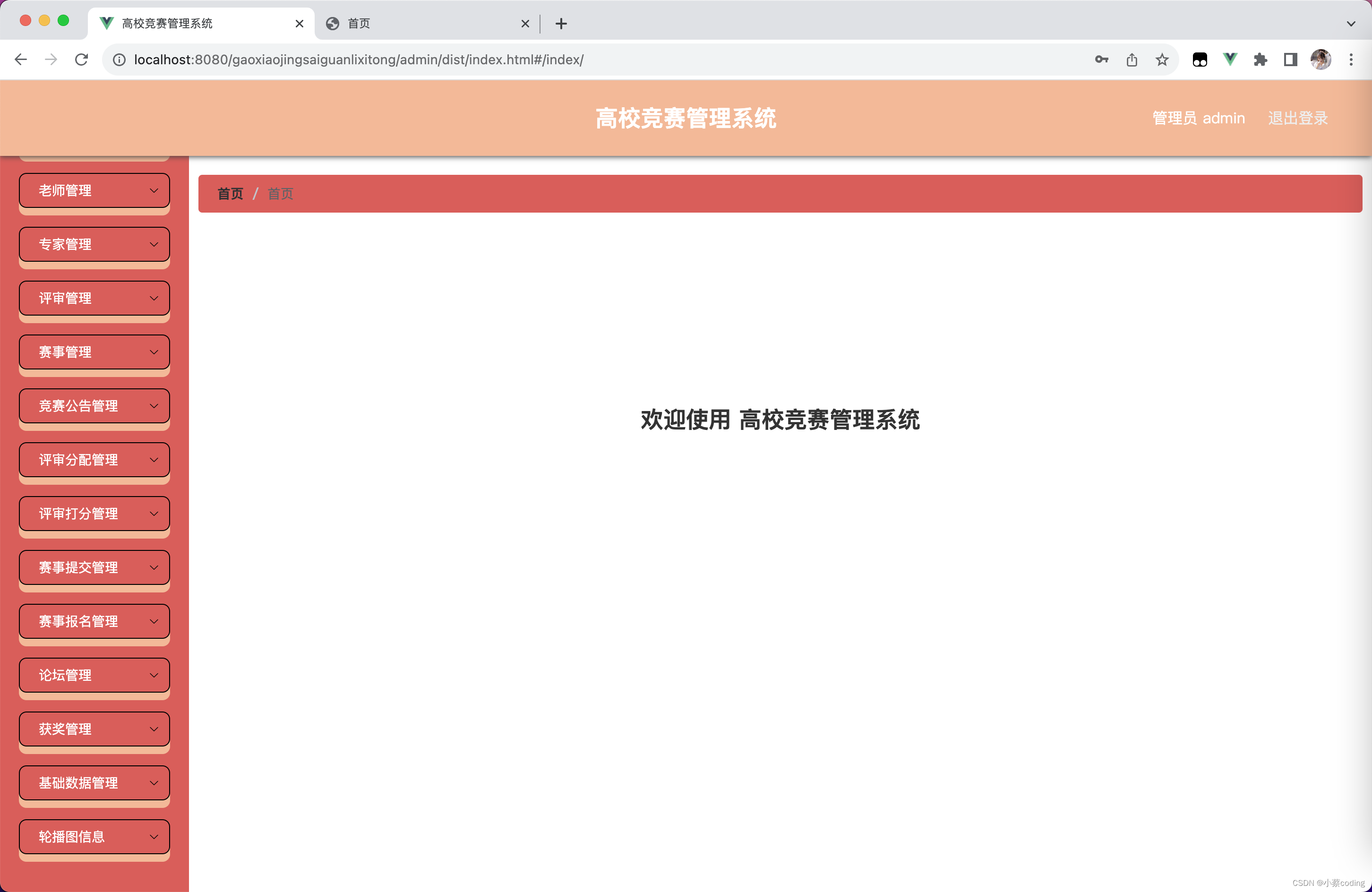
基于Java的高校竞赛管理系统设计与实现(亮点:发起比赛、报名、审核、评委打分、获奖排名,可随意更换主题如蓝桥杯、ACM、王者荣耀、吃鸡等竞赛)
高校竞赛管理系统 一、前言二、我的优势2.1 自己的网站2.2 自己的小程序(小蔡coding)2.3 有保障的售后2.4 福利 三、开发环境与技术3.1 MySQL数据库3.2 Vue前端技术3.3 Spring Boot框架3.4 微信小程序 四、功能设计4.1 主要功能描述4.2 系统角色 五、系统…...

出血性脑卒中临床智能诊疗建模
先说下数据,随访流水号是患者的后续诊断号码,表3有对应的数据,首先需要做下数据整理,需要整理出每次诊断的指标(包括表1中人物信息、表2中的检查指标以及表3中的检查指标,表4中有对应的时间,以刚…...
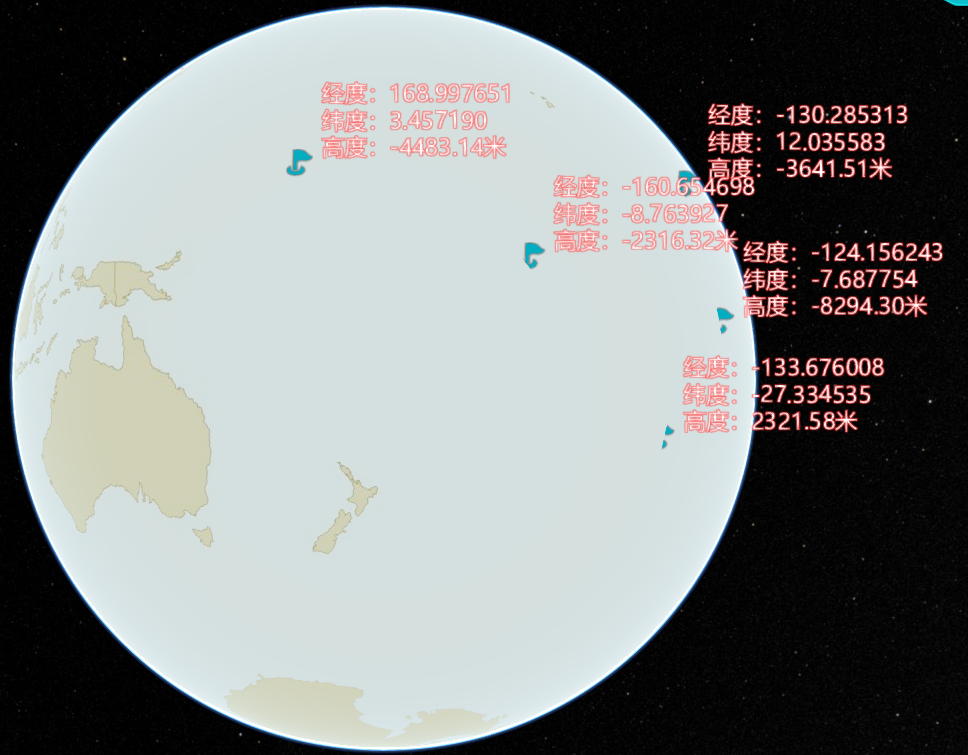
Cesium 空间量算——生成点位坐标
文章目录 需求分析1. 点击坐标点实现2. 输入坐标实现 需求 用 Cesium 生成点位坐标,并明显标识 分析 以下是我的两种实现方式 第一种是坐标点击实现 第二种是输入坐标实现 1. 点击坐标点实现 //点位坐标getLocation() {this.hoverIndex 0;let that this;this.view…...

为什么曲面函数的偏导数可以表示其曲面的法向量?
为什么曲面函数的偏导数可以表示其曲面的法向量? 引用资料: 1.知乎shinbade:曲面的三个偏导数为什么能表示法向量? 2.Geogebra羅驥韡 (Pegasus Roe):偏導數、切平面、梯度 曲面 F ( x , y , z ) 0 F(x,y,z)0 F(x,y,…...

❤Uniapp报npx update-browserslist-db@latest
❤ Uniapp报npx update-browserslist-dblatest 按照提示先更新一下 npx update-browserslist-dblatest然后打开一下端口...
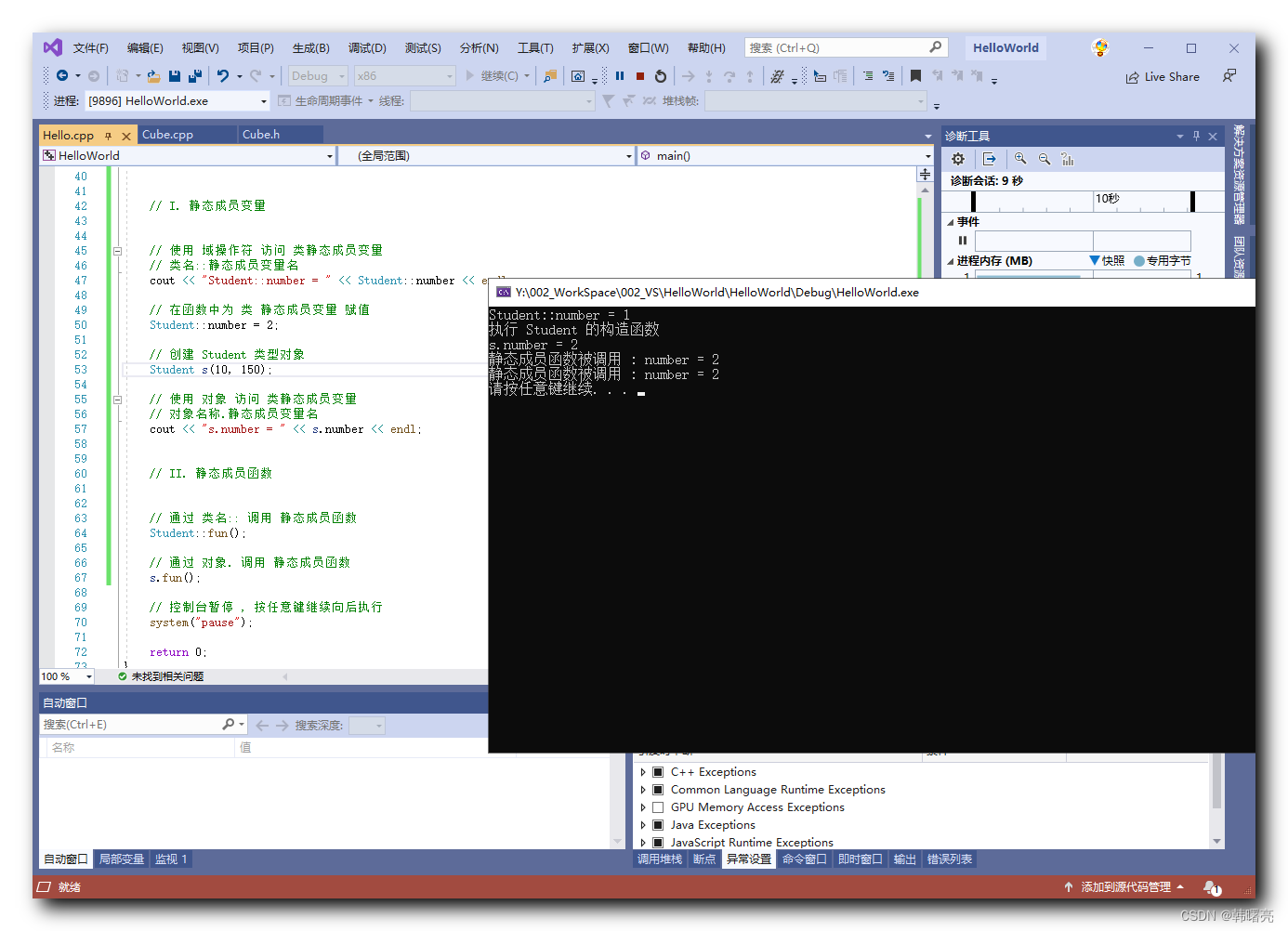
【C++】静态成员函数 ( 静态成员函数概念 | 静态成员函数声明 | 静态成员函数访问 | 静态成员函数只能访问静态成员 )
文章目录 一、静态成员函数简介1、静态成员函数概念2、静态成员函数声明3、静态成员函数访问4、静态成员函数只能访问静态成员 二、代码示例 - 静态成员函数 一、静态成员函数简介 1、静态成员函数概念 静态成员函数归属 : 在 C 类中 , 静态成员函数 是一种 特殊的函数 , 该函数…...
)
基于若依ruoyi-nbcio增加flowable流程待办消息的提醒,并提供右上角的红字数字提醒(三)
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 1、上一节说到RedisReceiver ,这里有调用了NbcioRedisListener自定义业务监听,如下…...

用友第五届开发者大赛初赛晋级公示,复赛火热进行中!
用友第五届开发者大赛初赛晋级公示,复赛火热进行中! 自7月13日鸣锣揭幕,9月6日各赛道作品初评工作完成,历时近两月,用友第五届企业云服务开发者大赛初赛阶段顺利落下帷幕。作为备受各界开发者关注的赛事,本…...

SSL证书如何做到保障网站安全?
当网站显示不安全时,用户会在头脑中产生该网站是否合法的疑问,如果是购物网站或者购物商城,那意味着可能会损失大部分的用户。而SSL证书能有效保障网站的安全性,轻松解决网站不被用户信任的问题。那么,SSL证书究竟是如…...
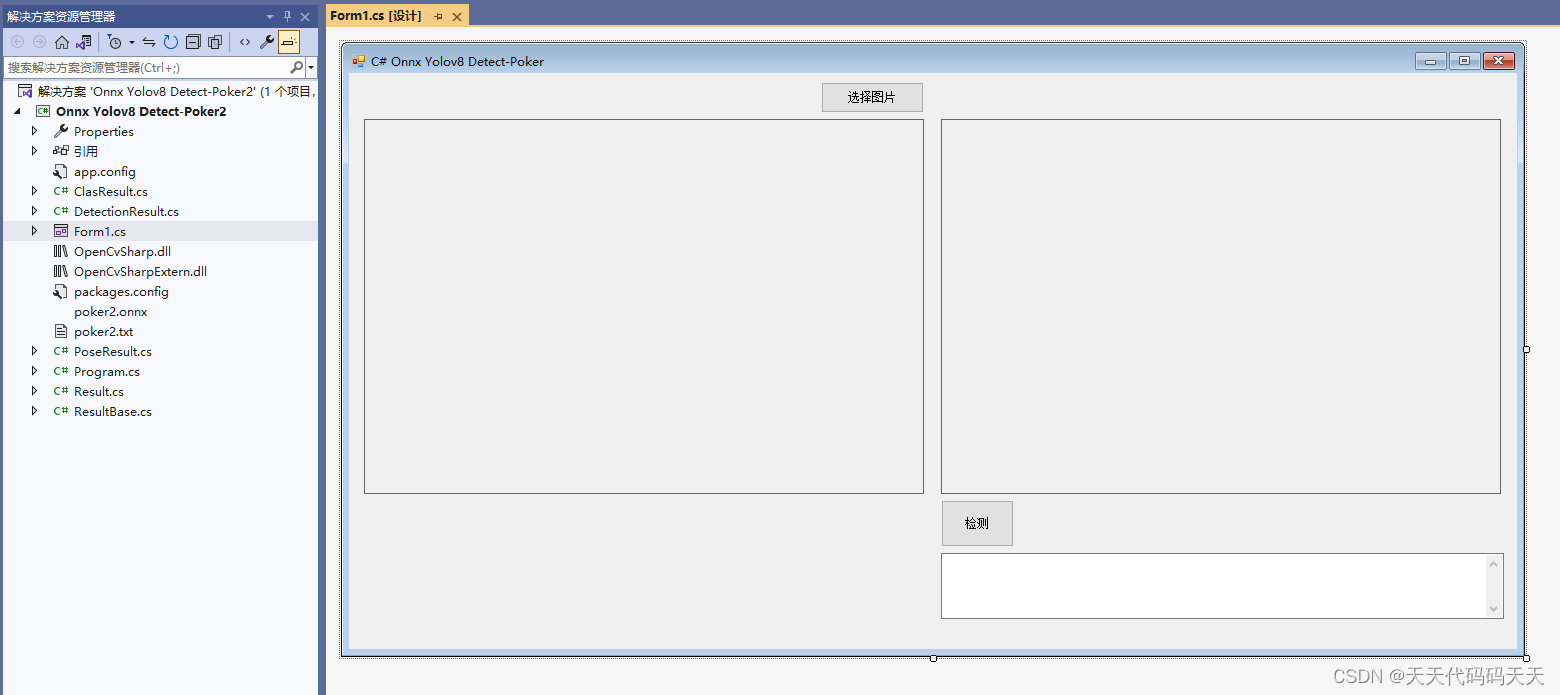
C# Onnx Yolov8 Detect Poker 扑克牌识别
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System…...

想要精通算法和SQL的成长之路 - 最长等差数列
想要精通算法和SQL的成长之路 - 最长等差数列 前言一. 最长等差数列 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 最长等差数列 原题链接 思路: 我们假设dp[i][j] 为:以num[i]为结尾,以j为公差的最长等差子序列的长度。由此可知&a…...

【简单的自动曝光】python实现-附ChatGPT解析
1.题目 一个图像有 n 个像素点,存储在一个长度为 n 的数组 img 里, 每个像素点的取值范围[0,255] 的正整数。 请你给图像每个像素点值,加上一个整数 k (可以是负数),得到新图 newImg , 使得新图newImg 的所有像素平均值最接近中位值 128。 请输出这个整数 k。 输入描述 n …...

网工内推 | 运维工程师,CCNP认证优先,周末双休,多次调薪机会
01 驻场运维 职责描述: 1、驻场某大型汽车整车厂,配合客户完成网络相关(路由交换)的项目。 2、按照客户要求,与项目组配合共同完成项目前期调研,设计,规划,项目中期调试测试&#…...

LeetCode 1337. The K Weakest Rows in a Matrix【数组,二分,堆,快速选择,排序】1224
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

如何使用Spring提供的Retry
0、本例中使用的是 springboot-2.0.4.RELEASE,jdk1.8 1、导包。需要注意版本。2.0.0需要spring6和jdk17 <dependency><groupId>org.springframework.retry</groupId><artifactId>spring-retry</artifactId><version>1.3.4<…...
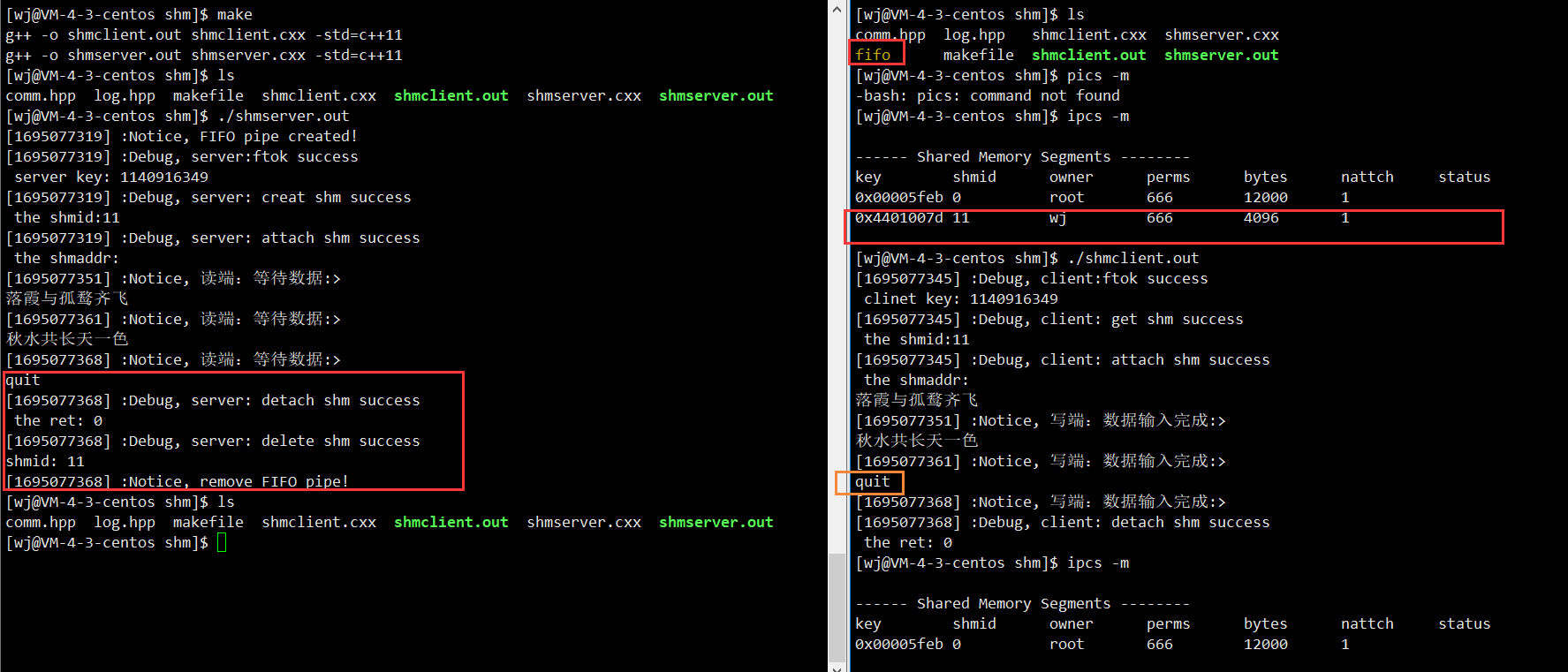
【ONE·Linux || 进程间通信】
总言 进程间通信:简述进程间通信,介绍一些通信方式,管道通信(匿名、名命)、共享内存等。 文章目录 总言1、进程间通信简述2、管道2.1、简介2.2、匿名管道2.2.1、匿名管道的原理2.2.2、编码理解:用fork来共…...
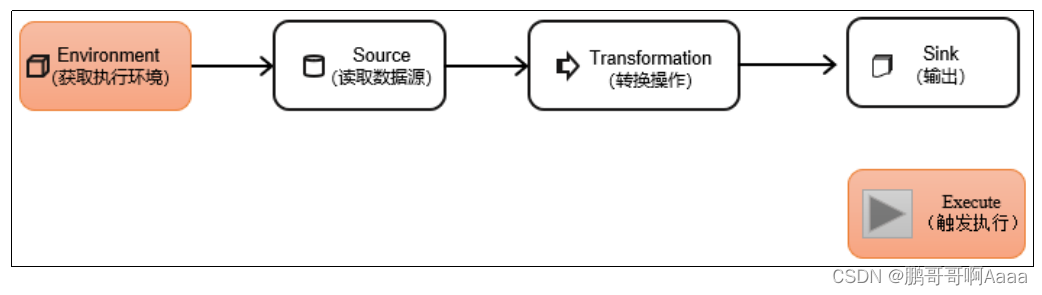
207.Flink(二):架构及核心概念,flink从各种数据源读取数据,各种算子转化数据,将数据推送到各数据源
一、Flink架构及核心概念 1.系统架构 JobMaster是JobManager中最核心的组件,负责处理单独的作业(Job)。一个job对应一个jobManager 2.并行度 (1)并行度(Parallelism)概念 一个特定算子的子任务(subtask)的个数被称之为其并行度(parallelism)。这样,包含并行子任…...
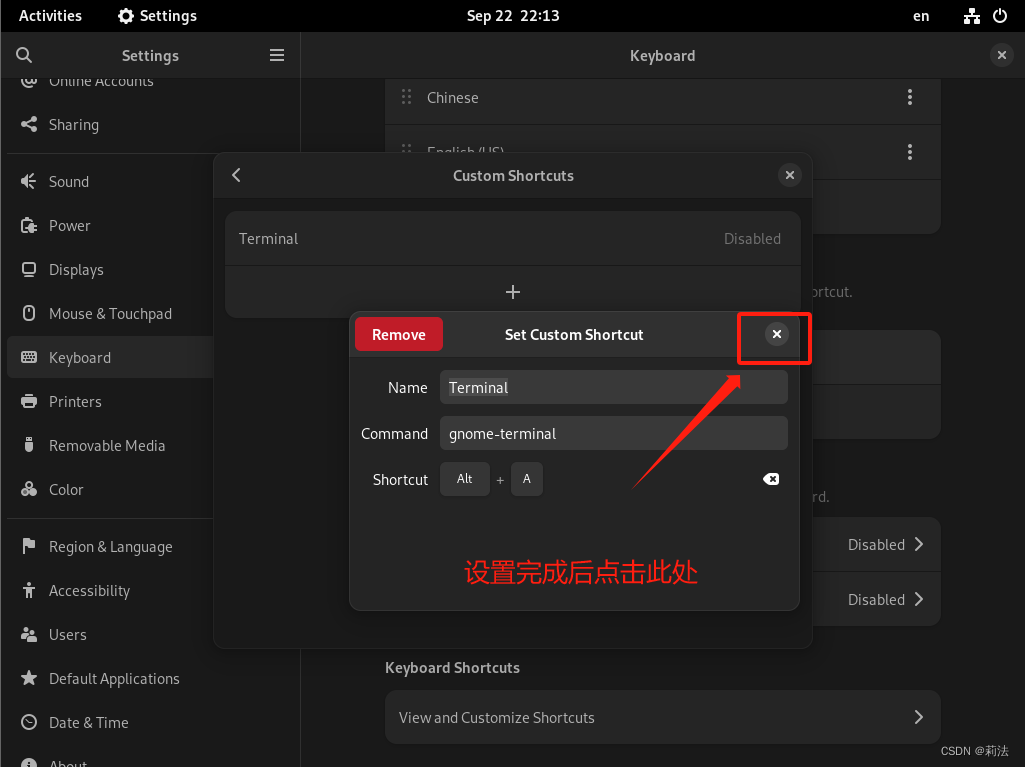
debian终端快捷键设置
为了方便使用图形化debian,快捷调出shell终端是提升工作学习效率的最重要的一步。 1.首先点击右上角,选择设置 2.点击键盘,选择快捷键,并创建自定义快捷键 3.点击添加快捷键 4.根据图中提示创建快捷键 Name: Terminal Command…...

原生ajax
什么是Ajax Asynchronous JavaScript and xml 异步的 js 和 xml(数据承载方式) ,本质:使用js提供的异步对象XMLHttpRequest 异步的向服务器提交请求,并且接受服务器响应回来的数据。 使用ajax 1.创建异步对象 var xhrnew XMLHttp…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
