【动态规划刷题 17】回文子串 最长回文子串
647. 回文子串
链接: 647. 回文子串
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = “abc”
输出:3
解释:三个回文子串: “a”, “b”, “c”
示例 2:
输入:s = “aaa”
输出:6
解释:6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”
解法(动态规划):
算法思路:
我们可以先「预处理」⼀下,将所有⼦串「是否回⽂」的信息统计在 dp 表⾥⾯,然后直接在表⾥⾯统计 true 的个数即可。
1.状态表示*
为了能表⽰出来所有的⼦串,我们可以创建⼀个 n * n 的⼆维 dp 表,只⽤到「上三⻆部分」
即可。
其中, dp[i][j] 表⽰: s 字符串 [i, j] 的⼦串,是否是回⽂串。
2.状态转移方程
对于回⽂串,我们⼀般分析⼀个「区间两头」的元素:
- 当 s[i] != s[j] 的时候:不可能是回⽂串, dp[i][j] = 0 ;
- 当 s[i] == s[j] 的时候:根据⻓度分三种情况讨论:
• ⻓度为 1 ,也就是 i == j :此时⼀定是回⽂串,dp[i][j] = true ;
• ⻓度为 2 ,也就是 i + 1 == j :此时也⼀定是回⽂串, dp[i][j] =true ;
• ⻓度⼤于 2 ,此时要去看看 [i + 1, j - 1] 区间的⼦串是否回⽂: dp[i][j]= dp[i + 1][j - 1] 。
综上,状态转移⽅程分情况谈论即可。
3. 初始化
因为我们的状态转移⽅程分析的很细致,因此⽆需初始化。
4. 填表顺序
根据「状态转移⽅程」,我们需要「从下往上」填写每⼀⾏,每⼀⾏的顺序⽆所谓
5. 返回值
根据「状态表⽰和题⽬要求」,我们需要返回 dp 表中 true 的个数
代码:
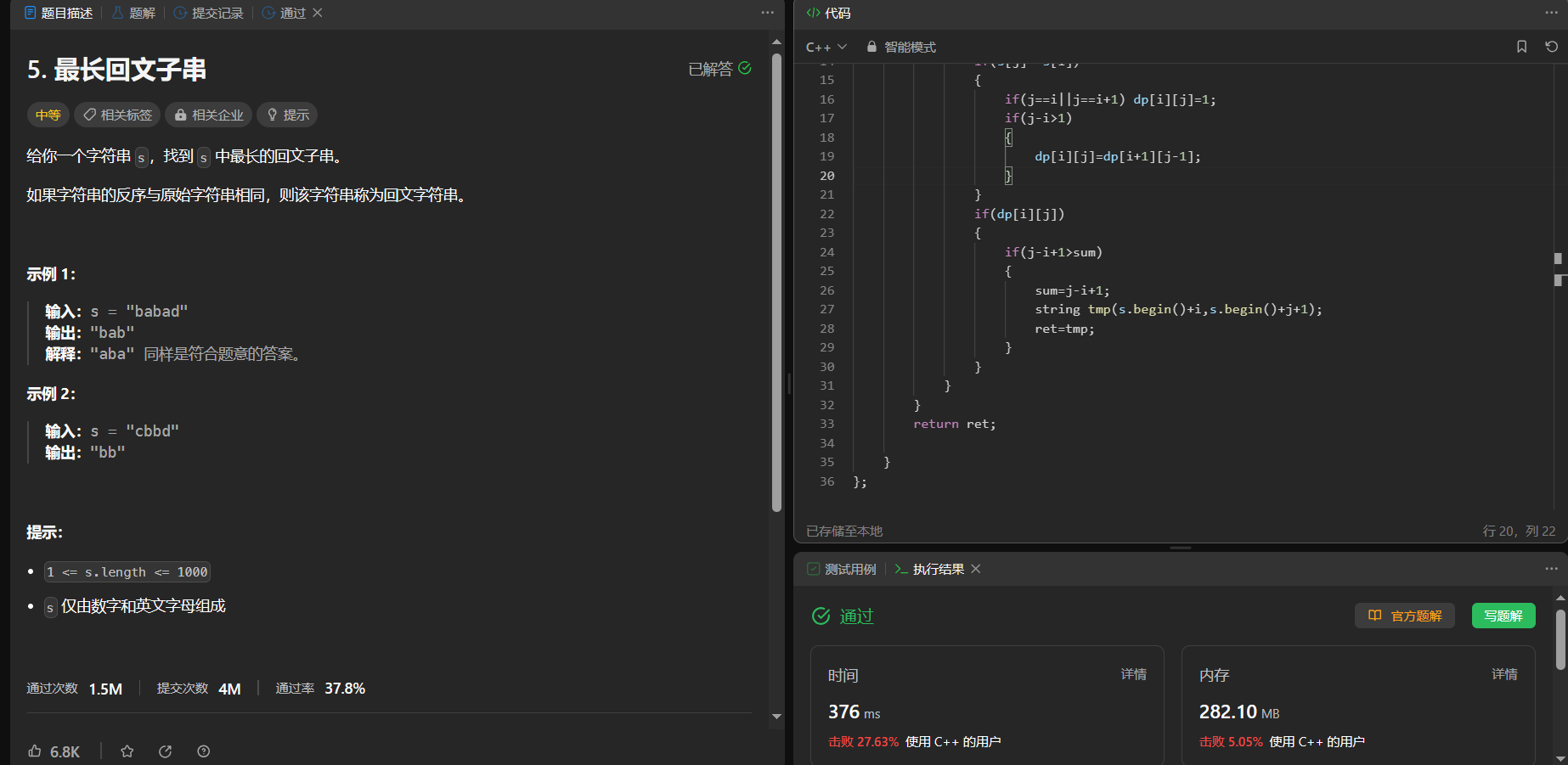
int countSubstrings(string s) {int n=s.size();vector<vector<int>> dp(n,vector<int>(n));dp[0][0]=1;int sum=1;for(int j=1;j<n;j++){for(int i=0;i<=j;i++){if(s[j]==s[i]){if(j==i||j==i+1) dp[i][j]=1;if(j-i>1){dp[i][j]=dp[i+1][j-1];}}if(dp[i][j]) sum++;}}return sum;}
5. 最长回文子串
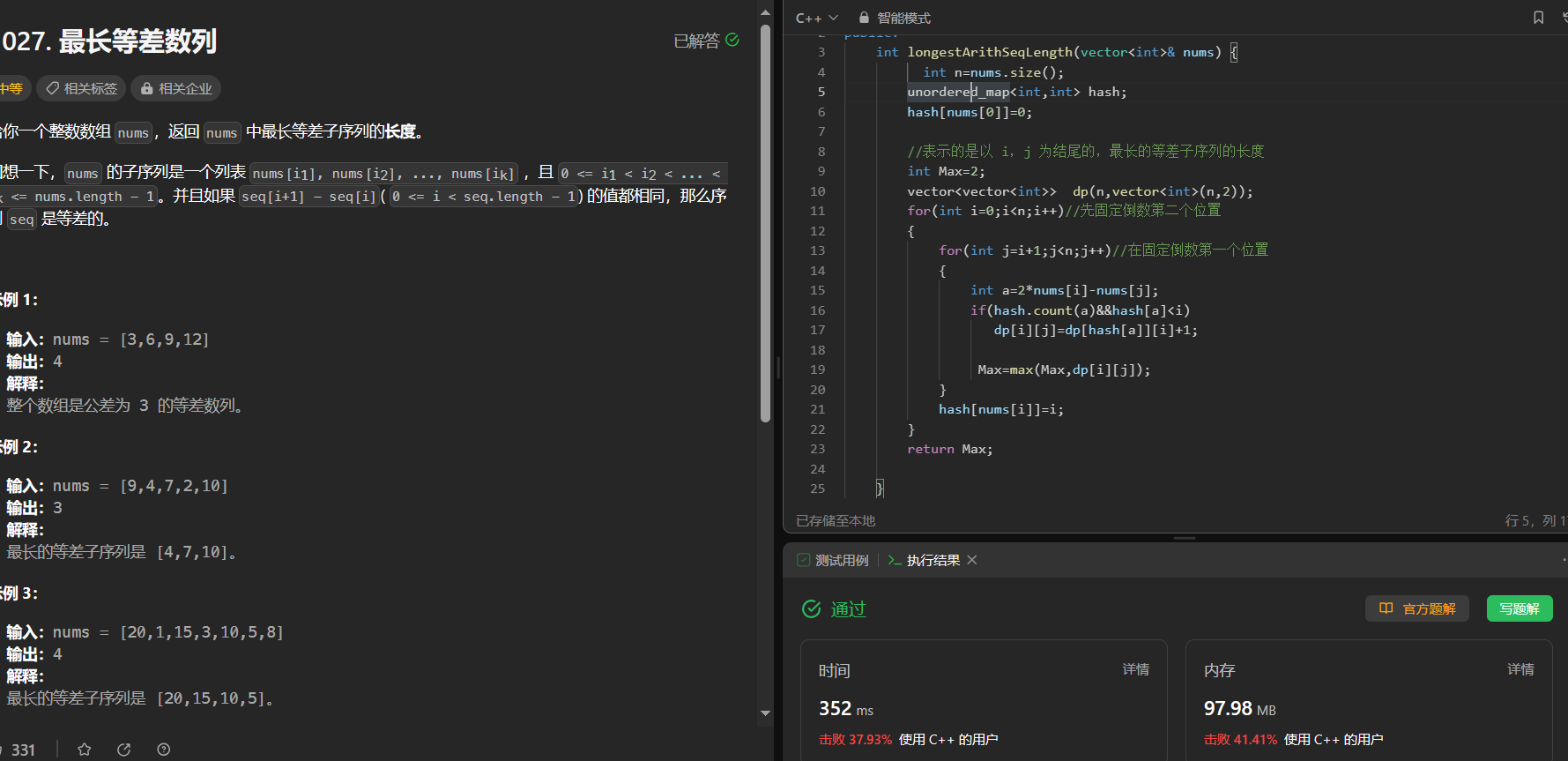
链接: 5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = “babad”
输出:“bab”
解释:“aba” 同样是符合题意的答案。
示例 2:
输入:s = “cbbd”
输出:“bb”
解法思路:
- a. 我们可以先⽤ dp 表统计出「所有⼦串是否回⽂」的信息
- b. 然后根据 dp 表⽰ true 的位置,得到回⽂串的「起始位置」和「⻓度」。 那么我们就可以在表中找出最⻓回⽂串。
关于「预处理所有⼦串是否回⽂」,已经在上⼀道题⽬⾥已经讲解过了。
代码:
string longestPalindrome(string s) {int n=s.size();vector<vector<int>> dp(n,vector<int>(n));dp[0][0]=1;int sum=1;string ret(1,s[0]);for(int j=1;j<n;j++){for(int i=0;i<=j;i++){if(s[j]==s[i]){if(j==i||j==i+1) dp[i][j]=1;if(j-i>1){dp[i][j]=dp[i+1][j-1];}}if(dp[i][j]){if(j-i+1>sum){sum=j-i+1;string tmp(s.begin()+i,s.begin()+j+1);ret=tmp;}}}}return ret;}
相关文章:

【动态规划刷题 17】回文子串 最长回文子串
647. 回文子串 链接: 647. 回文子串 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串,即使是由…...

mysql 每日自动备份数据库
在 MySQL 中,你可以使用定时任务来每日自动备份数据库。通常,最常用的方法是使用操作系统的定时任务工具(如cron)来调度备份操作。以下是一些步骤来设置每日定时备份MySQL数据库: 创建备份脚本:首先&#x…...

【计算机网络】图解路由器(二)
本系列包含: 图解路由器(一)图解路由器(二) 图解路由器(二) 21、什么是静态路由?22、什么是动态路由?23、动态路由有哪些类型?24、什么是 RIP ?2…...
流媒体及直播相关知识
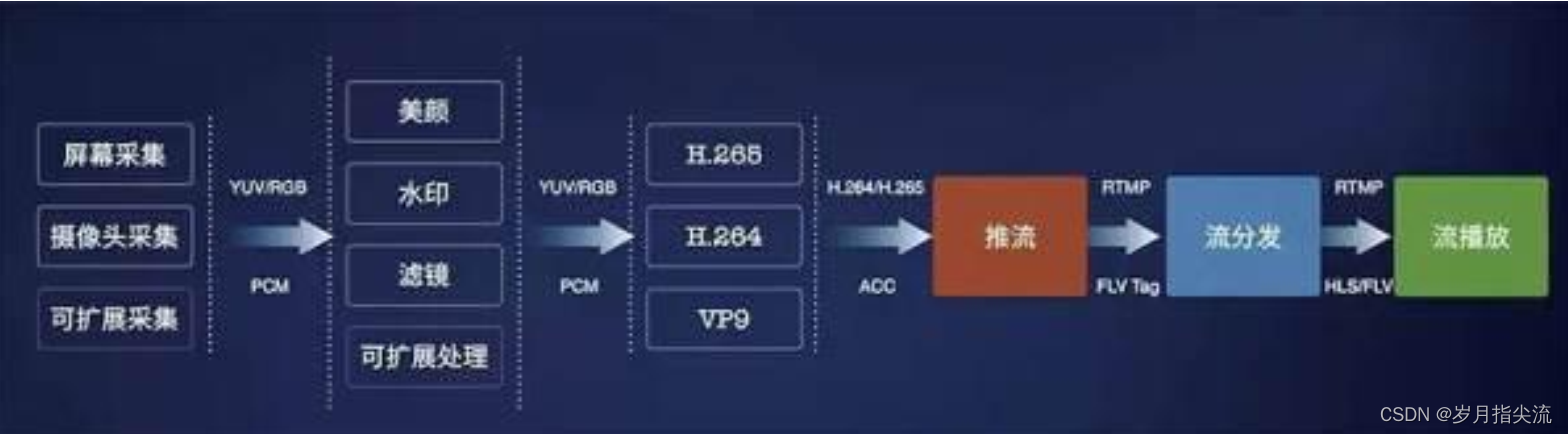
文章目录 前言一、流媒体1、基本概念2、流式传输3、流媒体技术原理4、流媒体传输模式5、H.264 流媒体传输系统框架 二、直播1、直播中使用的流媒体协议2、直播的模块划分3、视频直播流程①、推流到服务器②、服务器流分发 前言 本文主要讲解流媒体及其直播相关知识,…...
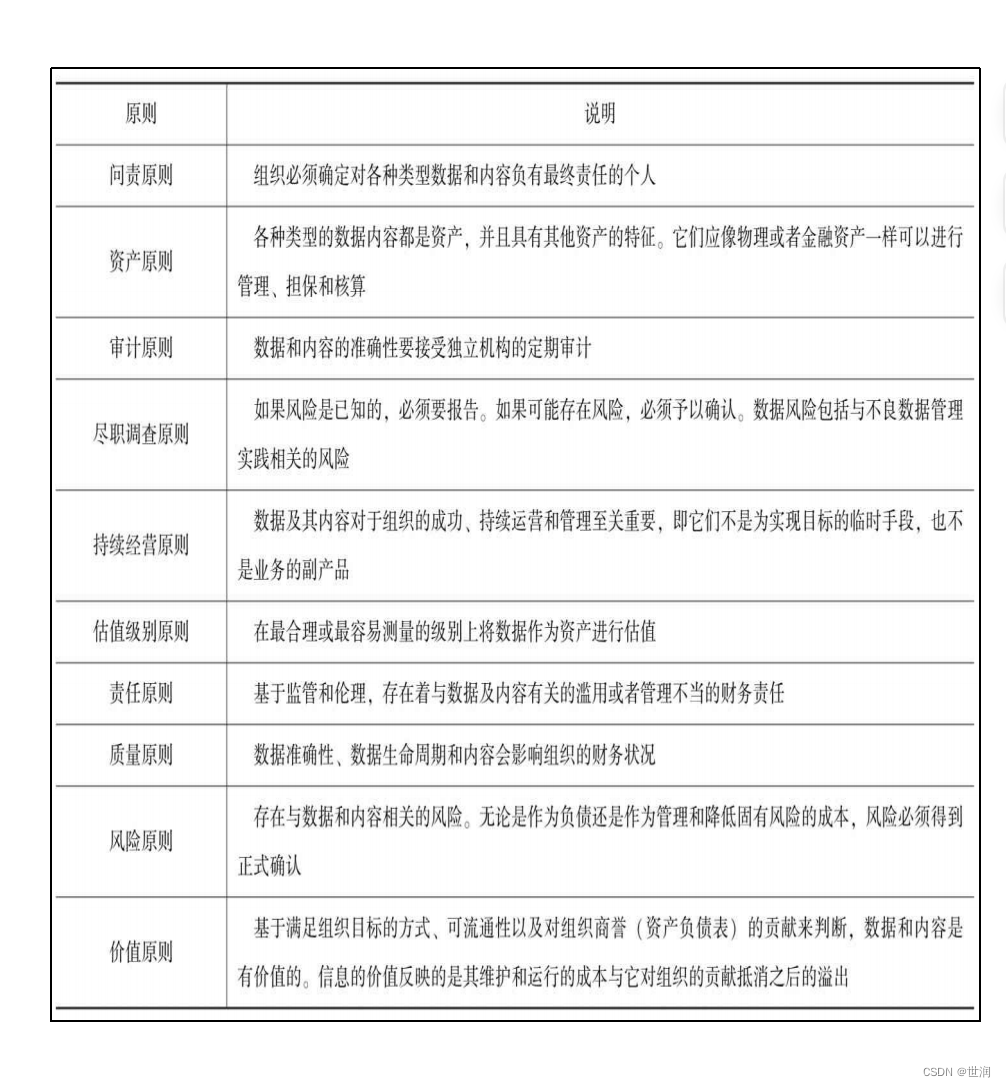
数据治理-数据资产估值
数据生命周期大多数阶段涉及成本。数据只有使用时才有价值,使用时数据还产生与风险相关的成本。因此,当使用数据的经济效益超过了上述成本时,就会显现其价值。 其他的度量价值的方式包括: 替换成本。数据替换或恢复的成本。包括组…...

点云从入门到精通技术详解100篇-机载 LiDAR 点云滤波及分类
目录 前言 国内外研究现状 点云滤波研究现状 点云分类研究现状...

【SLAM】 前端-视觉里程计之相对位姿估计
【SLAM】 前端-视觉里程计之相对位姿估计 1.相对位姿估计 在前端视觉里程计中,相对位姿估计是指通过视觉传感器(例如相机)捕捉的图像信息,来估计相机相对于先前位置的位姿(位置和姿态)变化。这种估计通常…...

git format-patch打补丁
git format-patch HEAD^ 这个命令会产生从倒数第二个提交 HEAD^ 到最后提交 HEAD 之间所有提交的差异,并生成一个包含这些差异的补丁文件。这是一个包含详细步骤的例子: 第一步,创建一个新的 git 仓库并进行一些提交。这些提交是我们稍后会生…...

大数据Flink(八十三):SQL语法的DML:With、SELECT WHERE、SELECT DISTINCT 子句
文章目录 SQL语法的DML:With、SELECT & WHERE、SELECT DISTINCT 子句 一、DML:With 子句...
C++:list
目录 List的模拟实现 List节点类 List链表结构 List迭代器类 结构 T& operator*(); T& operator->(); Self& operator(); Self operator(int); Self& operator--(); Self& operator--(int); bool operator!(const Self& l); bool oper…...
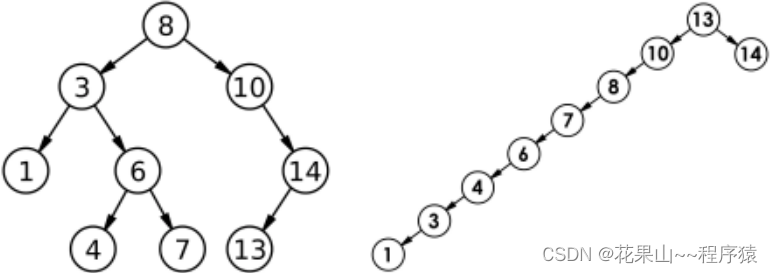
【C++】搜索二叉树底层实现
目录 一,概念 二,实现分析 1. 插入 (1.)非递归版本 (2.)递归版本 2. 打印搜索二叉树 3.查找函数 (1.)非递归版本 (2.)递归版本 4. 删除函数&#x…...

C8051F020 SMBus一直处于busy状态解决办法
当SMBus总线处于busy状态切且无法自动释放时,SMB0CN寄存器的第7位一直为 1,总线没有释放。 SMBus总线释放超时的一个纠错机制,它允许SMBus状态机在 SDA 和 SCL 信号线同为高电平超过 10个SMBus时钟源周期后判断总线为释放状态。 如果总线释放…...

Activiz 9.2 for Linux Crack
Activiz 9.2 在 C#、.Net 和 Unity 软件中为您的 3D 内容释放可视化工具包的强大功能。 ActiViz 允许您轻松地将 3D 可视化集成到您的应用程序中。 ActiViz 功能 用 C# 封装的 3D 可视化软件系统 允许在 .NET 环境中快速开发可投入生产的交互式3D 应用程序 支持窗口演示基础 (…...

数据结构 - 链表
线性表的链式存储结构 概念 将线性表 L (a0, a1, … , an-1)中各元素分布在存储器的不同存储块,成为结点,通过地址或指针建立元素之间的联系。 结点的 data 域存放数据元素 ai ,而 next 域是一个指针,指向 ai 的直接后继 ai1 …...

Android 12 Bluetooth源码分析蓝牙配对
本文主要是列出一些蓝牙配对重要的类和方法/函数,遇到相关问题时方便查找添加log排查。 蓝牙扫描列表页面:packages/apps/Settings/src/com/android/settings/bluetooth/DeviceListPreferenceFragment.java点击其中一个设备会调用:onPrefere…...
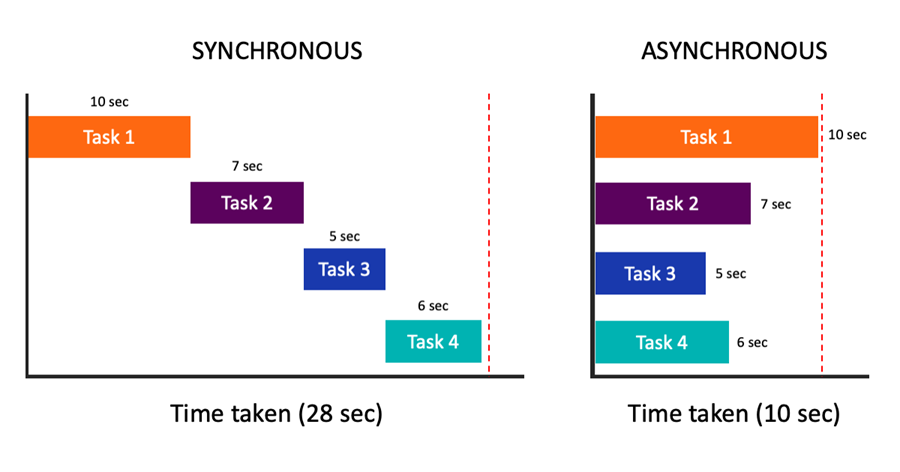
Python异步编程并发执行爬虫任务,用回调函数解析响应
一、问题:当发送API请求,读写数据库任务较重时,程序运行效率急剧下降。 异步技术是Python编程中对提升性能非常重要的一项技术。在实际应用,经常面临对外发送网络请求,调用外部接口,或者不断更新数据库或文…...

React组件化开发
1.组件的定义方式 函数组件Functional Component类组件Class Component 2.类组件 export class Profile extends Component {render() {console.log(this.context);return (<div>Profile</div>)} } 组件的名称是大写字符开头(无论类组件还是函数组件…...
--crypto - 加解密和hash函数)
LuatOS-SOC接口文档(air780E)--crypto - 加解密和hash函数
crypto.md5(str) 计算md5值 参数 传入值类型 解释 string 需要计算的字符串 返回值 返回值类型 解释 string 计算得出的md5值的hex字符串 例子 -- 计算字符串"abc"的md5 log.info("md5", crypto.md5("abc"))crypto.hmac_md5(str, k…...

自动化测试的定位及一些思考
大家对自动化的理解,首先是想到Web UI自动化,这就为什么我一说自动化,公司一般就会有很多人反对,因为自动化的成本实在太高了,其实自动化是分为三个层面的(UI层自动化、接口自动化、单元测试)&a…...
展会动态 | 迪捷软件邀您参加2023世界智能网联汽车大会
*9月18日之前注册的观众免收门票费* 由北京市人民政府、工业和信息化部、公安部、交通运输部和中国科学技术协会联合主办的2023世界智能网联汽车大会将于9月21日-24日在北京中国国际展览中心(顺义馆)举行。 论坛背景 本届展会以“聚智成势 协同向新——…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
