怎么找回电脑删除的图片
怎么找回电脑删除的图片?图片作为一种非常简单方便的文件,经常被用来辅助我们的日常工作和学习。但在我们整理电脑时,如果我们不小心手一抖就删除了一些重要的图片,遇到这种事我们要如何才能恢复呢?
众所周知,简单的删除并不会完全抹掉照片,会暂存在回收站里,就是为了防止这种误操作造成文件丢失。
这时候我们只需要打开回收站;
找到要删除的图片并选中;
右键菜单中选择还原。然后,它们将恢复到原始位置。
如果没有找到,我们可以在电脑中的:备份和恢复,您也可以在没有软件的情况下帮助恢复电脑中已删除的照片,但前提是您之前已经启用了该功能。
打开我们的控制面板,选择系统和安全,点击备份和还原。
选择“从备份还原文件”,然后按照说明进行操作。
浏览或搜索备份图片,然后选择一个位置来恢复它们。
如果我们已经清空了回收站,未进行备份,无法通过电脑系统恢复,必须求助专业的数据恢复软件。下面小编就以这款软件为例,给大家演示一下具体的操作方式:
第一步:运行失易得数据恢复软件,选择“误删除文件”或者“深度恢复”功能进入。
第二步:根据您删除图片之前保存文件的位置进行选择,也就是文件所在的磁盘,点击下一步。
第三步:选择我们要恢复的文件类型,这里我们可以选择图片。然后点击进行扫描。
第四步:等待扫描完毕,找到我们要恢复的文件进行预览,确认是我们要恢复的文件后,勾选要恢复的文件,点击恢复按钮,选择文件要保存的路径,即可恢复成功。
以上就是关于怎么找回电脑删除的图片的方法,希望能帮助你解决目前遇到的问题。
相关文章:

怎么找回电脑删除的图片
怎么找回电脑删除的图片?图片作为一种非常简单方便的文件,经常被用来辅助我们的日常工作和学习。但在我们整理电脑时,如果我们不小心手一抖就删除了一些重要的图片,遇到这种事我们要如何才能恢复呢? 众所周知,简单的删除并不会完…...

【Linux】进程状态与进程优先级
目录一.进程状态1.阻塞:2.挂起:具体情况3.具体操作系统状态变化R:运行状态(running)S:休眠状态(sleeping)D:磁盘休眠状态(Disk sleep)T:暂停状态(stopped)暂停进程继续进程t:追踪暂停状态(traci…...

Python+Qt生日提醒
PythonQt生日提醒如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助!前言这篇博客针对<<PythonQt生日提醒>>编写代码,代码整洁,规则,易读。 学习与应用推荐首选。文章目…...
第二章 编写MBR主引导记录
主引导记录(MBR,Master Boot Record)是采用MBR分区表的硬盘的第一个扇区,即C/H/S地址的0柱面0磁头1扇区,也叫做MBR扇区 计算机的启动过程 为什么程序要载入内存 CPU的硬件电路被设计成只能运行处于内存中的程序&…...
Android 9.0 仿ios的hotseat效果修改hotseat样式
1.概述 在9.0的系统rom定制化的产品中,在launcher3的定制化需求中,有很多功能需求点需要开发,在对一下ui的定制化的过程中,会参考ios的样式进行定制化,所以最近项目需求 要求仿ios的hotseat的样式来进行产品的定制,开发一款仿ios的hotseat,所以需要对hotseat进行分析,然…...

量化私募投资百亿头部量化私募企业在招岗位:AI算法工程师21/22/23届,校招/秋招/社招都看年base60-200万
量化私募投资百亿头部量化私募企业在招岗位:AI算法工程师21/22/23届,校招/秋招/社招都看年base60-200万bonuscut965制度应届需要985本硕博有3年以上相关ai算法经验可放宽学历"岗位职责:base 北京 上海 杭州 深圳1. 利用机器学习、深度学习和人工智能…...

百度西交大大数据菁英班目标检测竞赛
来源:投稿 作者:LSC 编辑:学姐 数据介绍 数据集共包括40000张训练图像和1000张测试图像,每张训练图像对应xml标注文件: 共包含3类:0:head, 1:helmet, 2:person。 提交格式要求,提交名为pred_r…...
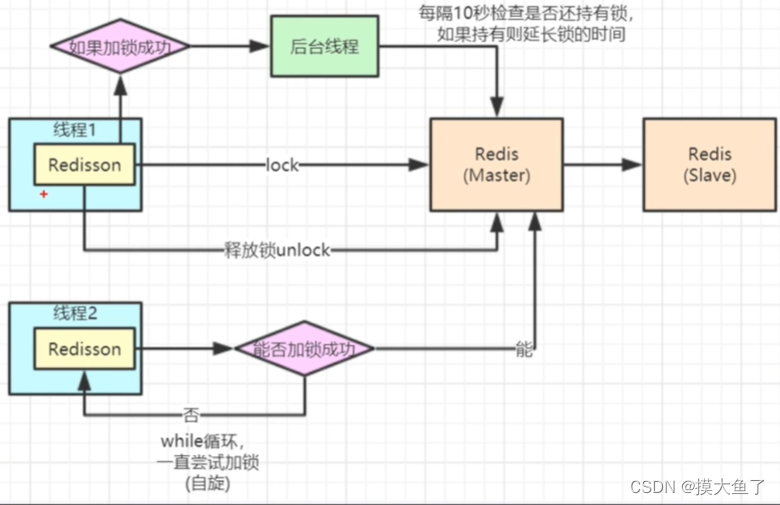
Redisson实现分布式锁
目录Redisson简介Redisson实现分布式锁步骤引入依赖application.ymlRedisson 配置类Redisson分布式锁实现Redisson简介 Redis 是最流行的 NoSQL 数据库解决方案之一,而 Java 是世界上最流行(注意,没有说“最好”)的编程语言之一。…...

【HID基础知识】
蓝牙HID基础知识 一:定义 HID是Human Interface Device的缩写,由其名称可以了解HID设备是直接与人交互的设备,例如键盘、鼠标与游戏手柄等。 蓝牙HID 是属于蓝牙协议里面的一个profile, 不管在蓝牙2.0 2.1 3.0还是4.0,5.0的蓝牙中…...

工赋开发者社区 | 工业数字孪生:西门子工业网络与设备虚拟调试案例(TIA+MCD+SINETPLAN)
PART1案例背景及基本情况新生产系统的设计和实施通常是耗时且高成本的过程,完成设计、采购、安装后,在移交生产运行之前还需要一个阶段,即调试阶段。如果在开发过程中的任何地方出现了错误而没有被发现,那么每个开发阶段的错误成本…...
将闲置的Ipad作为Windows的副屏(Twomon SE)
目录一、前言二、方法第一步 安装软件第二步 使用步骤三、注意一、前言 在看网课的时候,总有种不得劲的感觉,来来回回的切换就很糟心~~无意间看见闲置的板砖(Ipad),计上心来-- _ – 期间也尝试过免费的软件ÿ…...

浮点数在内存中的存储——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容是浮点数在内存中的存储,昨天我们已经写过了整型在内存中的存储,那么,浮点数在内存中是怎样存储的呢?现在,就让我们进入浮点数在内存中的存储的世界吧…...

华为OD机试 C++ 实现 - 租车骑绿岛
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...
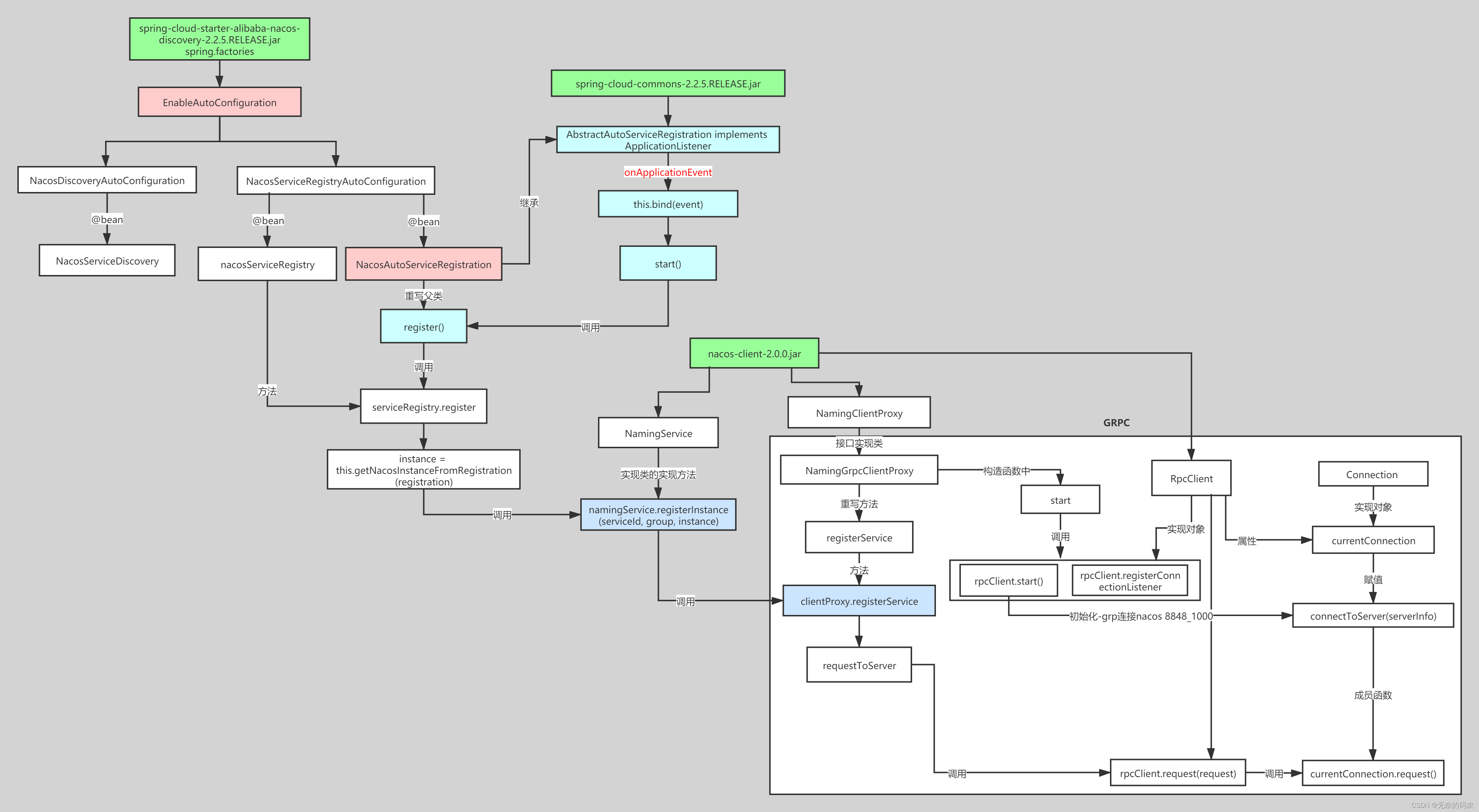
Spring Cloud Nacos源码讲解(三)- Nacos客户端实例注册源码分析
Nacos客户端实例注册源码分析 实例客户端注册入口 流程图: 实际上我们在真实的生产环境中,我们要让某一个服务注册到Nacos中,我们首先要引入一个依赖: <dependency><groupId>com.alibaba.cloud</groupId><…...

位运算(C/C++)
1. 基础知识 程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。比如,and运算本来是一个逻辑运算符,但整数与整数之间也可以进行and运算。举个例子,6的二进制是110,11的二…...

哈希表题目:设计哈希映射
文章目录题目标题和出处难度题目描述要求示例数据范围前言解法一思路和算法代码复杂度分析解法二思路和算法代码复杂度分析题目 标题和出处 标题:设计哈希映射 出处:706. 设计哈希映射 难度 3 级 题目描述 要求 不使用任何内建的哈希表库设计一个…...

力扣解法汇总1238. 循环码排列
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接: 力扣 描述: 给你两个整数 n 和 start。你的任务是返回任意 (0,1,2,,...,2^n-1) 的排列 p&…...
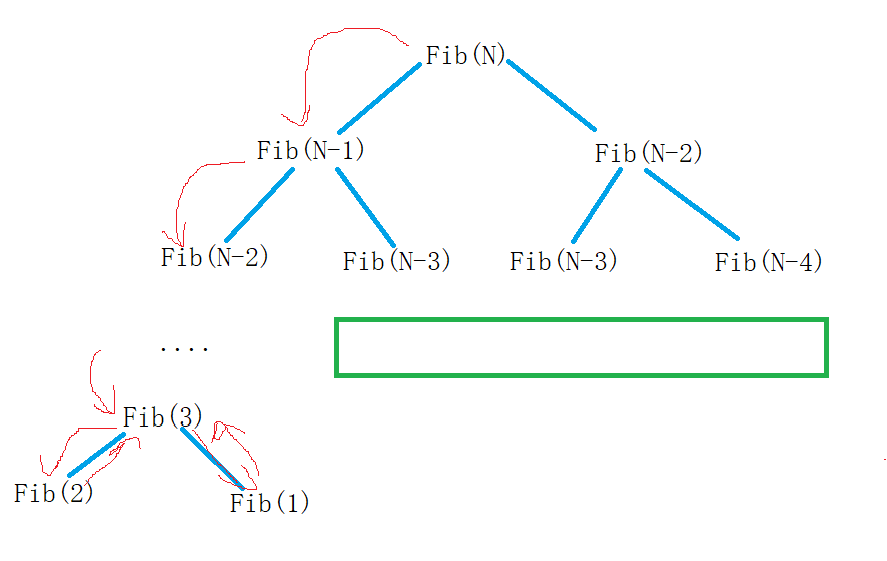
[数据结构]时间复杂度与空间复杂度
[数据结构]时间复杂度与空间复杂度 如何衡量一个算法的好坏 long long Fib(int N) {if(N < 3)return 1;return Fib(N-1) Fib(N-2); } 这是一个求斐波那契数列的函数,使用递归的方法求得,虽然代码看起来很简洁,但是简洁真的就好吗&#…...

Codeforces Round #848 (Div. 2)(A~D)
A. Flip Flop Sum给出一个只有1和-1的数组,修改一对相邻的数,将它们变为对应的相反数,修改完后数组的和最大是多少。思路:最优的情况是修改一对-1,其次是一个1一个-1,否则修改两个1。AC Code:#i…...
)
第十三届蓝桥杯Java B 组国赛 C 题——左移右移(AC)
目录1.左移右移1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围6.原题链接2.解题思路3.Ac_code1.左移右移 1.题目描述 小蓝有一个长度为 NNN 的数组, 初始时从左到右依次是 1,2,3,…N1,2,3, \ldots N1,2,3,…N 。 之后小蓝对这个数组进行了 MMM 次操作, 每次…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
