位运算(C/C++)
1. 基础知识
程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。比如,and运算本来是一个逻辑运算符,但整数与整数之间也可以进行and运算。举个例子,6的二进制是110,11的二进制是1011,那么6 and 11的结果就是2,它是二进制对应位进行逻辑运算的结果(0表示False,1表示True)。
在一个二进制数中,最右边的位称为第 0 位,从右往左一次递增。

2. 位运算的常见运用
2.1 求一个数N的二进制表示中第k位是几?
解题步骤:1:把二进制数的第 k 位移动到第 0 位,即:N >> k。
2:将移动后的结果 & 1,得到的数即是最的结果。
例如:一个整数10,求它的二进制表示中第三位是几?10 的二进制表示为:1010,向右移动 3 位:0001。0001 & 1 = 1,故 10 的第三位是 1。
2.2 一个数N的二进制中最右侧的1
例如:一个数的二进制表示为:10101000,则将最右侧的 1 连同后面的 0 一起,输出该二进制串表示的数字,即:1000 表示的数字 8。
解题方法:将该数去进行一个 lowbit 操作就行。lowbit(x) : x & (-x)。
下面以整数 int N = 40 来举例分析。我们可以先求出结果:40 的二进制表示为:101000,最终结果就是1000 表示的数字 8 。

剑指 Offer 15. 二进制中1的个数 - 力扣(LeetCode)
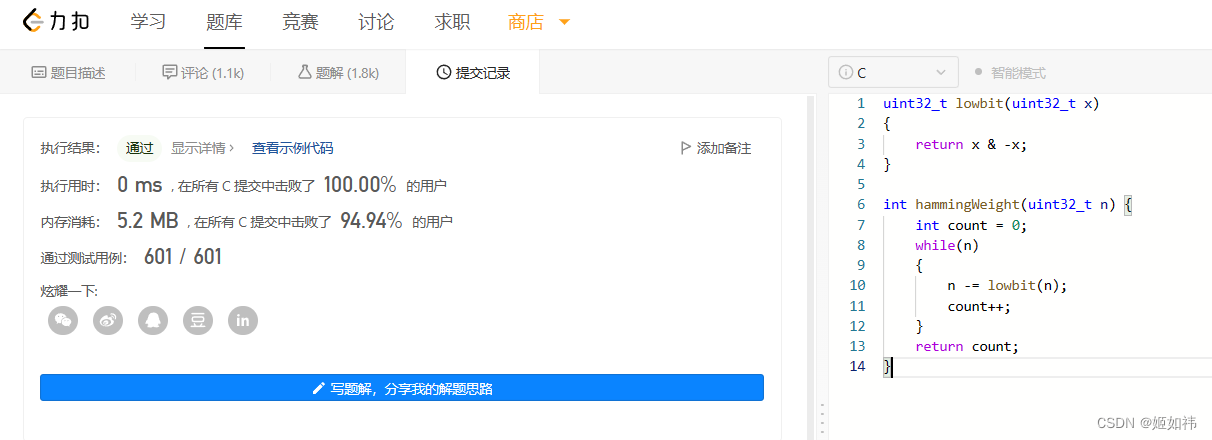
题目描述:编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为 汉明重量).)。
有了上面 lowbit(N) 的思路,相比之前的讲解又可以得到一种新的解法了。
http://t.csdn.cn/oIMpd![]() http://t.csdn.cn/oIMpd解题思路:我们将 n 进行 lowbit 操作,然后让 n 减去 lowbit 的结果,直到 n 为0,统计减去的次数即为结果。
http://t.csdn.cn/oIMpd解题思路:我们将 n 进行 lowbit 操作,然后让 n 减去 lowbit 的结果,直到 n 为0,统计减去的次数即为结果。
uint32_t lowbit(uint32_t x)
{return x & -x;
}int hammingWeight(uint32_t n) {int count = 0;while(n){n -= lowbit(n);count++;}return count;
}
2.3 交换两个数
有道笔试题是这样的:给你两个数 A,B,在不使用第三个变量的前提下交换 A,B。
这道题可以用 加法的方式求解。我们这里讲解位运算的方式哈。代码如下:
int main()
{int A = 1, B = 0;A = A ^ B;B = A ^ B;A = A ^ B;printf("A: %d B: %d", A, B);return 0;
}

关于这个就是:B ^ B = 0。A ^ B ^ B = A ^ 0 = A。只需要把握住这一点就行了。
原题链接:
面试题 17.04. 消失的数字 - 力扣(LeetCode)
题目描述:数组
nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗?
将缺少一个元素的数组全部异或,结果在与不缺少的数组异或,其中相等的数字会被异或掉,剩下的就是缺失的数字(两次异或中只有一个的数字)。注意:异或是支持交换律和结合律的。
例如:缺失的数组为:0 1 3,那么缺失的数字就是:0 ^ 1 ^ 3 ^ 0 ^ 1 ^ 2 ^ 3 = 2。将缺失的数组与完整的数组异或。
int missingNumber(int* nums, int numsSize){int r = 0;for(int i = 0; i< numsSize;i++){r^=nums[i];}for(int i = 0; i <= numsSize;i++){r^=i;}return r;
}
相关文章:

位运算(C/C++)
1. 基础知识 程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。比如,and运算本来是一个逻辑运算符,但整数与整数之间也可以进行and运算。举个例子,6的二进制是110,11的二…...

哈希表题目:设计哈希映射
文章目录题目标题和出处难度题目描述要求示例数据范围前言解法一思路和算法代码复杂度分析解法二思路和算法代码复杂度分析题目 标题和出处 标题:设计哈希映射 出处:706. 设计哈希映射 难度 3 级 题目描述 要求 不使用任何内建的哈希表库设计一个…...

力扣解法汇总1238. 循环码排列
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接: 力扣 描述: 给你两个整数 n 和 start。你的任务是返回任意 (0,1,2,,...,2^n-1) 的排列 p&…...
[数据结构]时间复杂度与空间复杂度
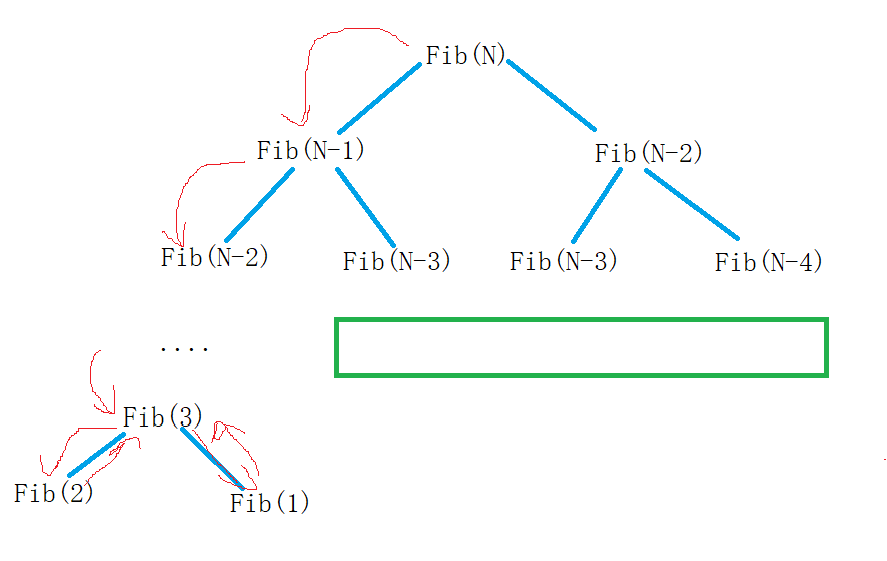
[数据结构]时间复杂度与空间复杂度 如何衡量一个算法的好坏 long long Fib(int N) {if(N < 3)return 1;return Fib(N-1) Fib(N-2); } 这是一个求斐波那契数列的函数,使用递归的方法求得,虽然代码看起来很简洁,但是简洁真的就好吗&#…...

Codeforces Round #848 (Div. 2)(A~D)
A. Flip Flop Sum给出一个只有1和-1的数组,修改一对相邻的数,将它们变为对应的相反数,修改完后数组的和最大是多少。思路:最优的情况是修改一对-1,其次是一个1一个-1,否则修改两个1。AC Code:#i…...
)
第十三届蓝桥杯Java B 组国赛 C 题——左移右移(AC)
目录1.左移右移1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围6.原题链接2.解题思路3.Ac_code1.左移右移 1.题目描述 小蓝有一个长度为 NNN 的数组, 初始时从左到右依次是 1,2,3,…N1,2,3, \ldots N1,2,3,…N 。 之后小蓝对这个数组进行了 MMM 次操作, 每次…...

第14篇:系列二—Java抽象类/接口/枚举
目录 1、继承的定义(Inheritance) 2、继承的优点 2.1 易维护性 2.2 复用性 2.3 条理性...
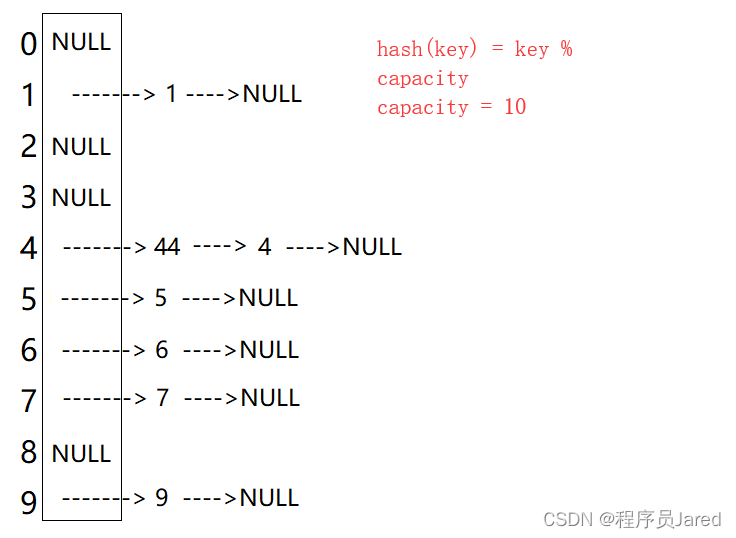
深入浅出C++ ——哈希
文章目录前言一、unordered系列关联式容器1. unordered_map2. unordered_set二、哈希1. 哈希概念2. 哈希冲突3. 哈希函数4. 哈希冲突解决方法三、模拟实现unordered系列容器1. 哈希表的改造2. 模拟实现 unordered_set3. 模拟实现 unordered_map前言 在C11中,STL又提…...

Tina_Linux_系统裁剪_开发指南
文章目录Tina_Linux_系统裁剪_开发指南1 概述2 Tina系统裁剪简介2.1 boot0裁剪2.2 uboot裁剪2.3 内核裁剪2.3.1 删除不使用的功能2.3.2 删除不使用的驱动2.3.3 修改内核源代码2.3.3.1 size工具.2.3.3.2 ksize.py脚本2.3.3.3 nm命令2.3.3.4 kernel压缩方式.2.4 文件系统裁剪.2.4…...

算法刷题打卡第99天:至少在两个数组中出现的值
至少在两个数组中出现的值 难度:简单 给你三个整数数组 nums1、nums2 和 nums3 ,请你构造并返回一个 元素各不相同的 数组,且由 至少 在 两个 数组中出现的所有值组成。数组中的元素可以按 任意 顺序排列。 示例 1: 输入&…...

线程池面试题
1. 什么是线程池?为什么要使用线程池? 线程池是一种用于管理线程的技术,它可以在应用程序中重复使用一组线程来执行多个任务。线程池的优点包括提高应用程序的性能和可伸缩性、避免线程创建和销毁的开销、避免线程过多导致系统负担过重等。线…...

【学习笔记】NOIP爆零赛5
说实话是不想补题的。因为每一道题都贼难写,题解又通篇写着显然,然后自己天天搞竞赛又把注意力搞差了,调一道题又调半天,考试的题又难的要死 不会正解 ,部分分又写挂了 可能心态崩了就是从那场t1t1t1签到题考高精度数位…...

【数据结构】时间复杂度
🚀write in front🚀 📜所属专栏:初阶数据结构 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论,是对…...

vector的基本使用
目录 介绍: vector iterator 的使用 增删查改 增(push_back insert): 删(pop_back erase): swap: vector的容量和扩容: 排序(sort): 介绍ÿ…...

剑指 Offer 55 - I. 二叉树的深度
摘要 剑指 Offer 55 - I. 二叉树的深度 一、深度优先搜索 如果我们知道了左子树和右子树的最大深度l和r,那么该二叉树的最大深度即为:max(l,r)1。 而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计…...
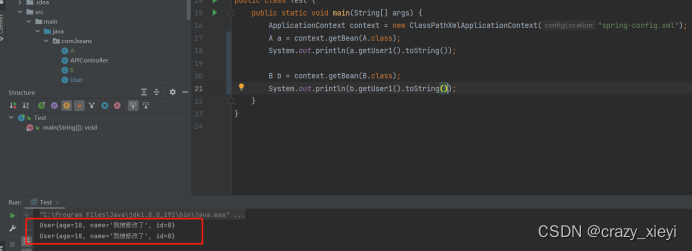
Bean的生命周期和作用域
Bean的生命周期Bean的执行流程:Bean 执行流程:启动Spring 容器 -> 实例化 Bean(分配内存空间,从无到有)-> Bean 注册到 Spring 中(存操作) -> 将 Bean 装配到需要的类中(取…...
TestNG和Junit的区别,测试框架该如何选择?
要想知道两个框架的区别,首先分别介绍一下两个框架。 TestNG是一个java中的开源自动化测试框架,其灵感来自JUnit和NUnit,TestNG还涵盖了JUnit4整个核心的功能,但引入了一些新的功能,使其功能更强大,使用更…...

MySQL安全登录策略
MySQL密码复杂度策略设置 MySQL 系统自带有 validate_password 插件,此插件可以验证密码强度,未达到规定强度的密码则不允许被设置。MySQL 5.7 及 8.0 版本默认情况下貌似都不启用该插件,这也使得我们可以随意设置密码,比如设置为…...

优化模型验证23:带无人机停靠站的卡车无人机协同配送车辆路径问题、模型、gurobipy验证及结果可视化
带中转hub的卡车无人机车辆路径问题 模型来源为:Wang Z , Sheu J B . Vehicle routing problem with drones[J]. Transportation Research Part B: Methodological, 2019, 122(APR.):350-364. 问题描述: 这篇问题研究了一个带停靠站的卡车无人机路径问题,无人机仅能从起点…...

mongoTemplate Aggregation 多表联查 排序失效问题解决
目录说明说明 接着上一个文章的例子来说:mongoTemplate支持多表联查 排序 条件筛选 分页 去重分组 在按照上一个demo的代码执行后,可能会发生排序失效的问题,为什么说可能呢?每个人负责业务不同,不可能是最简单的dem…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
