AOJ 0531 坐标离散化
一、题目大意
在(0<=x<=w,0<=y<=h)的坐标系里有多个矩形,把区域分成了多个部分,我们需要针对找出被矩形分割的连通的区块数量。
二、解题思路
这个题目其实和学DFS时候那个找出连通的水洼是一样的。只是这个地图比较大,没办法建立那么大的数组,但是矩形的数量也很少,所以考虑使用坐标离散化。
坐标离散化的思路其实也很简单,就是我们把每一个有效坐标k和它 的前一个k-1和后一个坐标k+1都放在一个数组里,然后对这个数组排序加去重(先排序再双指针去重最快),之后用元素k在这个数组里的位置来替换这个元素本身的值,这种离散化对于需要打表的题,比如DP、DFS、BFS比较有效。
本题目给出的是坐标,但是DFS需要用的是区块,所以我就把(x1,y1)到(x2,y2)的矩形看作从[x1,x2-1]到[y1,y2-1]这些坐标中间的区块。那么[0,w-1]的坐标范围,其实真正的放置区块的数量就是[0,w-2]也就是w-1个区块,这个说的其实不清晰,我表达能力确实是太差了。主要的意思就是解释下为什么我把去重后的数量-1作为w和h,因为坐标和区块之间差一个,所以减少一个。
三、代码
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> P;
int x[6007], y[6007], xLen, yLen, w, h, x_1[1007], x_2[1007], y_1[1007], y_2[1007], n, ans;
int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0, -1};
bool field[6007][6007];
queue<P> que;
void input()
{ans = 0;scanf("%d", &n);for (int i = 0; i < n; i++){scanf("%d%d%d%d", &x_1[i], &y_1[i], &x_2[i], &y_2[i]);}
}
void compress()
{xLen = 0;for (int i = 0; i < n; i++){if (x_1[i] > 0){x[xLen++] = x_1[i] - 1;}x[xLen++] = x_1[i];if (x_1[i] < w){x[xLen++] = x_1[i] + 1;}if (x_2[i] > 0){x[xLen++] = x_2[i] - 1;}x[xLen++] = x_2[i];if (x_2[i] < w){x[xLen++] = x_2[i] + 1;}}yLen = 0;for (int i = 0; i < n; i++){if (y_1[i] > 0){y[yLen++] = y_1[i] - 1;}y[yLen++] = y_1[i];if (y_1[i] < h){y[yLen++] = y_1[i] + 1;}if (y_2[i] > 0){y[yLen++] = y_2[i] - 1;}y[yLen++] = y_2[i];if (y_2[i] < h){y[yLen++] = y_2[i] + 1;}}sort(x, x + xLen);sort(y, y + yLen);
}
void distinctBy2Posinter()
{int tmpLen = 1;for (int i = 1; i < xLen; i++){if (x[tmpLen - 1] != x[i]){x[tmpLen++] = x[i];}}xLen = tmpLen;tmpLen = 1;for (int i = 1; i < yLen; i++){if (y[tmpLen - 1] != y[i]){y[tmpLen++] = y[i];}}yLen = tmpLen;
}
void handleX_1X_2Y_1Y_2()
{for (int i = 0; i < n; i++){x_1[i] = lower_bound(x, x + xLen, x_1[i]) - x;x_2[i] = lower_bound(x, x + xLen, x_2[i]) - x;y_1[i] = lower_bound(y, y + yLen, y_1[i]) - y;y_2[i] = lower_bound(y, y + yLen, y_2[i]) - y;}w = xLen - 1;h = yLen - 1;
}
void handleField()
{for (int i = 0; i < h; i++){for (int j = 0; j < w; j++){field[i][j] = true;}}for (int i = 0; i < n; i++){for (int j = y_1[i]; j <= (y_2[i] - 1); j++){for (int k = x_1[i]; k <= (x_2[i] - 1); k++){field[j][k] = false;}}}
}
void bfs()
{while (!que.empty()){P p = que.front();que.pop();for (int i = 0; i < 4; i++){int ny = p.first + dy[i];int nx = p.second + dx[i];if (ny >= 0 && ny < h && nx >= 0 && nx < w && field[ny][nx]){field[ny][nx] = false;que.push(P(ny, nx));}}}
}
void solve()
{for (int i = 0; i < h; i++){for (int j = 0; j < w; j++){if (field[i][j]){field[i][j] = false;que.push(P(i, j));bfs();ans++;}}}
}
int main()
{while (true){scanf("%d%d", &w, &h);if (w == 0 && h == 0){break;}input();compress();distinctBy2Posinter();handleX_1X_2Y_1Y_2();handleField();solve();printf("%d\n", ans);}return 0;
}相关文章:

AOJ 0531 坐标离散化
一、题目大意 在(0<x<w,0<y<h)的坐标系里有多个矩形,把区域分成了多个部分,我们需要针对找出被矩形分割的连通的区块数量。 二、解题思路 这个题目其实和学DFS时候那个找出连通的水洼是一样的。只是这个地图比较大,…...
Python —— pytest框架
1、认识pytest框架 1、搭建自动化框架的思路与流程 1、搭建自动化测试框架的思路和流程,任意测试手段流程都是一致的:手工测试、自动化测试、工具测试 手工测试:熟悉业务 —— 写用例 —— 执行用例并记录结果 —— 生成测试报告自动化测试…...

IP地址欺骗的危害与后果
IP地址欺骗,也被称为IP地址伪装或IP地址欺诈,是一种网络攻击技术,旨在伪装或隐藏攻击者的真实IP地址。尽管这种技术可能有一些合法的用途,例如保护用户的隐私或绕过地理位置限制,但它也经常被恶意黑客用于不法行为。本…...
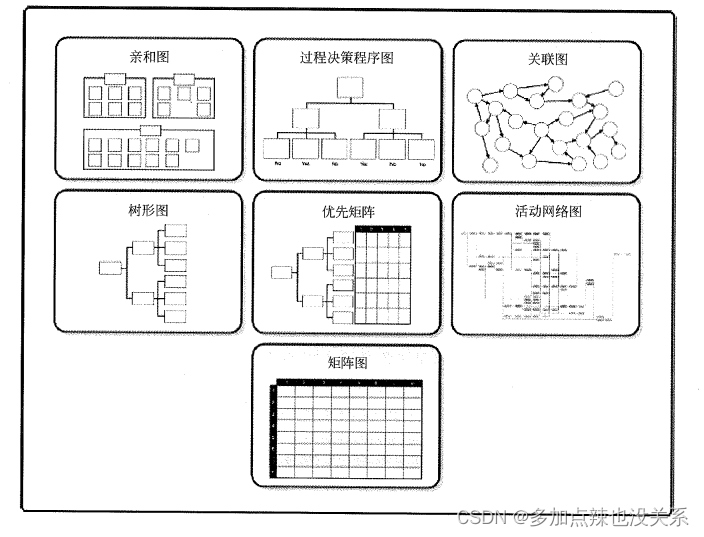
系统集成|第十章(笔记)
目录 第十章 质量管理10.1 项目质量管理概论10.2 主要过程10.2.1 规划质量管理10.2.2 实施质量保证10.2.3 质量控制 10.3 常见问题 上篇:第九章、成本管理 第十章 质量管理 10.1 项目质量管理概论 质量管理:指确定质量方针,质量目标和职责&a…...
配置)
Linux之perf(7)配置
Linux之perf(7)配置类命令 Author:Onceday Date:2023年9月23日 漫漫长路,才刚刚开始… 注:该文档内容采用了GPT4.0生成的回答,部分文本准确率可能存在问题。 参考文档: Tutorial - Perf Wiki (kernel.org)perf(1)…...
14:00面试,14:06就出来了,问的问题过于变态了。。。
从小厂出来,没想到在另一家公司又寄了。 到这家公司开始上班,加班是每天必不可少的,看在钱给的比较多的份上,就不太计较了。没想到5月一纸通知,所有人不准加班,加班费不仅没有了,薪资还要降40%…...
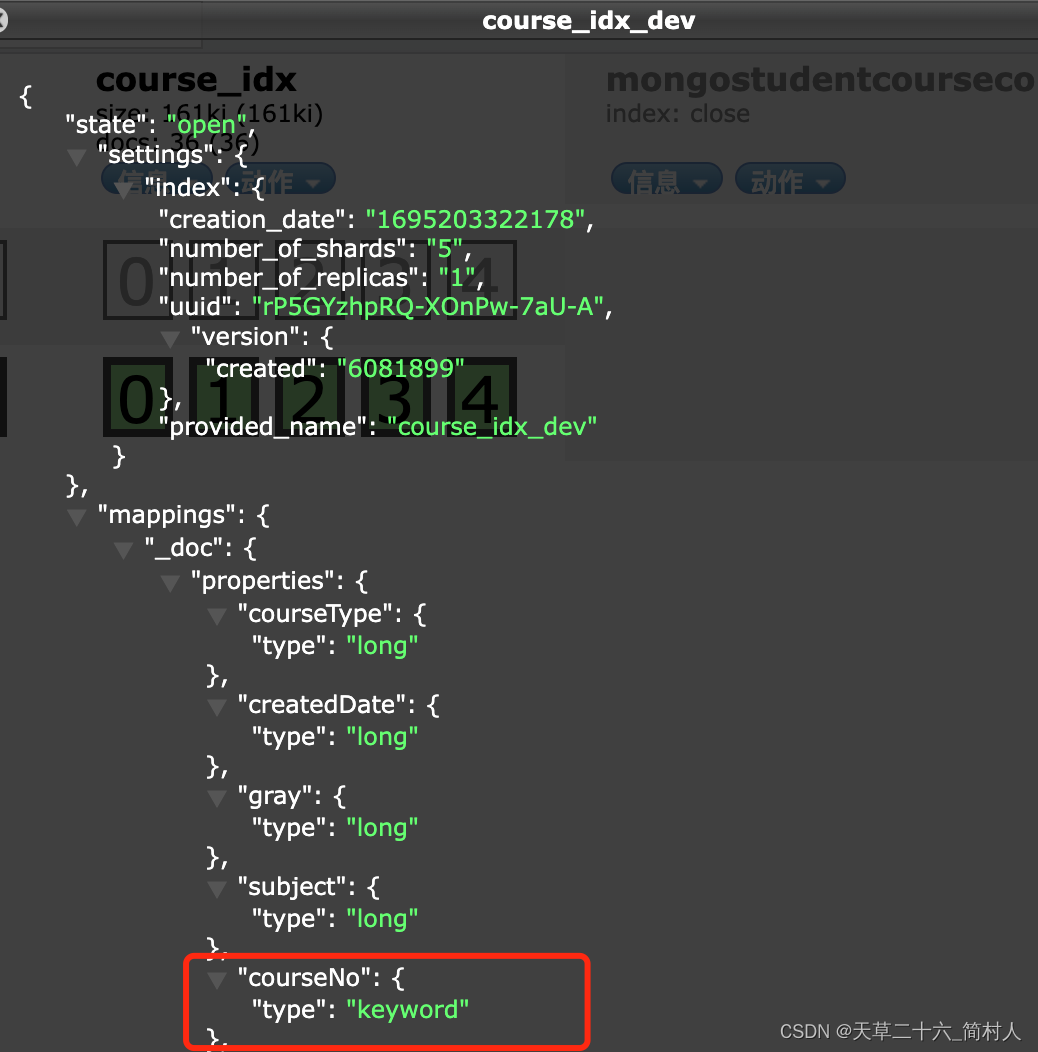
JPA的注解@Field指定为Keyword失败,导致查询不到数据
一、背景 使用 jpa 对es操作,查询条件不生效,需求是批量查询课程编号。说白了,就是一个In集合的查询。在es里,如果是精准匹配是termQuery,比如: queryBuilder.filter(QueryBuilders.termQuery(“schoolId…...

多线程带来的的风险-线程安全
多线程带来的的风险-线程安全 ~~ 多线程编程中,最难的地方,也是一个最重要的地方,还是一个最容易出错的地方,更是一个面试中特别爱考的地方.❤️❤️❤️ 线程安全的概念 万恶之源,罪魁祸首是多线程的抢占式执行,带来的随机性.~~😕😕&…...

Kafka 面试题
Kafka 面试题 Q:讲一下Kafka。 Kafka 入门一篇文章就够了 Kafka的简单理解 Q:消息队列,有哪些使用场景及用途? 解耦,削峰,限流。 Q:Kafka相对其他消息队列,有什么特点? 持久化:Kafka的持久化…...
离线部署 python 3.x 版本
文章目录 离线部署 python 3.x 版本1. 下载版本2. 上传到服务器3. 解压并安装4. 新建软连信息5. 注意事项 离线部署 python 3.x 版本 1. 下载版本 python 各版本下载地址 本次使用版本 Python-3.7.0a2.tgz # linux 可使用 wget 下载之后上传到所需服务器 wget https://www.py…...

Java 获取豆瓣电影TOP250
对于爬虫,Java并不是最擅长的,但是也可以实现,此次主要用到的包有hutool和jsoup。 hutool是一个Java工具包,它简化了Java的各种API操作,包括文件操作、类型转换、HTTP、日期处理、JSON处理、加密解密等。它的目标是使…...
)
笔试面试相关记录(5)
(1)不包含重复字符的最长子串的长度 #include <iostream> #include <string> #include <map>using namespace std;int getMaxLength(string& s) {int len s.size();map<char, int> mp;int max_len 0;int left 0;int i …...
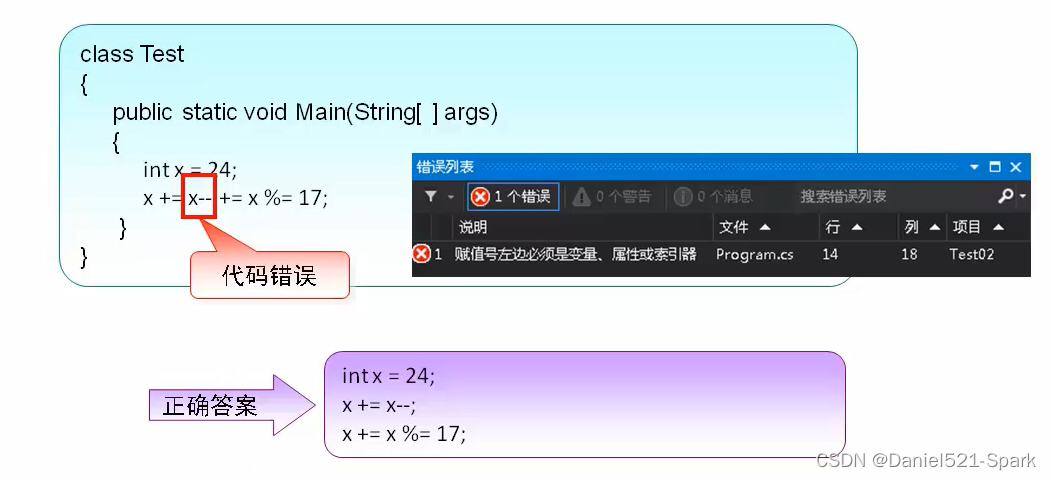
四、C#—变量,表达式,运算符(2)
🌻🌻 目录 一、表达式1.1 什么是表达式1.2 表达式的基本组成 二、运算符2.1 算术运算符2.1.1 使用 / 运算符时的注意事项2.1.2 使用%运算符时的注意事项 2.2 赋值运算符2.2.1 简单赋值运算符2.2.2 复合赋值运算符 2.3 关系运算符2.4 逻辑运算符2.4.1 逻辑…...
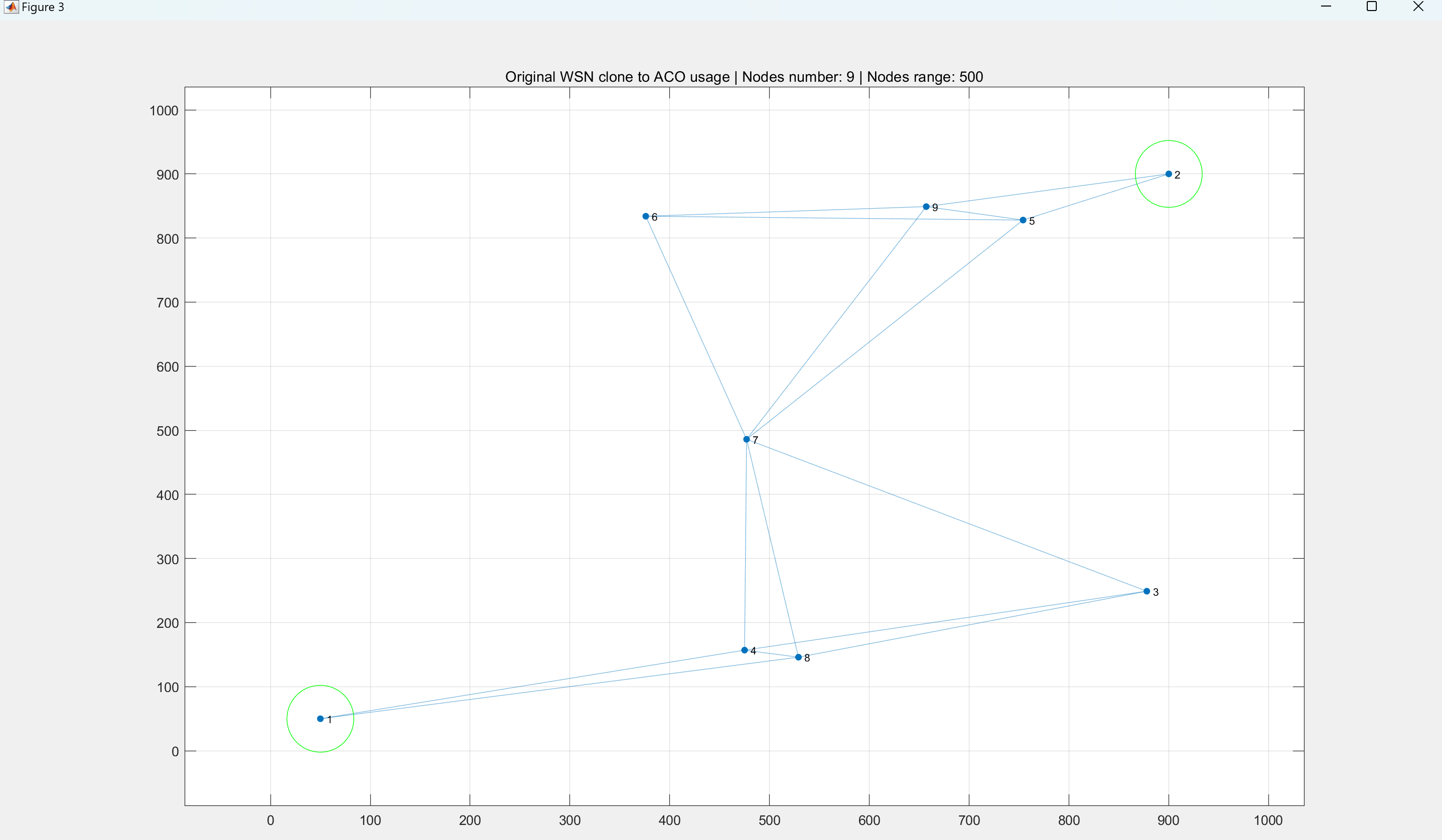
【WSN】基于蚁群算法的WSN路由协议(最短路径)消耗节点能量研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
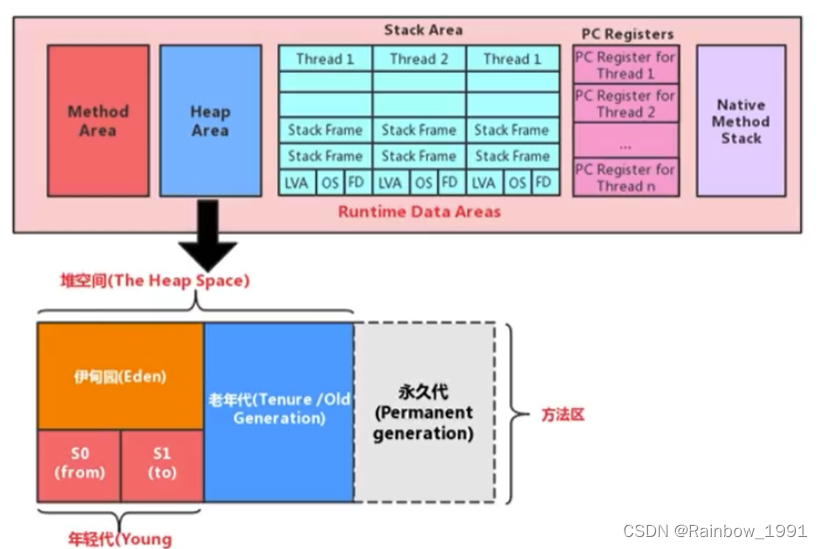
JVM的内存分配及垃圾回收
内存分配 在了解Java的内存管理前,需要知道JVM中的内存分配。 栈 存储局部变量。在方法的定义中或在方法中声明的变量为局部变量;栈内存中的数据在该方法结束(返回或抛出异常或方法体运行到最后)时自动释放栈中存放的数据结构为…...

Python实现查询一个文件中的pdf文件中的关键字
要求,查询一个文件中的pdf文件中的关键字,输出关键字所在PDF文件的文件名及对应的页数。 import os import PyPDF2def search_pdf_files(folder_path, keywords):# 初始化结果字典,以关键字为键,值为包含关键字的页面和文件名列表…...

【计算机网络笔记一】网络体系结构
IP和路由器概念 两台主机如何通信呢? 首先,主机的每个网卡都有一个全球唯一地址,MAC 地址,如 00:10:5A:70:33:61 查看 MAC 地址: windows: ipconfig / alllinux:ifconfig 或者 ip addr 同一个网络的多…...

硕士应聘大专老师
招聘信息 当地人社局、学校(官方) 公众号(推荐): 辅导员招聘 厦门人才就业信息平台 高校人才网V 公告出完没多久就要考试面试,提前联系当地院校,问是否招人。 校招南方某些学校会直接去招老师。…...

Gram矩阵
Gram矩阵如何计算 Gram 矩阵是由一组向量的内积构成的矩阵。如果你有一组向量 v 1 , v 2 , … , v n v_1, v_2, \ldots, v_n v1,v2,…,vn,Gram 矩阵 G G G 的元素 G i j G_{ij} Gij 就是向量 v i v_i vi 和向量 v j v_j vj 的内积。数学上&#x…...
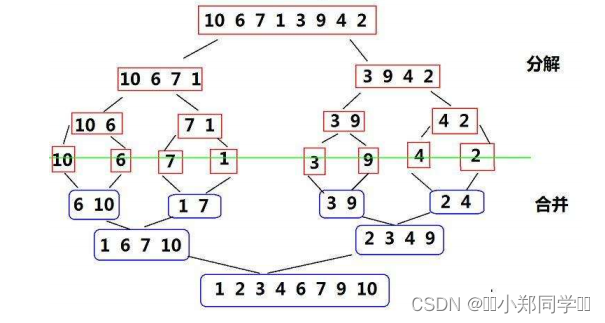
【数据结构】七大排序算法详解
目录 ♫什么是排序 ♪排序的概念 ♪排序的稳定性 ♪排序的分类 ♪常见的排序算法 ♫直接插入排序 ♪基本思想 ♪算法实现 ♪算法稳定性 ♪时间复杂度 ♪空间复杂度 ♫希尔排序 ♪基本思想 ♪算法实现 ♪算法稳定性 ♪时间复杂度 ♪空间复杂度 ♫直接选择排序 ♪基本思想 ♪算法…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
