当前位置： 首页 > news >正文

Python 安装js环境

news 2026/2/10 23:26:59

 在终端执行下面的命令

npm install jsdom

jsdom 是一个实现了 DOM API 的 JavaScript 环境，用于在 Node.js 中模拟浏览器的 DOM 环境。execjs 使用 jsdom 这个模块来执行 JavaScript 代码。所以在你的系统中，需要先安装并配置好 jsdom 模块，才能正常使用 execjs 

安装PyExecJS

只有安装了PyExecJS才能import

pip install PyExecJSimport execjs

新建js文件

在开头写补环境

const jsdom = require("jsdom");
const {JSDOM} = jsdom;
const dom = new JSDOM(`<!DOCTYPE html><p>Hello world</p>`);
window = dom.window;
document = window.document;
XMLHttpRequest = window.XMLHttpRequest;

然后再写自己的代码即可

此时即可运行js代码

    with open("js文件所在路径", encoding='utf-8', mode='r') as f:js_code = f.read()ctx = execjs.compile(js_code)

相关文章：

Python 安装js环境

在终端执行下面的命令 npm install jsdom jsdom 是一个实现了 DOM API 的 JavaScript 环境&#xff0c;用于在 Node.js 中模拟浏览器的 DOM 环境。execjs 使用 jsdom 这个模块来执行 JavaScript 代码。所以在你的系统中&#xff0c;需要先安装并配置好 jsdom 模块&#xff0c…...

编程日记 2023/9/24 11:09:48

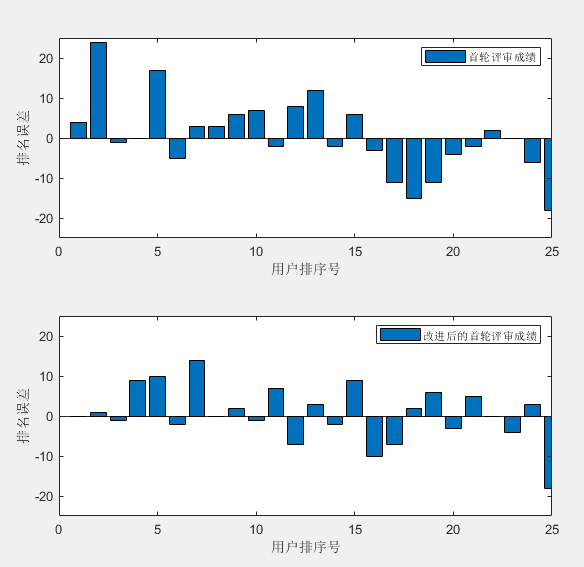
2023华为杯数模C题——大规模创新类竞赛评审方案研究

B题——大规模创新类竞赛评审方案研究 思路&#xff1a;采用数据分析等手段改进评分算法性能 完成情况(1-2问已经完成) 代码下载 问题一 在每个评审阶段&#xff0c;作品通常都是随机分发的&#xff0c;每份作品需要多位评委独立评审。为了增加不同评审专家所给成绩之间的可比…...

编程日记 2023/9/24 11:08:46

人工神经网络ANN：数学总结

一、内容 径向基函数&#xff08;Radial basis function&#xff0c;RBF&#xff09;&#xff1a;一个取值仅依赖于到原点距离的实值函数&#xff0c;即。此外&#xff0c;也可以按到某一中心点c的距离来定义&#xff0c;即。 可以用于许多向函基数的和来逼近某一给定的函数&a…...

编程日记 2023/9/24 11:06:45

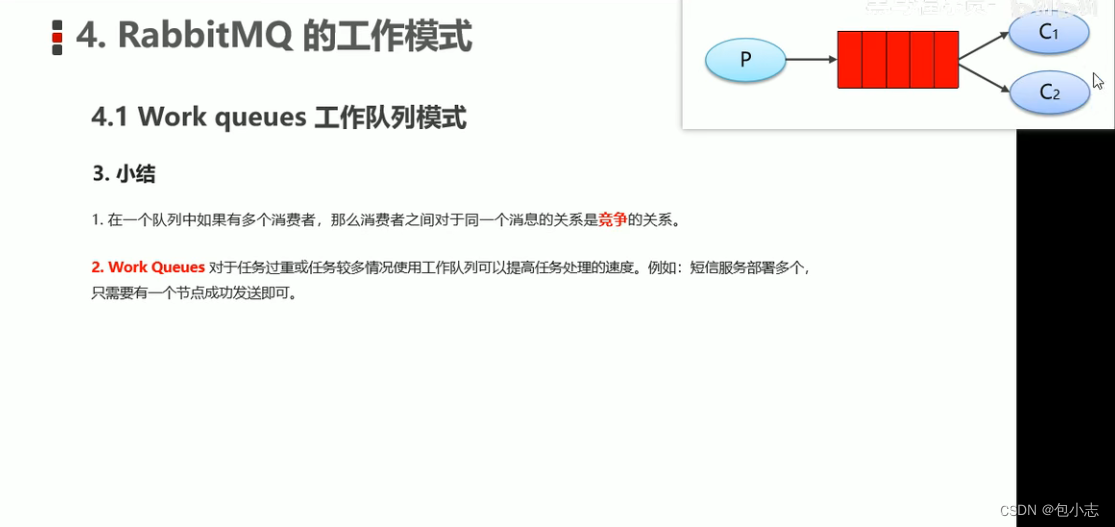
RabbitMQ的工作模式——WorkQueues

1.工作队列模式 生产者代码 public class Producer_WorkQueues1 {public static void main(String[] args) throws IOException, TimeoutException {//1.创建连接工厂ConnectionFactory factory new ConnectionFactory();//2.设置参数factory.setHost("172.16.98.133&qu…...

编程日记 2023/9/24 11:04:42

AOJ 0531 坐标离散化

一、题目大意 在(0<x<w&#xff0c;0<y<h)的坐标系里有多个矩形&#xff0c;把区域分成了多个部分&#xff0c;我们需要针对找出被矩形分割的连通的区块数量。 二、解题思路 这个题目其实和学DFS时候那个找出连通的水洼是一样的。只是这个地图比较大&#xff0c…...

编程日记 2023/9/24 11:01:39

Python —— pytest框架

1、认识pytest框架 1、搭建自动化框架的思路与流程 1、搭建自动化测试框架的思路和流程&#xff0c;任意测试手段流程都是一致的&#xff1a;手工测试、自动化测试、工具测试 手工测试&#xff1a;熟悉业务 —— 写用例 —— 执行用例并记录结果 —— 生成测试报告自动化测试…...

编程日记 2023/9/24 10:59:33

IP地址欺骗的危害与后果

IP地址欺骗&#xff0c;也被称为IP地址伪装或IP地址欺诈&#xff0c;是一种网络攻击技术&#xff0c;旨在伪装或隐藏攻击者的真实IP地址。尽管这种技术可能有一些合法的用途&#xff0c;例如保护用户的隐私或绕过地理位置限制&#xff0c;但它也经常被恶意黑客用于不法行为。本…...

编程日记 2023/9/24 10:58:31

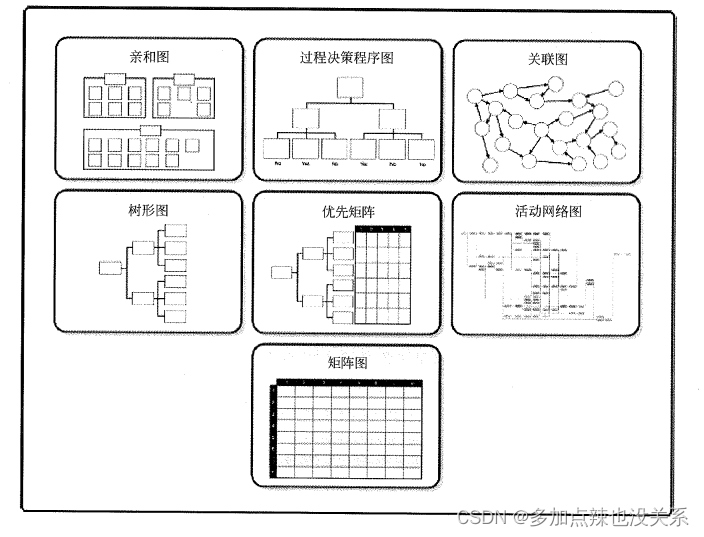
系统集成|第十章(笔记)

目录 第十章 质量管理10.1 项目质量管理概论10.2 主要过程10.2.1 规划质量管理10.2.2 实施质量保证10.2.3 质量控制 10.3 常见问题 上篇&#xff1a;第九章、成本管理 第十章 质量管理 10.1 项目质量管理概论 质量管理&#xff1a;指确定质量方针&#xff0c;质量目标和职责&a…...

编程日记 2023/9/24 10:57:30

Linux之perf(7)配置

Linux之perf(7)配置类命令 Author&#xff1a;Onceday Date&#xff1a;2023年9月23日 漫漫长路&#xff0c;才刚刚开始… 注&#xff1a;该文档内容采用了GPT4.0生成的回答&#xff0c;部分文本准确率可能存在问题。 参考文档: Tutorial - Perf Wiki (kernel.org)perf(1)…...

编程日记 2023/9/24 10:56:28

14：00面试，14：06就出来了，问的问题过于变态了。。。

从小厂出来&#xff0c;没想到在另一家公司又寄了。 到这家公司开始上班&#xff0c;加班是每天必不可少的&#xff0c;看在钱给的比较多的份上&#xff0c;就不太计较了。没想到5月一纸通知&#xff0c;所有人不准加班&#xff0c;加班费不仅没有了&#xff0c;薪资还要降40%…...

编程日记 2023/9/24 10:55:27

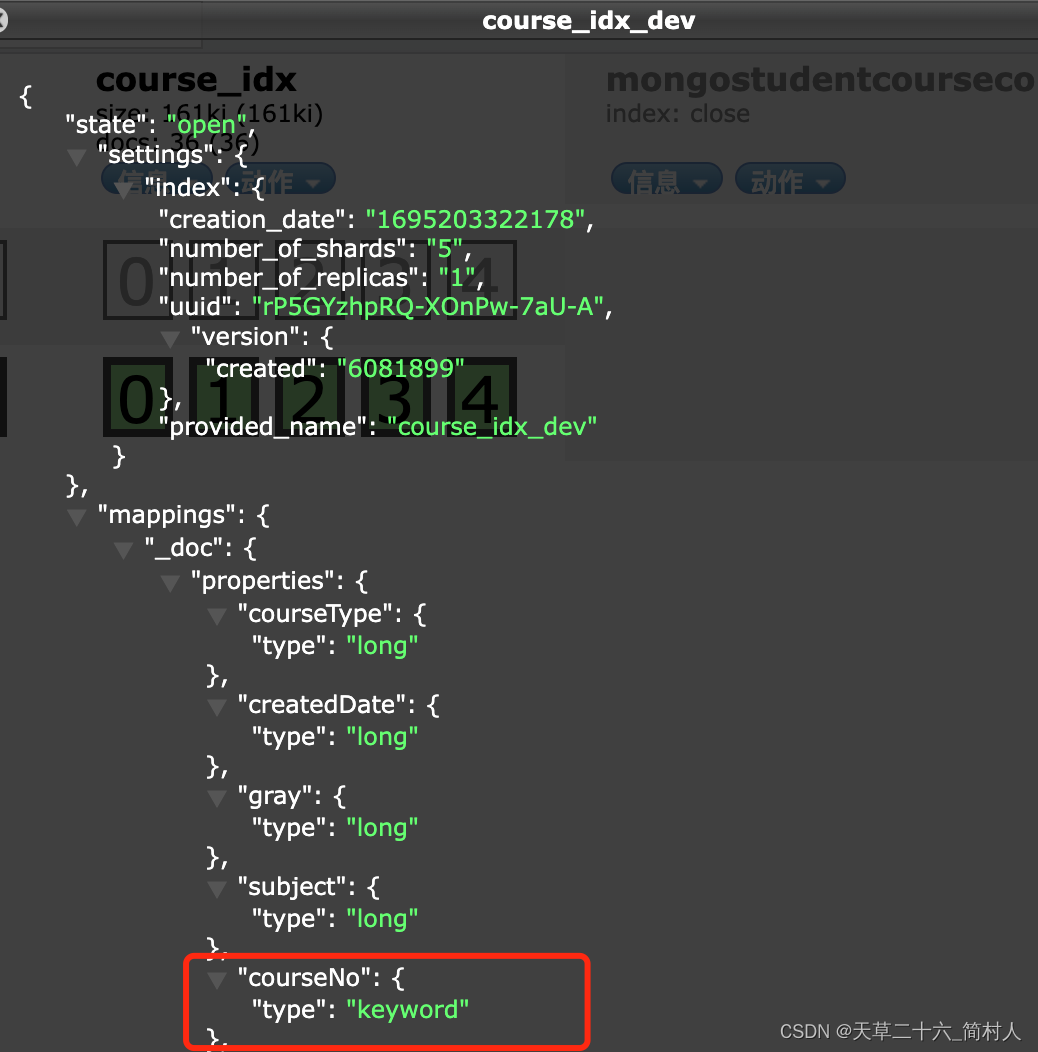
JPA的注解@Field指定为Keyword失败，导致查询不到数据

一、背景 使用 jpa 对es操作&#xff0c;查询条件不生效&#xff0c;需求是批量查询课程编号。说白了&#xff0c;就是一个In集合的查询。在es里&#xff0c;如果是精准匹配是termQuery&#xff0c;比如&#xff1a; queryBuilder.filter(QueryBuilders.termQuery(“schoolId…...

编程日记 2023/9/24 10:52:22

多线程带来的的风险-线程安全

多线程带来的的风险-线程安全 ~~ 多线程编程中,最难的地方,也是一个最重要的地方&#xff0c;还是一个最容易出错的地方,更是一个面试中特别爱考的地方.❤️❤️❤️ 线程安全的概念 万恶之源,罪魁祸首是多线程的抢占式执行,带来的随机性.~~&#x1f615;&#x1f615;&…...

编程日记 2023/9/24 10:46:15

Kafka 面试题

Kafka 面试题 Q:讲一下Kafka。 Kafka 入门一篇文章就够了 Kafka的简单理解 Q:消息队列&#xff0c;有哪些使用场景及用途&#xff1f; 解耦&#xff0c;削峰&#xff0c;限流。 Q:Kafka相对其他消息队列&#xff0c;有什么特点&#xff1f; 持久化&#xff1a;Kafka的持久化…...

编程日记 2023/9/24 10:45:14

离线部署 python 3.x 版本

文章目录 离线部署 python 3.x 版本1. 下载版本2. 上传到服务器3. 解压并安装4. 新建软连信息5. 注意事项 离线部署 python 3.x 版本 1. 下载版本 python 各版本下载地址 本次使用版本 Python-3.7.0a2.tgz # linux 可使用 wget 下载之后上传到所需服务器 wget https://www.py…...

编程日记 2023/9/24 10:44:12

Java 获取豆瓣电影TOP250

对于爬虫&#xff0c;Java并不是最擅长的&#xff0c;但是也可以实现&#xff0c;此次主要用到的包有hutool和jsoup。 hutool是一个Java工具包&#xff0c;它简化了Java的各种API操作&#xff0c;包括文件操作、类型转换、HTTP、日期处理、JSON处理、加密解密等。它的目标是使…...

编程日记 2023/9/24 10:43:11

笔试面试相关记录（5）

&#xff08;1&#xff09;不包含重复字符的最长子串的长度 #include <iostream> #include <string> #include <map>using namespace std;int getMaxLength(string& s) {int len s.size();map<char, int> mp;int max_len 0;int left 0;int i …...

编程日记 2023/9/24 10:42:09

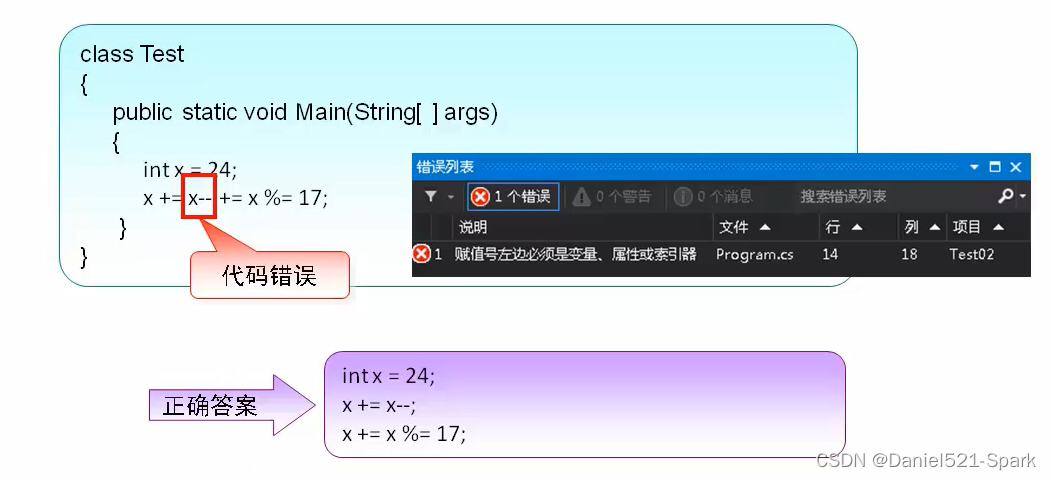
四、C#—变量，表达式，运算符（2）

&#x1f33b;&#x1f33b; 目录 一、表达式1.1 什么是表达式1.2 表达式的基本组成 二、运算符2.1 算术运算符2.1.1 使用 / 运算符时的注意事项2.1.2 使用%运算符时的注意事项 2.2 赋值运算符2.2.1 简单赋值运算符2.2.2 复合赋值运算符 2.3 关系运算符2.4 逻辑运算符2.4.1 逻辑…...

编程日记 2023/9/24 10:40:07

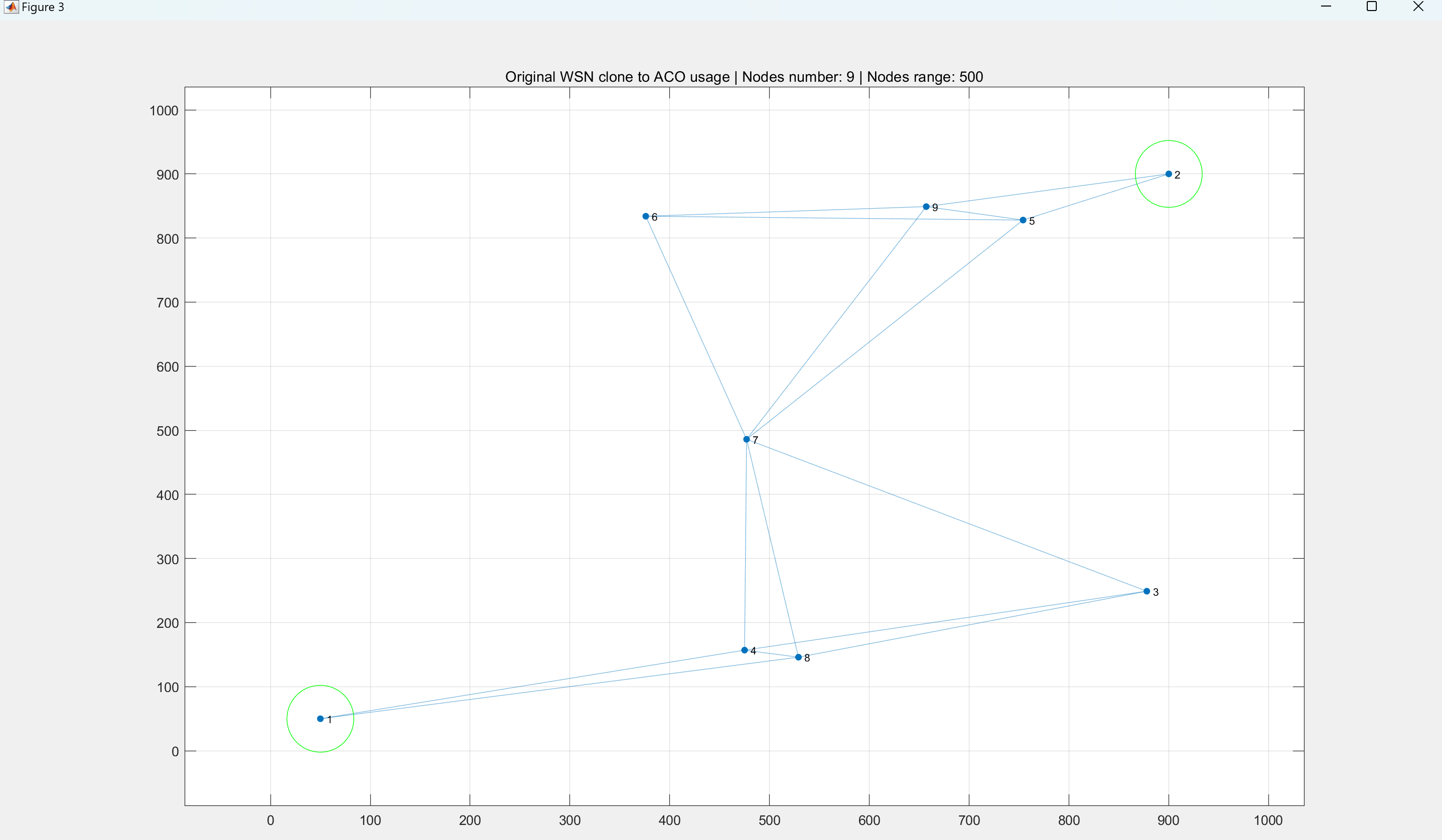
【WSN】基于蚁群算法的WSN路由协议(最短路径)消耗节点能量研究（Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…...

编程日记 2023/9/24 10:39:05

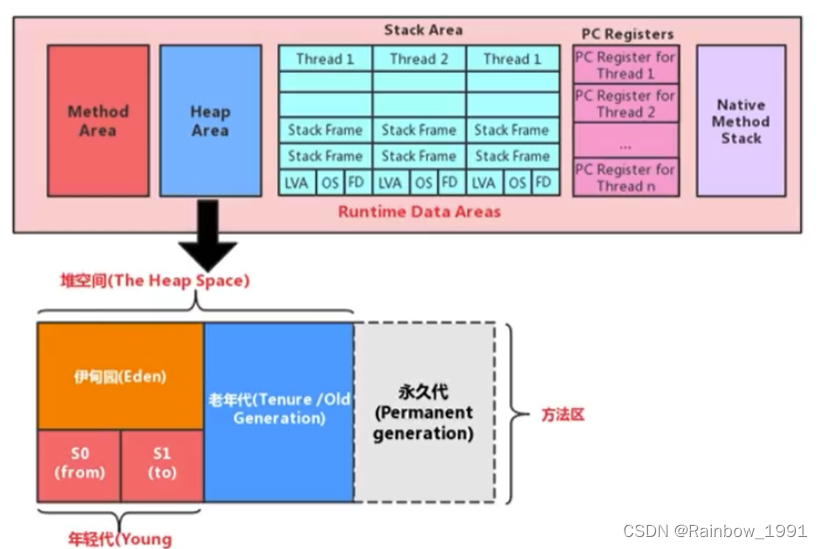
JVM的内存分配及垃圾回收

内存分配 在了解Java的内存管理前&#xff0c;需要知道JVM中的内存分配。 栈 存储局部变量。在方法的定义中或在方法中声明的变量为局部变量&#xff1b;栈内存中的数据在该方法结束&#xff08;返回或抛出异常或方法体运行到最后&#xff09;时自动释放栈中存放的数据结构为…...

编程日记 2023/9/24 10:38:04

Python实现查询一个文件中的pdf文件中的关键字

要求&#xff0c;查询一个文件中的pdf文件中的关键字&#xff0c;输出关键字所在PDF文件的文件名及对应的页数。 import os import PyPDF2def search_pdf_files(folder_path, keywords):# 初始化结果字典&#xff0c;以关键字为键&#xff0c;值为包含关键字的页面和文件名列表…...

编程日记 2023/9/24 10:37:02

2024年赣州旅游投资集团社会招聘笔试真

2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案，答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年，()预言了电磁波的存在，并指出…...

编程新知 2025/12/10 4:08:53

cf2117E

原题链接&#xff1a;https://codeforces.com/contest/2117/problem/E 题目背景&#xff1a; 给定两个数组a,b&#xff0c;可以执行多次以下操作&#xff1a;选择 i (1 < i < n - 1)&#xff0c;并设置 或&#xff0c;也可以在执行上述操作前执行一次删除任意 和 。求…...

编程新知 2026/2/10 15:49:16

学习STC51单片机32（芯片为STC89C52RCRC）OLED显示屏2

每日一言 今天的每一份坚持&#xff0c;都是在为未来积攒底气。 案例&#xff1a;OLED显示一个A 这边观察到一个点&#xff0c;怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 &#xff1a; 如果代码里信号切换太快&#xff08;比如 SDA 刚变&#xff0c;SCL 立刻变&#…...

编程新知 2026/2/6 0:50:24

深度学习水论文：mamba＋图像增强

&#x1f9c0;当前视觉领域对高效长序列建模需求激增&#xff0c;对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模&#xff0c;以及动态计算优势&#xff0c;在图像质量提升和细节恢复方面有难以替代的作用。 &#x1f9c0;因此短时间内&#xff0c;就有不…...

编程新知 2026/1/26 4:52:47

C# 表达式和运算符(求值顺序)

求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如&#xff0c;已知表达式3*52&#xff0c;依照子表达式的求值顺序&#xff0c;有两种可能的结果&#xff0c;如图9-3所示。 如果乘法先执行&#xff0c;结果是17。如果5…...

编程新知 2026/1/31 13:13:28

破解路内监管盲区：免布线低位视频桩重塑停车管理新标准

城市路内停车管理常因行道树遮挡、高位设备盲区等问题&#xff0c;导致车牌识别率低、逃费率高&#xff0c;传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法&#xff0c;正成为破局关键。该设备安装于车位侧方0.5-0.7米高度&#xff0c;直接规避树枝遮…...

编程新知 2026/2/1 15:29:27

springboot 日志类切面，接口成功记录日志，失败不记录

springboot 日志类切面&#xff0c;接口成功记录日志&#xff0c;失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

编程新知 2026/2/1 13:59:09

沙箱虚拟化技术虚拟机容器之间的关系详解

问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西&#xff0c;但是如果把三者放在一起&#xff0c;它们之间到底什么关系&#xff1f;又有什么联系呢&#xff1f;我不是很明白&#xff01;&#xff01;&#xff01; 就比如说&#xff1a; 沙箱&#…...

编程新知 2026/2/6 6:05:52

CSS 工具对比：UnoCSS vs Tailwind CSS，谁是你的菜？

在现代前端开发中&#xff0c;Utility-First (功能优先) CSS 框架已经成为主流。其中&#xff0c;Tailwind CSS 无疑是市场的领导者和标杆。然而&#xff0c;一个名为 UnoCSS 的新星正以其惊人的性能和极致的灵活性迅速崛起。 这篇文章将深入探讨这两款工具的核心理念、技术差…...

编程新知 2026/2/5 16:05:59

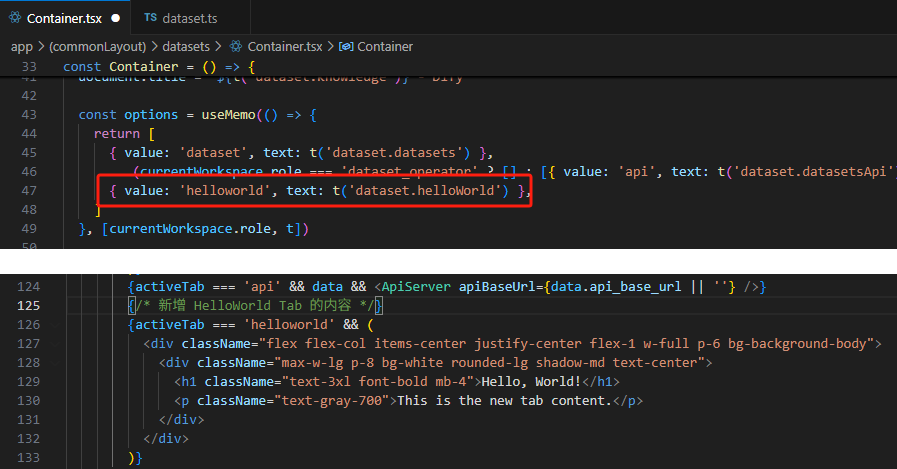
【技巧】dify前端源代码修改第一弹-增加tab页

回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码&#xff0c;在知识库增加一个tab页"HELLO WORLD"&#xff0c;完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...

编程新知 2026/2/8 9:41:45