pytorch学习---实现线性回归初体验
假设我们的基础模型就是y = wx + b,其中w和b均为参数,我们使用y = 3x+0.8来构造数据x、y,所以最后通过模型应该能够得出w和b应该分别接近3和0.8。
步骤如下:
- 准备数据
- 计算预测值
- 计算损失,把参数的梯度置为0,进行反向传播
- 更新参数
方式一
该方式没有用pytorch的模型api,手动实现
import torch,numpy
import matplotlib.pyplot as plt# 1、准备数据
learning_rate = 0.01
#y=3x + 0.8
x = torch.rand([500,1])
y_true= x*3 + 0.8# 2、通过模型计算y_predict
w = torch.rand([1,1],requires_grad=True)
b = torch.tensor(0,requires_grad=True,dtype=torch.float32)# 3、通过循环,反向传播,更新参数
for i in range(500):# 4、计算lossy_predict = torch.matmul(x,w) + bloss = (y_true-y_predict).pow(2).mean()# 每次循环判断是否存在梯度,防止累加if w.grad is not None:w.grad.data.zero_()if b.grad is not None:b.grad.data.zero_()# 反向传播loss.backward()w.data = w.data - learning_rate*w.gradb.data = b.data - learning_rate*b.grad# 每50次输出一下结果if i%50==0:print("w,b,loss",w.item(),b.item(),loss.item())#可视化显示
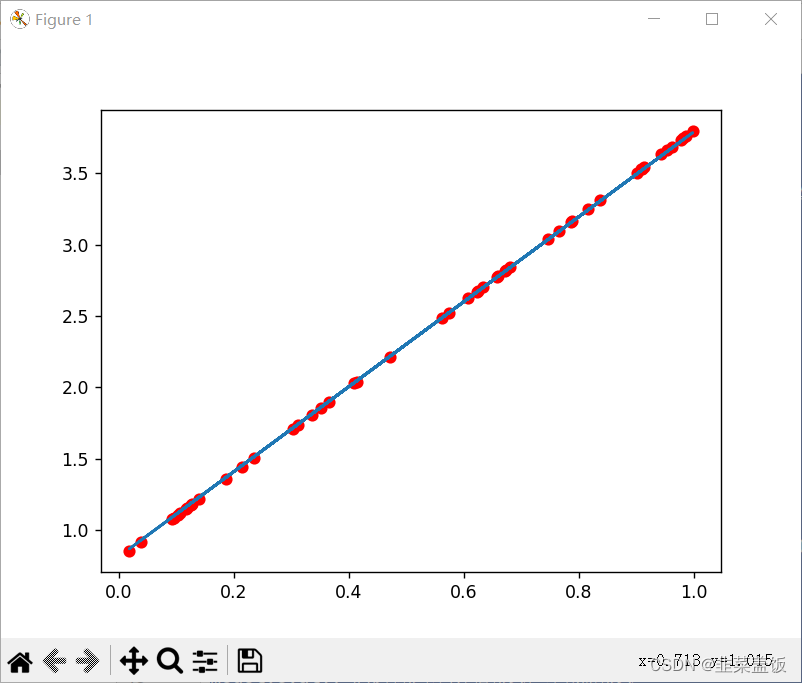
plt.figure(figsize=(20,8))
plt.scatter(x.numpy().reshape(-1),y_true.numpy().reshape(-1))
y_predict = torch.matmul(x,w) + b
plt.plot(x.numpy().reshape(-1),y_predict.detach().numpy().reshape(-1),c="r")
plt.show()循环500次的效果

循环2000次的结果

方式二
方式一的方式虽然已经购简便了,但是还是有些许繁琐,所以我们可以采用pytorch的api来实现。
nn.Module是torch.nn提供的一个类,是pytorch中我们自定义网络的一个基类,在这个类中定义了很多有用的方法,让我们在继承这个类定义网络的时候非常简单。
当我们自定义网络的时候,有两个方法需要特别注意:
1.__init__需要调用super方法,继承父类的属性和方法
2. forward方法必须实现,用来定义我们的网络的向前计算的过程用前面的y = wx+b的模型举例如下:
#定义模型
from torch import nn
class Lr(nn.Module): #继承nn.Moduledef __init__(self):super(Lr, self).__init__()self.linear = nn.Linear(1,1)def forward(self,x):out = self.linear(x)return out
全部代码如下:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import torch
from torch import nn
from torch import optim
import numpy as np
from matplotlib import pyplot as plt#1、定义数据
x = torch.rand([50,1])
y = x*3 + 0.8#定义模型
class Lr(nn.Module): #继承nn.Moduledef __init__(self):super(Lr, self).__init__()self.linear = nn.Linear(1,1)def forward(self,x):out = self.linear(x)return out
#2、实例化模型、loss函数以及优化器
model = Lr()
criterion = nn.MSELoss() #损失函数
optimizer = optim.SGD(model.parameters(),lr=1e-3) #优化器#3、训练模型
for i in range(3000):out = model(x)# 获取预测值loss = criterion(y,out) #计算损失optimizer.zero_grad() #梯度归零loss.backward() #计算梯度optimizer.step() #更新梯度if(i+1) % 20 ==0:print('Epoch[{}/{}],loss:{:.6f}'.format(i,500,loss.data))#4、模型评估
model.eval() #设置模型为评估模式,即预测模式
predict = model(x)
predict = predict.data.numpy()
plt.scatter(x.data.numpy(),y.data.numpy(),c="r")
plt.plot(x.data.numpy(),predict)
plt.show()注意:
model.eval()表示设置模型为评估模式,即预测模式
model.train(mode=True) 表示设置模型为训练模式
在当前的线性回归中,上述并无区别
但是在其他的一些模型中,训练的参数和预测的参数会不相同,到时候就需要具体告诉程序我们是在进行训练还是预测,比如模型中存在Dropout,BatchNorm的时候
循环2000次的结果:

循环30000次的结果:
相关文章:

pytorch学习---实现线性回归初体验
假设我们的基础模型就是y wx b,其中w和b均为参数,我们使用y 3x0.8来构造数据x、y,所以最后通过模型应该能够得出w和b应该分别接近3和0.8。 步骤如下: 准备数据计算预测值计算损失,把参数的梯度置为0,进行反向传播…...

别再乱写git commit了
B站|公众号:啥都会一点的研究生 写在前面 在很长的一段时间中,使用git commit都是随心所欲,log肥肠简洁,随着代码的迭代,当时有多偷懒,返过头查看git日志就有多懊悔,就和写代码不写doc string…...

八大排序(一)冒泡排序,选择排序,插入排序,希尔排序
一、冒泡排序 冒泡排序的原理是:从左到右,相邻元素进行比较。每次比较一轮,就会找到序列中最大的一个或最小的一个。这个数就会从序列的最右边冒出来。 以从小到大排序为例,第一轮比较后,所有数中最大的那个数就会浮…...

泊松分布简要介绍
泊松分布是一种常见的离散概率分布,它用于描述某个时间段或区域内随机事件发生的次数。它得名于法国数学家西蒙丹尼泊松。 泊松分布的概率质量函数表示某个时间段或区域内事件发生次数的概率。如果随机变量 X 服从泊松分布,记作 X ~ Poisson(λ)&#x…...

C语言每日一题(10):无人生还
文章主题:无人生还🔥所属专栏:C语言每日一题📗作者简介:每天不定时更新C语言的小白一枚,记录分享自己每天的所思所想😄🎶个人主页:[₽]的个人主页🏄…...

VSCode开发go手记
断点调试: 安装delve(windows): go get -u github.com/go-delve/delve/cmd/dlv 设置 launch.json 配置文件: ctrlshiftp 输入 Debug: Open launch.json 打开 launch.json 文件,如果第一次打开,会新建一…...

怎么选择AI伪原创工具-AI伪原创工具有哪些
在数字时代,创作和发布内容已经成为了一种不可或缺的活动。不论您是个人博主、企业家还是网站管理员,都会面临一个共同的挑战:如何在互联网上脱颖而出,吸引更多的读者和访客。而正是在这个背景下,AI伪原创工具逐渐崭露…...

【块状链表C++】文本编辑器(指针中 引用 的使用)
》》》算法竞赛 /*** file * author jUicE_g2R(qq:3406291309)————彬(bin-必应)* 一个某双流一大学通信与信息专业大二在读 * * brief 一直在竞赛算法学习的路上* * copyright 2023.9* COPYRIGHT 原创技术笔记:转载…...
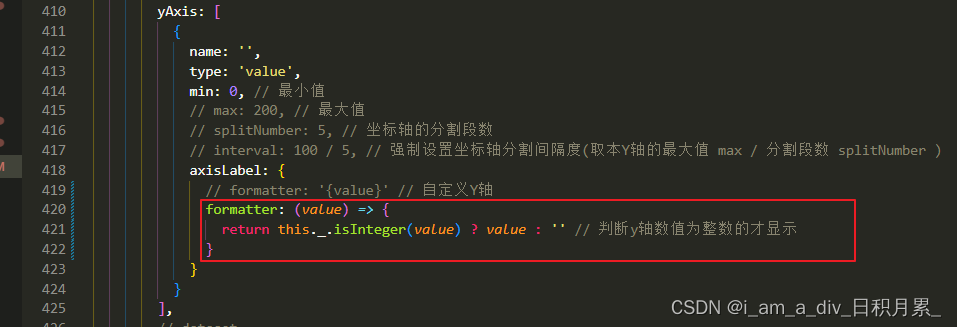
echarts的Y轴设置为整数
场景:使用echarts,设置Y轴为整数。通过判断Y轴的数值为整数才显示即可 yAxis: [{name: ,type: value,min: 0, // 最小值// max: 200, // 最大值// splitNumber: 5, // 坐标轴的分割段数// interval: 100 / 5, // 强制设置坐标轴分割间隔度(取本Y轴的最大…...
恢复删除文件?不得不掌握的4个方法!
“删除了的文件还可以恢复吗?有个文件我本来以为不重要了,就把它删除了,没想到现在还需要用到!这可怎么办?有没有办法找回来呢?” 重要的文件一旦丢失或误删可能都会对我们的工作和学习造成比较大的影响。怎…...

GitLab CI/CD:.gitlab-ci.yml 文件常用参数小结
文章目录 一、.gitlab-ci.yml 文件作用二、一个简单的.gitlab-ci.yml 文件示例参考 一、.gitlab-ci.yml 文件作用 可以定义跑CI时想要运行的命令或脚本 可以定义job之间的依赖和缓存 可以执行程序部署并定义部署位置 可以定义想要包含的其他配置文件和模版 二、一个简单的.gi…...
MySQL学习笔记9
MySQL数据表中的数据类型: 在考虑数据类型、长度、标度和精度时,一定要仔细地进行短期和长远的规划,另外,公司制度和希望用户用什么方式访问数据也是要考虑的因素。开发人员应该了解数据的本质,以及数据在数据库里是如…...

从零学习开发一个RISC-V操作系统(三)丨嵌入式操作系统开发的常用概念和工具
本篇文章的内容 一、嵌入式操作习系统开发的常用概念和工具1.1 本地编译和交叉编译1.2 调试器GDB(The GNU Project Debugger)1.3 QEMU模拟器1.4 项目构造工具Make 本系列是博主参考B站课程学习开发一个RISC-V的操作系统的学习笔记,计划从RISC…...
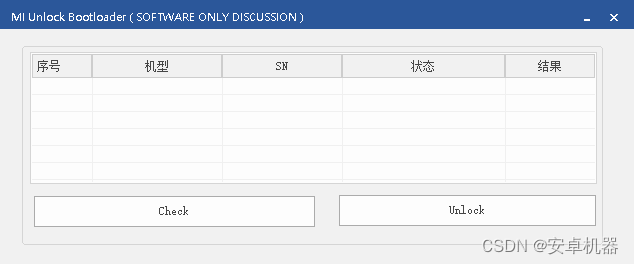
小米机型解锁bl 跳“168小时”限制 操作步骤分析
写到前面的安全提示 了解解锁bl后的风险: 解锁设备后将允许修改系统重要组件,并有可能在一定程度上导致设备受损;解锁后设备安全性将失去保证,易受恶意软件攻击,从而导致个人隐私数据泄露;解锁后部分对系…...

基础练习 回文数
问题描述 1221是一个非常特殊的数,它从左边读和从右边读是一样的,编程求所有这样的四位十进制数。 输出格式 按从小到大的顺序输出满足条件的四位十进制数。 solution1 #include <stdio.h> int main(){int n 1000, n1, n2, n3, n4;while(n &…...

解决Spring Boot 2.7.16 在服务器显示启动成功无法访问问题:从本地到服务器的部署坑
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

洛谷P5661:公交换乘 ← CSP-J 2019 复赛第2题
【题目来源】https://www.luogu.com.cn/problem/P5661https://www.acwing.com/problem/content/1164/【题目描述】 著名旅游城市 B 市为了鼓励大家采用公共交通方式出行,推出了一种地铁换乘公交车的优惠方案: 1.在搭乘一次地铁后可以获得一张优惠票&…...

mysql优化之索引
索引官方定义:索引是帮助mysql高效获取数据的数据结构。 索引的目的在于提高查询效率,可以类比字典。 可以简单理解为:排好序的快速查找数据结构 在数据之外,数据库系统还维护着满足特定查找算法的数据结构,这种数据…...
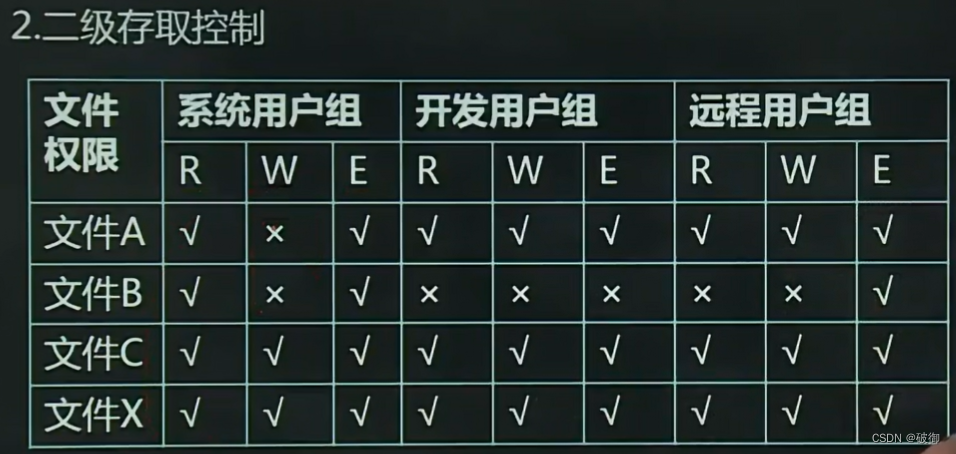
文件系统详解
目录 文件系统(1) 第一节文件系统的基本概念 一、文件系统的任务 二、文件的存储介质及存储方式 三、文件的分类 第二节 文件的逻辑结构和物理结构 一、文件的逻辑结构 二、文件的物理结构 文件系统(2) 第三节 文件目…...

有名管道及其应用
创建FIFO文件 1.通过命令: mkfifo 文件名 2.通过函数: mkfifo #include <sys/types.h> #include <sys/stat.h> int mkfifo(const char *pathname, mode_t mode); 参数: -pathname:管道名称的路径 -mode:文件的权限&a…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
