[题] n-皇后问题 #深搜 #DFS
题目 AcWing 843. n-皇后问题
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 20;
int n, p[N];
char g[N][N];
bool col[N], dg[N], udg[N];
void D (int u){if(u == n){for(int j = 0; j < n; j ++ )puts(g[j]);cout << endl;return ;}for(int i = 0; i < n; i ++)if( !col[i] && !dg[u + i] && !udg[n - u + i] ){g[u][i] = 'Q';col[i] = dg[u + i] = udg[n - u + i] = 1;p[u] = i;D(u + 1);g[u][i] = '.';col[i] = dg[u + i] = udg[n - u + i] = 0;}return ;
}
int main(){cin >> n;for(int i = 0; i < n; i ++)for(int j = 0; j < n; j ++)g[i][j] = '.';D(0);return 0;
}
/*
*0 搜索方式 : 深搜。具体操作:先遍历 第0行 可以放皇后的所有位置,再遍历 第1行 可以放皇后的位置...依次类推到 第n行。*1 补英文:column 列diagonal 对角线row 行
*2 这里 u+i 以及 n-u+i 分别是 (u,i)所在的对角线(这样的 /) 以及 反对角线(这样的 \)具体推导是: 令 (u, i) 为 在坐标轴上的 (x, y);(x, y)分别在对角线 y = x + b 以及 反对角线 y = -x + b 上。坐标轴上的 y=x+b => b=x-y => b=n+x-y (防止出现负数) ;以及 y=-x+b => b=x+y 。这时的 b 就是 (u,i) 所在的 对角线(或反对角线)的唯一编号;这样下来,在同一对角线的所有点就有了一样的唯一编号。(具体多少不重要u, i 可调换)
*3 p[u] 表示第u 行放的皇后的位置。
*4 时间是 18ms 左右;
*//**2点中说的对角线上的 u, i 调换对比版,答案是一样的。不用纠结 对角线和反对角线 这里的坐标序号之类的。
#include<bits/stdc++.h>
using namespace std;
const int N = 20;
int n, p[N];
char g[N][N];
bool col[N], dg[N], udg[N];
void D (int u){if(u == n){for(int j = 0; j < n; j ++ )puts(g[j]);cout << endl;return ;}for(int i = 0; i < n; i ++)if( !col[i] && !dg[i + u] && !udg[n - i + u] ){g[u][i] = 'Q';col[i] = dg[i + u] = udg[n - i + u] = 1;p[u] = i;D(u + 1);g[u][i] = '.';col[i] = dg[i + u] = udg[n - i + u] = 0;}return ;
}
int main(){cin >> n;for(int i = 0; i < n; i ++)for(int j = 0; j < n; j ++)g[i][j] = '.';D(0);return 0;
}*/
/*
原始的 “选与不选”搜索方法;
从(0,0) 一直依次遍历到 (n,n),对于每一个格子的操作是(放皇后或不放皇后);
时间是 107ms左右 ,不如上一个算法;
#include<bits/stdc++.h>
using namespace std;
const int N = 20;
int n ;
char g[N][N];
bool col[N], dg[N], udg[N], row[N];
void D (int x, int y, int s){if(y == n){x ++;y = 0;}if(x == n){if(s == n){for(int i = 0; i < n; i ++)puts(g[i]);cout << endl;}return ;}D(x, y + 1, s);if(!row[x] && !col[y] && !dg[n - x + y] && !udg[x + y]){row[x] = col[y] = dg[n - x + y] = udg[x + y] = 1;g[x][y] = 'Q';D(x, y + 1, s + 1);g[x][y] = '.';row[x] = col[y] = dg[n - x + y] = udg[x + y] = 0;}
}
int main(){cin >> n;for(int i = 0; i < n; i ++)for(int j = 0; j < n; j ++)g[i][j] = '.';D(0, 0, 0);return 0;
}
*/相关文章:

[题] n-皇后问题 #深搜 #DFS
题目 AcWing 843. n-皇后问题 代码 #include<bits/stdc.h> using namespace std; const int N 20; int n, p[N]; char g[N][N]; bool col[N], dg[N], udg[N]; void D (int u){if(u n){for(int j 0; j < n; j )puts(g[j]);cout << endl;return ;}for(int i…...

十小时开源了一个加密算法仓库,功能强大,后端开发人员狂喜!
写在前面 昨晚上睡觉前我就在想能不能把多个加密算法集成到一个库中,方便开发者调用,说干就干,今天肝了一天,中午直接吃的外卖哈哈哈哈,终于把仓库开源了,欢迎各位Go开发者Star和Fork! 仓库地址 go-cryp…...

标准化套利的使用
交易对象:目前使用郑商所,大商所的spd标准化套利组合进行交易。 交易平台:易盛极星极星产品网 手续费研究:白糖期货手续费和保证金2023年09月更新 - 九期网 本人使用的期货交易公司:中信期货(幸亏资金量大ÿ…...
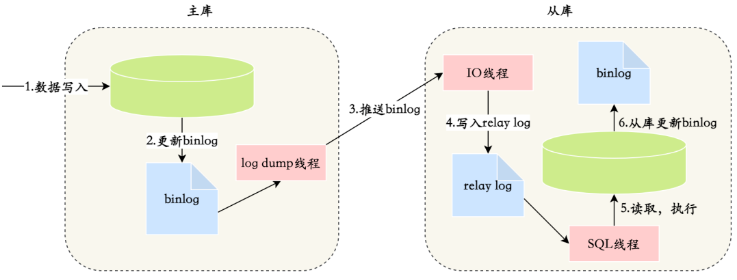
【MySQL数据库事务操作、主从复制及Redis数据库读写分离、主从同步的实现机制】
文章目录 MySQL数据库事务操作、主从复制及Redis数据库读写分离、主从同步的实现机制ACID及如何实现事务隔离级别:MVCC 多版本并发控制MySQL数据库主从复制主从同步延迟怎么处理Redis 读写分离1.什么是主从复制2.读写分离的优点 Redis为什么快呢? MySQL数…...
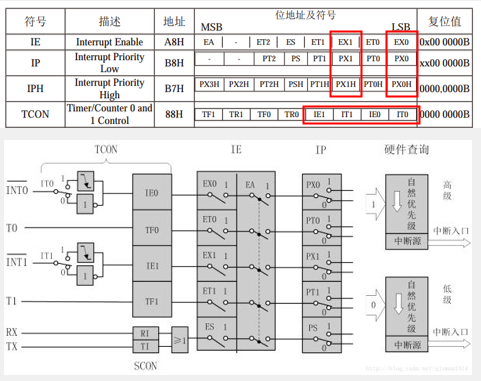
十五、红外遥控器
十五、红外遥控器 介绍基本接收和发送遥控器键码外部中断和外部中断寄存器 红外解码中断函数红外遥控电机模块电机调速 介绍 基本接收和发送 空闲状态:红外LED不亮,接收头输出高电平发送低电平:红外LED以38KHz闪烁,接收头输出低…...

diot函数解析
文章目录 前言一、Rio_readinitb二、Rio_readlineb三、strstr四、strcat五、Open_clientfd六、Rio_writen总结 前言 备战CSAPP中的ProxyLab时解析书上的diot函数中遇到了一些不会的函数,遂解析记录。 一、Rio_readinitb 读和解析请求行 Rio_readinitb(&rio,…...

Python函数绘图与高等代数互融实例(一):正弦函数与余弦函数
Python函数绘图与高等代数互融实例(一):正弦函数与余弦函数 Python函数绘图与高等代数互融实例(二):闪点函数 Python函数绘图与高等代数互融实例(三):设置X|Y轴|网格线 Python函数绘图与高等代数互融实例(四):设置X|Y轴参考线|参考区域 Python函数绘图与高等代数互融实例(五…...
Python 判断回文数
"""判断输入的数是否为回文数介绍:回文数:数字从高位到低位正序排列和低位到高位逆序排列都是同一数值例如:数字 1221 无论正序还是逆序都是 1221知识点:1、获取字符串长度函数len()2、条件语句if/elif/else3、循环…...

人工智能在金融领域的五个应用案例
随着科技的进步,人工智能(Artificial Intelligence,AI)正逐渐渗透到各个行业中,其中包括金融领域。本文介绍人工智能在金融领域的五个应用案例,以期帮助大家更好地了解这个新兴技术在金融中的价值和作用。 文章目录 Part1 风险管理…...

java 工程管理系统源码+项目说明+功能描述+前后端分离 + 二次开发
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目显示…...
:构造/析构/赋值运算)
Effective C++看书笔记(2):构造/析构/赋值运算
构造/析构/赋值运算 5:了解C默默编写并调用哪些函数6:如果不想使用编译器自动生成的函数,就该明确拒绝7:为多态基类声明virtual析构函数8:别让异常逃离析构函数9:绝不在构造和析构过程中调用virtual函数10&…...

交换奇偶位:交换一个整数的二进制的奇偶位置(仅考虑正数情况)
方法二: 设计思想: 0xAAAAAAAA 的二进制表示为 10101010...(从最低位开始) 0x55555555 的二进制表示为 01010101...(从最低位开始) 问题:更加想不到掩码!!…...

Unity中的两种ScriptingBackend
一:前言 二:两种模式的介绍 ios:unity只有il2cpp模式的编译才支持64位系统,mono是不支持的,在快速开发阶段仍然支持Mono,但是不能再向Apple提交Mono(32位)的应用 苹果在2016年1月就要求所有新上架游戏必须支…...
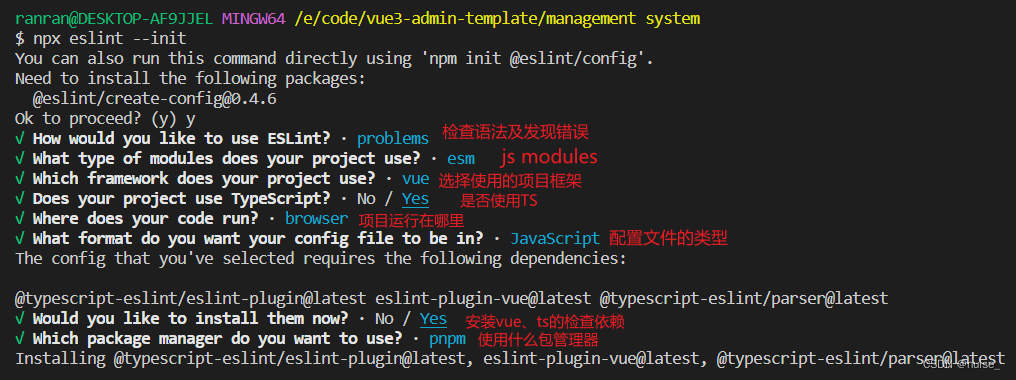
vue3硅谷甄选01 | 使用vite创建vue3项目及项目的配置 环境准备 ESLint配置 prettier配置 husky配置 项目集成
文章目录 使用vite创建vue3项目及项目的配置1.环境准备2.项目配置ESLint校验代码工具配置 - js代码检测工具1.安装ESLint到开发环境 devDependencies2.生成配置文件:.eslint.cjs**3.安装vue3环境代码校验插件**4. 修改.eslintrc.cjs配置文件5.生成ESLint忽略文件6.在package.js…...
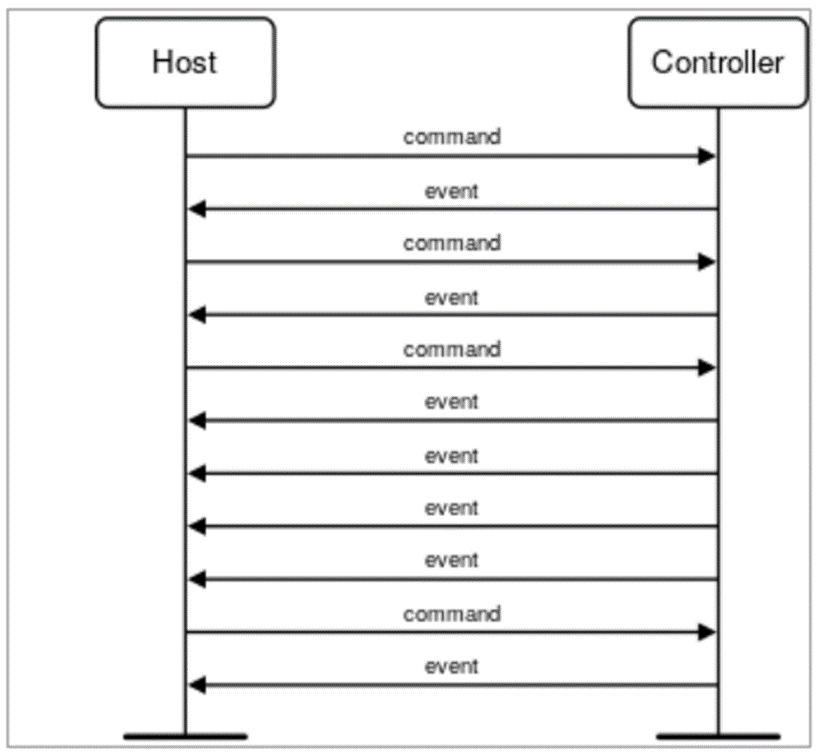
蓝牙核心规范(V5.4)10.5-BLE 入门笔记之HCI
HCI全称:HOST Constroller Interface 主机控制器接口(HCI)定义了一个标准化的接口,通过该接口,主机可以向控制器发出命令,并且控制器可以与主机进行通信。规范被分成几个部分,第一部分仅从功能的角度定义接口,不考虑具体的实现机制,而其他部分定义了在使用四种可能的…...
【计算机毕业设计】基于SpringBoot+Vue记帐理财系统的设计与实现
博主主页:一季春秋博主简介:专注Java技术领域和毕业设计项目实战、Java、微信小程序、安卓等技术开发,远程调试部署、代码讲解、文档指导、ppt制作等技术指导。主要内容:毕业设计(Java项目、小程序、安卓等)、简历模板、学习资料、…...

2023年中国研究生数学建模竞赛E题
出血性脑卒中临床智能诊疗建模 一、背景介绍 出血性脑卒中指非外伤性脑实质内血管破裂引起的脑出血,占全部脑卒中发病率的10-15%。其病因复杂,通常因脑动脉瘤破裂、脑动脉异常等因素,导致血液从破裂的血管涌入脑组织,从而造成脑部…...
基于springboot+vue的大学生科创项目在线管理系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

什么是文档签名证书?PDF文档怎么签名?
什么是文档签名证书?在“互联网”时代,电子合同、电子证照、电子病历、电子保单等各类电子文档无纸化应用成为常态。如何让电子文档的签署、审批具有公信力及法律效力,防止伪造签名、假冒签名等问题出现,是电子文档无纸化应用的主…...

2023年汉字小达人区级比赛倒计时2天,最新问题解答和真题练一练
今天是9月23日,距离2023年第十届汉字小达人区级比赛(初赛)的自由报名参赛时间还有2天,六分成长结合家长和小朋友们问的比较多的问题进行解答,并提供一些真题供大家练习、了解比赛题型和规则。 问题1:2023年…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...
