奇舞周刊第507期:通过 View Transition API 在状态之间添加丰富的过渡动画
记得点击文章末尾的“ 阅读原文 ”查看哟~
下面先一起看下本期周刊 摘要 吧~
奇舞推荐
■ ■ ■
通过 View Transition API 在状态之间添加丰富的过渡动画
W3C 2023 年度全球技术大会 (TPAC2023) 于今年9月 11 - 15 日召开。W3C CSS 工作组成员 Bramus Van Damme(Google) 为本届大会制作视频介绍 CSS 视图过渡模块:View Transition API 允许 DOM 更改在状态之间流畅地进行动画。这是通过利用用户代理 (UA) 的能力来保持状态的可视表示 (即快照) 并将它们与当前 DOM 状态的可视输出混合来实现的。该 API 还允许通过标准的 CSS 动画属性自定义动画。该规范描述了 single-page transition API 的 CSS 和 JS 机制。
基于 RPC 和 TypeScript 的 BFF 设计与实践
介绍了基于 RPC 和 TypeScript 的 BFF(Backend for frontend) 设计与实践。首先介绍了为什么需要 BFF,随着微服务和多终端发展趋势,传统的接口设计已经无法满足需求。然后,比较了 BFF 的几种实现方式,包括朴素模式和解耦模式,并分析了它们的优缺点。接着,介绍了 RPC-BFF 的技术选型,包括 gRPC、tRPC 和 DeepKit,并指出它们的局限性。最后详细介绍了自研 RPC-BFF 的设计与实现,包括 RPC-BFF 的 Schema 设计和 RPC 函数的定义。通过 RPC-BFF,可以实现类型安全、高效的前后端数据交互。
JavaScript 打包下载最佳实践:StreamSaver.js + zip-stream.js 流式下载
介绍了使用 StreamSaver.js 和 zip-stream.js 实现 JavaScript 打包下载的最佳实践。通常在用户需要下载多个文件时,可以采用浏览器打包下载的方式,减少服务器流量和性能消耗。详细介绍了使用 StreamSaver.js 和 zip-stream.js 的步骤和方法,并提供了同步和异步两种打包下载的函数。最后,给出了调用函数进行下载的示
技术实践
■ ■ ■
React 最佳实践之“你可能不需要 Effect”
本文思想来自 React 官方文档 You Might Not Need an Effect,保熟,是我近几天读了 n 遍之后自己的理解,感觉受益匪浅,这里小记一下跟大家分享。曾经本小白 R 的水平一直停留在会用 React 写业务,讲究能跑就行的程度,最近尝试学习一些关于 React 的最佳实践,感兴趣的朋友一起上车吧!!
探究 canvas 环形进度条及其背后的原理
在银行做前端开发,最痛苦的莫过于内网开发,很多第三方库和组件无法使用,只能自己造轮子,真可谓是举步维艰!上周写过一篇《纯 css 轻松实现环形进度条》,就像标题所说,实现起来确实“轻松”,不过也因此受到一些限制,例如无法让进度条两头呈现圆形,也无法做出动画加载进度的效果。
如何写一个属于自己的 Vue3 组件库
目前流行的组件库搭建方式都是使用 monorepo 的方式,好处很多,可以在一个代码仓库中管理多个项目,可以达到项目之间的资源共享。这里也是使用这种方式。
拓展边界
■ ■ ■
Chrome 117 更新:Network 面板就能发起 Mock 请求!!!
前端开发在调试过程中,经常需要各种不同的数据来反复调试,所以我们前端程序员会经常在脚手架中集成 mock 或者通过代理的方式去 hack 的实现,但是现在再也不用这么麻烦了,Chrome 117 原生就支持了,而且体验相当丝滑。
【动画进阶】当路径动画遇到滚动驱动!
在一年前,我介绍了 CSS 中非常新奇有趣的一个新特性 -- @scroll-timeline:革命性创新,动画杀手锏 @scroll-timeline[1]。利用这个新特性,我们可以轻松的将原本基于时间控制的动画效果,交给页面的滚动特性进行控制,像是这样:只是,该特性由于诸多原因,遭到了规范废弃。然而,时隔一年半,规范带着新的 animation-timeline[2] 王者回归!我们可以将其简单理解为:Scroll-driven Animations (滚动驱动动画)。
关于奇舞团
奇舞团是 360 集团最大的大前端团队,代表集团参与 W3C 和 ECMA 会员(TC39)工作。奇舞团非常重视人才培养,有工程师、讲师、翻译官、业务接口人、团队 Leader 等多种发展方向供员工选择,并辅以提供相应的技术力、专业力、通用力、领导力等培训课程。奇舞团以开放和求贤的心态欢迎各种优秀人才关注和加入奇舞团。

相关文章:

奇舞周刊第507期:通过 View Transition API 在状态之间添加丰富的过渡动画
记得点击文章末尾的“ 阅读原文 ”查看哟~ 下面先一起看下本期周刊 摘要 吧~ 奇舞推荐 ■ ■ ■ 通过 View Transition API 在状态之间添加丰富的过渡动画 W3C 2023 年度全球技术大会 (TPAC2023) 于今年9月 11 - 15 日召开。W3C CSS 工作组成员 Bramus Van Damme(Google) 为本届…...

如何通过技术变现
技术变现是指将技术转化为实际价值的过程。以下是几种常见的技术变现方式: 软件开发与销售:根据市场需求开发软件,并将其销售给需要的企业或个人。专利许可与授权:将技术成果申请专利,通过专利许可和授权给企业使用&a…...
高效查询大量快递信息,轻松掌握技巧
在如今快节奏的生活中,快递已经成为我们日常不可或缺的一部分。然而,对于一些忙碌的人来说,单个查询每一个快递单号可能会浪费太多时间。因此,我们需要一款可以帮助我们批量查询快递的软件。 在市场上,有很多款专门用于…...

iperf3: error - unable to connect to server: No route to host 但嵌入式Linux设备
起因 需要测试WIFI设置为802.11n制式能否输出40MHZ带宽去做CE认证 需要一台设备WIFI 设置为STA模式 一台设备WIFI设置为AP模式 用STA模式的设备去连接AP模式的设备才能产生40MH带宽 起初用了一台设备做STA模式设备(设备A)来测试没问题了,要换一台设备做STA设备(设备…...

OpenCV自学笔记十七:傅里叶变换
1、Numpy实现傅里叶变换 傅里叶变换(Fourier Transform)是一种将信号从时域转换到频域的数学变换。它将一个连续或离散的时域信号分解为一组正弦和余弦函数的复合。 在Python中,可以使用NumPy库来实现傅里叶变换。具体步骤如下:…...

uniapp如何判断是哪个(微信/APP)平台
其实大家在开发uniapp项目的时候长长会遇到这样一个问题,就是针对某些小程序,没发去适配相关的功能,所以要针对不同的平台,进行不同的处理。 #ifdef : if defined 仅在某个平台编译 #ifndef : …...
网络安全——(黑客)自学
想自学网络安全(黑客技术)首先你得了解什么是网络安全!什么是黑客!!! 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队…...

一拖三快充线(USB-C转三充)的解决方案--LDR6020P
DR6020P 是带有 3 组 6 路 DRP USB-C 及 PD 通信协议处理模块和 USB2.0 Device 功能的 16 位 RISC MCU,内置 8K16 位 MTP 程序存储器(可烧录 1000 次),512 字节的数据存储器(SRAM)。内置 LDO 5V 输出&#…...
2024年考研教育专业的教育综合考试大纲、样题和往年真题
根据教育部通知,2024年全国硕士研究生招生考试初试定于2023年12月23日至24日,即我们说的2024年考研时间为12月23-24日。距离现在只剩下3个月不到的时间,那么如何让我们在最后三个月内的复习和备考有效且高效呢? 结合很多清北复交研…...
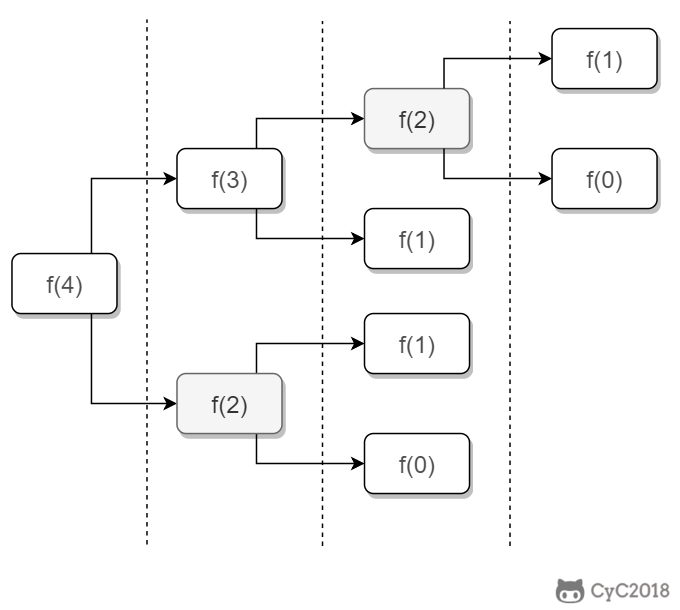
算法之斐波那契数列
10.1 斐波那契数列 题目链接 牛客网 题目描述 求斐波那契数列的第 n 项,n < 39。 解题思路 如果使用递归求解,会重复计算一些子问题。例如,计算 f(4) 需要计算 f(3) 和 f(2),计算 f(3) 需要计算 f(2) 和 f(1),…...
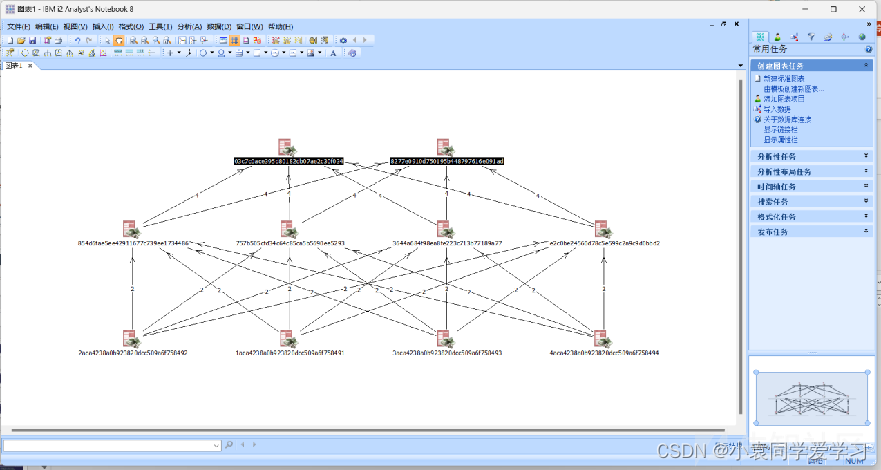
关于Pandas数据分析
pandas的数据加载与预处理 数据清洗:洗掉脏数据 整理分析:字不如表 数据展现:表不如图 环境搭建 pythonjupyter anaconda Jupyter Notebook Jupyter Notebook可以在网页页面中直接编写代码和运行代码, 代码的运行结果也会直接在代码块下显示…...
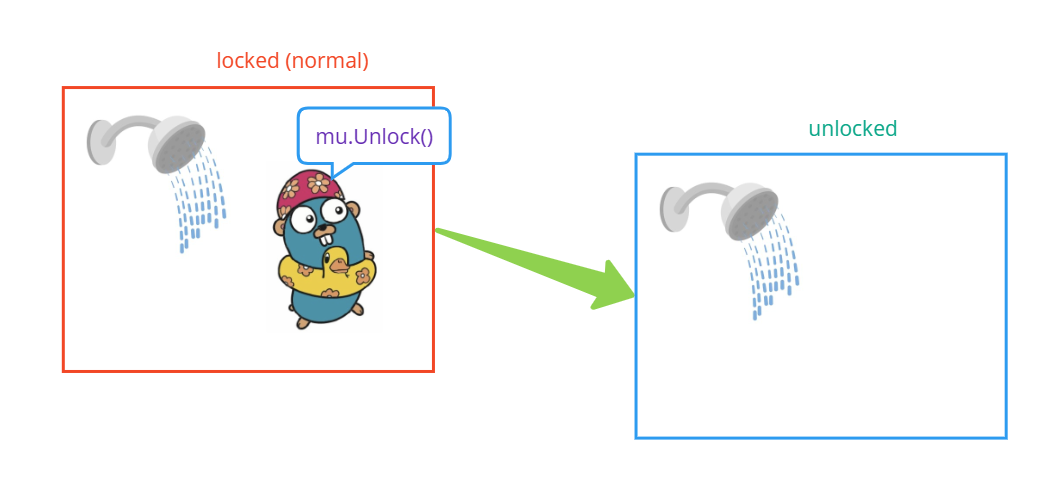
Go 并发可视化解释 - sync.Mute
在学习 Go 编程语言时,您可能会遇到这句著名的格言:“不要通过共享内存来进行通信;相反,通过通信来共享内存。” 这句话构成了 Go 强大并发模型的基础,其中通道(channels)作为协程之间的主要通信…...
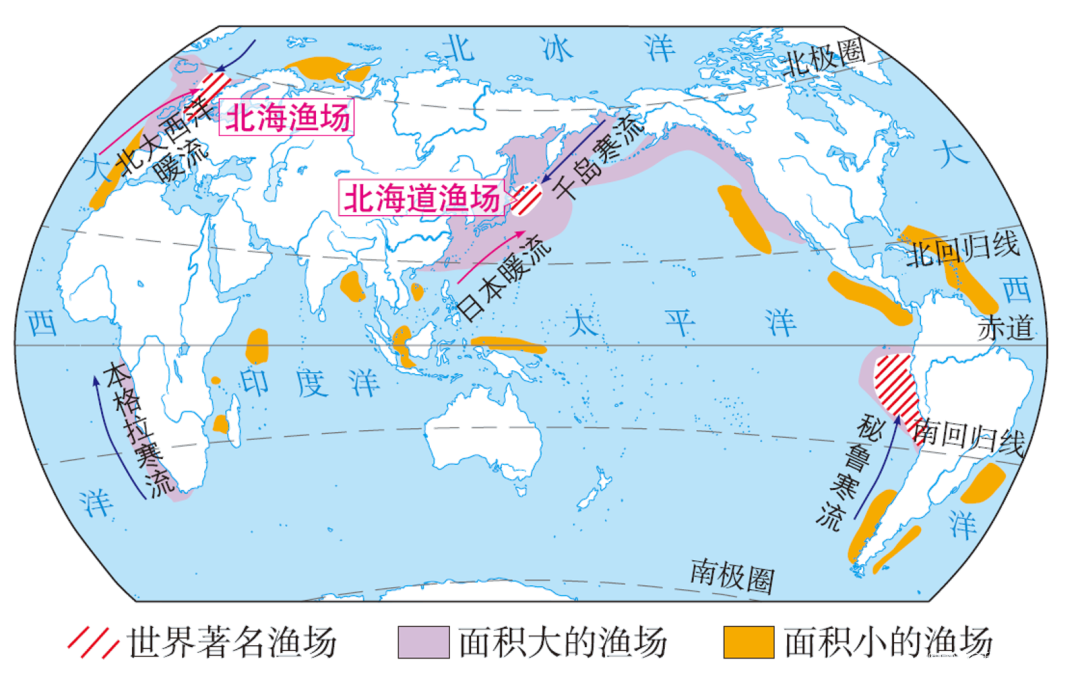
十几张高清世界地图
十几张高清世界地图 仅供学习!...
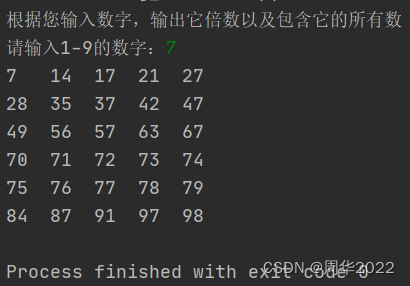
Python 逢七拍手游戏
"""逢七拍手游戏介绍:逢七拍手游戏的规则是:从1开始顺序数数,数到有7,或者是7的倍数时,就拍一手。例如:7、14、17......70......知识点:1、循环语句for2、嵌套条件语句if/elif/e…...
Windows安装Mysql--免安装版
在Windows系统上安装免安装版MySql的步骤 官方下载地址:https://dev.mysql.com/downloads/mysql/ 将下载好的文件“mysql-5.7.18-winx64”解压缩到C盘的 目录下: 配置环境变量: (略) 正式安装,添加my.i…...

TypeScript中常见的操作符运算符总结
一、非空断言操作符(!) 当我们⽆法断定类型时,可以使用后缀表达式操作符 ! 来断⾔操作对象是⾮ null 或⾮ undefined 类型。 具体来说,比如表达式: x ! , 结果将从 x 值域中排除 null 和 unde…...

什么是泛型约束?
泛型约束(Generic Constraints)是一种在使用泛型时限制可接受类型的方式。它允许我们对泛型类型参数进行限定,以确保只有符合特定条件的类型才能被使用。 泛型约束的作用是提供更精确的类型控制和更强的类型安全性。通过约束泛型类型参数&am…...

代码随想录算法训练营 动态规划part11
一、买卖股票的最佳时机III 123. 买卖股票的最佳时机 III - 力扣(LeetCode) 请选一个喜欢的吧/(ㄒoㄒ)/~~123. 买卖股票的最佳时机 III - 力扣(LeetCode) class Solution {public int maxProfit(int[] prices) {if(pricesnul…...
复习——Lesson 16 - Lesson20)
新概念英语(第二册)复习——Lesson 16 - Lesson20
前言 新概念英语的16-20课,从21课开始,每天一课的速度更新,方便你能快速跟上。 文章目录 前言Lesson 16 - A polite request原文译文单词 Lesson 17 - Always Young原文译文单词 Lesson 18 - He often does this!原文译文单词Lesson 19 - So…...

[题] n-皇后问题 #深搜 #DFS
题目 AcWing 843. n-皇后问题 代码 #include<bits/stdc.h> using namespace std; const int N 20; int n, p[N]; char g[N][N]; bool col[N], dg[N], udg[N]; void D (int u){if(u n){for(int j 0; j < n; j )puts(g[j]);cout << endl;return ;}for(int i…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...
