怒刷LeetCode的第10天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:两次拓扑排序
第二题
题目来源
题目内容
解决方法
方法一:分治法
方法二:优先队列(Priority Queue)
方法三:迭代
第三题
题目来源
题目内容
解决方法
方法一:迭代
方法二:递归
方法三:双指针
方法四:栈
第一题
题目来源
2603. 收集树中金币 - 力扣(LeetCode)
题目内容
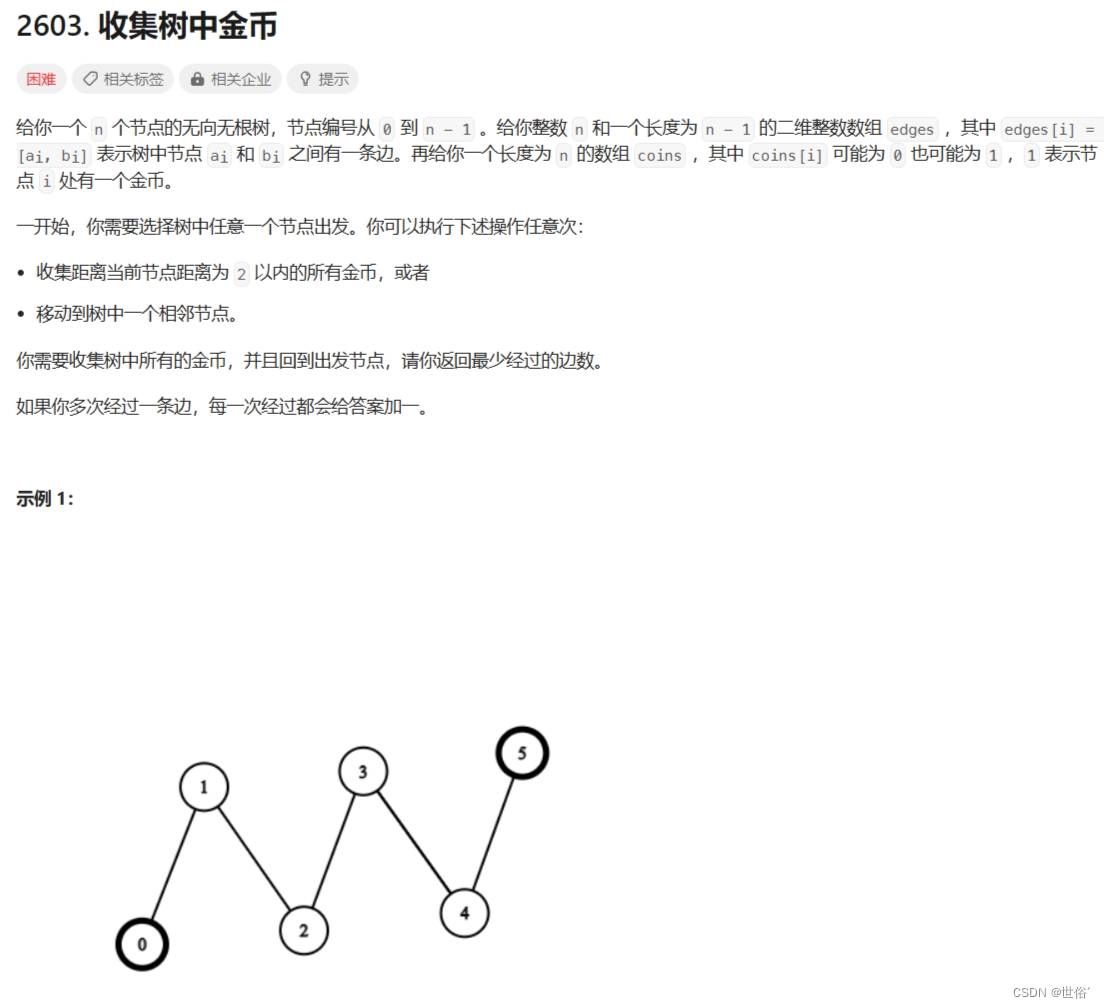
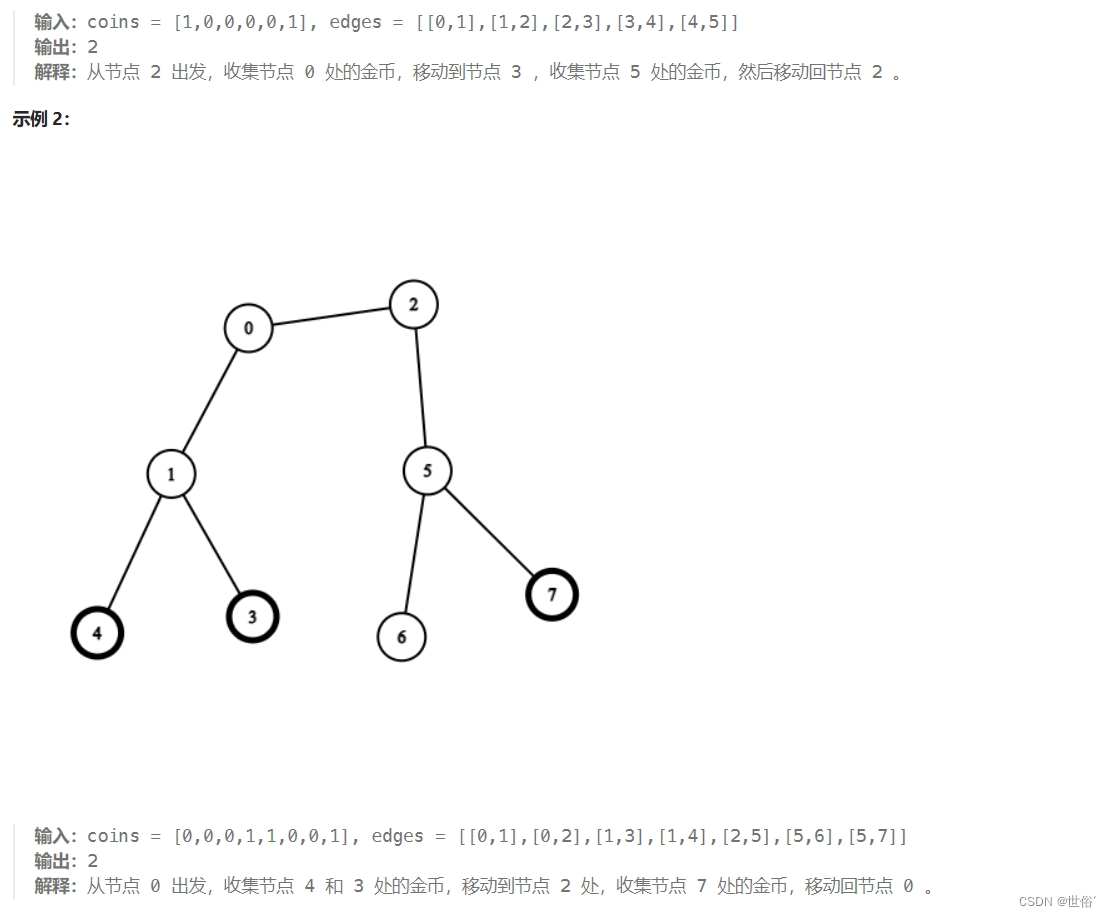

解决方法
方法一:两次拓扑排序
这个解法的思路如下:
- 首先,初始化一个邻接表 g,用于存储树的结构,以及一个数组 degree,用于记录每个节点的度数。
- 遍历边的数组 edges,将每条边的两个节点之间建立连接关系,并更新节点的度数。
- 初始化一个队列 queue,用于存储无金币的叶子节点。
- 遍历所有节点,如果一个节点的度数为1并且该节点没有金币,则将其加入队列。
- 开始循环,直到队列为空。在每次迭代中,取出队列的首个节点 u。
- 将节点 u 的度数减1,剩余节点数 rest 减1。
- 遍历与节点 u 相邻的所有节点 v,将其度数减1。
- 如果节点 v 的度数为1并且该节点没有金币,则将其加入队列。
- 重复步骤 5-8,直到队列为空。
- 重复两次以下步骤(总共遍历两次): a. 初始化一个新的队列 queue。 b. 遍历所有节点,将度数为1的节点加入队列。 c. 开始循环,直到队列为空。 d. 取出队列的首个节点 u,将其度数减1,剩余节点数 rest 减1。 e. 遍历与节点 u 相邻的所有节点 v,将其度数减1。 f. 重复步骤 d-e,直到队列为空。
- 返回结果,如果剩余节点数 rest 为0,则路径长度为0;否则,路径长度为 (rest - 1) * 2。
这样,通过删除树中无金币的叶子节点和维护节点的度数,可以得到最小路径长度。
class Solution {public int collectTheCoins(int[] coins, int[][] edges) {int n = coins.length;List<Integer>[] g = new List[n];for (int i = 0; i < n; ++i) {g[i] = new ArrayList<Integer>();}int[] degree = new int[n];for (int[] edge : edges) {int x = edge[0], y = edge[1];g[x].add(y);g[y].add(x);++degree[x];++degree[y];}int rest = n;/* 删除树中所有无金币的叶子节点,直到树中所有的叶子节点都是含有金币的 */Queue<Integer> queue = new ArrayDeque<Integer>();for (int i = 0; i < n; ++i) {if (degree[i] == 1 && coins[i] == 0) {queue.offer(i);}}while (!queue.isEmpty()) {int u = queue.poll();--degree[u];--rest;for (int v : g[u]) {--degree[v];if (degree[v] == 1 && coins[v] == 0) {queue.offer(v);}}}/* 删除树中所有的叶子节点, 连续删除2次 */for (int x = 0; x < 2; ++x) {queue = new ArrayDeque<Integer>();for (int i = 0; i < n; ++i) {if (degree[i] == 1) {queue.offer(i);}}while (!queue.isEmpty()) {int u = queue.poll();--degree[u];--rest;for (int v : g[u]) {--degree[v];}}}return rest == 0 ? 0 : (rest - 1) * 2;}
}复杂度分析:
1、构建邻接表和计算节点度数的复杂度:
- 遍历边的数组 edges,时间复杂度为 O(m),其中 m 是边的数量。
- 初始化邻接表 g 的空间复杂度为 O(n),其中 n 是节点的数量。
- 更新节点度数的过程需要遍历所有边,时间复杂度为 O(m)。
2、删除无金币叶子节点的过程的复杂度:
- 初始化队列的时间复杂度为 O(n),其中 n 是节点的数量。
- 每个节点最多被处理一次,因此删除过程的时间复杂度为 O(n)。
3、连续删除两次叶子节点的过程的复杂度:
- 需要进行两次完整的节点遍历,因此时间复杂度为 O(2n) = O(n),其中 n 是节点的数量。
综上所述,整个解法的时间复杂度为 O(m + n),其中 m 是边的数量,n 是节点的数量。空间复杂度为 O(n),用于存储邻接表和节点度数。
LeetCode运行结果:
第二题
题目来源
23. 合并 K 个升序链表 - 力扣(LeetCode)
题目内容

解决方法
方法一:分治法
这是一个合并K个升序链表的问题,可以使用分治法来解决。使用了分治法来将k个链表分成两部分进行合并,然后再将合并后的结果继续与剩下的链表合并,直到最终合并成一个升序链表。在每个合并的过程中,可以使用双指针来逐个比较两个链表的节点值,将较小的节点连接到结果链表上。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
public class Solution {public ListNode mergeKLists(ListNode[] lists) {if (lists == null || lists.length == 0) {return null;}return merge(lists, 0, lists.length - 1);}private ListNode merge(ListNode[] lists, int start, int end) {if (start == end) {return lists[start];}int mid = start + (end - start) / 2;ListNode left = merge(lists, start, mid);ListNode right = merge(lists, mid + 1, end);return mergeTwoLists(left, right);}private ListNode mergeTwoLists(ListNode l1, ListNode l2) {if (l1 == null) {return l2;}if (l2 == null) {return l1;}if (l1.val < l2.val) {l1.next = mergeTwoLists(l1.next, l2);return l1;} else {l2.next = mergeTwoLists(l1, l2.next);return l2;}}
}复杂度分析:
- 这个解法的时间复杂度是 O(Nlogk),其中 N 是所有链表的节点总数,k 是链表的数量。因为在每层合并的过程中,需要遍历 N 个节点来比较值,并且每次合并的链表数量减半,因此总共需要合并 logk 层。所以时间复杂度是 O(Nlogk)。
- 空间复杂度是 O(logk),主要是递归调用栈的空间。在每一层递归中,都会创建两个新的递归函数调用,所以递归的层数最多是 logk。因此,空间复杂度是 O(logk)。
需要注意的是,这里的空间复杂度是指除了返回的合并后的链表之外的额外空间使用量。
LeetCode运行结果:
方法二:优先队列(Priority Queue)
使用了优先队列来维护当前k个链表中的最小节点。首先,将所有链表的头节点加入到优先队列中。然后,不断从优先队列中取出最小的节点,将其加入到合并后的链表中,并将该节点的下一个节点加入到队列中。重复这个过程直到队列为空。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
public class Solution {public ListNode mergeKLists(ListNode[] lists) {if (lists == null || lists.length == 0) {return null;}// 创建一个优先队列,按照节点值的大小进行排序PriorityQueue<ListNode> queue = new PriorityQueue<>((a, b) -> a.val - b.val);// 将所有链表的头节点加入到优先队列中for (ListNode node : lists) {if (node != null) {queue.offer(node);}}// 创建一个dummy节点作为合并后的链表头部ListNode dummy = new ListNode(0);ListNode curr = dummy;// 不断从优先队列中取出最小的节点,将其加入到合并后的链表中,然后将该节点的下一个节点加入到队列中while (!queue.isEmpty()) {ListNode node = queue.poll();curr.next = node;curr = curr.next;if (node.next != null) {queue.offer(node.next);}}return dummy.next;}
}复杂度分析:
- 这个基于优先队列的解法的时间复杂度是O(Nlogk),其中N是所有链表的节点总数,k是链表的数量。主要的时间消耗在于构建优先队列和从队列中取出最小节点,而构建优先队列的时间复杂度是O(klogk),每次取出最小节点的操作时间复杂度是O(logk)。由于总共需要取出N个节点,因此总体的时间复杂度是O(Nlogk)。
- 空间复杂度是O(k),主要是优先队列所占用的空间。在最坏情况下,优先队列中最多会有k个节点,因此空间复杂度是O(k)。
需要注意的是,这里的空间复杂度是指除了返回的合并后的链表之外的额外空间使用量。
LeetCode运行结果:
方法三:迭代
使用了迭代的方式逐一合并链表。
- 首先设定一个变量 interval,初始值为1,表示每次合并的链表数量。
- 然后进行循环,直到 interval 大于等于链表数组的长度。在每次循环中,按照 interval 的步长对链表数组进行逐一合并。每次合并两个链表,将合并结果放回原始数组的相应位置。
- 通过每次将 interval 值翻倍,循环进行迭代合并,直到 interval 大于等于链表数组的长度,最终得到合并后的链表。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode mergeKLists(ListNode[] lists) {if (lists == null || lists.length == 0) {return null;}int interval = 1;while (interval < lists.length) {for (int i = 0; i + interval < lists.length; i += 2 * interval) {lists[i] = mergeTwoLists(lists[i], lists[i + interval]);}interval *= 2;}return lists[0];}private ListNode mergeTwoLists(ListNode l1, ListNode l2) {ListNode dummy = new ListNode(0);ListNode curr = dummy;while (l1 != null && l2 != null) {if (l1.val < l2.val) {curr.next = l1;l1 = l1.next;} else {curr.next = l2;l2 = l2.next;}curr = curr.next;}if (l1 != null) {curr.next = l1;}if (l2 != null) {curr.next = l2;}return dummy.next;}
}
复杂度分析:
- 时间复杂度:这个解法的时间复杂度是O(Nklogk),其中N是每个链表的平均长度,k是链表的数量。通过每次将 interval 值翻倍,循环进行迭代合并,直到 interval 大于等于链表数组的长度,最终得到合并后的链表。在每一层循环中的操作总时间复杂度仍然是O(Nk),因为每一层的合并操作需要遍历所有链表节点。
- 空间复杂度:这个解法的空间复杂度是O(1),没有使用额外的数据结构。只需要常数级别的额外空间来保存临时变量。
综上所述,优先队列解法和分治法解法的时间复杂度相同,但优先队列解法的空间复杂度略高于分治法解法。而迭代解法的时间复杂度稍高于前两种解法,并且空间复杂度较低。
LeetCode运行结果:
第三题
题目来源
24. 两两交换链表中的节点 - 力扣(LeetCode)
题目内容

解决方法
方法一:迭代
迭代的思路是遍历链表,每次处理两个相邻节点进行交换。具体步骤如下:
1、定义一个哑节点(dummy)作为新链表的头节点,并将其指向原始链表的头节点head。
2、定义一个指针prev指向哑节点,用于连接新链表中的节点。
3、当原始链表中至少有两个节点时,重复以下操作:
- 使用指针curr1指向当前要交换的第一个节点,即prev.next。
- 使用指针curr2指向当前要交换的第二个节点,即curr1.next。
- 将prev的下一个节点指向curr2,完成节点交换。
- 将curr1的下一个节点指向curr2的下一个节点,完成节点交换。
- 将curr2的下一个节点指向curr1,完成节点交换。
- 更新prev指针和curr1指针,使它们分别指向交换后的第二个节点和下一组要交换的第一个节点。
4、返回哑节点(dummy)的下一个节点作为新链表的头节点。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {
public ListNode swapPairs(ListNode head) {ListNode dummy = new ListNode(0);dummy.next = head;ListNode prev = dummy;while (head != null && head.next != null) {ListNode curr1 = head;ListNode curr2 = head.next;prev.next = curr2;curr1.next = curr2.next;curr2.next = curr1;prev = curr1;head = curr1.next;}return dummy.next;
}}复杂度分析:
- 时间复杂度:O(n),其中n是链表中的节点数。需要遍历链表中的每个节点一次。
- 空间复杂度:O(1)。只需要常数级别的额外空间。
LeetCode运行结果:
方法二:递归
递归的思路是将链表分成两部分:第一个节点和剩余节点。然后,交换这两部分,并递归地对剩余节点进行两两交换。具体步骤如下:
- 当链表为空或只有一个节点时,无需交换,直接返回该节点。
- 令first指向链表的头节点,second指向first的下一个节点。
- 交换first和second节点,即将second的next指向first,并将first的next指向递归处理剩余节点的结果。
- 返回second节点作为新链表的头节点。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {
public ListNode swapPairs(ListNode head) {if (head == null || head.next == null) {return head;}ListNode first = head;ListNode second = head.next;first.next = swapPairs(second.next);second.next = first;return second;
}
}复杂度分析:
- 时间复杂度:O(n),其中n是链表中的节点数。每次递归都会处理一个节点,并且递归调用的层数最多为n/2。
- 空间复杂度:O(n),其中n是链表中的节点数。递归调用的栈空间最多为n/2。
LeetCode运行结果:
方法三:双指针
除了递归和迭代之外,还可以使用双指针的方法来交换链表中的节点。该方法使用两个指针prev和curr分别指向当前要交换的两个节点的前一个节点和第一个节点。通过不断地交换节点,并更新指针,实现链表中节点的两两交换。
注意:它与迭代方法的思路类似,但在细节上有所改动。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {
public ListNode swapPairs(ListNode head) {// 创建哑节点(dummy)作为新链表的头节点,并将其指向原始链表的头节点headListNode dummy = new ListNode(0);dummy.next = head;// 定义两个指针prev和curr,分别指向当前要交换的两个节点的前一个节点和第一个节点ListNode prev = dummy;ListNode curr = head;while (curr != null && curr.next != null) {// 获取要交换的两个节点ListNode node1 = curr;ListNode node2 = curr.next;// 进行节点交换prev.next = node2;node1.next = node2.next;node2.next = node1;// 更新prev和curr指针,进行下一组节点交换prev = node1;curr = node1.next;}return dummy.next;
}}复杂度分析:
- 时间复杂度:O(n) 遍历链表中的每个节点一次,所以时间复杂度是线性的。
- 空间复杂度:O(1) 只使用了常数级别的额外空间,不随输入规模增加而变化。
LeetCode运行结果:

方法四:栈
除了递归、双指针和迭代之外,还可以使用栈来实现链表节点的两两交换。
这种栈的方法将链表中的节点依次入栈,每次栈中至少有两个节点时,就进行交换操作。通过维护栈来实现链表节点的两两交换。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {
public ListNode swapPairs(ListNode head) {// 创建一个栈Deque<ListNode> stack = new ArrayDeque<>();ListNode dummy = new ListNode(0);dummy.next = head;ListNode curr = dummy;while (curr != null && curr.next != null) {// 将当前节点的后继节点和后继的后继节点入栈stack.push(curr.next);stack.push(curr.next.next);// 当栈中至少有两个节点时,进行节点交换if (stack.size() >= 2) {curr.next = stack.pop();curr.next.next = stack.pop();curr = curr.next.next;} else {break;}}return dummy.next;
}}复杂度分析:
- 时间复杂度:O(n),其中 n 是链表的长度。需要遍历链表中的每个节点一次。
- 空间复杂度:O(n),需要使用一个栈来存储节点。
需要注意的是,递归的深度与链表的长度相关,当链表较长时可能会导致栈溢出,因此在实际使用时需要注意链表的长度限制。如果链表长度较大,建议使用其他方法实现节点的交换。
LeetCode运行结果:

相关文章:

怒刷LeetCode的第10天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:两次拓扑排序 第二题 题目来源 题目内容 解决方法 方法一:分治法 方法二:优先队列(Priority Queue) 方法三:迭代 第三题 题目来源 题目内容…...

java框架-Springboot3-场景整合
文章目录 java框架-Springboot3-场景整合批量安装中间件NoSQL整合步骤RedisTemplate定制化 接口文档远程调用WebClientHttp Interface 消息服务 java框架-Springboot3-场景整合 批量安装中间件 linux安装中间件视频 NoSQL 整合redis视频 整合步骤 RedisTemplate定制化 Re…...
在Bat To Exe Converter,修改为当异常结束或终止时,程序重新启动执行
在Bat To Exe Converter,修改为当异常结束或终止时,程序重新启动执行 .bat中的代码部分: .bat中的代码echo offpython E:\python\yoloProjectTestSmallLarge\detect.pypause,我想你能帮在Bat To Exe Converter,修改成…...
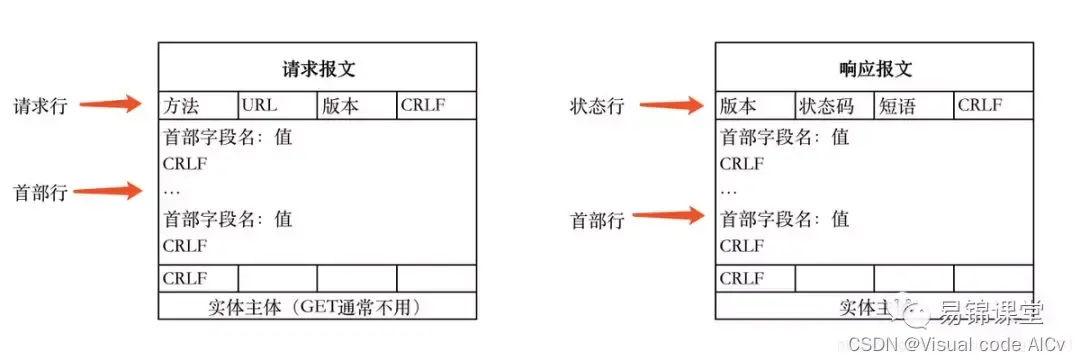
PythonWeb服务器(HTTP协议)
一、HTTP协议与实现原理 HTTP(Hypertext Transfer Protocol,超文本传输协议)是一种用于在网络上传输超文本数据的协议。它是Web应用程序通信的基础,通过客户端和服务器之间的请求和响应来传输数据。在HTTP协议中连接客户与服务器的…...
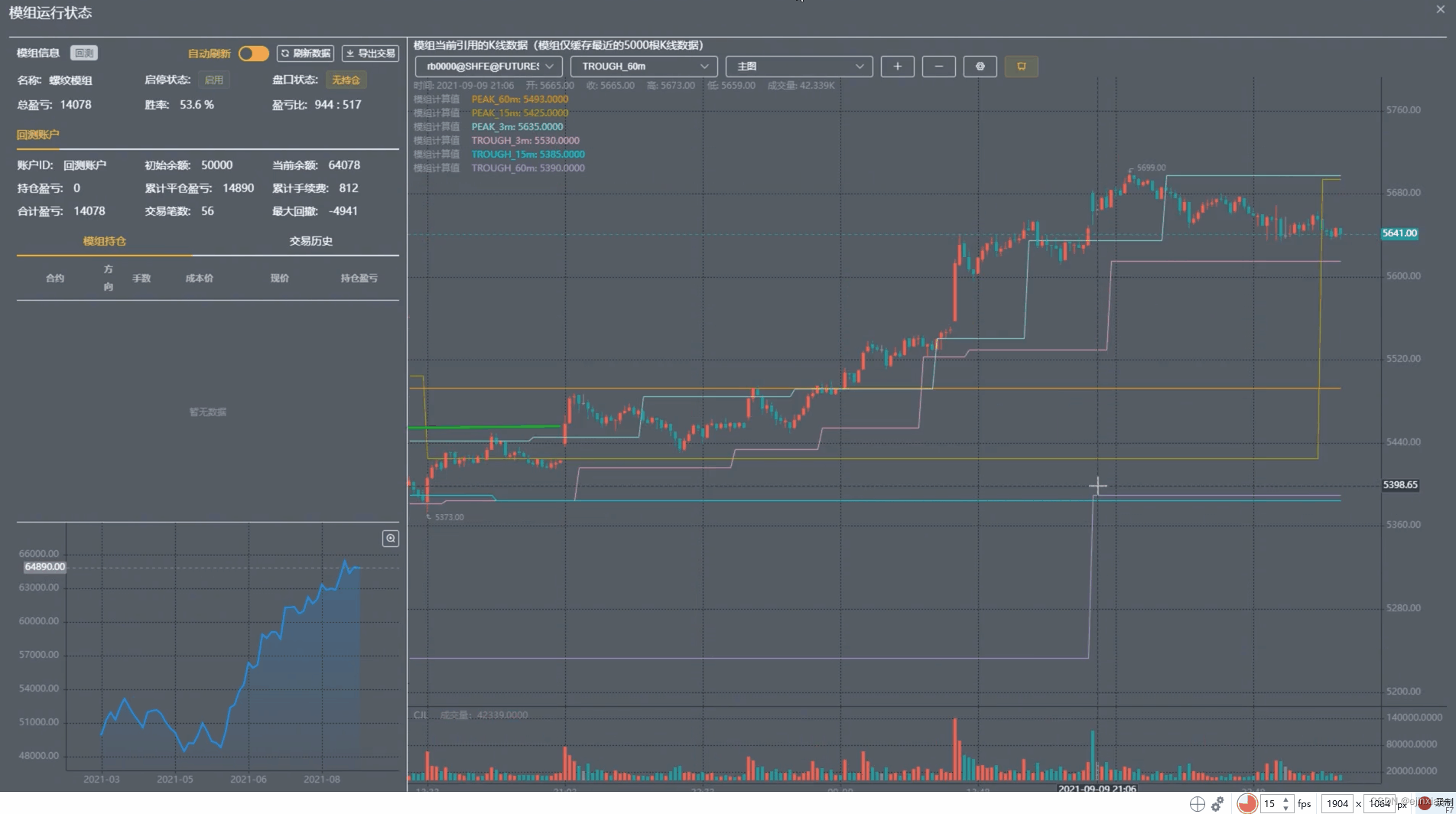
Northstar 量化平台
基于 B/S 架构、可替代付费商业软件的一站式量化交易平台。具备历史回放、策略研发、模拟交易、实盘交易等功能。兼顾全自动与半自动的使用场景。 已对接国内期货股票、外盘美股港股。 面向程序员的量化交易软件,用于期货、股票、外汇、炒币等多种交易场景ÿ…...

c语言进阶部分详解(经典回调函数qsort()详解及模拟实现)
大家好!上篇文章(c语言进阶部分详解(指针进阶2)_总之就是非常唔姆的博客-CSDN博客)我已经对回调函数进行了初步的讲解和一个简单的使用事例,鉴于篇幅有限没有进行更加详细的解释,今天便来补上。…...

win下 lvgl模拟器codeblocks配置
链接: 官方lvgl的codeblocks官方例子 下载慢的话,可能需要点工具。 需要下载的东西 https://github.com/lvgl/lv_port_win_codeblocks https://github.com/lvgl/lv_drivers/tree/4f98fddd2522b2bd661aeec3ba0caede0e56f96b https://github.com/lvgl/lvgl/tree/7a23…...
Quartus出租车计价器VHDL计费器
名称:出租车计价器VHDL计费器 软件:Quartus 语言:VHDL 要求: 启动键start表示汽车启动,起步价7元,同时路程开始计数,停止键stop表示熄火,车费和路程均为0,当暂停键pa…...
浅谈单元测试:测试和自动化中的利用
【软件测试面试突击班】如何逼自己一周刷完软件测试八股文教程,刷完面试就稳了,你也可以当高薪软件测试工程师(自动化测试) 浅谈单元测试是一件棘手的事情。我很确定测试人员在某个时候会抱怨开发人员没有正确地进行单元测试&…...

深度详解Java序列化
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
)
Linux下的网络编程——B/S模型HTTP(四)
前言: HTTP是基于B/S架构进行通信的,而HTTP的服务器端实现程序有httpd、nginx等,其客户端的实现程序主要是Web浏览器,例如Firefox、Internet Explorer、Google Chrome、Safari、Opera等,此外,客户端的命令…...

Go语言入门篇
目录 一、基础数据类型 1.1 变量的定义方式 1.2 用%T输出变量的类型 二、复合数据类型 2.1 数组 2.1.2、数组的遍历 2.1.3 数组传参 2.2. 切片slice 2.2.1. 初始化切片 2.2.2. append向切片中追加元素 2.2.3. 切片的截取 2.3. map 2.3.1. map初始化 2.3.2. 添加和…...
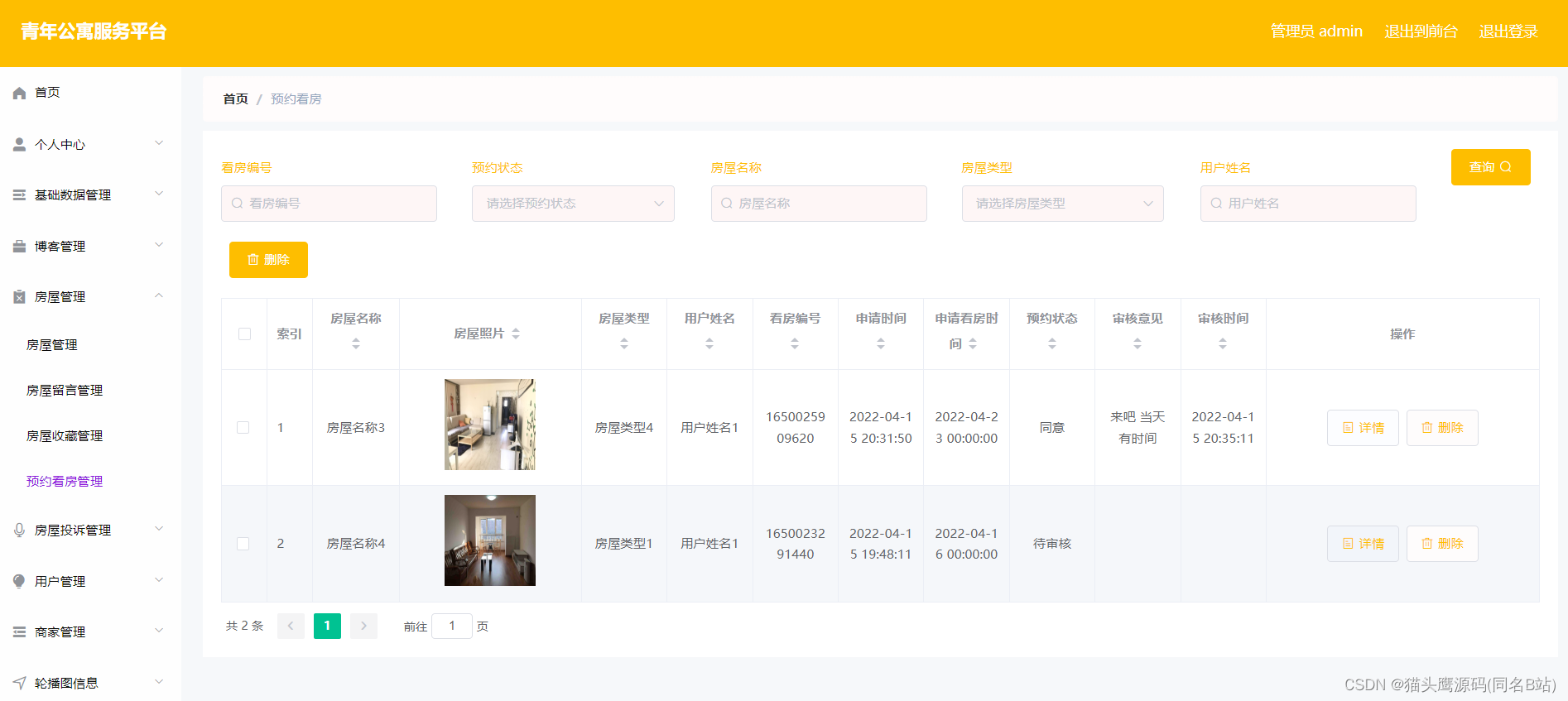
基于springboot+vue的青年公寓服务平台
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

Spring-ImportSelector接口功能介绍
ImportSelector接口是至spring中导入内部类或者外部类的核心接口,只需要其定义的方法内返回需要创建bean的class字符串就好了,比如:当我们引入一个外部share包,我们拿到里面的Class返回出去,就能得到这个bean,是多么神…...
YOLOv5如何训练自己的数据集
文章目录 前言1、数据标注说明2、定义自己模型文件3、训练模型4、参考文献 前言 本文主要介绍如何利用YOLOv5训练自己的数据集 1、数据标注说明 以生活垃圾数据集为例子 生活垃圾数据集(YOLO版)点击这里直接下载本文生活垃圾数据集 生活垃圾数据集组成&…...
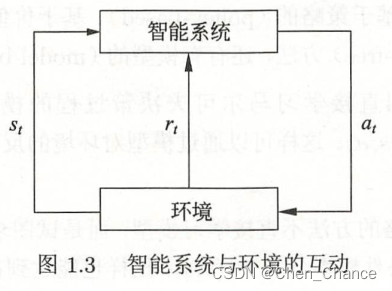
李航老师《统计学习方法》第1章阅读笔记
1.1 统计学习 统计学习的特点 统计学习:计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析 现在人们提及机器学习时,往往指统计机器学习,所以可以认为本书介绍的是机器学习方法 统计学习的对象 统计学习研究的对象是数据(data)…...

基于微信小程序的背单词学习激励系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言用户微信端的主要功能有:管理员的主要功能有:具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉…...
VScode调试复杂C/C++项目
以前都是用的VScode调试c/cpp的单个文件的编译和执行, 但是一遇到大型项目一般就用gdb了, gdb的调试效率和VScode差距还是比较大的, 但最近发现VScode其实也能调试复杂的cpp项目, 所以记录一下. 首先明确一下几点: 首先cpp文件需要经过编译, 生成可执行文件, 然后通过运行/调…...

【Hash表】字母异位词分组-力扣 49 题
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...
展示日志log4.properties
log4.properties 1.log4.properties 此时文件主要用于展示日志的输出的级别的信息。 # Set root category priority to INFO and its only appender to CONSOLE. #log4j.rootCategoryINFO, CONSOLE debug info warn error fatal log4j.rootCategoryinfo, CONSO…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
