【Acwing1027】方格取数(动态规划)题解
题目描述
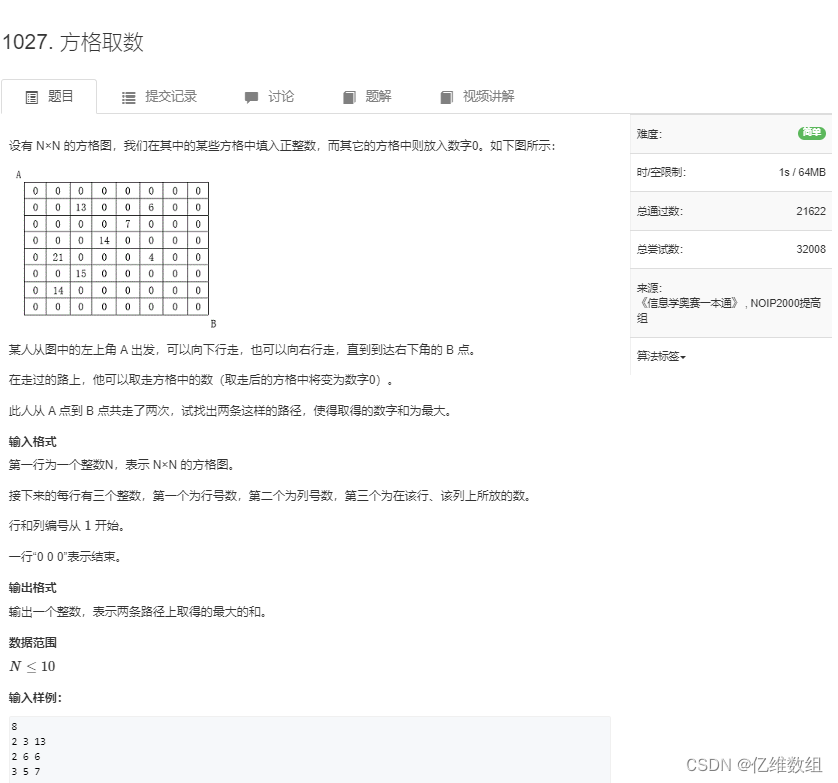
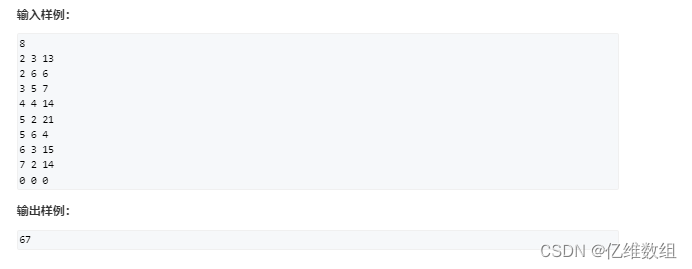
思路分析
错误思路:
贪心法,先走一次求出最大值,把走过的路上面的数值清零,然后用同样的方法再走一遍求最大值,然后让这两个最大值相加就是最后的结果。
很多人在看到这个题目的时候会有上面的思路,但实践告诉我们,有些数据用上述思路答案是错误的,这是为什么呢?
原因很简单:假设第一次走的时候,有多条路径s1,s2,......可以得到最大值,我们并不知道要选择哪一条,也就是说我们并不知道要把哪一条路上面的数清零,因为不同的选择会对第二次走的结果产生影响!!!
所以要使用其它思路,此处采用动态规划解决
起初,我们很容易想到用四维数组表示状态f[i1][j1][i2][j2]
但其实没有必要,因为我们只需要两条路“同时走”就可以了,也就是说我们可以设置一个维度代表(x,y方向上已经走的路径的和),这个表示为k,那么状态就可以降成三维:f[k][i1][i2]
下面对集合进行划分:
对于f[k][i1][i2],包含四部分:
第一部分是第一条路从上边走过来,第二条路是从上面走过来 f[k-1][i1-1][i2-1]+t
第二部分是第一条路从右边走过来,第二条路是从上面走过来 f[k-1][i1][i2-1]+t
第三部分是第一条路从上边走过来,第二条路是从右面走过来 f[k-1][i1-1][i2]+t
第四部分是第一条路从右边走过来,第二条路是从右面走过来 f[k-1][i1][i2]+t
那么这个t,怎么求,就要看i1和i2是否相同了,因为如果相同的话,再走到这里值已经清空了:
i1==i2 t=w[i1][k-i1]
i1!=i2 t=w[i1][k-i1]+w[i2][k-i2]
最后答案即为:f[n+n][n][n]
#include<iostream>
using namespace std;
const int N=15;
int f[N*2][N][N];
int w[N][N];
int n;
int main()
{scanf("%d",&n);int a,b,c;while(cin>>a>>b>>c,a||b||c)w[a][b]=c;for(int k=2;k<=n*2;k++){for(int i1=1;i1<=n;i1++){for(int i2=1;i2<=n;i2++){int j1=k-i1,j2=k-i2;if(j1>=1&&j1<=n&&j2>=1&&j2<=n){int t=w[i1][j1];if(i1!=i2)t+=w[i2][j2];int &x=f[k][i1][i2];x=max(x,f[k-1][i1-1][i2-1]+t);x=max(x,f[k-1][i1-1][i2]+t);x=max(x,f[k-1][i1][i2-1]+t);x=max(x,f[k-1][i1][i2]+t);}}}}cout<<f[2*n][n][n];return 0;
}相关文章:

【Acwing1027】方格取数(动态规划)题解
题目描述 思路分析 错误思路: 贪心法,先走一次求出最大值,把走过的路上面的数值清零,然后用同样的方法再走一遍求最大值,然后让这两个最大值相加就是最后的结果。 很多人在看到这个题目的时候会有上面的思路&#x…...

合并区间:解决区间重叠问题的高效算法
合并区间:解决区间重叠问题的高效算法 leetcode 56. 合并区间 合并区间是一个常见的编程问题,通常涉及到一组区间,你需要将重叠的区间合并成更大的区间。这篇博客将介绍这个问题的背景,然后解释一个高效的解决方案,同…...

万字总结HTML超文本标记语言
一、前言:什么是网页? 网站是指在因特网上根据一定的规则,使用 HTML 等制作的用于展示特定内容相关的网页集合。网页是网站中的一“页”,通常是 HTML 格式的文件,它要通过浏览器来阅读。 网页是构成网站的基本元素,它通常由图片、链接、文字、声音、视频等元素组成。通常…...
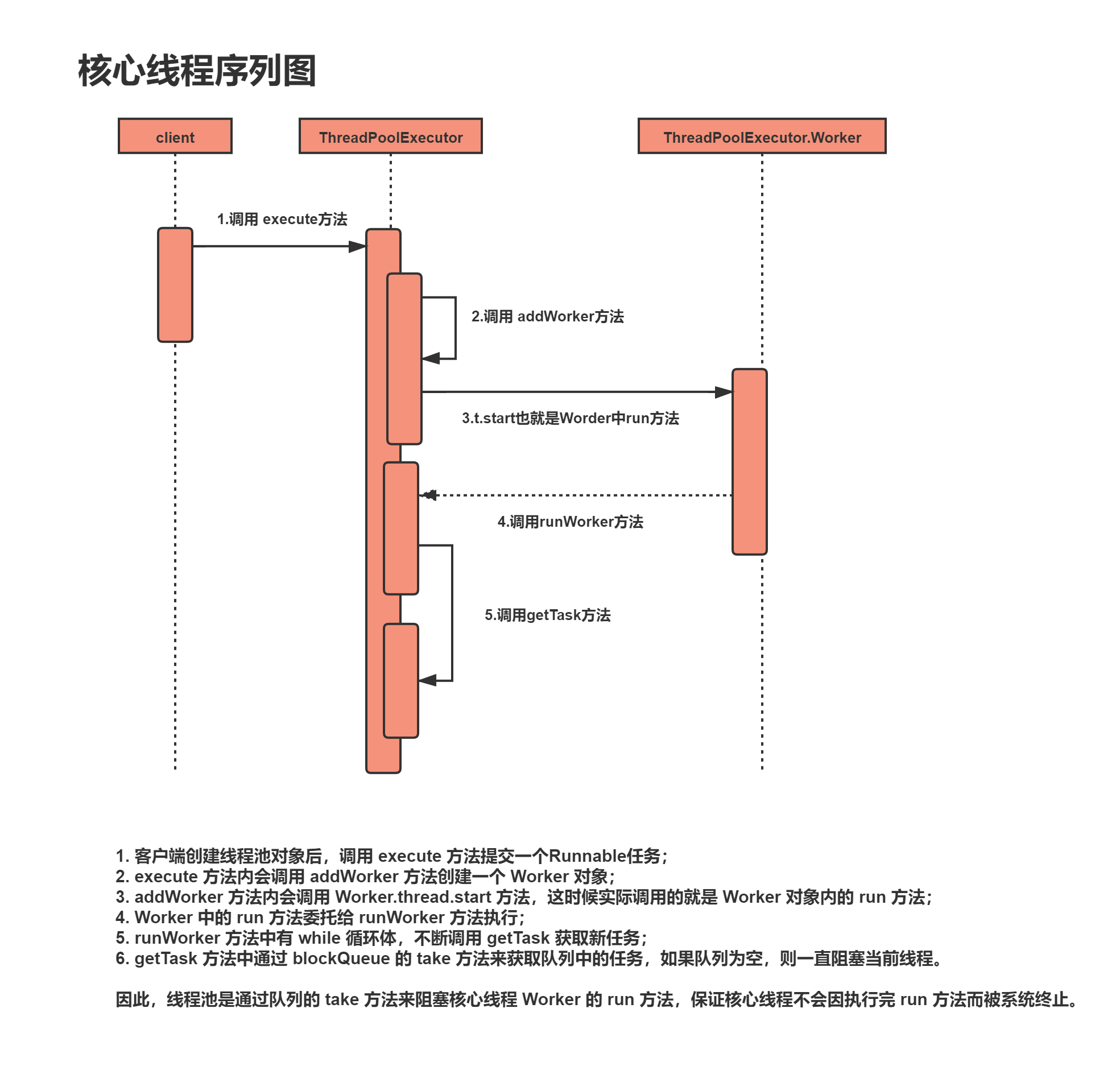
Java线程池是如何保证核心线程不被销毁的
来源: Java线程池是如何保证核心线程不被销毁的_朝 花 拾 夕的博客-CSDN博客 对于Java中 Thread 对象,同一个线程对象调用 start 方法后,会在执行完run 后走向终止(TERMINATED)状态,也就是说一个线程对象是不可以通过多…...

新课程标准培养学生“高考物理关键能力”的实践研究课题文献综述
目录 一、高考物理能力的要求与评估标准 二、高考物理关键能力的定义与内涵...

急救车工业路由器应用提升急救效率:车联网、数据采集与远程诊疗
急救车作为医院里医疗急救过程中的重要组成部分,在智慧医疗物联网领域中急救车应用4G工业路由器实现网络部署与数据采集,通过工业4G路由器能够实时采集到病患的生理数据、救护现场音频与视频、GPS定位以及车辆运行状态等重要信息。这些数据将被传输到医疗…...

【操作系统】聊聊CPU上下文切换实操
如何查看系统的上下文切换情况 上一篇文章我们说了过多的上下文切换,会把CPU时间消耗在寄存器、内核栈以及虚拟内存等数据的保存和恢复上,那么当出现系统的上下文切换过多的时候,我们如果通过监控指标查看呢。 vmstat 是一个常用的系统性能…...

【java】【SpringBoot】【四】原理篇 bean、starter、核心原理
目录 一、自动配置 1、bean加载方式(复习) 1.1 加载方式-xml方式生命bean 1.2 加载方式-xml注解方式声明bean 1.3 注解方式声明配置类 1.4 FactoryBean 1.5 proxyBeanMethod属性 1.6 使用Import注解导入 1.7 使用上下文对象在容器初始化完毕后注…...

【精品资源】Java毕业设计攻略:从选题到答辩,一站式指南
导读: Java毕业设计是计算机科学与技术专业学生展示其编程能力、问题解决能力和创新思维的重要环节。这篇博客将为您提供一站式的Java毕业设计攻略,帮助您从选题到答辩,顺利完成毕业设计。 一、选题阶段 寻找灵感: 探讨热门技术如…...
文件高效批量重命名,轻松重命名不同类型的文件名并隐藏编号
你是否曾经因为文件名混乱而感到困扰?你是否希望有一种方法可以快速、简单地管理你的文件名?如果你的答案是肯定的,那么我们的产品——文件重命名工具,将是你的完美解决方案! 首先我们要进入文件批量改名高手主页面&a…...

接口的定义与实现
一个c,代表类(class)。 一个c再加上两竖线,代表抽象类。 一个i,代表接口(interface)。 package com.mypackage.oop.demo12;//接口都需要有一个实现类 public interface UserService {//接口中定…...
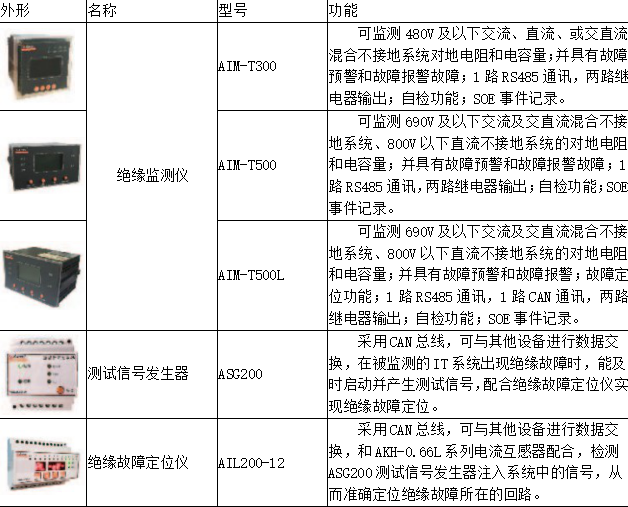
浅谈低压绝缘监测及定位系统在海上石油平台的研究与应用
安科瑞 华楠 摘要:海上石油平台低压系统与陆地电力系统有很大区别,其属于中性点绝缘系统,在出现单相接地故障时,系统允许带故障正常运行2 h,保证海上重要电气设备不会立即关停。现以渤海某海上平台为例,其…...
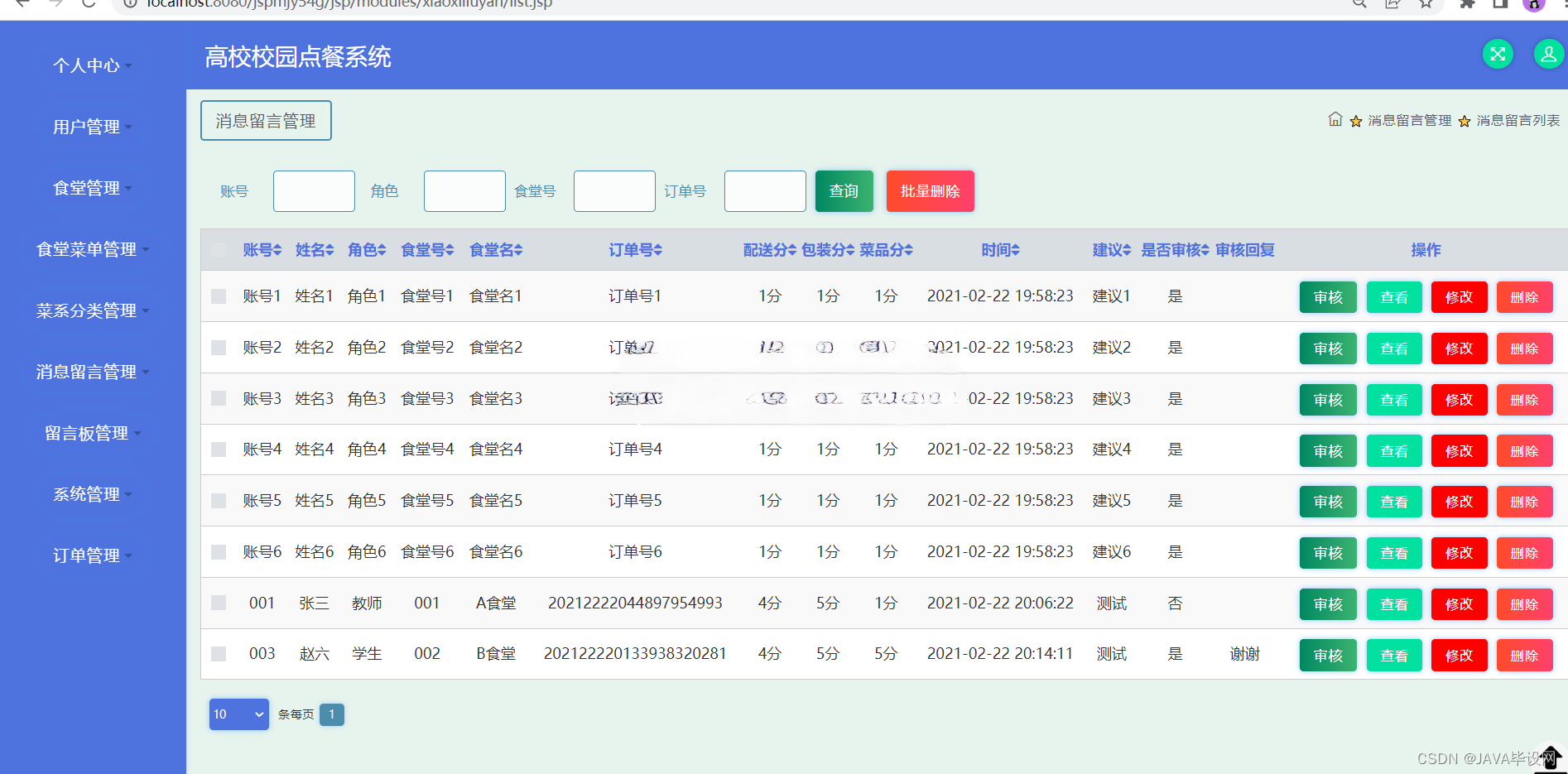
Java项目:SSM的食堂点餐系统
作者主页:Java毕设网 简介:Java领域优质创作者、Java项目、学习资料、技术互助 文末获取源码 一、相关文档 系统中的核心用户是系统管理员,管理员登录后,通过管理员菜单来管理后台系统。主要功能有:个人中心、用户管理…...
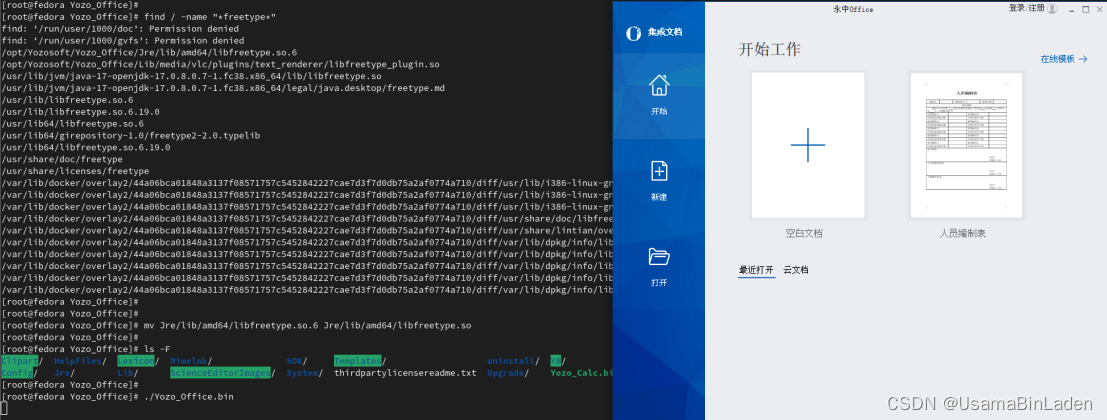
Linux桌面环境中应用程序无法启动图形交互界面
现象: 点击永中office或者金山office快捷图标无法启动对应的程序。 从命令行执行对应的程序则提示 按照提示安装组件 再次执行命令行程序 原因探析: /opt/Yozosoft/Yozo_Office/Yozo_Writer.bin: error while loading shared libraries: libgdk-x11-2.0.…...
jupyter notebook进不去指定目录怎么办?
首先激活你要使用的虚拟环境 刚开始是现在 (base) C:\Users\lenovo>目录下 直接输入你想进入的盘 (base) C:\Users\lenovo>e:此时再cd (base) C:\Users\lenovo>cd E:\tim\learn_pytorch 就可以进入了 安装3.4.1.15问题 已经有了最新python版本的虚拟环境&#…...

MySQL 高级(进阶) SQL 语句(二) -----存储过程
目录 1 存储过程 1.1 创建存储过程 1.2 调用存储过程 1.3 查看存储过程 1.4 存储过程的参数 1.5 修改存储过程 1.6 删除存储过程 2 条件语句 3 循环语句 1 存储过程 存储过程是一组为了完成特定功能的SQL语句集合。 存储过程在使用过程中是将常用或者复杂的工作预…...

机器学习第十三课--主成分分析PCA
一.高维数据 除了图片、文本数据,我们在实际工作中也会面临更多高维的数据。比如在评分卡模型构建过程中,我们通常会试着衍生出很多的特征,最后就得到上千维、甚至上完维特征;在广告点击率预测应用中,拥有几个亿特征也是常见的事…...

钉钉stream机器人-实操详细教程
支持事件订阅、机器人收消息、卡片回调等功能 优点: 配置简单,不依赖也不需要暴露公网IP,无需向公网开放端口 github官方链接:GitHub - open-dingtalk/dingtalk-stream-sdk-python: Python SDK for DingTalk Stream Mode API, Co…...
)
设计模式:访问者模式(C++实现)
访问者模式通过将对元素的操作与元素本身分离,使得可以在不修改元素类的情况下定义新的操作。 #include <iostream> #include <vector> #include <algorithm>// 前向声明 class ConcreteElementA; class ConcreteElementB;// 访问者接口 class V…...
Pygame中Sprite的使用方法6-6
4 重新绘制界面 每次碰撞发生后,程序界面需要重新绘制,代码如下所示。 screen.fill(WHITE) all_sprites_list.draw(screen) pygame.display.flip() 其中,screen表示程序的整个界面,将其绘制为白色背景;之后通过all_…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
