R语言RSTAN MCMC:NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据...
全文链接:http://tecdat.cn/?p=24456
如果你正在进行统计分析:想要加一些先验信息,最终你想要的是预测。所以你决定使用贝叶斯(点击文末“阅读原文”获取完整代码数据)。
相关视频
但是,你没有共轭先验。你可能会花费很长时间编写 Metropolis-Hastings 代码,优化接受率和提议分布,或者你可以使用 RStan。
Hamiltonian Monte Carlo(HMC)
HMC 是一种为 MH 算法生成提议分布的方法,该提议分布被接受的概率很高。具体算法过程请查看参考文献。
打个比方:
给粒子一些动量。
它在滑冰场周围滑行,大部分时间都在密度高的地方。
拍摄这条轨迹的快照为后验分布提供了一个建议样本。
然后我们使用 Metropolis-Hastings 进行校正。
NUTS采样器(No-U-turn Sampler)
HMC,像RWMH一样,需要对步骤的数量和大小进行一些调整。
No-U-Turn Sampler "或NUTs(Hoffman和Gelman(2014)),对这些进行了自适应的优化。
NUTS建立了一组可能的候选点,并在轨迹开始自相矛盾时立即停止。
Stan 的优点
可以产生高维度的提议,这些提议被接受的概率很高,而不需要花时间进行调整。
有内置的诊断程序来分析MCMC的输出。
在C++中构建,所以运行迅速,输出到R。
示例
如何使用 LASSO 构建贝叶斯线性回归模型。
构建 Stan 模型
数据:n、p、Y、X 先验参数,超参数
参数: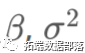
模型:高斯似然、拉普拉斯和伽玛先验。
输出:后验样本,后验预测样本。
数据
int<lwer=0> n;
vectr\[n\] y;
rel<loer=0> a;参数
vetor\[p+1\] beta;
real<lowr=0> siga;转换后的参数(可选)
vectr\[n\] liped;
lnpred = X*bea;模型
bta ~ dolexneial(0,w);
siga ~ gama(a,b);或没有矢量化,
for(i in 1:n){
y\[i\]~noral(X\[i,\]*beta,siga);
}生成的数量(可选)
vecor\[n\] yprict;
for(i in 1:n){
prdit\[i\] = nrmlrng(lnprd\[i\],siga);对后验样本的每一个元素都要评估一次这个代码。
职业声望数据集
这里我们使用职业声望数据集,它有以下变量
教育:职业在职者的平均教育程度,年。
收入:在职者的平均收入,元。
女性:在职者中女性的百分比。
威望:Pineo-Porter的职业声望得分,来自一项社会调查。
普查:人口普查的职业代码。
类型:职业的类型
bc: 蓝领
prof: 专业、管理和技术
wc: 白领
在R中运行
library(rstan)
stan(file="byLASO",iter=50000)在3.5秒内运行25000次预热和25000次采样。
第一次编译c++代码,所以可能需要更长的时间。
绘制后验分布图
par(mrow=c(1,2))
plot(denty(prs$bea)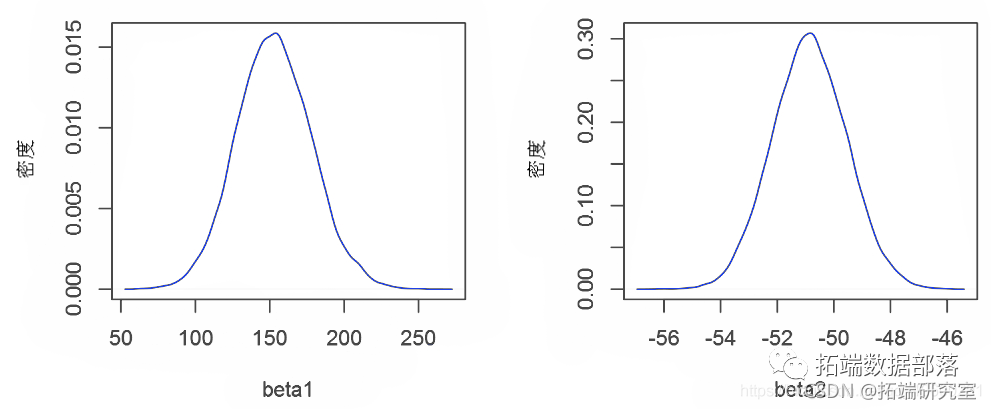
预测分布
plot(density)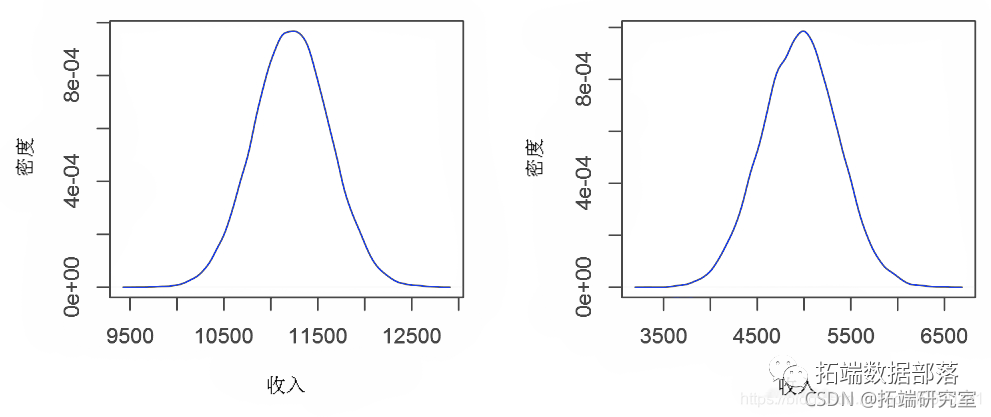
点击标题查阅往期内容

R语言贝叶斯MCMC:用rstan建立线性回归模型分析汽车数据和可视化诊断

左右滑动查看更多

01
02
03

04
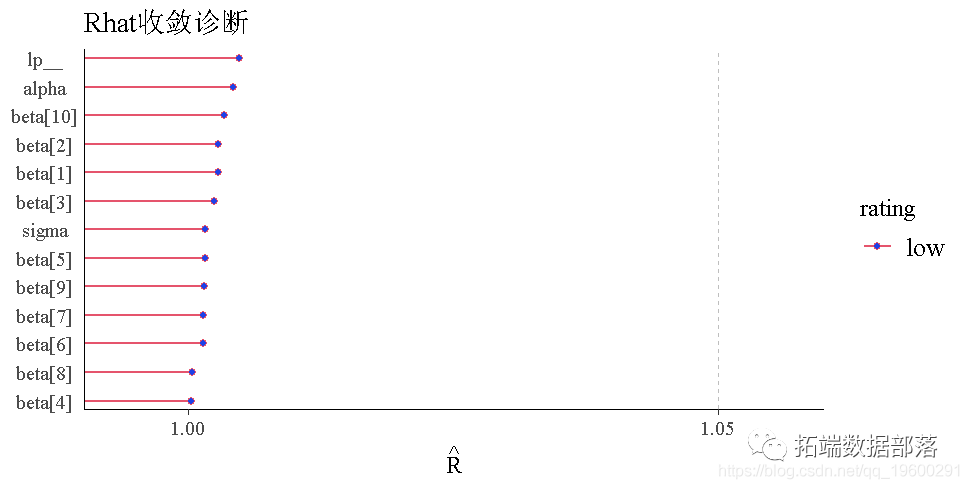
链诊断
splas\[\[1\]\[1:5,\]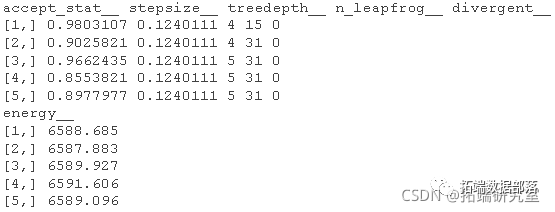
链诊断
trac("beta" )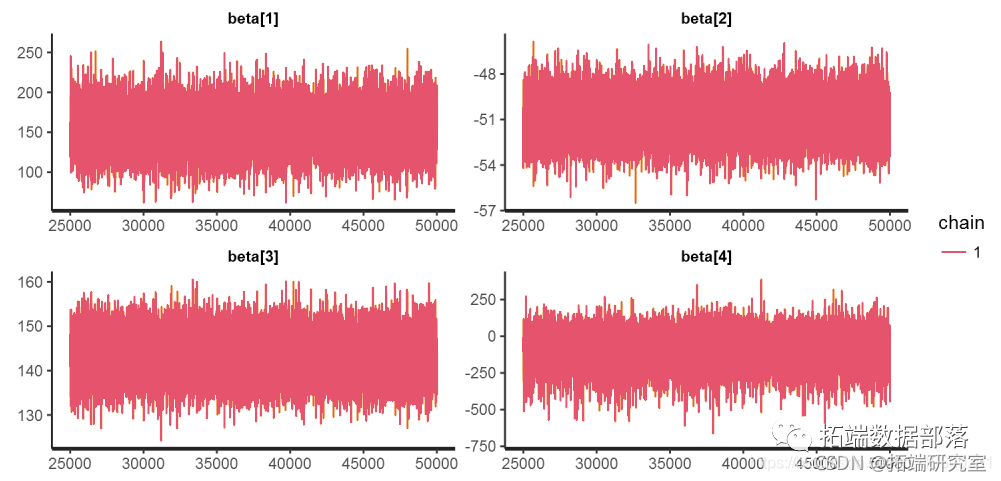
链诊断
pa(pars="beta")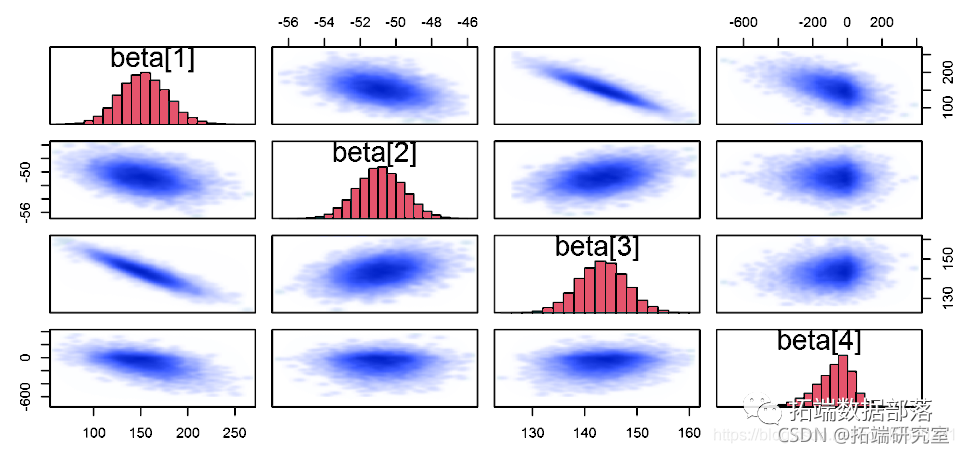
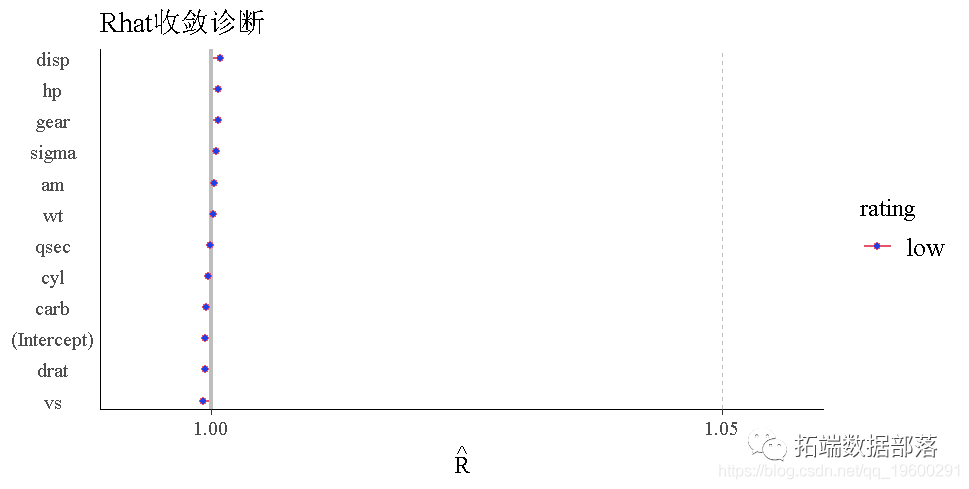
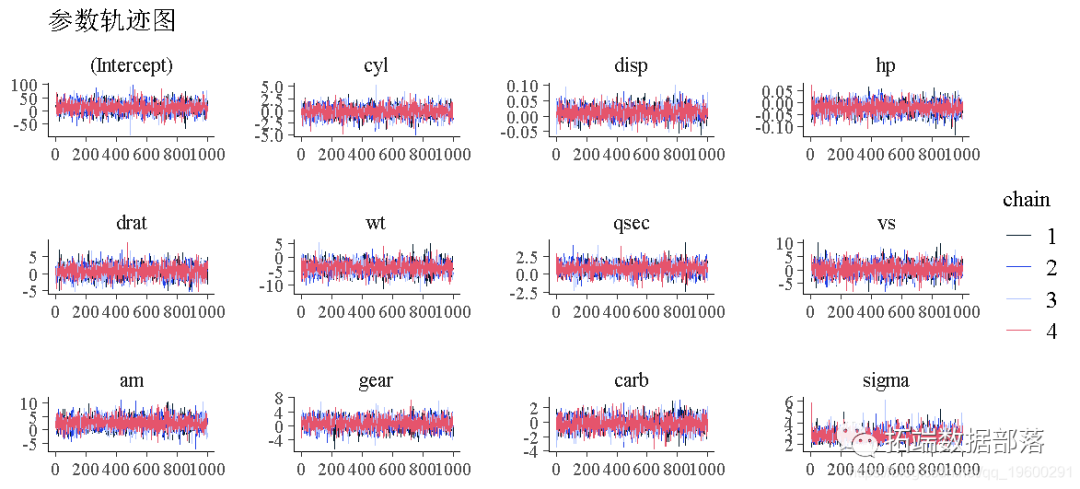
更多链诊断
Stan 还可以从链中提取各种其他诊断,如置信区间、有效样本量和马尔可夫链平方误差。
链的值与各种链属性、对数似然、接受率和步长之间的比较图。
Stan 出错
stan使用的步骤太大。
可以通过手动增加期望的平均接受度来解决。
adapt_delta,高于其默认的0.8
stan(cntl = list(datta = 0.99, mxrh = 15))这会减慢你的链的速度,但可能会产生更好的样本。
自制函数
Stan 也兼容自制函数。
如果你的先验或似然函数不标准,则很有用。
model {
beta ~ doubexp(0,w);
for(i in 1:n){
logprb(‐0.5*fs(1‐(exp(normalog(
siga))/yde));
}
}结论
不要浪费时间编码和调整 RWMH.
Stan 运行得更快,会自动调整,并且应该会产生较好的样本。
参考文献
Alder, Berni J, and T E Wainwright. 1959. “Studies in Molecular Dynamics. I. General Method.” The Journal of Chemical Physics 31 (2). AIP: 459–66.
Hoffman, Matthew D, and Andrew Gelman. 2014. “The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo.” Journal of Machine Learning Research 15 (1): 1593–1623.

点击文末“阅读原文”
获取全文完整资料。
本文选自《R语言RSTAN MCMC:NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据》。


点击标题查阅往期内容
R语言贝叶斯MCMC:用rstan建立线性回归模型分析汽车数据和可视化诊断
【视频】马尔可夫链蒙特卡罗方法MCMC原理与R语言实现|数据分享
R语言实现MCMC中的Metropolis–Hastings算法与吉布斯采样
R语言贝叶斯METROPOLIS-HASTINGS GIBBS 吉布斯采样器估计变点指数分布分析泊松过程车站等待时间
R语言马尔可夫MCMC中的METROPOLIS HASTINGS,MH算法抽样(采样)法可视化实例
python贝叶斯随机过程:马尔可夫链Markov-Chain,MC和Metropolis-Hastings,MH采样算法可视化
Python贝叶斯推断Metropolis-Hastings(M-H)MCMC采样算法的实现
Metropolis Hastings采样和贝叶斯泊松回归Poisson模型
Matlab用BUGS马尔可夫区制转换Markov switching随机波动率模型、序列蒙特卡罗SMC、M H采样分析时间序列
R语言RSTAN MCMC:NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据
R语言BUGS序列蒙特卡罗SMC、马尔可夫转换随机波动率SV模型、粒子滤波、Metropolis Hasting采样时间序列分析
R语言Metropolis Hastings采样和贝叶斯泊松回归Poisson模型
R语言贝叶斯MCMC:用rstan建立线性回归模型分析汽车数据和可视化诊断
R语言贝叶斯MCMC:GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例
R语言贝叶斯Poisson泊松-正态分布模型分析职业足球比赛进球数
R语言用Rcpp加速Metropolis-Hastings抽样估计贝叶斯逻辑回归模型的参数
R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病
R语言中贝叶斯网络(BN)、动态贝叶斯网络、线性模型分析错颌畸形数据
R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归
Python贝叶斯回归分析住房负担能力数据集
R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析
Python用PyMC3实现贝叶斯线性回归模型
R语言用WinBUGS 软件对学术能力测验建立层次(分层)贝叶斯模型
R语言Gibbs抽样的贝叶斯简单线性回归仿真分析
R语言和STAN,JAGS:用RSTAN,RJAG建立贝叶斯多元线性回归预测选举数据
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言贝叶斯线性回归和多元线性回归构建工资预测模型
R语言贝叶斯推断与MCMC:实现Metropolis-Hastings 采样算法示例
R语言stan进行基于贝叶斯推断的回归模型
R语言中RStan贝叶斯层次模型分析示例
R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化
R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型
WinBUGS对多元随机波动率模型:贝叶斯估计与模型比较
R语言实现MCMC中的Metropolis–Hastings算法与吉布斯采样
R语言贝叶斯推断与MCMC:实现Metropolis-Hastings 采样算法示例
R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化
视频:R语言中的Stan概率编程MCMC采样的贝叶斯模型
R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计

![]()

相关文章:

R语言RSTAN MCMC:NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据...
全文链接:http://tecdat.cn/?p24456 如果你正在进行统计分析:想要加一些先验信息,最终你想要的是预测。所以你决定使用贝叶斯(点击文末“阅读原文”获取完整代码数据)。 相关视频 但是,你没有共轭先验。你…...
【PowerShell】PowerShell的Core版本的额外配置
在PowerShell 7.1 安装完成后,默认情况下打开PowerShell 会直接进入到系统内置的PowerShell,如果希望通过远程连接或者PowerShell Web Access 进入到PowerShell 7环境的界面,就需要进行环境的再配置才能实现PowerShell 7.1 的环境连接。需要为外部的环境提供连接的话需要按照…...

数据结构----链式栈
目录 前言 链式栈 操作方式 1.存储结构 2.初始化 3.创建节点 4.判断是否满栈 5.判断是否空栈 6.入栈 7.出栈 8.获取栈顶元素 9.遍历栈 10.清空栈 完整代码 前言 前面我们学习过了数组栈的相关方法,(链接:线性表-----栈(栈…...

实在智能携手40+央企,探索财务大模型及数智化实践与应用
“这次培训给我一个最大的感触就是,过去以为AI智能化、大模型技术是很高深的事情。但现在,我们通过RPA等数字化工具,自主根据自己的工作岗位,完成业务自动化流程的开发和设计。AI技术没有想象中的那么难入门。” 这是一位参加了“…...
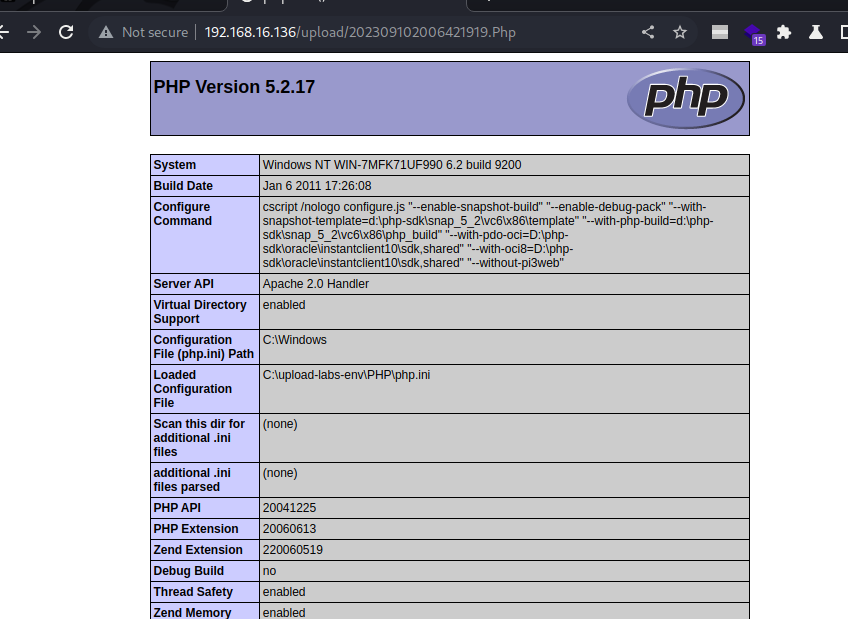
upload-labs文件上传1-5关
第一关 编写一句话木马1.php,编写完成后将后缀名修改为png 将1.png上传,上传时使用bp抓包 抓包后将后缀名修改为png 连接蚁剑 第二关 上传1.php,显示文件类型不正确 使用bp抓包发送重发器,修改文件后缀名后点击发送,…...

git的基本使用
查看当前分支 git branch //查看本地分支 git branch -a // 查看本地和远程的分支切分支 git checkout -b 分支的名字从当前分支切换到其他分支 拉取远程分支到本地 拉取远程develop分支代码到本地develop分支 git checkout -b develop origin/developgit merge B分支合并…...

Mac台式电脑内存清理方法教程
对于一些小白用户,如果觉得以上的清理方法比较复杂却又想要更好的优化Mac电脑内存,专业的系统清理软件是一个不错的选择。比起花几个小时时间浏览文件夹、删除临时文件、缓存和卸载残留。Cleanmymac X,只需单击几下即可完成所有内存清理工作&…...

FL Studio怎么破解?2023年最新FL Studio 21图文安装激活教程?FL 21中文版下载 v21.1.1.3750 汉化 版
fl studio21中文解锁特别破解版是一款功能强大的编曲软件,也就是众所熟知的水果软件。它可以编曲、剪辑、录音、混音,让您的计算机成为全功能录音室。除此之外,这款软件功能非常强大,为用户提供了许多音频处理工具,包含…...

Zookeeper高级_四字命令
之前使用stat命令来验证ZooKeeper服务器是否启动成功,这里的stat命令就是ZooKeeper 中最为典型的命令之一。ZooKeeper中有很多类似的命令,它们的长度通常都是4个英文字母,因此我们称之为“四字命令”。 添加配置 vim zoo.cfg 4lw.commands…...

/usr/bin/ld: cannot find -lmysqlcllient
文章目录 1. question: /usr/bin/ld: cannot find -lmysqlcllient2. solution 1. question: /usr/bin/ld: cannot find -lmysqlcllient 2. solution 在 使用编译命令 -lmysqlclient时,如果提示这个信息。 先确认一下 有没有安装mysql-devel 执行如下命令 yum inst…...
折线图geom_line()参数选项
往期折线图教程 图形复现| 使用R语言绘制折线图折线图指定位置标记折线图形状更改 | 绘制动态折线图跟着NC学作图 | 使用python绘制折线图 前言 我们折线的专栏推出一段时间,但是由于个人的原因,一直未进行更新。那么今天,我们也参考《R语…...

百度SEO优化基本原理(掌握SEO基础,提高网站排名)
随着互联网的迅速发展,越来越多的企业开始意识到网站优化的重要性,其中百度SEO优化是企业不可忽视的一项工作。本文将介绍百度SEO优化的基本概念、步骤、原理、解决方法和提升网站标题优化的方法。蘑菇号-www.mooogu.cn 百度SEO优化是指针对百度搜索引擎…...
)
2023 ICPC 网络赛 第一场 部分题解 (待完善)
D Transitivity 题解: 根据题意可以推出结论: 如果存在连通块,那么这个连通块要满足条件,必然是满连通块. 一共有两种情况 1. 存在一个连通块不是满连通块 设cnt表示连通块的节点个数, num表示连通块边的个数 一个连通块的贡献 cnt*(cnt-1)/2 - num; 那么最终答案 连…...

Hadoop的HDFS高可用方案
一、Hadoop高可用简介 Hadoop 高可用 (High Availability) 分为 HDFS 高可用和 YARN 高可用,两者的实现基本类似,但 HDFSNameNode 对数据存储及其一致性的要求比 YARN ResourceManger 高得多,所以它的实现也更加复杂 1、HDFS系统高可用简介…...

【计算机基础】让我们重新认识一下Visual Stduio及其操作,知识点汇总!!
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...

使用Node构建私人代理池
在进行大规模数据采集时,经常会遇到网站反爬虫机制导致爬虫被封的问题。为了解决这个困扰,本文将向大家介绍如何利用Node.js构建私人代理池,提供稳定的代理,实现高效、可靠的爬虫操作。跟随本文一起学习,拥有解封爬虫的…...

2023年“羊城杯”网络安全大赛 决赛 AWDP [Break+Fix] Web方向题解wp 全
终于迎来了我的第一百篇文章。 这次决赛赛制是AWDP。BreakFix,其实就是CTFFix,Fix规则有点难崩。Break和Fix题目是一样的。 总结一下:败北,还是太菜了得继续修炼一下。 一、Break ezSSTI 看到是SSTI,焚靖直接一把梭…...
如何用好免费的ChatGPT
如何用好免费的ChatGPT 前言ChatGPT使用入口在线体验地址:点我体验 ChatGPT介绍ChatGPT初级使用技巧初级使用技巧:清晰明了的问题表达 ChatGPT中级使用语法中级使用语法:具体化问题并提供背景信息 ChatGPT高级使用高级使用:追问、…...

golang 实现带令牌限流的JWT demo
demo里提供了三个接口,认证取token,刷新token,获取信息,token过期前也会在header里写上新token(便于客户端更换) package mainimport ("fmt""net/http""sync""time&qu…...
ajax请求)
【web开发】9、Django(4)ajax请求
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、Ajax是什么?二、使用步骤二、订单管理 提示:以下是本篇文章正文内容,下面案例可供参考 一、Ajax是什么? Ajax&…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
