辨析常见的医学数据分析(相关性分析回归分析)
目录
1 常见的三种分类结果?
2 什么是相关性分析?
相关性分析的结果怎么看?
3 什么是回归分析?
1)前提
2)常见的回归模型
4 对于存在对照组实验的医学病例如何分析?
1)卡方检验
2)Fisher 精确概率法
为了更好理解下述辨析,假设有一份关于膝关节骨性关节炎的数据:(注:这里仅为示意,没有任何医学借鉴含义)
| 患者编号 | 年龄 | 性别 | BMI | 是否为关节炎 | 关节炎严重程度 | 软骨损伤类型 |
| 001 | 60 | 0 | 23.4 | 1-是 | 轻度 | 1-软骨软化 |
| 002 | 56 | 1 | 26.1 | 1-是 | 中度 | 2-软骨裂隙 |
| 003 | 64 | 0 | 25.5 | 1-是 | 轻度 | 3-局灶性缺损 |
| 004 | 63 | 0 | 26.8 | 1-是 | 重度 | 4-弥漫性变薄 |
| *软骨损伤类型的分类方式参考了文献《Deep Learning Approach for Evaluating Knee MR Images: Achieving High Diagnostic Performance for Cartilage Lesion Detection》 | ||||||
1 常见的三种分类结果?
二元分类:e.g. 是/否 为关节炎
多元有序分类:疾病严重程度的分级(分类结果有序且等差,e.g.轻度、中度、重度依次等差递增)
多元无序分类:疾病的种类,e.g.肺癌、乳腺癌、胃癌,这里如软骨损伤的类型。这些分类结果没有等级上的关系,都是并列关系的诊断结果。
2 什么是相关性分析?
两个变量之间是否存在相关性及计算相关程度的大小。
主要分为两类:线性相关 && 秩相关
| 线性相关分析 | 秩相关分析 | |
| 类型 | 参数检验 | 非参数检验 |
| 数据需求 | 双定量变量(连续型数值变量),均满足正态分布 | 定量或等级变量,即至少有一个变量为偏态分布或等级变量 |
| 分析方法 | Pearson相关 | Spearman相关 |
| 相关系数 | Pearson相关系数,r | Spearman相关系数, |
| p值与结论 | p<0.05:两变量总体线性相关 | p<0.05:两变量总体相关 |
| r值与结论 | |r| > 0.8,两变量存在极强的相关; 0.6 < |r| < 0.8,强相关; 0.4 < |r| < 0.6,中等相关; |r| < 0.4,弱相关。 | |
相关性分析的结果怎么看?
①先看显著性p值,(变量间是否存在显著性影响的关系)只有存在显著性相关(即 p < 0.05),再分析r值;(若不存在相关性,考虑筛选别的影响因子纳入表格)
②看相关性系数r值,判断变量间是显著强相关/中等相关/弱相关。
3 什么是回归分析?
如果说,相关性分析是看自变量对因变量是否有影响,那么,回归分析是看自变量如何影响因变量的模型拟合。
相关性分析基于两两变量直接的关系探究;而回归分析一次性纳入了所有可能相关的变量,模拟真实的环境以找到真正有独立影响性的因素,并得到这些因素是如何作用的。
1)前提
建立回归模型的多变量不能存在共线性的关系(如,BMI是由身高与体重的线性计算公式得到的,那么建立模型时就不能同时纳入BMI和体重两个自变量)
2)常见的回归模型
| 二元Logistic回归 | 适用于二元分类(是否发生疾病) |
| 多元有序Logistic回归 | 适用于多元有序分类 |
| 多元无序Logistic回归 | 适用于多元无序分类 |
| Cox回归 | 含有“时间数据”的二元Logistic回归 (疾病发生的速度) |
4 对于存在对照组实验的医学病例如何分析?
1)卡方检验
卡方检验进行分析的目的是比较差异性。
建立了两组假设:①零假设:观察组和对照组的作用结果一致。(如,某新药物【观察组】和常规药物【对照组】的疗效一致。)
②备选假设:观察组和对照组的作用结果显著不一致。(如,想要证实新药物的疗效更好。)
卡方检验的p值<0.05,则拒绝零假设,接受备选假设;反之,接受零假设。
参考:卡方(χ2),四格表应用条件,理论频数_weixin_34307464的博客-CSDN博客,由于基于卡方分布模型,使用卡方检验的前提:①样本总量>40;②四格表的理论频数≠0并且理论频数<5的样本不超过总样本数的20%。
2)Fisher 精确概率法
对于小样本,或四格表的理论频数=0的情况,使用Fisher 精确概率法。
目的: 以超几何分布为理论模型,用来检验一次随机实验的结果是否支持对于某个随机实验的假设,当测试结果出现小概率事件则认定原有假设不被支持。
同样地,Fisher 检验的p值<0.05,则拒绝零假设。
与卡方检验的区别在于:在实际计算当中分为单边检验(即超几何检验)和双边检测。实际应用中,Fisher检验前先有一个预期,如:想要得到新药比常规药的有效概率更大,则选择Fisher检验的“大于”的单侧;若只是想要得到新药与常规药的有效性有差异,则选择Fisher双边检测。
相关文章:
辨析常见的医学数据分析(相关性分析回归分析)
目录 1 常见的三种分类结果? 2 什么是相关性分析? 相关性分析的结果怎么看? 3 什么是回归分析? 1)前提 2)常见的回归模型 4 对于存在对照组实验的医学病例如何分析? 1)卡方检验…...

SpringBoot项目中只执行一次的任务写法
SpringBoot项目中只执行一次的任务写法 有时候我们需要进行初始化工作,就说明只要进行一次的工作,那么,在Springboot项目中如何做到任务只进行一次呢 利用定时任务 在Spring Boot项目中,你可以使用Spring框架提供的Scheduled注解…...

TCK、TMS、TDI、TDO的含义
这四个信号是JTAG(Joint Test Action Group)界面的一部分。JTAG是一种用于测试和验证集成电路和印刷电路板的技术,也用于进行设备编程和调试。这四个信号分别是: TCK (Test Clock): 意义:测试时钟ÿ…...

R语言RSTAN MCMC:NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据...
全文链接:http://tecdat.cn/?p24456 如果你正在进行统计分析:想要加一些先验信息,最终你想要的是预测。所以你决定使用贝叶斯(点击文末“阅读原文”获取完整代码数据)。 相关视频 但是,你没有共轭先验。你…...
【PowerShell】PowerShell的Core版本的额外配置
在PowerShell 7.1 安装完成后,默认情况下打开PowerShell 会直接进入到系统内置的PowerShell,如果希望通过远程连接或者PowerShell Web Access 进入到PowerShell 7环境的界面,就需要进行环境的再配置才能实现PowerShell 7.1 的环境连接。需要为外部的环境提供连接的话需要按照…...

数据结构----链式栈
目录 前言 链式栈 操作方式 1.存储结构 2.初始化 3.创建节点 4.判断是否满栈 5.判断是否空栈 6.入栈 7.出栈 8.获取栈顶元素 9.遍历栈 10.清空栈 完整代码 前言 前面我们学习过了数组栈的相关方法,(链接:线性表-----栈(栈…...

实在智能携手40+央企,探索财务大模型及数智化实践与应用
“这次培训给我一个最大的感触就是,过去以为AI智能化、大模型技术是很高深的事情。但现在,我们通过RPA等数字化工具,自主根据自己的工作岗位,完成业务自动化流程的开发和设计。AI技术没有想象中的那么难入门。” 这是一位参加了“…...
upload-labs文件上传1-5关
第一关 编写一句话木马1.php,编写完成后将后缀名修改为png 将1.png上传,上传时使用bp抓包 抓包后将后缀名修改为png 连接蚁剑 第二关 上传1.php,显示文件类型不正确 使用bp抓包发送重发器,修改文件后缀名后点击发送,…...

git的基本使用
查看当前分支 git branch //查看本地分支 git branch -a // 查看本地和远程的分支切分支 git checkout -b 分支的名字从当前分支切换到其他分支 拉取远程分支到本地 拉取远程develop分支代码到本地develop分支 git checkout -b develop origin/developgit merge B分支合并…...

Mac台式电脑内存清理方法教程
对于一些小白用户,如果觉得以上的清理方法比较复杂却又想要更好的优化Mac电脑内存,专业的系统清理软件是一个不错的选择。比起花几个小时时间浏览文件夹、删除临时文件、缓存和卸载残留。Cleanmymac X,只需单击几下即可完成所有内存清理工作&…...

FL Studio怎么破解?2023年最新FL Studio 21图文安装激活教程?FL 21中文版下载 v21.1.1.3750 汉化 版
fl studio21中文解锁特别破解版是一款功能强大的编曲软件,也就是众所熟知的水果软件。它可以编曲、剪辑、录音、混音,让您的计算机成为全功能录音室。除此之外,这款软件功能非常强大,为用户提供了许多音频处理工具,包含…...

Zookeeper高级_四字命令
之前使用stat命令来验证ZooKeeper服务器是否启动成功,这里的stat命令就是ZooKeeper 中最为典型的命令之一。ZooKeeper中有很多类似的命令,它们的长度通常都是4个英文字母,因此我们称之为“四字命令”。 添加配置 vim zoo.cfg 4lw.commands…...

/usr/bin/ld: cannot find -lmysqlcllient
文章目录 1. question: /usr/bin/ld: cannot find -lmysqlcllient2. solution 1. question: /usr/bin/ld: cannot find -lmysqlcllient 2. solution 在 使用编译命令 -lmysqlclient时,如果提示这个信息。 先确认一下 有没有安装mysql-devel 执行如下命令 yum inst…...
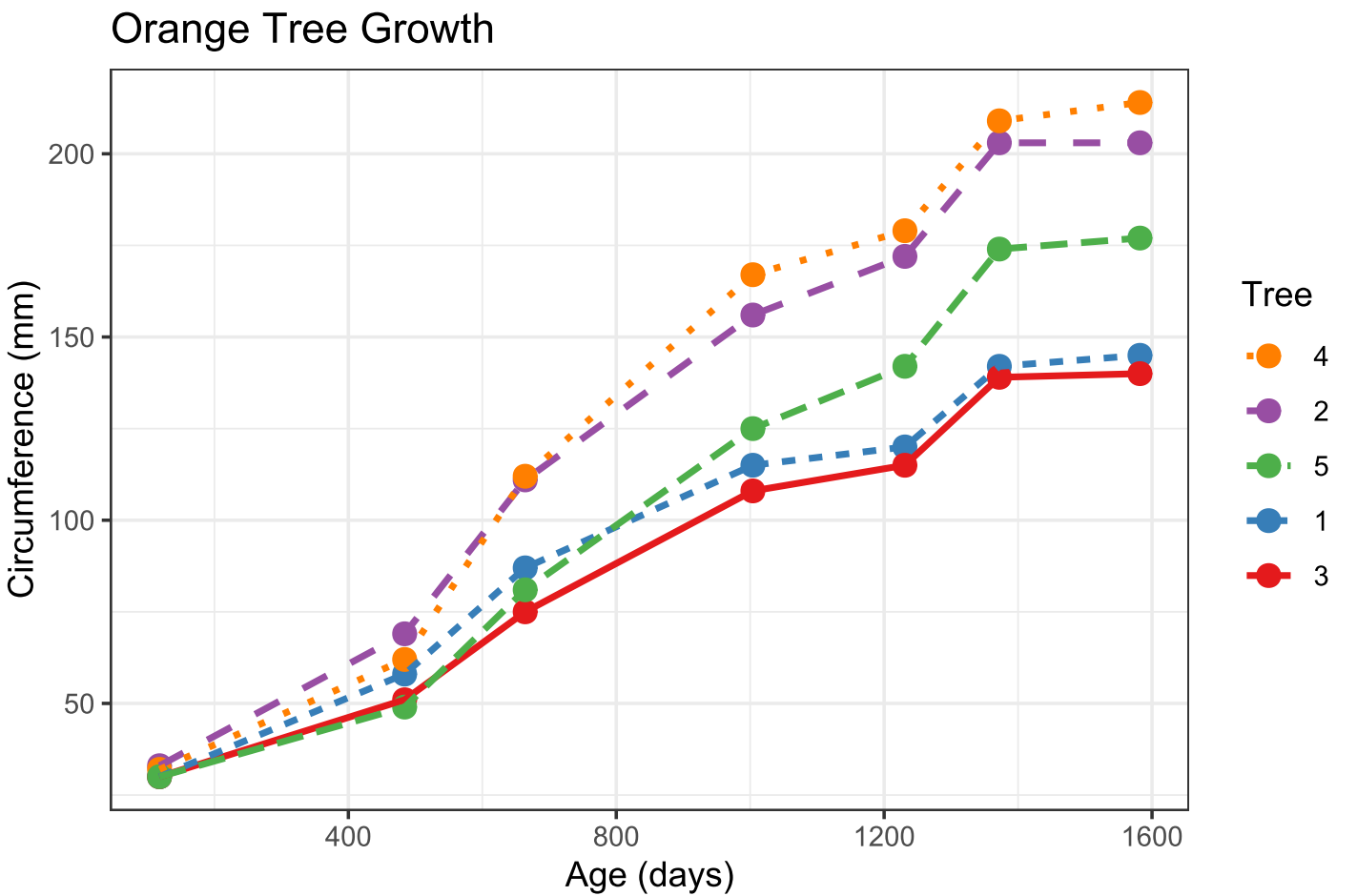
折线图geom_line()参数选项
往期折线图教程 图形复现| 使用R语言绘制折线图折线图指定位置标记折线图形状更改 | 绘制动态折线图跟着NC学作图 | 使用python绘制折线图 前言 我们折线的专栏推出一段时间,但是由于个人的原因,一直未进行更新。那么今天,我们也参考《R语…...

百度SEO优化基本原理(掌握SEO基础,提高网站排名)
随着互联网的迅速发展,越来越多的企业开始意识到网站优化的重要性,其中百度SEO优化是企业不可忽视的一项工作。本文将介绍百度SEO优化的基本概念、步骤、原理、解决方法和提升网站标题优化的方法。蘑菇号-www.mooogu.cn 百度SEO优化是指针对百度搜索引擎…...
)
2023 ICPC 网络赛 第一场 部分题解 (待完善)
D Transitivity 题解: 根据题意可以推出结论: 如果存在连通块,那么这个连通块要满足条件,必然是满连通块. 一共有两种情况 1. 存在一个连通块不是满连通块 设cnt表示连通块的节点个数, num表示连通块边的个数 一个连通块的贡献 cnt*(cnt-1)/2 - num; 那么最终答案 连…...

Hadoop的HDFS高可用方案
一、Hadoop高可用简介 Hadoop 高可用 (High Availability) 分为 HDFS 高可用和 YARN 高可用,两者的实现基本类似,但 HDFSNameNode 对数据存储及其一致性的要求比 YARN ResourceManger 高得多,所以它的实现也更加复杂 1、HDFS系统高可用简介…...

【计算机基础】让我们重新认识一下Visual Stduio及其操作,知识点汇总!!
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...

使用Node构建私人代理池
在进行大规模数据采集时,经常会遇到网站反爬虫机制导致爬虫被封的问题。为了解决这个困扰,本文将向大家介绍如何利用Node.js构建私人代理池,提供稳定的代理,实现高效、可靠的爬虫操作。跟随本文一起学习,拥有解封爬虫的…...

2023年“羊城杯”网络安全大赛 决赛 AWDP [Break+Fix] Web方向题解wp 全
终于迎来了我的第一百篇文章。 这次决赛赛制是AWDP。BreakFix,其实就是CTFFix,Fix规则有点难崩。Break和Fix题目是一样的。 总结一下:败北,还是太菜了得继续修炼一下。 一、Break ezSSTI 看到是SSTI,焚靖直接一把梭…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
