Leetcode算法入门与数组丨6. 数组双指针、滑动窗口
文章目录
- 1 双指针基础知识
- 1.1 双指针简介
- 1.2 左右指针(对撞指针)
- 1.3 快慢指针
- 1.4 分离双指针
- 2 滑动窗口基础知识
- 2.1 滑动窗口算法介绍
- 2.2 滑动窗口适用范围
- 2.3 固定长度滑动窗口
- 2.4 不固定长度滑动窗口
1 双指针基础知识
1.1 双指针简介
双指针(Two Pointers) 是一种常用的算法技巧,通常用于在数组或链表中进行遍历或搜索。它使用两个指针在不同的位置上移动,以解决特定的问题。
双指针常见的应用场景包括:
- 快慢指针:两个指针方向相同,但是使用两个指针以不同的速度遍历链表,用于解决链表中的环检测、链表中点、链表倒数第k个节点等问题。
- 左右指针(对撞指针):在有序数组中,使用两个指针从数组的两端向中间移动,以解决查找目标值、两数之和、三数之和等问题。
- 分离双指针:两个指针分别属于不同的数组/链表。
双指针算法通常具有较低的时间复杂度,并且可以在一次遍历中完成任务,因此在很多问题中都有很好的应用。
1.2 左右指针(对撞指针)
左右指针(Left and Right Pointers)是双指针算法中的一种常见技巧。它通常用于在有序数组或字符串中查找目标值、寻找满足某种条件的子序列等问题。
左右指针的基本思想是,使用两个指针分别指向数组或字符串的左右两端,然后根据问题的要求,通过移动指针的位置来逼近或搜索目标。
基本步骤
- 两个指针 l e f t left left 和 r i g h t right right。 l e f t left left 指向序列第一个元素( l e f t = 0 left=0 left=0 ), r i g h t right right 指向序列最后一个元素( r i g h t = l e n ( n u m s ) − 1 right=len(nums)-1 right=len(nums)−1 )。
- 循环体中将左右指针相向移动,当满足一定条件时,将左指针右移( l e f t + = 1 left += 1 left+=1 )。当满足另外一定条件时,将右指针左移( r i g h t + = 1 right+= 1 right+=1 )。
- 直到两个指针相撞( l e f t = r i g h t left=right left=right ),或者满足其他要求的特殊条件时,跳出循环体。
伪代码模板
left, right = 0, len(nums) - 1while left < right:if 满足要求的特殊条件:return 符合条件的值 elif 一定条件 1:left += 1elif 一定条件 2:right -= 1return 没找到 或 找到对应值
适用范围
-
有序数组或有序链表:左右指针可以在有序数组或有序链表中进行查找、搜索、比较等操作。通过左右指针的移动,可以快速定位目标值或满足特定条件的元素。
-
滑动窗口问题:滑动窗口问题通常涉及在数组或字符串上定义一个窗口,并通过移动窗口的左右边界来解决问题。左右指针可以用于表示窗口的左右边界,并根据问题的要求进行移动和调整。
-
两数之和、三数之和等问题:在有序数组中查找满足特定条件的数对或数组合时,左右指针可以进行逼近,快速找到满足条件的解。
-
回文字符串判断:左右指针可以用于判断字符串是否是回文字符串。通过左右指针从两端向中间移动,并比较对应位置的字符是否相等,可以判断字符串是否是回文。
1.3 快慢指针
快慢指针(Fast and Slow Pointers)基本思想是使用两个指针,一个指针(快指针 fast)移动速度较快,另一个指针(慢指针 slow)移动速度较慢。通过两个指针的相对移动,可以得到一些有用的信息,从而解决问题。
基本步骤
-
初始化快慢指针:将快指针和慢指针都指向链表的头节点或数组的起始位置。 s l o w = 0 , f a s t = 1 或 0 slow=0, fast=1 或 0 slow=0,fast=1或0
-
移动指针:根据问题的要求,通过移动快慢指针来逼近目标或获取有用的信息。
- 快指针移动:通常每次移动两步或一步,可以快速遍历整个链表或数组。 f a s t + = 1 fast +=1 fast+=1
- 慢指针移动:通常每次移动一步,慢指针的移动速度较慢。 s l o w + = 1 slow+=1 slow+=1
-
判断终止条件:根据问题的要求,判断是否满足终止条件。
- 例如,在链表中环检测问题中,如果快指针和慢指针相遇,则存在环;如果快指针到达链表末尾,则不存在环。
-
根据问题的要求返回结果。
- 例如,在链表中找到中间节点的问题中,当快指针到达链表末尾时,慢指针所指的节点就是中间节点。
伪代码模板
slow = 0
fast = 1
while 没有遍历完:if 满足要求的特殊条件:slow += 1fast += 1
return 合适的值
适用范围
-
链表中的环检测:快慢指针可以用于判断链表中是否存在环。快指针每次移动两步,慢指针每次移动一步,如果链表中存在环,则快指针最终会追上慢指针,二者相遇。
-
链表中点的查找:快慢指针可以用于找到链表的中间节点。快指针每次移动两步,慢指针每次移动一步,当快指针到达链表末尾时,慢指针正好在链表的中间位置。
-
链表倒数第k个节点的查找:快慢指针可以用于定位链表的倒数第k个节点。快指针先移动k个位置,然后快慢指针同时向前移动,当快指针到达链表末尾时,慢指针所指的节点就是倒数第k个节点。
-
判断链表是否有交点:快慢指针可以用于判断两个链表是否相交。分别使用快慢指针遍历两个链表,如果两个链表相交,则快指针和慢指针最终会相遇。
-
数组中的重复元素查找:快慢指针可以用于在数组中查找重复元素。通过快慢指针的移动,可以找到数组中的重复元素或判断数组是否存在重复元素。
1.4 分离双指针
分离双指针(Two Pointers with Separation)是一种双指针算法的变体,它通常用于解决数组或链表中需要分离的问题,例如将奇偶数分离、将0和非0元素分离等。分离双指针的基本思想是使用两个指针,一个指针(分离指针)用于分离元素,另一个指针(遍历指针)用于遍历数组或链表。通过移动遍历指针,并根据特定条件将元素交换到分离指针的位置,实现元素的分离。
基本步骤
-
两个指针 l e f t 1 left_1 left1、 l e f t 2 left_2 left2 。 l e f t 1 left_1 left1 指向第一个数组的第一个元素( l e f t 1 = 0 left_1=0 left1=0), l e f t 2 left_2 left2 指向第二个数组的第一个元素( l e f t 2 = 0 left_2=0 left2=0)。
-
当满足一定条件时
-
两个指针同时右移, l e f t 1 + = 1 、 l e f t 2 + = 1 left_1 += 1、left_2 += 1 left1+=1、left2+=1。
-
l e f t 1 left_1 left1 右移, l e f t 1 + = 1 left_1 += 1 left1+=1。
-
l e f t 2 left_2 left2 右移, l e f t 2 + = 1 left_2 += 1 left2+=1。
-
-
当其中一个数组遍历完时或者满足其他特殊条件时跳出循环体。
伪代码模板
left_1 = 0
left_2 = 0while left_1 < len(nums1) and left_2 < len(nums2):if 一定条件 1:left_1 += 1left_2 += 1elif 一定条件 2:left_1 += 1elif 一定条件 3:left_2 += 1
适用范围
分离双指针一般用于处理有序数组合并,求交集、并集问题
349. 两个数组的交集 - 力扣(LeetCode)

思路:分离双指针
- 两个数组先排序。( n u m s 1 、 n u m s 2 nums1、nums2 nums1、nums2)
- 使用两个指针分别指向两个数组的第一个元素,即第一个指针指向第一个数组的第一个元素,第二个指针指向第二个数组的第一个元素。( l e f t 1 = 0 、 l e f t 2 = 0 left_1=0、left_2=0 left1=0、left2=0)
- 如果 n u m s 1 [ l e f t 1 ] = = n u m s 2 [ l e f t 2 ] nums1[left_1]==nums2[left_2] nums1[left1]==nums2[left2] 则将其加入答案数组(注意去重),并将 l e f t 1 left_1 left1 和 l e f t 2 = 0 left_2=0 left2=0 右移 ( l e f t 1 + = 1 left_1 += 1 left1+=1 、 l e f t 2 + = 1 left_2 += 1 left2+=1)。
- 如果 n u m s 1 [ l e f t 1 ] < n u m s 2 [ l e f t 2 ] nums1[left_1] < nums2[left_2] nums1[left1]<nums2[left2] ,则 l e f t 1 left_1 left1 右移 。
- 如果 n u m s 1 [ l e f t 1 ] > n u m s 2 [ l e f t 2 ] nums1[left_1] > nums2[left_2] nums1[left1]>nums2[left2] ,则 l e f t 2 left_2 left2 右移 。
- 返回答案。
代码
class Solution:def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:nums1.sort()nums2.sort()left_1 = 0left_2 = 0res = []while left_1 < len(nums1) and left_2 < len(nums2):if nums1[left_1] == nums2[left_2]:if nums1[left_1] not in res:res.append(nums1[left_1])left_1 += 1left_2 += 1elif nums1[left_1] < nums2[left_2]:left_1 += 1elif nums1[left_1] > nums2[left_2]:left_2 += 1return res

2 滑动窗口基础知识
2.1 滑动窗口算法介绍
滑动窗口算法(Sliding Window Algorithm)是一种常用的算法技巧,用于解决数组或字符串相关的问题。它的基本思想是维护一个窗口,通过在数组或字符串上滑动窗口,不断更新窗口内的状态,从而解决问题。可以对窗口进行滑动操作、缩放操作,以及维护最优解操作。
- 滑动操作:窗口向一个方向移动,常见的是向右侧移动。
- 缩放操作:针对不固定长度的窗口,可以从左侧缩小窗口长度,也可以从右侧扩大窗口长度。
2.2 滑动窗口适用范围
滑动窗口算法通常适用于线性数据结构,如数组和字符串。它在处理大规模数据时特别有用,因为它可以通过滑动窗口的方式,仅对部分数据进行处理,而不需要遍历整个数据集。这使得滑动窗口算法具有较低的时间复杂度,并且在实际应用中常常能够提供高效的解决方案。
按照窗口长度的固定情况,我们可以将滑动窗口题目分为以下两种:
-
固定长度窗口:窗口大小是固定的。
-
不定长度窗口
-
窗口大小是不固定的。
-
求解最大的满足条件的窗口。
-
求解最小的满足条件的窗口。
-
2.3 固定长度滑动窗口
固定长度滑动窗口是一种特殊的滑动窗口算法,它的窗口大小固定,不会随着数据集的变化而变化。该算法通常用于需要对连续的数据序列进行处理的问题,如时间序列数据分析等。
固定长度滑动窗口的基本思想是:将数据序列分成若干个固定长度的子序列,然后对每个子序列进行处理。在处理每个子序列时,可以使用滑动窗口算法,通过移动窗口来更新子序列内的状态,从而得到最终的结果。
基本步骤
固定长度滑动窗口的步骤如下:
- 初始化窗口的起始位置和结束位置,窗口大小固定。
- 对于每个窗口内的子序列,根据问题要求更新窗口内的状态。
- 如果窗口满足特定条件,记录结果。
- 继续移动窗口的起始位置,重复上述步骤,直到遍历完整个数据集。
代码模板
left = 0
right = 0while right < len(nums):window.append(nums[right])# 超过窗口大小时,缩小窗口,维护窗口中始终为 window_size 的长度if right - left + 1 >= window_size:# ... 维护答案window.popleft()left += 1# 向右侧增大窗口right += 1
2.4 不固定长度滑动窗口
不定长度滑动窗口算法(Sliding Window):在给定数组 / 字符串上维护一个不定长度的窗口。可以对窗口进行滑动操作、缩放操作,以及维护最优解操作。
基本步骤
- 使用两个指针 l e f t left left、 r i g h t right right。初始时, l e f t left left、 r i g h t right right 都指向序列的第一个元素。即: l e f t = 0 left=0 left=0, r i g h t = 0 right=0 right=0,区间 [ l e f t , r i g h t ] [left,right] [left,right] 被称为一个「窗口」。
- 将区间最右侧元素添加入窗口中,即
window.add(s[right])。 - 然后向右移动 r i g h t right right,从而增大窗口长度,即
right += 1。直到窗口中的连续元素满足要求。 - 此时,停止增加窗口大小。转向不断将左侧元素移出窗口,即
window.popleft(s[left])。 - 然后向右移动 l e f t left left,从而缩小窗口长度,即
left += 1。直到窗口中的连续元素不再满足要求。 - 重复 2 ~ 5 步,直到 r i g h t right right 到达序列末尾。
代码模板
left = 0
right = 0while right < len(nums):window.append(nums[right])while 窗口需要缩小:# ... 可维护答案window.popleft()left += 1# 向右侧增大窗口right += 1
参考文献
- [1] https://datawhalechina.github.io/leetcode-notes/#/
—— END ——
如果以上内容有任何错误或者不准确的地方,欢迎在下面 👇 留言。或者你有更好的想法,欢迎一起交流学习~~~
更多精彩内容请前往 AXYZdong的博客
相关文章:

Leetcode算法入门与数组丨6. 数组双指针、滑动窗口
文章目录 1 双指针基础知识1.1 双指针简介1.2 左右指针(对撞指针)1.3 快慢指针1.4 分离双指针 2 滑动窗口基础知识2.1 滑动窗口算法介绍2.2 滑动窗口适用范围2.3 固定长度滑动窗口2.4 不固定长度滑动窗口 1 双指针基础知识 1.1 双指针简介 双指针&…...

推荐一本书《横向领导力》
大家好,这里是大话硬件。 今天想给大家推荐一本我近期正在阅读的书籍《横向领导力》。 这本书很早就买了,但是在去年就看了前面3章的内容,而且也没做笔记,仅仅是在书本上写写画画,也没有什么体会,感觉看不懂…...

React实战过程的知识了解
做项目用到react和antd,没办法循序渐进的学习,只能把一些点记录在这里,希望大家指正。 1.杂七杂八 正文 //actionRef,操作表单的预设方法,包括:刷新、重置所有项并刷新、重置到默认项、加载更多、清空选…...

F对象和Q对象
F对象和Q对象 F对象 一个F对象代表数据库中某条记录的字段的信息 作用: 通常是对数据库中的字段值在不获取的情况下进行操作 用于类属性(字段)之间的比较 语法 from django.db.models import F F(列名)解决一种极端事件的产生,比如用户对一条微博的点赞…...
Visio——绘制倾斜线段
一、形状 -> 图表和数学图形 -> 多行 二、放置多行线,可以发现存在两个折点 三、选择多行线,右键选择删除点,即可得到倾斜线段...
Linux复习-安装与熟悉环境(一)
这里写目录标题 虚拟机ubuntu系统配置镜像Linux命令vi编辑器3个模式光标命令vi模式切换命令vi拷贝与粘贴命令vi保存和退出命令vi的查找命令vi替换命令 末行模式复制、粘贴、剪切gcc编译器 虚拟机 VMware16 官网下载:vmware官网 网盘下载: 链接ÿ…...

Go基础语法:map
9 map Go 语言中提供的映射关系容器为 map ,其内部使用 散列表(hash) 实现。它是一种无序的基于 key-value 的数据结构。 Go 语言中的 map 是引用类型,必须初始化之后才能使用。 9.1 map 定义 Go 语言中 map 的定义语法为&…...
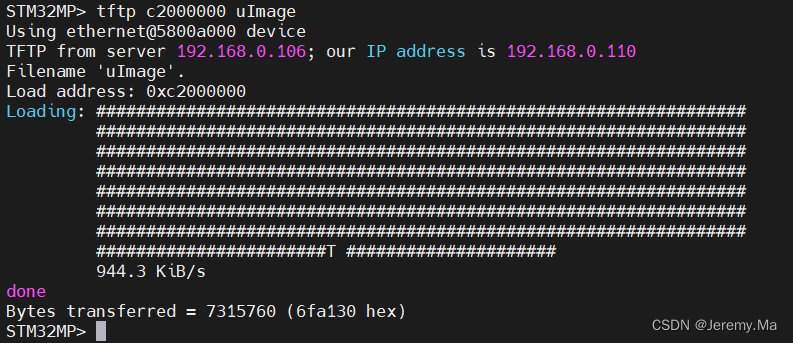
开发板TFTP调试
问题描述 开发板和host(此处指虚拟机linux)可以平通,但是通过uboot tftp下载请求时一直显示T T T, 即超时 使用wireshark抓包也显示超时 措施 关闭windows和linux的防火墙 重新进行下载成功...
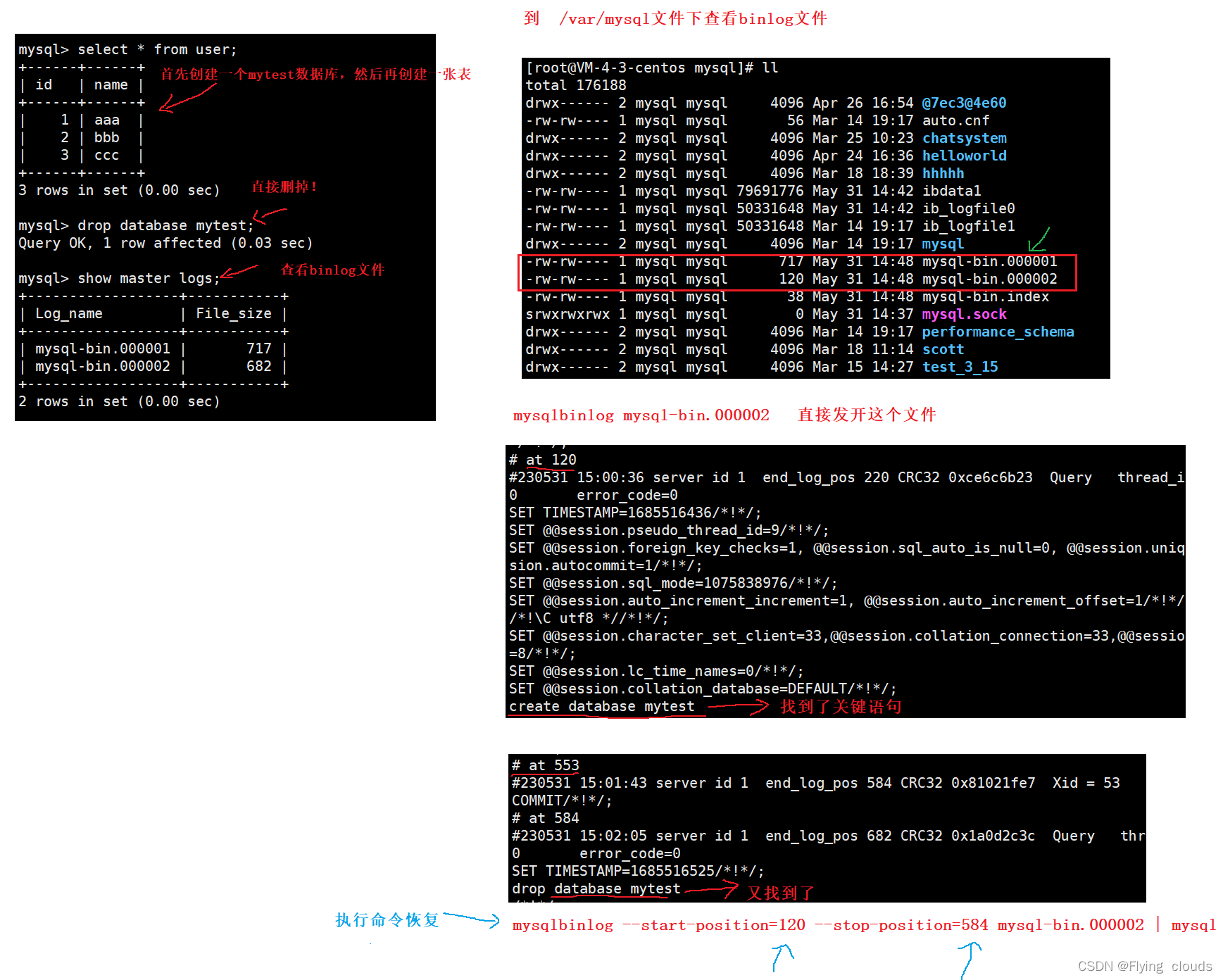
MySQL---优化日志
目录 一、MySQL优化 3、mysql server上的优化 3.1、MySQL查询缓存 3.2、索引和数据缓存 3.2、线程缓存 二、MySQL日志 2.1、redo log 重做日志 2.2、undo log 回滚日志 2.3、错误日志 2.4、查询日志 2.5、二进制日志 2.5.1、基于binlog数据恢复实践操作 六、慢查…...

【送面试题】深入解析Cookie和Session的请求区别及使用场景
AI绘画关于SD,MJ,GPT,SDXL百科全书 面试题分享点我直达 2023Python面试题 2023最新面试合集链接 2023大厂面试题PDF 面试题PDF版本 java、python面试题 项目实战:AI文本 OCR识别最佳实践 AI Gamma一键生成PPT工具直达链接 玩转cloud Studio 在线编码神器 玩转 GPU AI…...

010_第一代软件开发(二)
第一代软件开发(二) 文章目录 第一代软件开发(二)项目介绍界面布局功能完善快照功能获取可用串口播放按键提示音 关键字: Qt、 Qml、 QSerialPort、 QPixmap、 QSoundEffect 项目介绍 欢迎来到我们的 QML & C 项目!这个项目结合了 QMLÿ…...
)
基于若依ruoyi-nbcio增加flowable流程待办消息的提醒,并提供右上角的红字数字提醒(四)
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 上一节说到待办系统的监听器TaskCreateListener,需要在flowable全局监听配置里加入配置 1、Glo…...

RestTemplate:简化HTTP请求的强大工具
文章目录 什么是RestTemplateRestTemplate的作用代码示例 RestTemplate与HttpClient 什么是RestTemplate RestTemplate是一个在Java应用程序中发送RESTful HTTP请求的强大工具。本文将介绍RestTemplate的定义、作用以及与HttpClient的对比,以帮助读者更好地理解和使…...
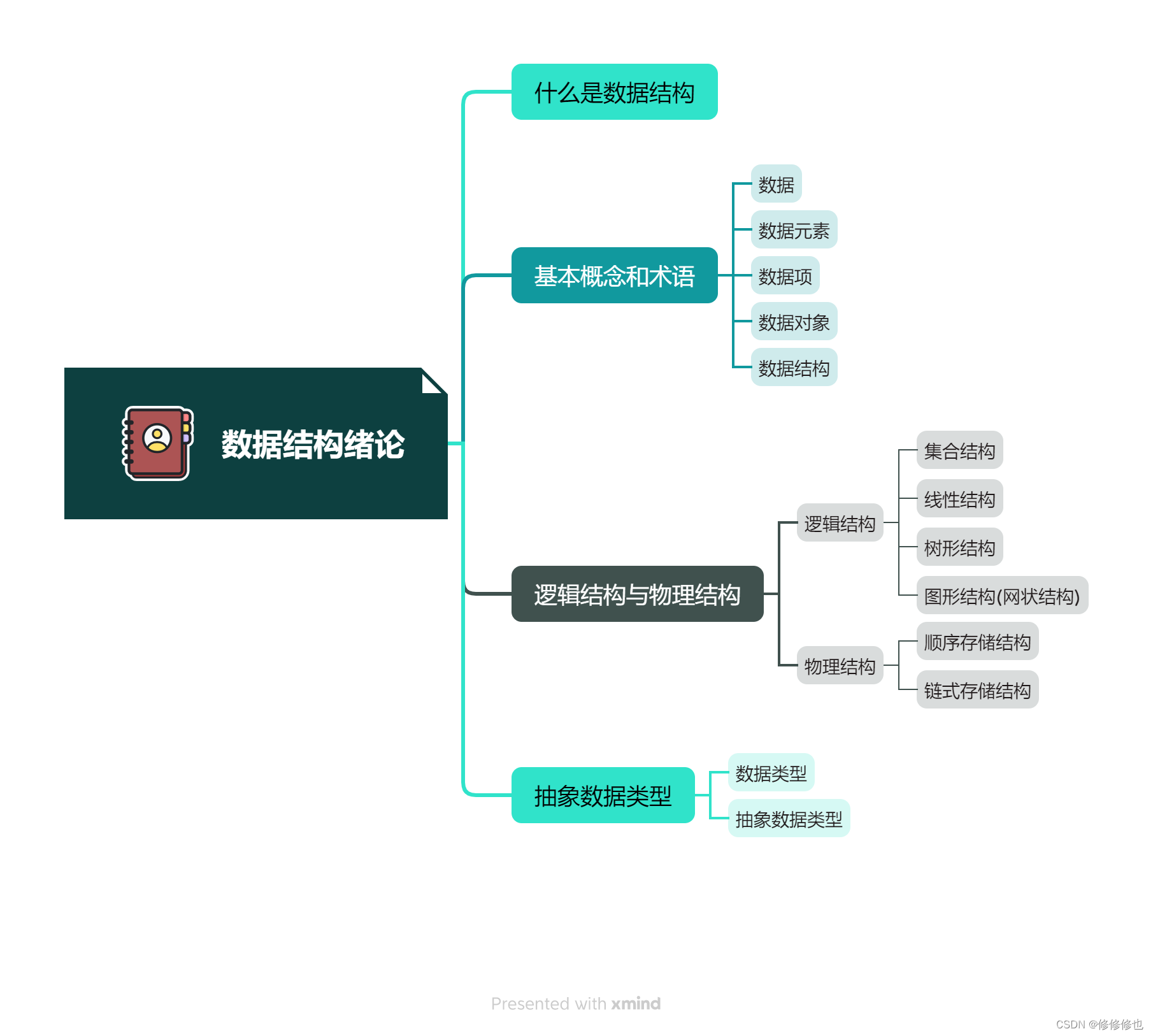
【数据结构】什么是数据结构?
数据结构(Data Structure)是计算机存储,组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合. 这么讲可能有些抽象,放一张图大家可能好理解一点: 上图依次是数据结构中逻辑结构中的:集合结构,线性结构,树形结构,图形结构. 而: 数据结构是一门研究非数值计算的程…...
的若干细节概要)
c++源码编译过程(翻译阶段)的若干细节概要
c程序的编译主要包含两个阶段:源码编译(翻译阶段)和目标文件链接。 源码编译过程主要有如下这些阶段: 阶段1: 翻译源码文本字符 阶段2: 逻辑源码行标准化处理 阶段3: 文法处理,分解为不同的源码文本类型序列。例如分解为注释、预处理指…...

Go内置函数make和new的区别?
首先纠正一下make 和 new 是内置函数,不是关键字。 变量初始化,一般分为2步,变量声明变量内存分配,var 关键字就是用来声明变量的,new和make 函数主要是用来分配内存的。 var 声明值类型的变量时,系统会默…...
动手学深度学习(pytorch版)第二章-2.3线性代数Note-linear-algebra
类型 标量:仅包含一个数值被称为标量 向量:向量可以被视为标量值组成的列表 矩阵:正如向量将标量从零阶推广到一阶,矩阵将向量从一阶推广到二阶。 A torch.arange(20).reshape(5, 4) A.T //转置 张量:是描述具有…...

Docker CMD指令如何覆写
在Dockerfile里,CMD指令是可以被覆盖的。 在构建镜像时,可以通过docker build命令的–cmd选项覆盖Dockerfile的CMD: 例如: FROM ubuntu CMD ["echo","hello"]构建时覆盖CMD: docker build -t test --cmd "echo world" .在创建容器时,可以通过…...

动手吧,vue单独使用的复选框
单独使用的复选框可以用在两个状态之间的切换,如是否阅读协议、记住账号等场景。 效果: 1、template部分 <template><label class"v-checkbox-single"><span class"v-checkbox_input" :class"{ disabled }&qu…...
升级iOS17后可以降级吗?iOS17退回iOS16方法教程分享
iOS 17已上线几天,从网上用户的反馈和媒体机构的报告来看,iOS17系统对旧机型来说并不友好,除了电池续航下降以外,占用大量储存空间,BUG也不少。 苹果于 9 月 7 日发布了 iOS 16.6.1 版本,如果升级iOS17后发…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
