数据结构:二叉树的基本概念
文章目录
- 1. 二叉树的定义
- 2. 二叉树的特点
- 3. 特殊二叉树
- 斜树
- 满二叉树
- 完全二叉树
- 4. 二叉树的性质
1. 二叉树的定义
如果我们猜一个100以内的数字,该怎么猜才能理论最快呢?
第一种方式:从1,2一直猜到100, 反正数字都是100以内,总能猜到的
第二种方式:先猜50,如果比结果小,猜75;如果比结果大,猜25.最后也能猜到对应的值
很显然,第二种方式明显优于第一种方式.第一种方式的时间复杂度是 O ( N ) O(N) O(N),而第二种方式的时间复杂度是 O ( l o g N ) O(logN) O(logN).
对于这种在某个阶段都是两种结果的情形,比如开和关,0和1,真和假等等,都适合用树状结构来建模,而这种树就是之前说的很优秀的树状结构,叫做二叉树.
二叉树(Binary Tree)是n(n>=0)个结点的有限集合.
- 该集合或者为空集(称为空二叉树).
- 或者由一个根节点和两棵互不相交,分别称为根节点的左子树和右子树的二叉树组成.
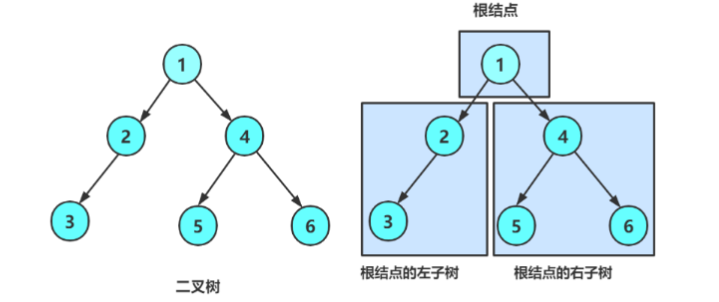
2. 二叉树的特点
根据上面的二叉树的图片,我们可以得到二叉树的以下特点
- 二叉树不存在度大于 2 的结点
二叉树每个结点最多度为2,即最多有左右两个子树,不存在或者只有一颗子树是可以的. - 二叉树的子树有左右之分,次序不能随意颠倒,因此二叉树是有序树
正如人的左脚和右脚不能随意颠倒,二叉树也分为左子树和右子树的;
即使某个结点只有一棵子树,也是要分清楚是左子树还是右子树的
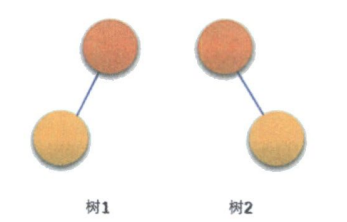
上图的两棵树虽然是同一棵树,但是不是同一棵二叉树
二叉树具有以下五种基本形态,任意的二叉树都是由下面的情况复合而成的
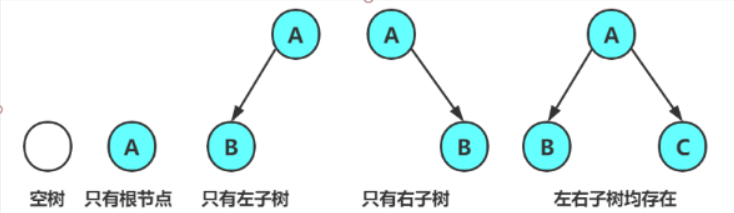
- 空二叉树
- 只有一个根结点
- 根节点只有左子树
- 根节点只有右子树
- 根节点既有左子树又有右子树
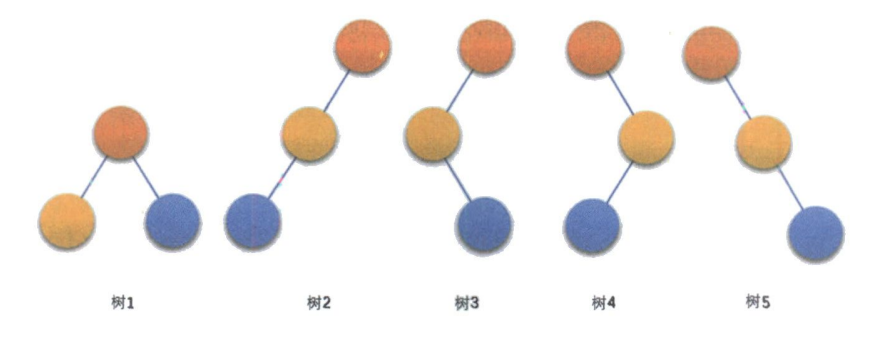
如果只从形态上考虑,三个结点的树只有两种情况,就是下图的树1和后面四个中的任意一种.
但是对于二叉树这个有序树而言,左右子树是由区别的,所以下面五种情况都表示不同的二叉树.
现实中的二叉树很漂亮,正如在数据结构中,二叉树这个树形结构也占据很重要的地位一样,有时候数学的美和大自然的美都是相通的.

3. 特殊二叉树
斜树
所有的结点都只有左子树的叫左斜树,所有的结点都只有右子树的叫右斜树.
这两者统称为斜树.
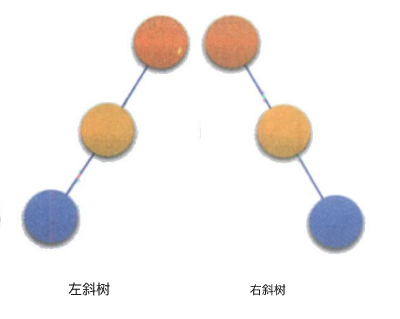
其实,线性表就是一种特殊的斜树,但是两者的逻辑结构还是不一样的,线性表是一对一线性结构的,而斜树是一对多树形结构的
满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有的叶子都在同一层上,这样的二叉树称为满二叉树
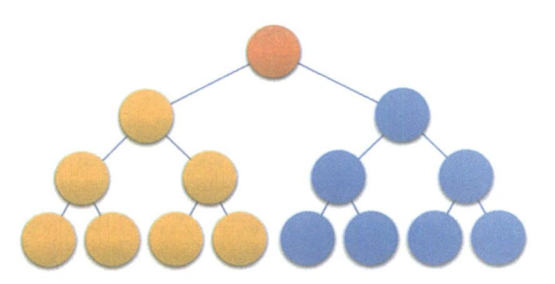
满二叉树有以下特点
- 叶子结点只能出现在最下一层
- 非叶子结点的度一定是 2
- 满二叉树的结点个数最多,叶子数最多.如果一个满二叉树有 K 层, 那么一共有 2 k − 1 2^k-1 2k−1个结点
完全二叉树
对一个具有 n 个节点的二叉树按层序编号, 如果编号为 i( 1 ⩽ i ⩽ n 1\leqslant i \leqslant n 1⩽i⩽n)的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中的位置完全相同, 则这颗二叉树称为完全二叉树.

最重要的是按层序编号
例如下面的三个二叉树,就不是完全二叉树.它们对应满二叉树的结点编号缺少了.
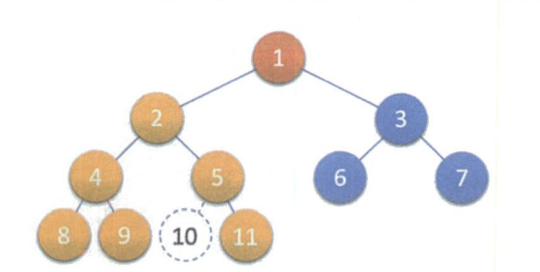
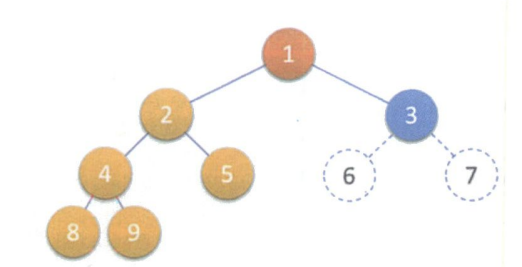
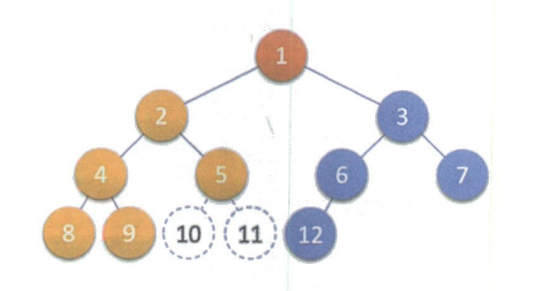
总而言之就是,除了最后一层的不满并且最后一层的从第一个结点开始是连续的,这就是完全二叉树.
完全二叉树有以下特点:
- 叶子结点只能出现在最下两层
- 最下层的叶子一定集中在左部连续位置
- 倒数两层,若有叶子结点,一定都在右部连续位置
- 如果结点度为1, 则该结点只有左孩子
- 同样节点数的二叉树,完全二叉树的深度最小
如果有h层, 那么完全二叉树的结点数为 [ 2 h − 1 , 2 h − 1 ] [2^{h-1}, 2^h - 1] [2h−1,2h−1]
4. 二叉树的性质
- 若规定根节点的层数为 1, 则一棵非空二叉树的第 i 层最多有 2 i − 1 2^{i-1} 2i−1个结点.
- 若规定根节点的层数为 1, 则深度为 h 的二叉树的最大结点数是 2 h − 1 2^h - 1 2h−1.
- 对任何一棵二叉树,如果度为 0 的叶子结点个数为 n 0 n_0 n0, 度为 2 的分支节点个数为 n 2 n_2 n2, 则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1.
- 若规定根节点的层数为 1 , 具有n个结点的满二叉树的深度, h = l o g 2 ( n + 1 ) log_2(n + 1) log2(n+1).
- 对于具有 n 个结点的完全二叉树, 如果按照从上至下, 从左至右的数组顺序对所有结点开始从 0 编号, 则对于序号为 i 的结点有:
- 若 i > 0, i位置结点的双亲序号: (i-1)/2; i=0, i为根节点编号, 无双亲结点.
- 若 2i+1<n, 左孩子序号: 2i+1, 2i+1 >=n 则无左孩子
i > 0, i位置结点的双亲序号: (i-1)/2**; i=0, i为根节点编号, 无双亲结点.- 若 2i+1<n, 左孩子序号: 2i+1, 2i+1 >=n 则无左孩子
- 若 2i+2<n, 右孩子序号: 2i+2, 2i+2 >=n 则无右孩子
相关文章:

数据结构:二叉树的基本概念
文章目录 1. 二叉树的定义2. 二叉树的特点3. 特殊二叉树斜树满二叉树完全二叉树 4. 二叉树的性质 1. 二叉树的定义 如果我们猜一个100以内的数字,该怎么猜才能理论最快呢? 第一种方式:从1,2一直猜到100, 反正数字都是100以内,总能猜到的 第二种方式:先猜50,如果比结果小,猜75…...

利用Socks5代理IP加强跨界电商爬虫的网络安全
随着跨界电商的兴起,爬虫技术在这个领域变得越来越重要。然而,网络安全一直是一个值得关注的问题。在本文中,我们将讨论如何利用代理IP和Socks5代理来增强跨界电商爬虫的网络安全,确保稳定和可靠的数据采集,同时避免封…...
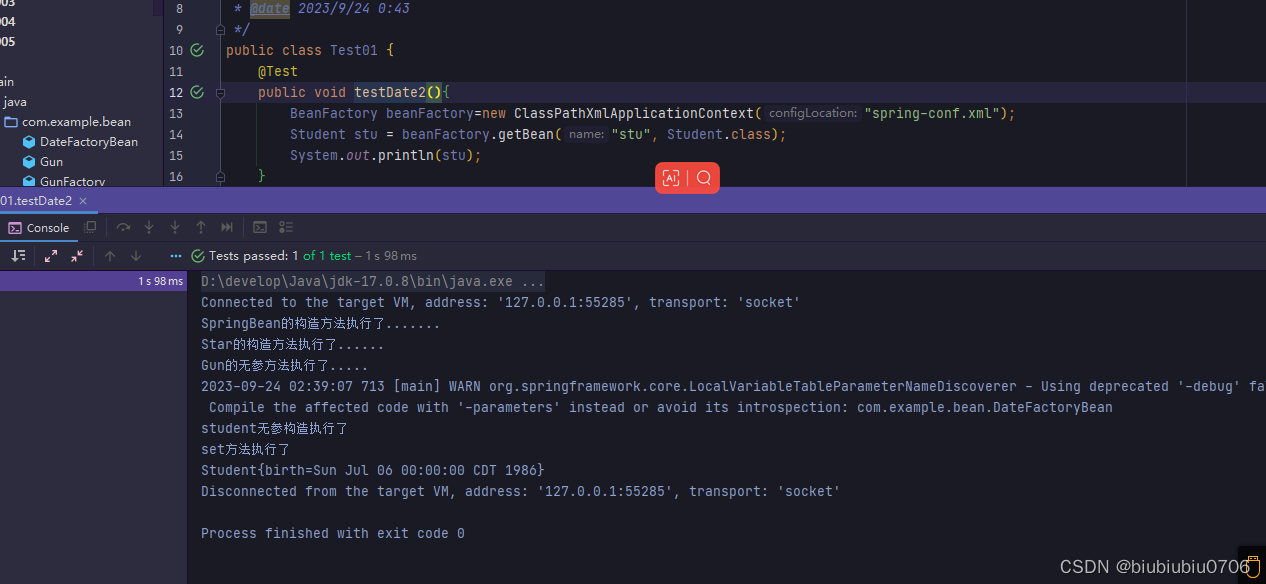
Spring学习笔记6 Bean的实例化方式
Spring学习笔记5 GoF之工厂模式_biubiubiu0706的博客-CSDN博客 Spring为Bean提供了多种实例化方式,通常包括4中(目的:更加灵活) 1.通过构造方法实例化 2.通过简单工厂模式实例化 3.通过factory-bean实例化 4.通过FactoryBean接口实例化 新建模块 spring-005 依赖 <!--S…...

大二毕设.3-网盘系统-用户模块讲解
目录 模块功能介绍 具体实现讲解 constants层:存放用户模块常量类 entity层:存放实体类,与数据库中的属性值基本保持一致 mapper层:对数据库进行数据持久化操作 service层:业务逻辑层,主要是针对具体…...

(Vue2)智慧商城项目
新增两个目录api、utils api接口模块:发送ajax请求的接口模块 utils工具模块:自己封装的一些工具方法模块 第三方组件库vant-ui PC端:element-ui(element-plus) ant-design-vue 移动端:vant-ui Mint UI…...

Nginx实战
虚拟主机 虚拟主机指的就是⼀个独⽴的站点,具有独⽴的域名,有完整的www服务,例如⽹站、FTP、邮件等 。Nginx⽀持多虚拟主机,在⼀台机器上可以运⾏完全独⽴的多个站点。⼀些草根流量站⻓,常会搭建个⼈站点进⾏资源分享交…...
动态规划 part 17)
day-57 代码随想录算法训练营(19)动态规划 part 17
647.回文子串 思路:动态规划 1.dp存储:判断以i开始,j结尾的字符串是否是回文串2.动态转移方程:当s[i]s[j]时,如果j-i<1,d[i][j]true; 如果 dp[i1][j-1]true,那么dp[i][j…...
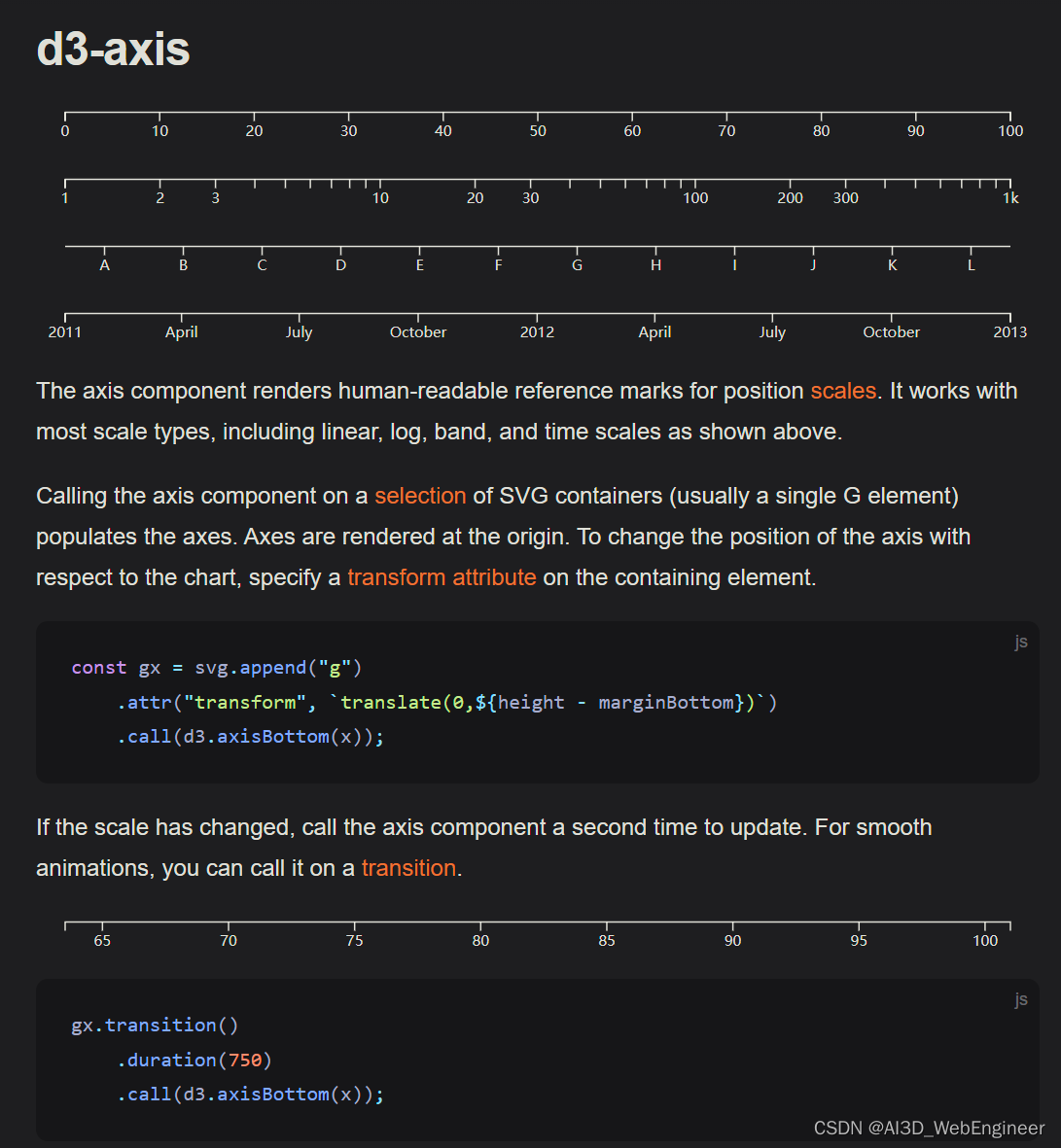
在项目中,关于前端实现数据可视化的技术选择
前言 在项目中,数据可视化以图表、报表类型为主。 需求背景 技术框架是Vue2.x版本,组件库是Ant Design of Vue能够支撑足够多的图表类型开发图表大小/位置能够随意变动图表样式需要支持丰富多样的用户配置强大、开放的图表语法支持复杂的数据可视化场景…...
DT 卡通材质学习 一
渐变着色器 相交线 笔刷和卡通结合使用 修改器...

【游戏引擎架构】6.2 资源管理器
资源管理器可以分为离线部分系统和运行时系统 文章目录 离线资源管理数据库资产管道 运行时资源管理文件结构内存管理文件间引用 离线资源管理 数据库 UE的数据库可以直接浏览、编辑资产,看到运行时的状态;但也存在两个较大的缺点: 版本管…...
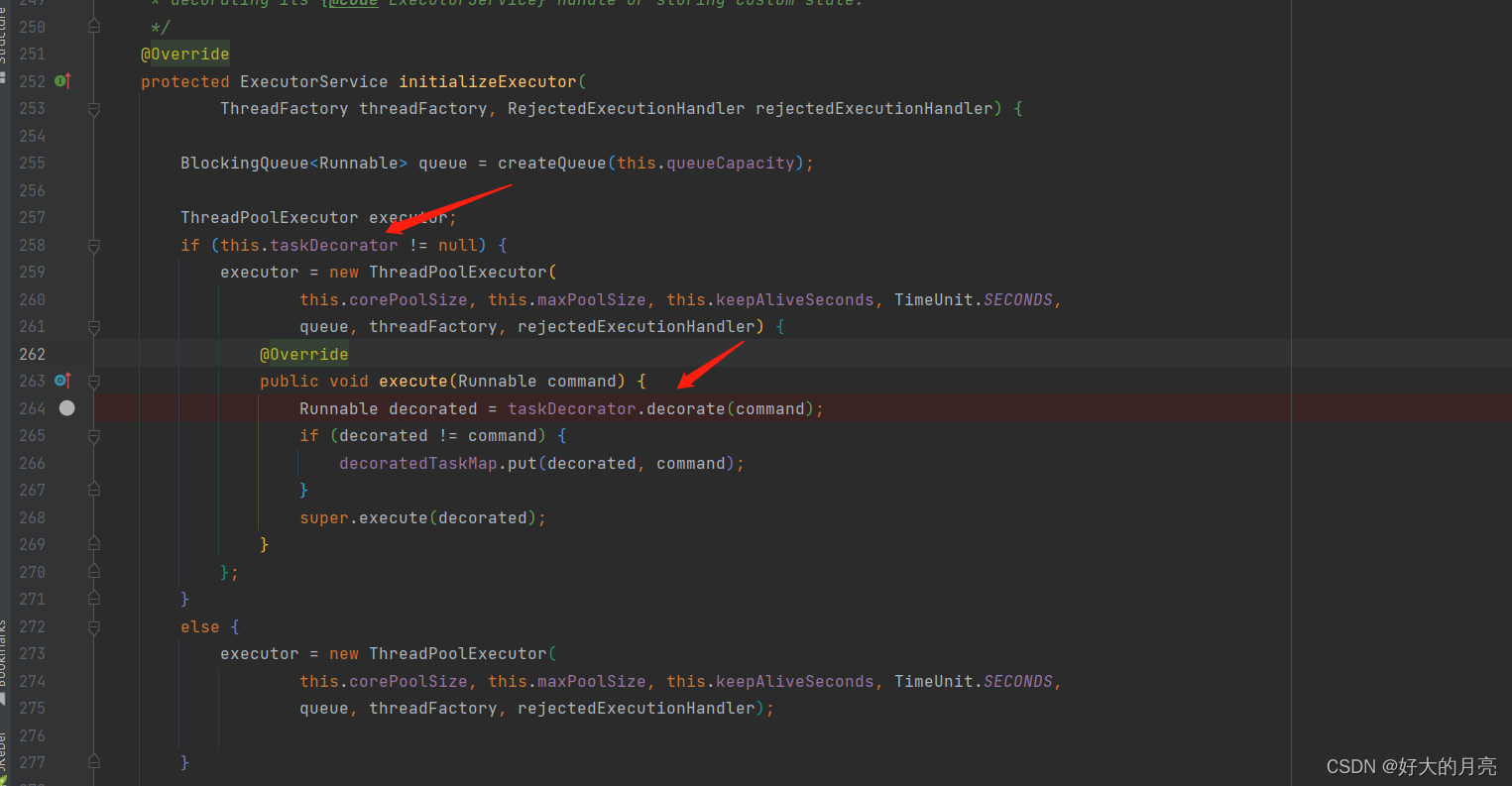
spring的ThreadPoolTaskExecutor装饰器传递调用线程信息给线程池中的线程
概述 需求是想在线程池执行任务的时候,在开始前将调用线程的信息传到子线程中,在子线程完成后,再清除传入的数据。 下面使用了spring的ThreadPoolTaskExecutor来实现这个需求. ThreadPoolTaskExecutor 在jdk中使用的是ThreadPoolExecutor…...

转载 - 洞察问题本质,解决工作难题
作者:关苏哲 高效管理者的三大技能 问题界定的6个问题 1.你所需要解决的问题是什么? 2.你为什么需要解决这个问题? 3.你期待的理想结果是什么? 4.这个问题包括哪些子问题? 5.你曾经尝试过哪些解决方式?…...
关于计算机找不到d3dx9_43.dll,无法继续执行代码修复方法
d3dx9_43.dll是一个动态链接库文件,它是DirectX的一个组件,主要用于处理游戏中的图形、声音等多媒体元素。当这个文件丢失时,可能会导致以下问题: 1. 游戏无法正常运行:由于d3dx9_43.dll负责处理游戏中的多媒体元素&a…...

《从零开始的Java世界》01基本程序设计
《从零开始的Java世界》系列主要讲解Javase部分,从最简单的程序设计到面向对象编程,再到异常处理、常用API的使用,最后到注解、反射,涵盖Java基础所需的所有知识点。学习者应该从学会如何使用,到知道其实现原理全方位式…...
【数据开发】数据全栈知识架构,数据(平台、开发、管理、分析)
文章目录 一、数据全栈知识架构1、数据方法(思维,统计学,实践,北极星)2、数据工具:数据仓库3、数据规范 二、数据分析工具1、大数据平台2、数据开发:入库计算(重点)3、数…...
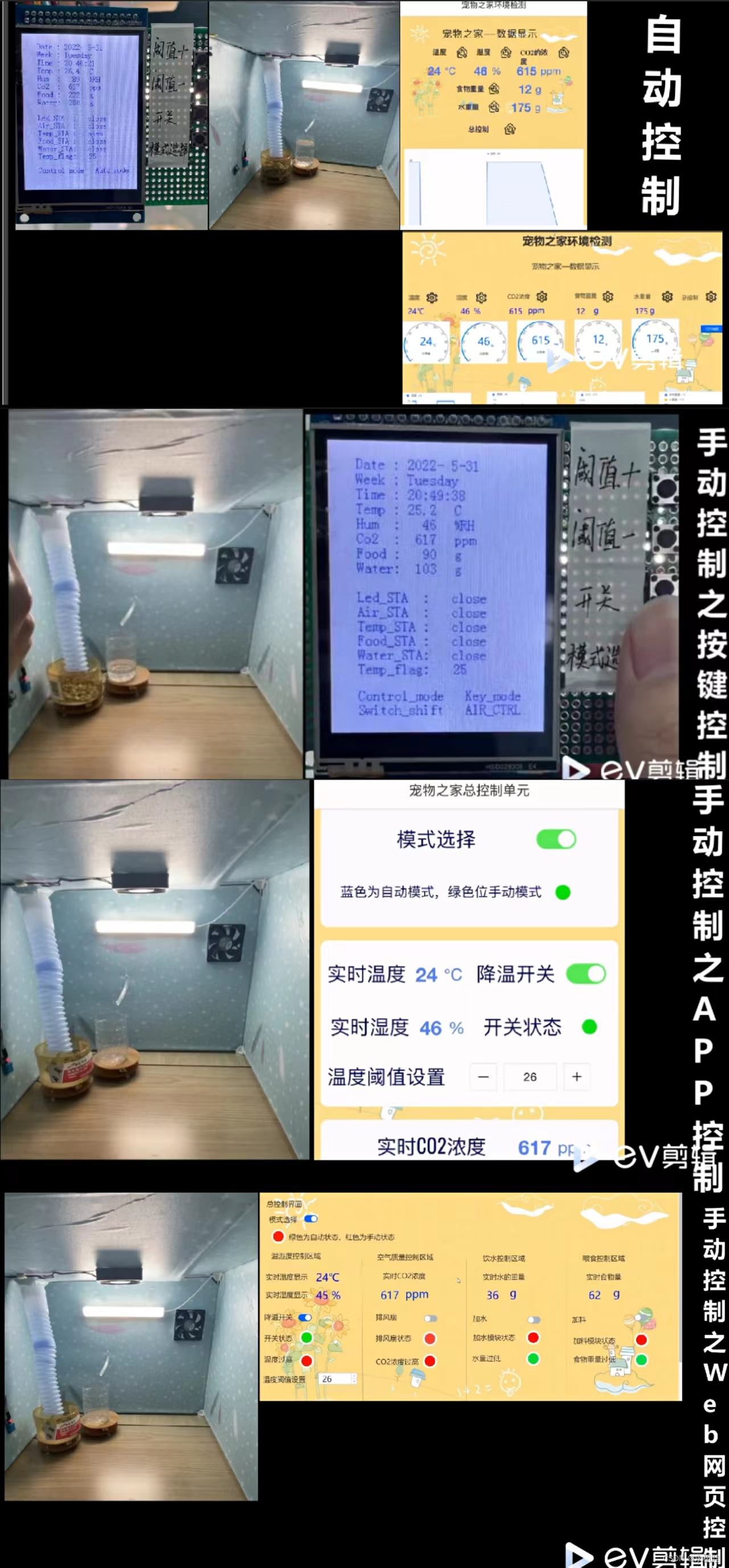
基于STM32的宠物托运智能控制系统的设计(第十七届研电赛)
一、功能介绍 使用STM32作为主控设备,通过DHT11温湿度传感器、多合一空气质量检测传感器以及压力传感器对宠物的托运环境中的温湿度、二氧化碳浓度和食物与水的重量进行采集,将采集到的信息在本地LCD显示屏上显示,同时,使用4G模块…...

数据结构的奇妙世界:实用算法与实际应用
文章目录 数据结构和算法的基本概念数据结构数组链表栈队列树图 算法 常见的数据结构和算法排序算法快速排序示例 数据结构的应用数据库管理系统图像处理网络路由 数据结构和算法的性能分析时间复杂度空间复杂度 如何更好地编写代码避免常见错误结论 🎉欢迎来到数据…...

uniapp实现表格冻结
效果图如下: 思路: 1.由于APP项目需要,起初想去插件市场直接找现成的,结果找了很久没找到合适的(有的不支持vue2有的不能都支持APP和小程序) 2.后来,就只能去改uni-table源码了,因…...

Spring面试题11:什么是Spring的依赖注入
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:说一说Spring的依赖注入 依赖注入(Dependency Injection)是Spring框架的一个核心特性,它是指通过外部容器将对象的依赖关系注入到对象中,从而…...
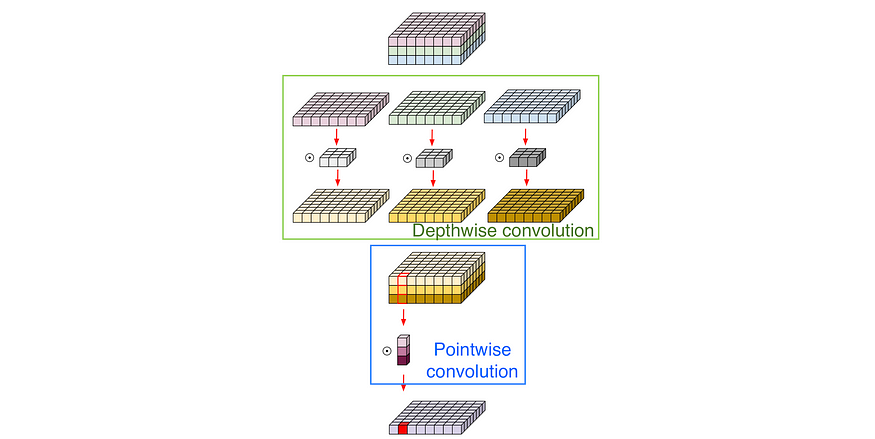
用于设计 CNN 的 7 种不同卷积
一 说明 最近对CNN架构的研究包括许多不同的卷积变体,这让我在阅读这些论文时感到困惑。我认为通过一些更流行的卷积变体的精确定义,效果和用例(在计算机视觉和深度学习中)是值得的。这些变体旨在保存参数计数、增强推理并利用目标…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
