《计算机视觉中的多视图几何》笔记(10)
10 3D Reconstruction of Cameras and Structure
本章主要描述了如何利用2张图片来恢复相机的参数以及物体在三维空间中的形状。
文章目录
- 10 3D Reconstruction of Cameras and Structure
- 10.1 Outline of reconstruction method
- 10.2 Reconstruction ambiguity
- 10.3 The projective reconstruction theorem
- 10.4 Stratified reconstruction
- 10.4.1 The step to affine reconstruction
- Translational motion
- Scene constraints
- The infinite homography
- One of the cameras is affine
- 10.4.2 The step to metric reconstruction
- 10.4.3 Direct metric reconstruction using ω \omega ω
- 10.5 Direct reconstruction – using ground truth
本章其实要解决两个问题。如何以及在多大程度上可以从两个视图中恢复场景和摄像机的空间布局。
- 三维空间的点 X i X_i Xi,是未知量。已知量是: x i x_i xi位于第一幅图像而 x i ′ x'_{i} xi′位于第二幅图像。而且已知 x i x_i xi与 x i ′ x'_i xi′是相互对应的: x i ↔ x i ′ x_i \leftrightarrow x'_i xi↔xi′,它们都是3D点 X i X_i Xi分别在第一、第二幅图像上的投影点,用公式表示为: x i = P X i x_i = PX_i xi=PXi, x i ′ = P ′ X i x'_i = P'X_i xi′=P′Xi。如果点太少,这项任务是不可能完成的。然而,如果存在足够多的点对应关系以允许唯一地计算基本矩阵 F F F,则可以将场景重建。
- 三维重建就是要找到 P , P ′ P, P^{'} P,P′,重建是有歧义的,歧义具体是指什么,如何消除这种歧义。如果提供有关摄像机或场景的附加信息,可以减少重建中的模糊性。 我们描述了一种两阶段的方法,其中歧义首先减少为仿射,然后减少为度量; 每个阶段都需要相应类别的信息。
10.1 Outline of reconstruction method
从2张图片来进行重建,步骤如下:
- 根据 x i ↔ x i ′ x_i \leftrightarrow x'_i xi↔xi′计算基本矩阵 F F F,其具体过程在11章叙述
- 根据 F F F求出摄像机外参 R , T R,T R,T,具体过程参见结论9.14
- 根据 R , T R,T R,T, x i ↔ x i ′ x_i \leftrightarrow x'_i xi↔xi′求解 X i X_i Xi,这个过程叫三角化,具体步骤在12章
该方法可以有多种变体。 例如,如果相机被校准,那么我们将计算基本矩阵而不是基本矩阵。 此外,可以使用有关相机运动、场景约束或部分相机校准的信息来获得重建的细化。
要点:三角化唯一不能确定的点就是基线上的点,因为从两个光心出发的射线互相重合了。在这种情况下,反投影光线共线(均等于基线)并沿其整个长度相交。

10.2 Reconstruction ambiguity
如果我们仅仅知道若干图像,不可能恢复出三维空间点的绝对位置。
原因如下:
我们定义相似变换 H S H_{S} HS
[ R t 0 T λ ] \left[ \begin{matrix} R & t \\ 0^T & \lambda \\ \end{matrix} \right] [R0Ttλ]
我们有
P X i = ( P H s − 1 ) ( H s X i ) PX_i = (PH^{-1}_s) (H_sX_i) PXi=(PHs−1)(HsXi)
如果把 P P P分解为 P = K [ R P ∣ t P ] P=K[R_{P}|t_{P}] P=K[RP∣tP],那么
P H S − 1 = K [ R P R − 1 ∣ t ′ ] PH^{-1}_{S}=K[R_{P}R^{-1}|t'] PHS−1=K[RPR−1∣t′]
该结果表明乘 H S − 1 H_{S}^{-1} HS−1不会改变 P P P的校准矩阵。因此,即使对于校准过的相机,重建也存在模糊性。对于校准相机来说,这是重建的唯一模糊之处。 因此,对于校准相机,可以通过相似变换进行重建。
因为 λ \lambda λ是任意的,所以有很多的 H s H_s Hs可以满足前式。几何解释如P265图10.2。

如果摄像机的内参也不知道,那么 H H H矩阵就是投影变换,投影变换只能保持直线还是直线,但是直线之间的角度就无法保持了。
以下介绍几种不同的重建类型。
10.3 The projective reconstruction theorem
Projective reconstruction的特点是相机没有标定。
结论 10.1:如果两幅图像中若干对应点已知,具体表示为 x i ↔ x i ′ x_i \leftrightarrow x^{'}_i xi↔xi′,那么我们可以求出基本矩阵 F F F,只需要 F F F就可以重建出三维空间中的点。而且任意更换相机投影矩阵,对重建没有影响,因为不同重建之间是等价的(比如第一次重建用的是 P 1 , P 1 ′ P_1,P'_1 P1,P1′,第二次重建用的是 P 2 , P 2 ′ P_2,P'_2 P2,P2′,但是点不能换,不管第一次重建还是第二次重建,都是用 x i ↔ x i ′ x_i \leftrightarrow x^{'}_i xi↔xi′,具体见书P266。
10.4 Stratified reconstruction
Stratified reconstruction指的是先有一个projective reconstruction,然后再把它优化到affine reconstruction最终metric reconstruction,如果可以的话。当然,需要注意的是想要得到affine或者metric reconstruction都需要额外知道一些关于重建场景本身的信息,或者相机要被标定过。
10.4.1 The step to affine reconstruction
我们现有一个project reconstruction的结果,记为 ( P , P ′ , { X i } ) (P,P^{'},\{X_i\}) (P,P′,{Xi})。 现在我们需要找出一个平面 π \pi π,使其成为无穷远平面 ( 0 , 0 , 0 , 1 ) (0,0,0,1) (0,0,0,1)在图像上的投影。则必然存在一个 H H H,满足 H − 1 π = ( 0 , 0 , 0 , 1 ) H^{-1}\pi = (0,0,0,1) H−1π=(0,0,0,1), H H H可以写成如下形式:
[ I ∣ 0 π T ] \left[ \begin{matrix} I | 0 \\ \pi^T \\ \end{matrix} \right] [I∣0πT]
找到了 H H H以后,把 H H H作用在所有重建得到的点上就完成了affine reconstruction。affine的意思就是说把我们得到的某平面投影到无穷远处。
那么如何找出 ( 0 , 0 , 0 , 1 ) (0,0,0,1) (0,0,0,1)到底映射到已知图像上的什么地方?以下给出几个例子。
Translational motion
简单来说就是摄像机从不同位置拍两幅图,但是摄像机本身只能有平移,不能有旋转。那么这两幅图中有一些点是没有移动的,比如月亮,比如一条延伸到无穷远处的公路。这样的话,月亮这一点的三维坐标写成 X i X_i Xi, 在两幅图像中的坐标写成 x i , x i ′ x_i,x^{'}_i xi,xi′。这样三个点就确定了一个平面。该平面就是 ( 0 , 0 , 0 , 1 ) (0,0,0,1) (0,0,0,1)投影到拍摄图像上的结果。这两图拍摄图像对应的基本矩阵 F F F是一个斜对称(skew-symmetric)矩阵。
Scene constraints
场景约束主要目的就是为了找三个在无穷远平面上的点。比方说两个平行线为一组,可以确定无穷远平面上的一个点,这样找三组就可以了。具体步骤参见12章,13章。
另外一个需要注意的是,在一副图像中找出无穷远点以后,可以利用基本矩阵找出第二幅图像中的对应点,不用重新算一遍。
第二种方法是用相交直线之间的比例关系,具体过程参见书P47。
The infinite homography
当我们找出了无穷远平面 ( 0 , 0 , 0 , 1 ) (0,0,0,1) (0,0,0,1)在图像中的投影,我们实质上确定了一个映射 H ∞ H_{\infty} H∞, H ∞ H_{\infty} H∞把图像 P P P中的点映射到 P ′ P' P′。具体可以表示为 x ′ = H ∞ x i x' = H_{\infty}x_i x′=H∞xi。
怎样求出这个 H ∞ H_{\infty} H∞? 假设我们现在有一个affine reconstruction,两个摄像机的外参表示为 P = [ M ∣ m ] P=[M|m] P=[M∣m], P ′ = [ M ′ ∣ m ′ ] P'=[M'|m'] P′=[M′∣m′], H ∞ = M ′ M − 1 H_{\infty} = M'M^{-1} H∞=M′M−1
H ∞ H_{\infty} H∞还可以通过基本矩阵 F F F和三对无穷远点来计算,参见13章
One of the cameras is affine
在这种情况下如何求出affine reconstruction。我们有以下结论:
结论 10.4 ( P , P ′ , { X i } ) (P,P',\{X_i\}) (P,P′,{Xi}) 是一个projective reconstruction。 P = [ I ∣ 0 ] P=[I|0] P=[I∣0]。所以 P P P是一个affine摄像机,那么affine reconstruction可以这样获得:交换 P , P ′ P,P' P,P′的最后两列,交换 { X i } \{X_i\} {Xi}的最后两个坐标。
10.4.2 The step to metric reconstruction
metric reconstruction的要点是找到absolute conic。
比较实际的做法是在图像中找到absolute conic,该conic反投影回无穷远处的平面,就变成了cone,那么这个cone就定义了无穷远处的absolute conic。
结论 10.5 假设图像中的absolute conic已知,记为 ω \omega ω,affine reconstruction的相机外参已知,记为 P = [ M ∣ m ] P=[M|m] P=[M∣m],那么affine reconstruction就可以利用一个矩阵 H H H变成metric reconstruction。 H H H如下所示:
[ A − 1 0 0 1 ] \left[ \begin{matrix} A^{-1} & 0 \\ 0 & 1 \\ \end{matrix} \right] [A−1001]
其中 A A A 满足 A A − 1 = ( M T ω M ) − 1 AA^{-1} = (M^{T}\omega M)^{-1} AA−1=(MTωM)−1
我们可以把上式右边用Cholesky factorization处理,就可以得到 A A A。
那么接下来的问题就是如何找到图像中的absolute conic?我们用 ω \omega ω来表示该conic。我们可以对该conic施加一些约束,然后再求解它。有这么几个约束:
-
被重建场景中的正交性
消失点 v 1 , v 2 v_1,v_2 v1,v2分别来自两个正交的直线,那么他们满足 v 1 T ω v 2 = 0 v_1^{T} \omega v_2 = 0 v1Tωv2=0确定一个conic需要五个参数,那么找三对 v 1 , v 2 v_1,v_2 v1,v2就可以解出这个方程。或者 v 1 , v 2 v_1,v_2 v1,v2分别来自一条直线和一个平面(直线与平面正交)。 则他们满足 l = ω v l=\omega v l=ωv。 -
相机内参
因为 ω = K − T K − 1 \omega = K^{-T}K^{-1} ω=K−TK−1 -
根据上一条约束,我们知道 ω \omega ω只和相机内参有关系,跟外参没关系。那么我们可以用同一个相机在两个不同位置拍摄。这个过程可以表示为 ω ′ = H ∞ − T ω H ∞ − 1 \omega^{'} = H^{-T}_{\infty} \omega H^{-1}_{\infty} ω′=H∞−TωH∞−1。 找出足够多的 H ∞ H_{\infty} H∞ 也可以解出这个方程。
10.4.3 Direct metric reconstruction using ω \omega ω
我们有一个projective reconstruction,我们还知道 ω \omega ω,把 ω \omega ω在无穷远平面上的位置记为 Ω ∞ \Omega_{\infty} Ω∞,然后 ω \omega ω所在的平面记为 π ∞ \pi_{\infty} π∞。那么从 ω \omega ω到 Ω ∞ \Omega_{\infty} Ω∞的矩阵就可以求解出来,参见书P342练习题(x),知道这个矩阵,把它作用在projective的重建结果上,就得到了metric重建的结果。
10.5 Direct reconstruction – using ground truth
假设我们知道一些三维点的gt,记为 X E i X_{Ei} XEi,重建出来的点记为 X i X_i Xi,那么他们满足 X E i = H X i X_{Ei} = HX_i XEi=HXi,因为前文说过重建时有歧义的。我们把 X i X_i Xi替换为图像中的点 x i x_i xi那么就有 x i = P H − 1 X E i x_i = PH^{-1}X_{Ei} xi=PH−1XEi。找出足够多的点,解这个方程就可以了。当我们知道了 H H H,就可以 H H H乘到相机矩阵 P , P ′ P,P^{'} P,P′上,这样projective重建就变成了真实的三维坐标。
相关文章:

《计算机视觉中的多视图几何》笔记(10)
10 3D Reconstruction of Cameras and Structure 本章主要描述了如何利用2张图片来恢复相机的参数以及物体在三维空间中的形状。 文章目录 10 3D Reconstruction of Cameras and Structure10.1 Outline of reconstruction method10.2 Reconstruction ambiguity10.3 The proje…...
【一、虚拟机vmware安装】
安装虚拟机 下载 官方下载地址:https://www.vmware.com/cn.html 大概流程就是,最重要的事最后一步...
uniapp 离线打包 plus.runtime.install 安装页面不弹起
uniapp 离线打包 plus.runtime.install 安装页面不弹起 updateVersion(webview : any, eventTitle : string, eventContent : string) {const loading plus.nativeUI.showWaiting(准备下载);var dtask plus.downloader.createDownload(eventContent,{method: GET,timeout: 5…...

Docker 自动化部署(保姆级教程)
Docker 自动化部署 1. jenkins 介绍1.1 参考链接:1.2 jenkins 概述1.3 jenkins部署项目的流程 2. jenkins 安装2.1 基于docker 镜像2.2 启动 jenkins 后端服务2.3 登录 jenkins 服务后端 3. jenkins自动化部署开始3.1 下载需要的插件3.2 创建任务3.2.1 描述3.2.2 配…...
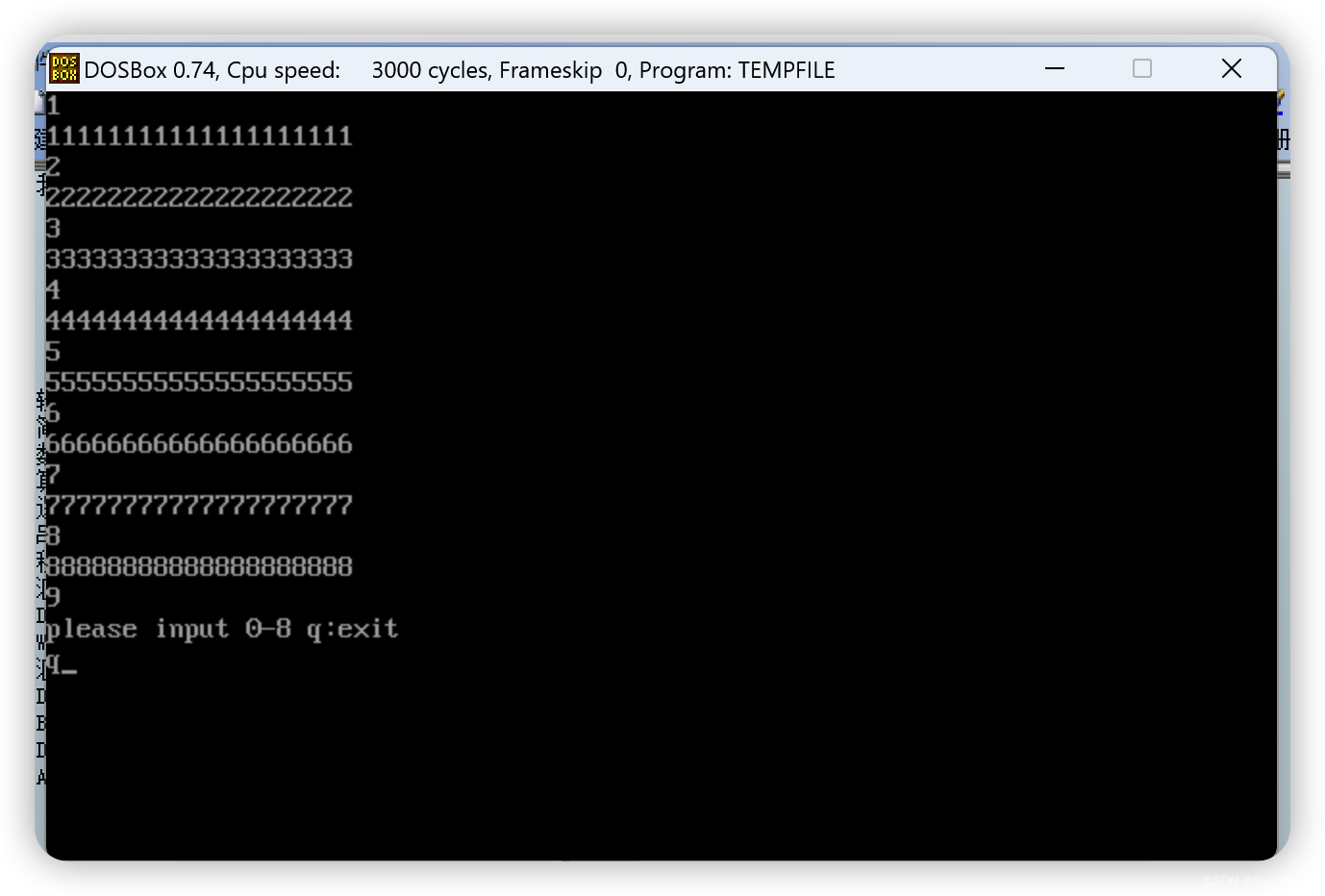
北工大汇编题——分支程序设计
题目要求 信息检素程序设计:在数据区,有9个不同的信息,编号 0-8,每个信息包括20 个字符。从键盘接收 0-8 之间的一个编号,然后再屏幕上显示出相应编号的信息内容,按“q”键退出 完整代码 DATAS SEGMENTn0…...
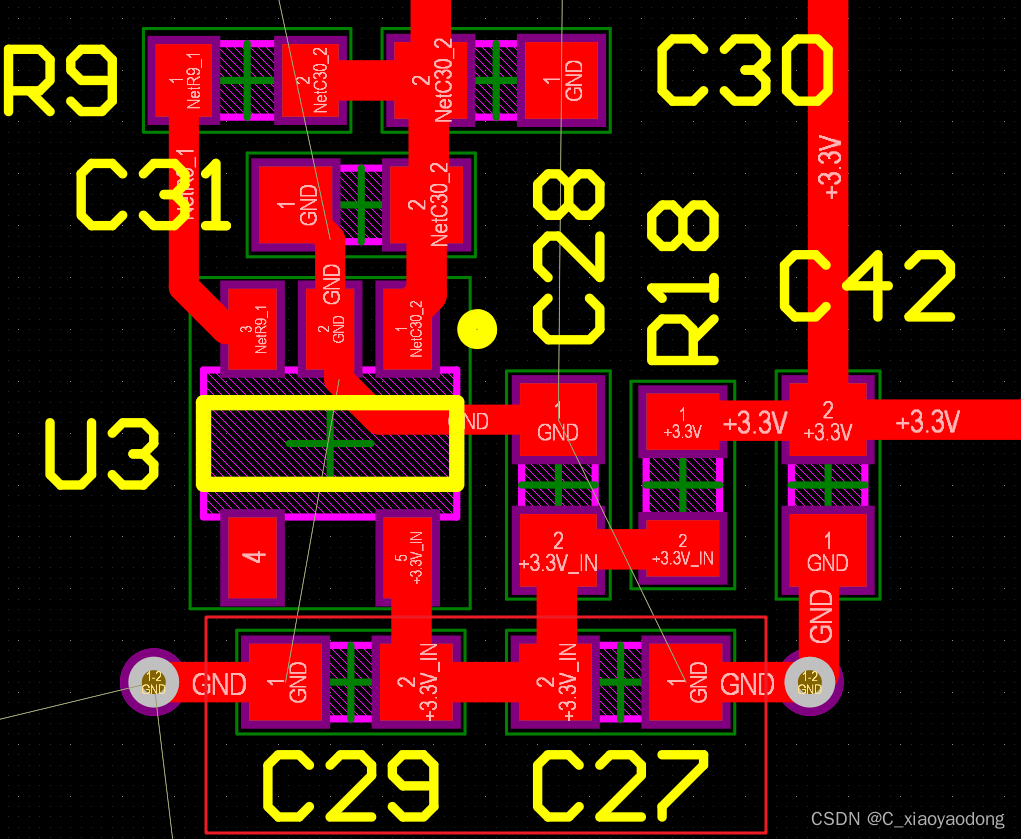
贴片电容耐压值选取和特性(包含实际电路和PCB)
一、一般电容的特性 ①容值大的电容,一般通低频率; ②容值小的电容,一般通高频率。 注:详细请看这位博主的篇文章: 大电容为什么虑低频小电容为什么又虑高频?(个人整理) 二、贴片电容的耐压选取 ①贴片电容有2…...
)
【云原生】kubernetes中pod(进阶)
目录 一、资源限制 业务cpu 内存 1.1CPU 资源单位 1.2 内存 资源单位 示例1 示例2: 二、健康检查:又称为探针(Probe) 2.1探针的三种规则 2.2 Probe支持三种检查方法 2.3示例 示例1:exec方式 示例3…...

Cesium 问题:获取高度值,高度值又是相对于谁来说的
文章目录 问题分析 问题 今天在开发中,甲方提出一个这样的问题,你的高度是怎么算出来的,对此,我只知道使用并不知道怎么来的,因此特意查了一番资料,希望帮助到大家 分析 在 Cesium 中,我们可以使…...
第三、四、五场面试
第三场 共享屏幕做题(三道简单题) 替换空格成%20(双指针) 删除升序链表中的重复元素(指针)有效的括号(栈) 第四场、第五场 自我介绍 项目拷打 整个项目架构rpc模块的情况分析的数…...
力扣-290.单词规律
Idea 先建立一个hashmap,记录s串中的每个单词以及对应的下标再建立一个hashmap,记录pattern串中相同字母以及对应的下标遍历pattern串时,遇到不同字母存到pat表中,同时将下标对应的s中的单词存入到查重test集中,因为如…...

常见限流算法学习
文章目录 常见限流算法学习前言限流算法基本介绍固定窗口计数器限流算法计数器限流算法相关介绍计数器限流算法的实现(基于共享变量)计数器限流算法的实现(基于Redis) 滑动窗口计数器算法滑动时间窗口算法相关介绍介绍滑动时间窗口…...

JS面试相关
深拷贝、浅拷贝、递归、优化 扁平化 柯里化 this指向原型 继承 call、apply、bind js取整的方法,parseInt第二个参数是什么 forEach和map有什么区别,使用场景? 内存泄漏的场景 原型链原型 严格模式 Js中for in 和for of的区别 slice、splice、…...
SSRF漏洞
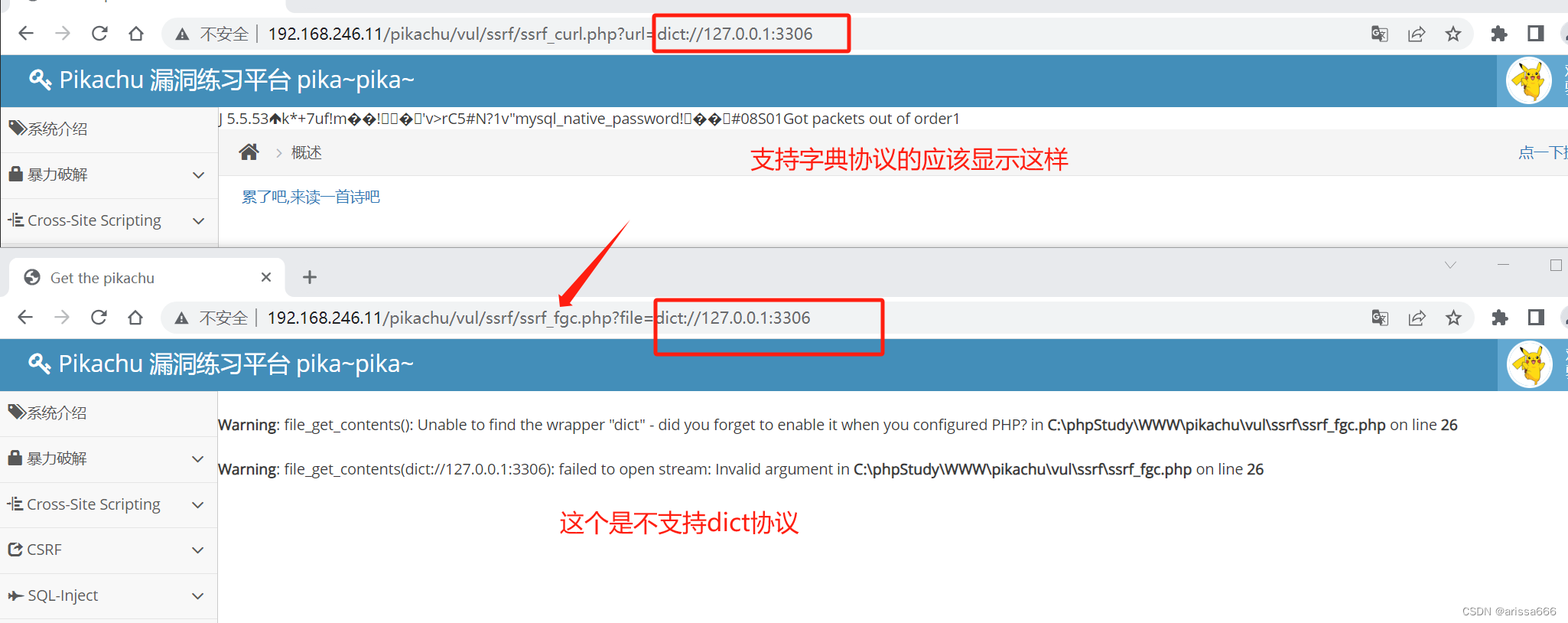
Server-Side Request Forgery:服务器端请求伪造 目标:网站的内部系统 形成的原因 攻击者构造形成由服务器端发起请求的译者安全漏洞。 由于服务端提供了从其他服务器应用获取数据的功能,且没有对目标地址做过滤与限制。比如从指定URL地址获取网页文本内…...
Qt5开发及实例V2.0-第十八章-Qt-MyselfQQ实例
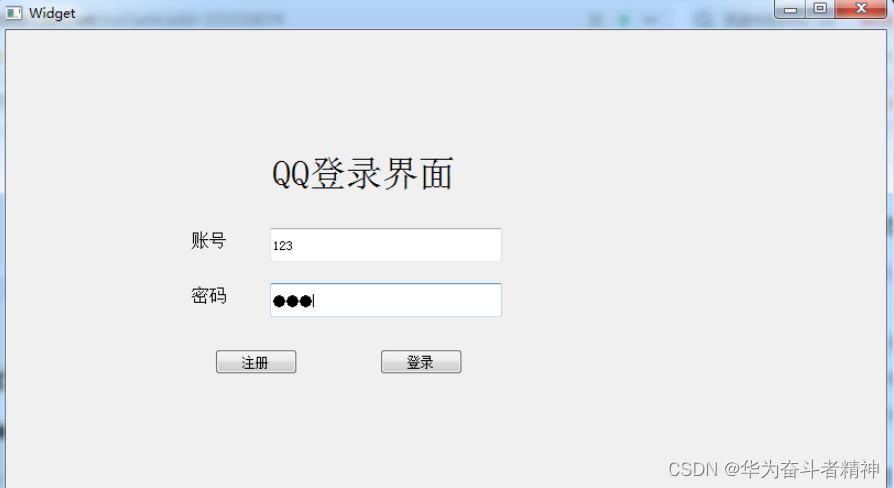
Qt5开发及实例V2.0-第十八章-Qt-MyselfQQ实例 第18章-Qt MyselfQQ18.1 概述18.2 、发送文件18.3 、接收文件18.4 、保证传输的安全和稳定18.5 、总结 本章相关例程源码下载1.Qt5开发及实例_CH1801.rar 下载 第18章-Qt MyselfQQ 18.1 概述 MyselfQQ是一个基于Qt5框架开发的轻量…...

当下IT测试技术员的求职困境
从去年被裁到现在,自由职业的我已经有一年没有按部就班打卡上班了。期间也面试了一些岗位,有首轮就挂的,也有顺利到谈薪阶段最后拿了offer的,不过最后选择了拒绝。 基于自己近一年的面试求职经历,我想聊聊当下大家在求…...

MR混合现实情景实训教学
MR混合现实技术是一种将虚拟现实与现实场景相融合的创新技术,可以广泛应用于各个领域。其中,混合现实情景实训教学是MR技术的一个重要应用场景。 在医学专业方面,医学生常常需要通过实际操作来提升自己的技能水平,然而传统的实训方…...

嵌入式C++总结
1、new delete与malloc free区别 new delete是运算符,malloc free是函数。 前者不需要传入大小,后者需要。 前者会调用构造、析构函数,后者不会。 前者不需要强制转换,后者需要。 2、智能指针 智能指针是避免忘记释放动态申请对象…...
C语言之内存函数篇(3)
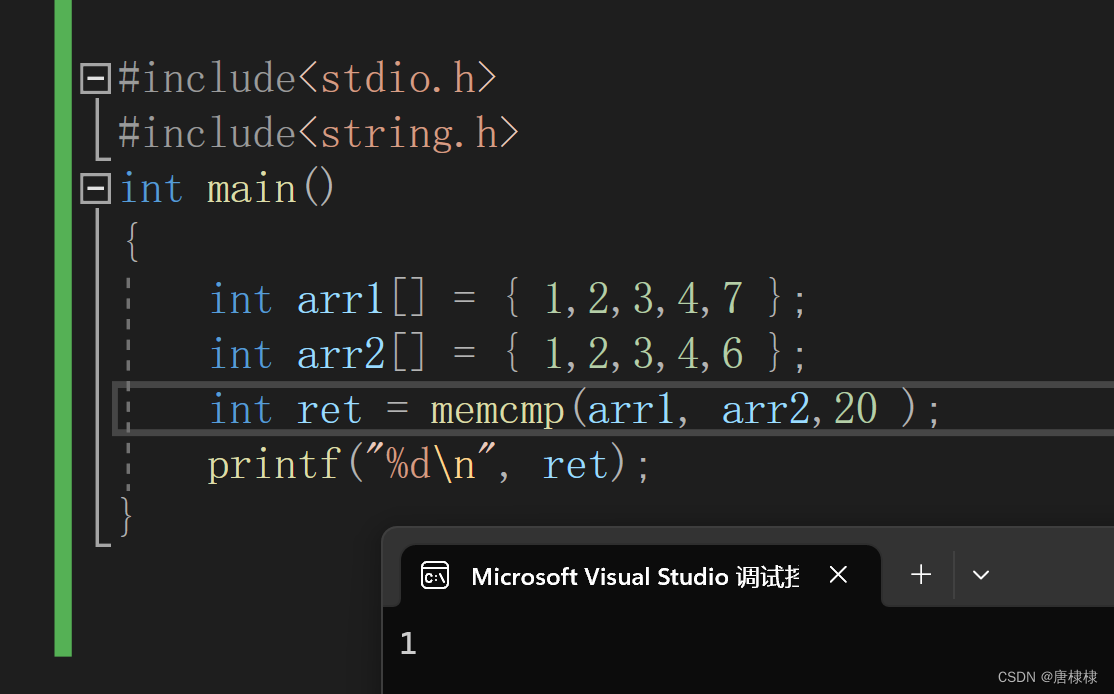
目录 memcpy memcpy的使用 memcpy的模拟实现 NO1. NO2. memcpy可否实现重叠空间的拷贝 my_memcpy memcpy memmove memmove memmove 分析 代码 memset memset的使用 memcmp memcmp的使用 <0 0 >0 今天我们继续介绍几个重要的内存操作函数。&…...

java面试题-学成在线项目
1、详细说说你的项目吧 从以下几个方面进行项目介绍: 1、项目的背景,包括:是自研还是外包、什么业务、服务的客户群是谁、谁去运营等问题。 2、项目的业务流程 3、项目的功能模块 4、项目的技术架构 5、个人工作职责 6、个人负责模块的详细说…...

ViewBinding——Android之视图绑定
高版本的gradle不再支持 kotlin-android-extensions插件,因此view的绑定方式也有所改变。 1.启用视图绑定 android {...viewBinding {enabled true}} 如果想在生成绑定类时忽略某个布局文件,请将 tools:viewBindingIgnore"true" 属性添加到…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...
