高教杯数学建模A题程序设计要点与思路
- 2023 年是我最后一次参加 高教杯大学生数学建模竞赛 以后不会再参加了(大四参加意义不太,研究生有研究生的数学建模大赛)
- 很遗憾 由于各种原因 我们没有能够完成赛题
- 2022 年 美赛 2022年 Mathor Cup 2022 年国赛 2022 亚太杯 2023年 美赛 2023年 国赛
- 我和我的朋友一共参加了6次比赛
- 6次比赛 我交到了很好的朋友
- 然鹅 成绩比较惨淡 S*1 H*1 省三一次
- 唉,数模啊数模,很难说出口啊
- 今年本来特别有信心的,但是,唉,。。。A题,我的痛
- 为了研究A题
- 我们先后学习了
- 数理方程
- 数值分析
- 数值仿真
- 优化算法
- 稳定性的理论
- ......
- 就是想在2023 年A题大展身手,可惜啊可惜
- 光学 我的痛
- 真的很难过 心里一直算算的 感觉对不起朋友
- 确实是我自己不行
- 自己不行啊
- 我们先后学习了
-
- 暑假刚做过手术
- 暑假手术之前去了一些大学
- 一个优营也没有拿到,毕竟年龄有点小,基础不扎实
- 本来计划三年物理系毕业然后转强基计划然后深造的,因为我真的修完了课程。
- 但是计划有变啊。三年毕竟不够扎实
- 现在去选了 核与粒子物理 欢迎交流
- 最后一次参加数学建模是2023UPC 好像是11月第一个周末
- 加油
- 本文主要介绍这几个极其重要的程序设计思路,欢迎大家参考,引用
- 真的,毕竟百度也是可以引用的嘛
- 不引用我绝对不会在意的
数值常微分
参考书目
- 微分方程的数值解法与程序实现 华冬英 李祥贵
- 量子物理学中的常用算法与程序 井孝功 赵永芳 蒿凤有
- 稳定性的理论,方法和应用
- 微分方程 动力系统与混沌导论
简介
- 很多同学学习数值分析,都是 高斯消元 牛顿迭代 然后...
- 譬如我写过的一篇博客
Python牛顿迭代法的应用
追赶法(Thomas) 雅克比迭代(Jacobi) 高斯迭代(Gauss) 的C++实现
- 其实我不建议这样,为什么呢?
- 函数零点(非线性方程组的解)的求法非常重要,是现代科学计算的基础性内容,但是,这并不意味着我们必须从这些知识学起,原因有2
- 1.简单的方法收敛条件严格,具体情况需要具体分析,大概率需要更强的算法
- 2.已经有封装好的先进方法,不应该在基础方法上浪费时间
- 包括程序设计的时间
- 包括程序运行时,因为方法优化不得当导致的计算增加时间
- 函数零点(非线性方程组的解)的求法非常重要,是现代科学计算的基础性内容,但是,这并不意味着我们必须从这些知识学起,原因有2
- 数值常微分方程求解包括下面两类
- 边值问题的求解(本征值问题的求解)
- 初值问题的求解
- 辛算法
边值问题
- 这个问题非常常见
- 学习过数学物理方程的同学或者泛函分析的课程对此一定印象深刻
- 我写过的一些博客有
变分原理与边值问题的计算机处理
计算物理专题:双向打靶法解决本征值问题
计算物理专题:有限差分法解决本征值问题
Numerov算法解一维无限深势阱的问题 (含量子力学导论)
- 你可以使用matlab Pdetool 辅助求解 这也是非常棒的选择
- 具体的代码就不放在这里了,因为这个难度比较低,关键是验证的难度很低,图一画就知道算得对不对了,也是暴力求解可以解决的问题,完全没有压力
初值问题
- 这个问题是最常见的问题 譬如2022 年高教杯A题
- 如果读者对 动力系统有一定了解的话 这个问题可以做的非常漂亮
- 我个人认为应当从动力系统学起,这样的话分析解的稳定性就会更完整更合理,而不是放一个试验方程的小招就结束了
- 初值问题的解法分为两类
- 隐式解法
- 显式解法
- 简单得说,显式解法指的是解的当前步完全由解的前几步决定
- 而隐式解法指的是
- 只能得到以当前解为未知数的一个方程,必须求解这个方程才能得到当前解
- 这也就是为什么我不建议花太多时间在高斯迭代,牛顿迭代上的原因。
- 对于单个的函数,分析算法的稳定是方便的,但是实际问题中我们更关注的是大型方程组的求解,他们往往是非线性的,耦合的,难以分析的,这时解法的稳定性分析难度会非常得大,不如采取:软件+验证的方法
- 我写过的相关的一些博客我列在这里,具体的代码我就不反复引用了
Python数值分析案例01--------四阶龙格库塔法解抛体运动
常微分方程的龙格库塔显式与隐式解法
- 尤其是第二篇文章,非常值得好好阅读,
- 直接引用相关的方法即可,均经过了实践的检验
- 包含了一个并行加速的例子,可能需要先学习一下multiprocessing
- 提示:每次求解必须有稳定性的分析,没有稳定性的分析,你的解的意义何在?可信度何在?
哈密顿系统的辛算法
- 这是很出彩的一个地方
- 如果有同学能在数学建模竞赛中实现这一点,我想是极其棒的一件事情,而且我从未见过有很好的论文在本科生竞赛中实现这一点,这是很不现代的
- 在这里我就不赘述他的优点在什么地方了,较为复杂,公式也很多,
- 但是只说一句话吧,这个方法算得出彩,就行了
- 这是我写的一篇博客,可以看看,这非常的基础,你需要很好阅读参考书才能很好得应用他
自洽可分的哈密顿系统的辛算法
参考文献
- 量子系统的辛算法 丁培柱
数值积分
- 数值积分常常在数学建模竞赛的某一处出现,还是非常重要的
蒙特卡洛积分方法
- 蒙特卡洛积分处理高维积分的效果会更优秀一点,在我很近的一篇文章中提到了对比,但只是很粗略的一笔蒙特卡洛方法的数学基础-1
- 所以如果只是处于装一下的需要的话,完全没有必要写上去
近似积分方法
- 大家常用的 矩形近似法 梯形近似法 辛普森近似 都属于这一类
- 我想,如果是已知了具体函数形式的话,使用外推法会更好一些
计算物理专题:高维Romberg数值积分方法
- 但很多时候,我们只有每个点的函数值,那么还是使用辛普森方法或者更高阶的方法要好
中心差分式
- 中心差分式是大家都很熟悉的东西了
- 我需要提到的一点是,你选取的方法的精度尽量要高一些,譬如
- 目标是 二阶近似
- 某一步需要用到中心差分值的方法是四阶近似的
- 那么你的中心差分式精度的选择应该不低于四阶才好
数值偏微分
- 这也是常考的问题
- 但是数值偏微分方程的求解极其得复杂,稳定性特别难以分析,我举一个 用迎风法求解抛物型方程的例子
import numpy as np
import matplotlib.pyplot as plt#\frac{\partial u}{\partial t} = \lambda(
#\frac{\partial^2 u}{\partial x^2} +
#\frac{\partial^2 u}{\partial y^2}
#) + q_vclass projequation2D():def __init__(self, Lambda=1, qv = lambda t, x, y:0,X_start=0, X_end=1,Y_start=0, Y_end=1,T_start=0, T_end=1,dx = 0.05,dy = 0.05,dt = 0.01):#c = lambda x,y,t:(?)self.Lambda = Lambdaself.qv = qvself.dx = dxself.dy = dyself.dt = dtself.X_start = X_startself.Y_start = Y_startself.T_start = T_startself.X_end = X_endself.Y_end = Y_endself.T_end = T_endself.X = np.arange(X_start, X_end, dx)self.Y = np.arange(Y_start, Y_end, dy)self.T = np.arange(T_start, T_end, dt)self.results = np.zeros((len(self.T), len(self.X), len(self.Y)))self.startresults()def initcondition_0(self):X_num = len(self.X)Y_num = len(self.Y)test_fun = lambda x,y: np.sin(5*x)*np.cos(5*y)for ix in range(X_num):for iy in range(Y_num):self.results[0][ix][iy] == test_fun(self.X[ix], self.Y[iy])def boundarycondition_left(self):Y_num = len(self.Y)T_num = len(self.T)for it in range(T_num):for iy in range(Y_num):self.results[it][0][iy] = 25def boundarycondition_right(self): Y_num = len(self.Y)T_num = len(self.T)for it in range(T_num):for iy in range(Y_num):self.results[it][-1][iy] = 25def boundarycondition_up(self):X_num = len(self.X)T_num = len(self.T)for it in range(T_num):for iy in range(X_num):self.results[it][iy][-1] = 25def boundarycondition_down(self):X_num = len(self.X)T_num = len(self.T)for it in range(T_num):for iy in range(X_num):self.results[it][iy][0] = 25def startresults(self):self.initcondition_0()self.boundarycondition_left()self.boundarycondition_right()self.boundarycondition_up()self.boundarycondition_down()def Upwind3P(self):for Ti in range(1, len(self.T)):for Xi in range(1, len(self.X)-1):for Yi in range(1, len(self.Y)-1):rx = self.Lambda * self.dt/(self.dx)**2ry = self.Lambda * self.dt/(self.dy)**2self.results[Ti][Xi][Yi] = \rx * (self.results[Ti-1][Xi-1][Yi]+self.results[Ti-1][Xi+1][Yi])+\2* (1-rx-ry) *self.results[Ti-1][Xi][Yi]+\ry * (self.results[Ti-1][Xi][Yi-1]+self.results[Ti-1][Xi][Yi+1])-\self.results[Ti-2][Xi][Yi]return self.resultsdef show_wave(self):fig = plt.figure(figsize=(8,8))ax1 = fig.add_subplot(111, projection='3d')x, y = np.meshgrid(self.X, self.Y)for time in range(len(self.T)):ax1.plot_surface(x, y, self.results[time, :, :],rstride=2, cstride=2, cmap='rainbow')plt.title("time:" + str(self.T[time]))plt.pause(0.5)plt.cla()c = projequation2D()
u = c.Upwind3P()
c.show_wave()
- 再来一个解波动方程的例子
import numpy as np
import matplotlib.pyplot as plt#\frac{\partial^2 u}{\partial t^2} = c^2 (
#\frac{\partial^2 u}{\partial x^2} +
#\frac{\partial^2 u}{\partial y^2}
#)class waveequation2D():def __init__(self, c,X_start=0, X_end=1,Y_start=0, Y_end=1,T_start=0, T_end=1.01,dx = 0.01,dy = 0.01,dt = 0.01):#c = lambda x,y,t:(?)self.c = cself.dx = dxself.dy = dyself.dt = dtself.X_start = X_startself.Y_start = Y_startself.T_start = T_startself.X_end = X_endself.Y_end = Y_endself.T_end = T_endself.X = np.arange(X_start, X_end, dx)self.Y = np.arange(Y_start, Y_end, dy)self.T = np.arange(T_start, T_end, dt)self.results = np.zeros((len(self.T), len(self.X), len(self.Y)))self.startresults()def initcondition_0(self, x, y):return np.sin(10*x)def initcondition_1(self, x, y):return np.sin(10*x)def boundarycondition_left(self, t, x, y):return (np.sin(10*y))[0]def boundarycondition_right(self, t, x, y): return (np.sin(10*y))[0]def boundarycondition_up(self, t, x, y):return (np.sin(10*x))[0]def boundarycondition_down(self, t, x, y):return (np.sin(10*x))[0]def startresults(self):x, y = np.meshgrid(self.X, self.Y)self.results[0] = self.initcondition_0(x, y)self.results[1] = self.initcondition_1(x, y)t, x, y = np.meshgrid(self.T, self.X, self.Y)self.results[:, 0, :] = self.boundarycondition_left(t, self.X_start, y)self.results[:, -1, :] = self.boundarycondition_right(t, self.X_end, y)self.results[:, :, -1] = self.boundarycondition_up(t, x, self.Y_end)self.results[:, :, 0] = self.boundarycondition_down(t, x, self.Y_start)def test_stability(self, x, y, t):test = 4*self.dt**2*self.c(x, y, t)**2/(self.dx**2 + self.dy**2)if test<=1:return Trueelse:print("unstable in x:", x, "y:", y, "t:", t)return Falsedef Upwind3P(self):for Ti in range(2, len(self.T)):for Xi in range(1, len(self.X)-1):for Yi in range(1, len(self.Y)-1):rx = self.c(self.X[Xi], self.Y[Yi], self.T[Ti])**2 * self.dt**2/self.dx**2ry = self.c(self.X[Xi], self.Y[Yi], self.T[Ti])**2 * self.dt**2/self.dy**2self.results[Ti][Xi][Yi] = \rx * (self.results[Ti-1][Xi-1][Yi]+self.results[Ti-1][Xi+1][Yi])+\2* (1-rx-ry) *self.results[Ti-1][Xi][Yi]+\ry * (self.results[Ti-1][Xi][Yi-1]+self.results[Ti-1][Xi][Yi+1])-\self.results[Ti-2][Xi][Yi]
## self.test_stability(self.X[Xi],self.Y[Yi],self.T[Ti]) return self.resultsdef show_wave(self):fig = plt.figure(figsize=(8,12))ax1 = fig.add_subplot(121, projection='3d')ax2 = fig.add_subplot(122, projection='3d')x, y = np.meshgrid(self.X, self.Y)for time in range(len(self.T)):ax1.plot_surface(x, y, self.results[time, :, :],rstride=2, cstride=2, cmap='rainbow')ax2.plot_wireframe(x, y, self.results[time, :, :],rstride=2, cstride=2, linewidth=1, cmap='rainbow')plt.title("time:" + str(self.T[time]))plt.pause(0.01)plt.cla()def test_fun(x, y, t):return 1c = waveequation2D(c=test_fun)
u = c.Upwind3P()
c.show_wave()
- 所以一般建议使用Matlab 中的pdetool 求解
- 这是我写的两篇博客,可以参考
典型的偏微分方程数值解法
二维Poisson方程五点差分格式与Python实现
- 一定要仔细阅读有关书籍,否则很难做出比较好的成果
参考书目
- 偏微分方程的数值解法(第三版) 陆金甫
- 特殊函数概论 王竹溪
- 数学物理方法与仿真(第三版) 杨华军
- 科学计算中的偏微分方程有限差分法 张文生
优化算法
- 这是是数学建模的核心,优化求解
- 一般而言,很多问题可以做凸优化
- 但是,数学建模中的优化问题往往不能...
- 所以,要么二分法全局搜索,要么智能求解吧
- 最近会写一些相关的博客,就不具体演示了。也可以去我的博客下面找......
- 写完博客,心情舒畅不少
相关文章:

高教杯数学建模A题程序设计要点与思路
2023 年是我最后一次参加 高教杯大学生数学建模竞赛 以后不会再参加了(大四参加意义不太,研究生有研究生的数学建模大赛) 很遗憾 由于各种原因 我们没有能够完成赛题2022 年 美赛 2022年 Mathor Cup 2022 年国赛 2022 亚太杯 2023年 美赛 202…...

Spring Boot的新篇章:探索2.0版的创新功能
文章目录 引言1. Spring Boot 2.0的响应式编程2. 自动配置的改进3. Spring Boot 2.0的嵌入式Web服务器4. Spring Boot 2.0的Actuator端点5. Spring Boot 2.0的Spring Data改进6. Spring Boot 2.0的安全性增强7. Spring Boot 2.0的监控和追踪8. Spring Boot 2.0的测试改进结论 &…...
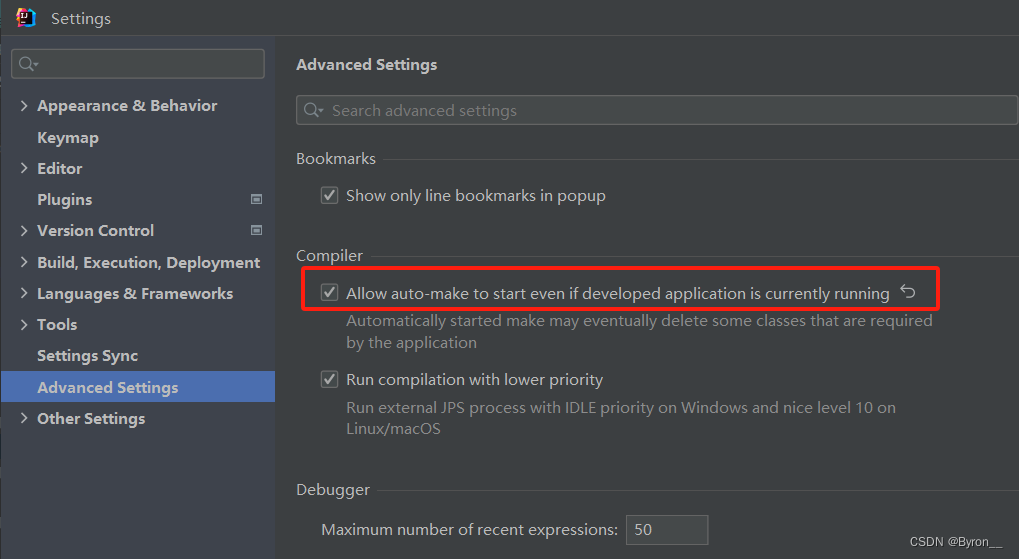
5、SpringBoot_热部署
六、热部署 1.热部署概述 概述:程序更改后,不需要重新启动服务器也能够实现动态更新 springboot 项目如何实现热部署? tomcat 已经内置到项目容器中了希望tomcat监听外部程序变化通过新建一个程序来监控你代码的变化 2.依赖导入 依赖 <…...
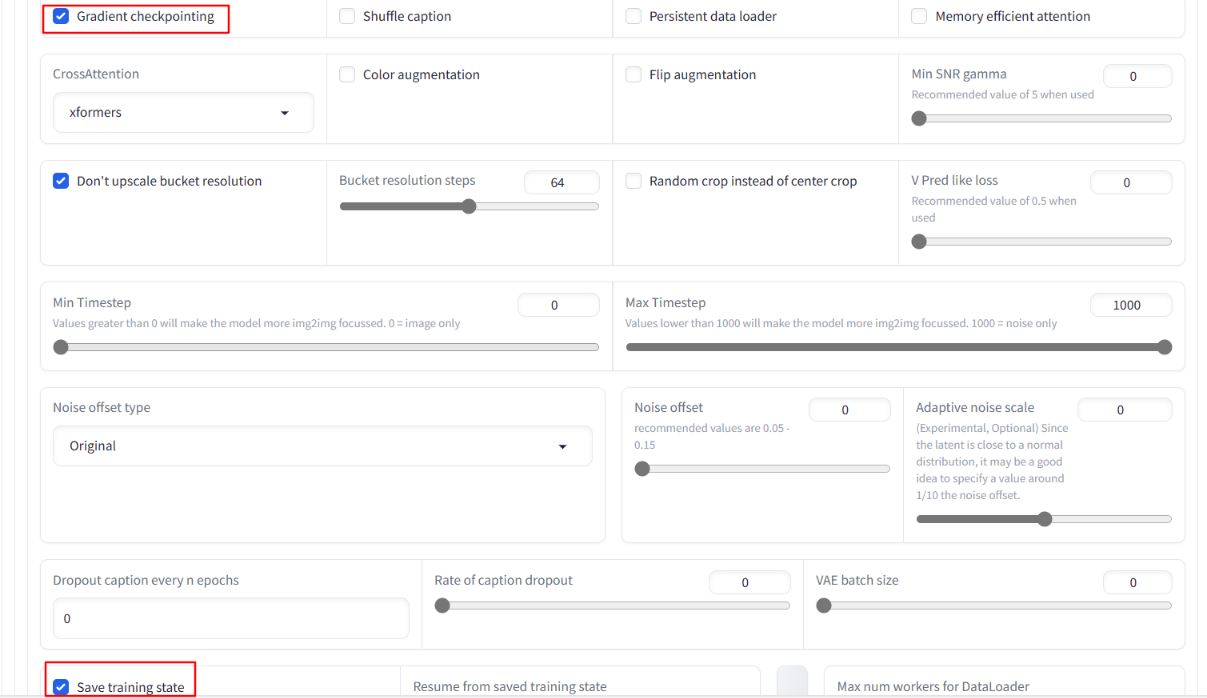
【kohya】训练自己的LoRA模型
文章目录 序言准备环境准备图片处理图片下载kohya_ss代码修改pyvenv.cfg启动界面访问地址生成字幕准备训练的文件夹配置训练参数开始训练遇到的问题: 序言 在把玩stable diffusion的webUI和comfyUI后,思考着自己也微调一个个性化风格的checkpoint、LyCO…...
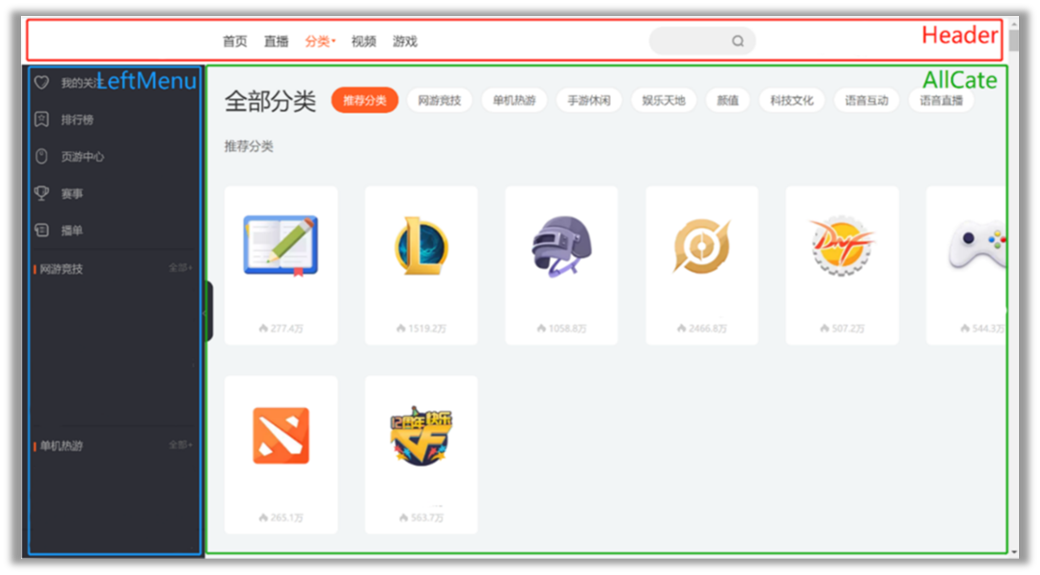
[尚硅谷React笔记]——第1章 React简介
目录: 第1章 React简介 React的基本使用:虚拟DOM的两种创建方式: 使用jsx创建虚拟DOM使用js创建虚拟DOM(一般不用)虚拟DOM与真实DOM:React JSX:JSX练习:模块与组件、模块化与组件化的理解 模块组件模块化组件化 第1章 React简介 中文官网: …...

Debezium系列之:快照参数详解
Debezium系列之:快照参数详解 一、snapshot.select.statement.overrides二、min.row.count.to.stream.results三、snapshot.delay.ms四、snapshot.fetch.size五、snapshot.lock.timeout.ms六、incremental.snapshot.allow.schema.changes七、incremental.snapshot.chunk.size八…...

redis单机版搭建
title: “Redis单机版搭建” createTime: 2022-01-04T20:43:1108:00 updateTime: 2022-01-04T20:43:1108:00 draft: false author: “name” tags: [“redis”] categories: [“install”] description: “测试的” redis单机版搭建 安装环境 redis版本redis-5.0.7虚拟机系统…...

物联网边缘网关
物联网边缘网关 边缘网关的定义边缘网关的分类边缘计算网关平台相关产品有哪些 百度边缘计算平台(BIE)华为边缘计算平台(IEF)产品应用拓扑图产品价格区间...

docker部署springboot程序时遇到的network问题
对应问题,因为刚开始接触docker,所以问题可能比较简单,但是做个记录 1、启动一个springboot项目获取本地ip的时候获取到的是172.17.0.x这个ip;在使用一些注册中心,mq的时候又要表明自己的本机器ip的时候会比较头疼&…...
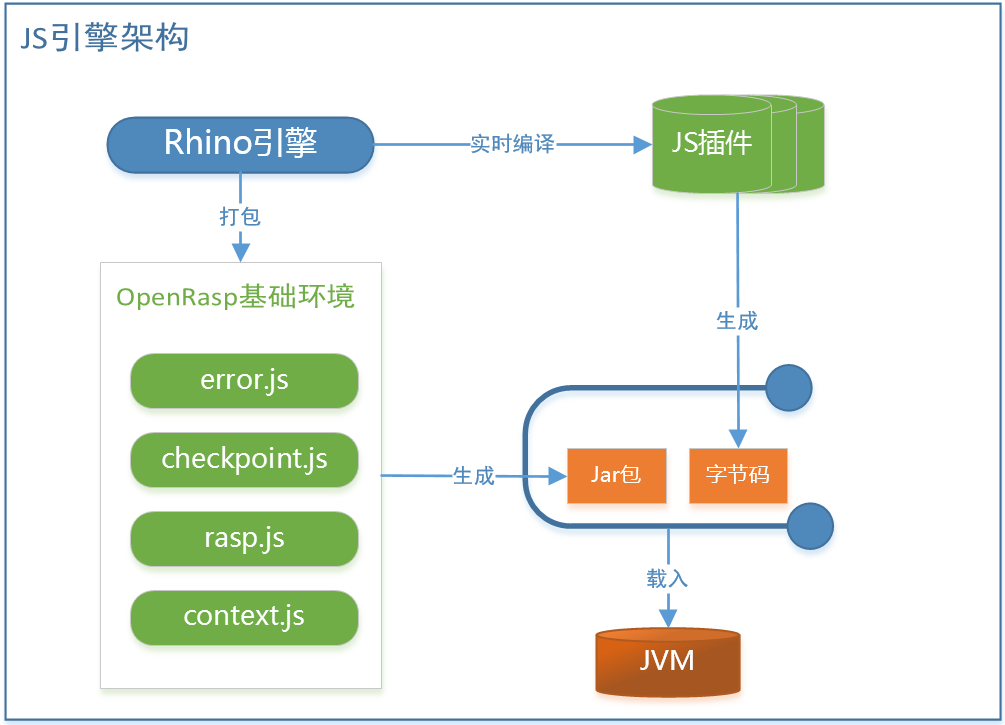
RASP hook插桩原理解析
javaagent技术,实现提前加载类字节码实现hook,插桩技术 javassist技术ASM字节码技术 像加载jar,有两种方式 premain启动前加载:每次变动jar包内容,都需要进行重启服务器利用java的动态attch加载原理,采用pr…...
Pygame中Sprite的使用方法6-5
3 碰撞检测 蓝色方块会随着鼠标移动,当碰到绿色方块时,则当前分数加1,当碰到红色方块时,当前分数减1。因为要随时进行碰撞检测,因此需要在while True循环中实现以下功能。 3.1 蓝色方块随鼠标移动 将蓝色方块的位置…...

浅谈为什么多态只能是指针或引用
其实在很早之前,我一直没有注意到这个问题,直到今天碰见了一道题,顺便前面的博客中,继承写到,子类中不包含父类,子类只是继承了父类的成员变量和函数,由这一点,引发了我对切片以及赋…...

js看代码说输出
目录 原型 Function与Object new fn() 原型链 constructor function.length 默认参数:第一个具有默认值之前的参数个数 剩余参数:不算进length 闭包 循环中 函数工厂:形参传递 IIFE:匿名闭包 let:闭包 forEach()&am…...

Java笔记:使用javassist修改class文件内方法
1.前言 在工作突然有一个需求。线上运维的一个tomcat的web项目,运行的程序不正常。需要修改代码。可是这个项目代码非常的老,并且公司存储的源代码跟线上的不一致。 我了个擦,没有源代码但是还要结局客户的问题。只能到线上将对应程序的clas…...
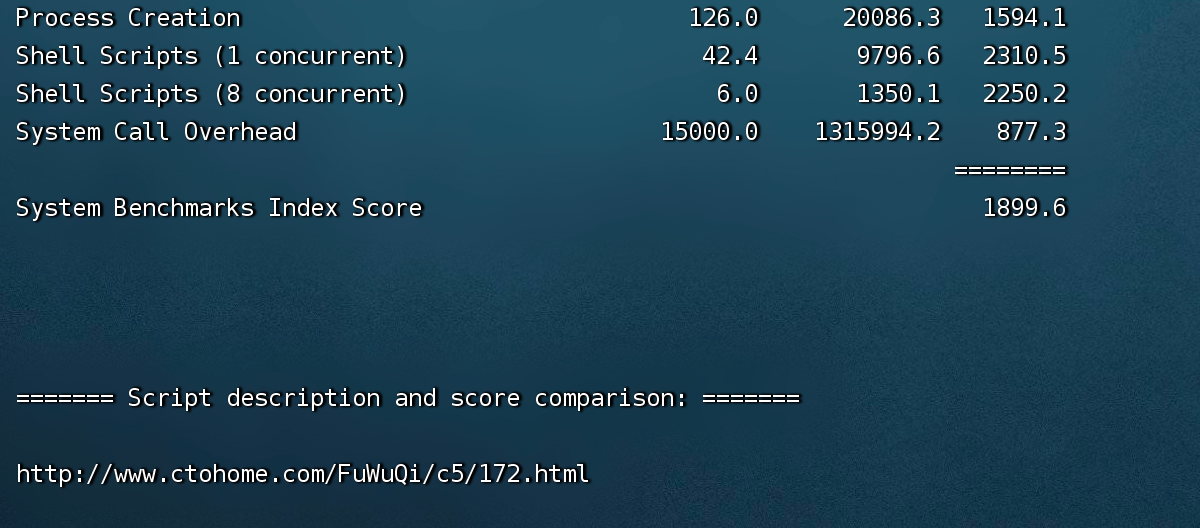
华为云云耀云服务器L实例评测 |云服务器性能评测
通过上一篇文章华为云云耀云服务器 L 实例评测 |云服务器选购,我已经购买了一台 Centos 系统的云耀云服务器 L 实例。 在获得云耀云服务器 L 实例后,首要任务是熟悉云耀云服务器 L 实例的性能,对云耀云服务器 L 实例的性能进行测…...

iphone的safari浏览器实现全屏的pwa模式,并修改顶部状态栏背景颜色
要想修改顶部背景颜色,需要用到这个属性:content就是你要设置的颜色 <!-- 状态栏的背景色 --><meta name"theme-color" content"#f8f8f8" /> 然后再加上下面的设置: <!-- 网站开启对 web app 程序的支持…...
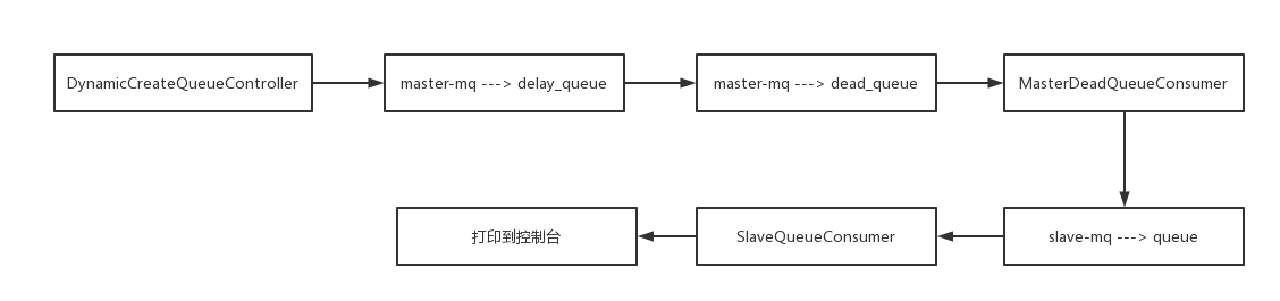
springboot对接rabbitmq并且实现动态创建队列和消费
背景 1、对接多个节点上的MQ(如master-MQ,slave-MQ),若读者需要自己模拟出两个MQ,可以部署多个VM然后参考 docker 安装rabbitmq_Steven-Russell的博客-CSDN博客 2、队列名称不是固定的,需要接受外部参数&…...

Spring的后处理器-BeanFactoryPostprocessor
目录 Spring后处理器 Bean工厂后处理器-BeanFactoryPostProcessor 修改beanDefinition对象 添加beanDefiniton对象 方法一 方法二 自定义Component Spring后处理器 Spring后处理器是Spring对外开放的重要拓展点(让我们可以用添加自己的逻辑)&…...
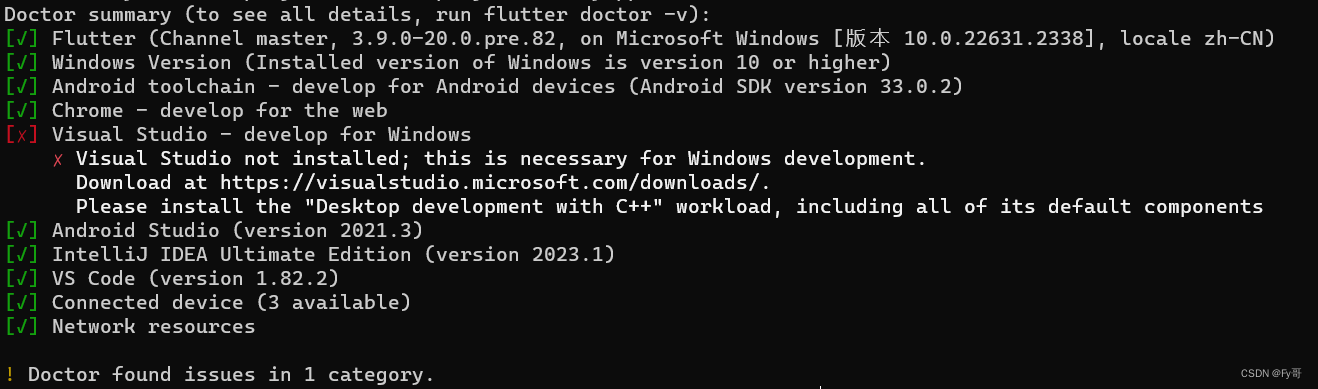
Flutter 必备知识点
Flutter 升级 确保在项目根目录下(含有 pubspec.yaml 的文件夹) 在命令行中输入命令: flutter channel输出: Flutter channels: * mastermainbetastable这个可以在 pubspec.yaml 中查看: 切换分支也很简单…...
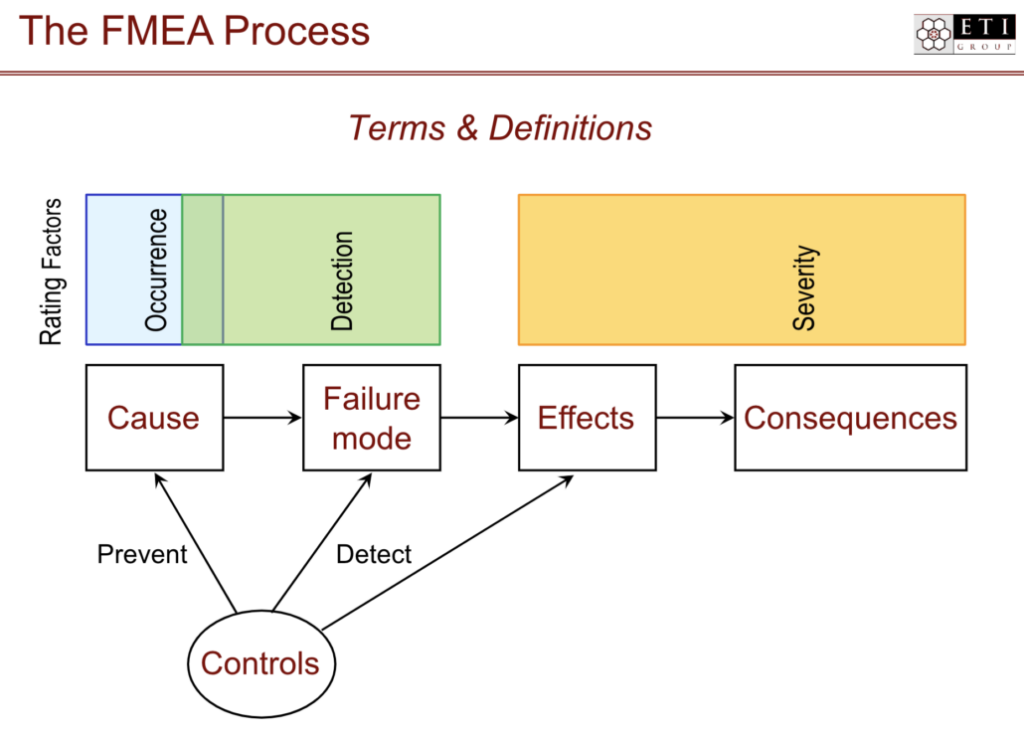
什么是FMEA(失效模式和影响分析)?
失效模式和影响分析(FMEA)是一个在开发阶段,用于确定产品或流程可能的风险和失败点的有条理的过程。FMEA团队会研究失效模式,也就是产品或流程中可能出错的地方,以及这些失效可能带来的影响(如风险、损害、…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
