算法通过村第八关-树(深度优先)白银笔记|深度和高度问题
文章目录
- 前言
- 1. 最大深度问题
- 2. 判断平衡树
- 3. 最小深度
- 4. N叉树的最大深度
- 总结
前言
提示:我的整个生命,只是一场为了提升社会地位的低俗斗争。--埃莱娜·费兰特《失踪的孩子》
这一关我们看一些比较特别的题目,关于二叉树的深度和高度问题。这些对递归的考察更高些,要注意了。
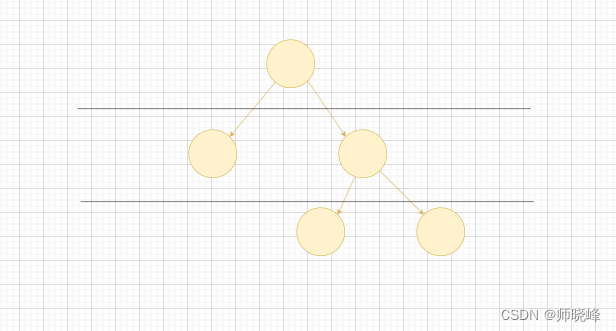
给你一个二叉树:
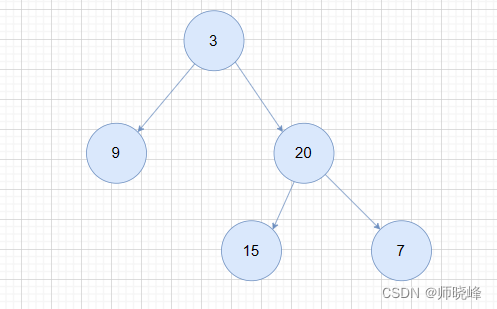
我们看下力扣的相关题目,这些是关于深度和高度的问题。
推荐题目⭐⭐⭐⭐:
104. 二叉树的最大深度 - 力扣(LeetCode)
110. 平衡二叉树 - 力扣(LeetCode)
111. 二叉树的最小深度 - 力扣(LeetCode)
1. 最大深度问题
参考题目介绍:104. 二叉树的最大深度 - 力扣(LeetCode)

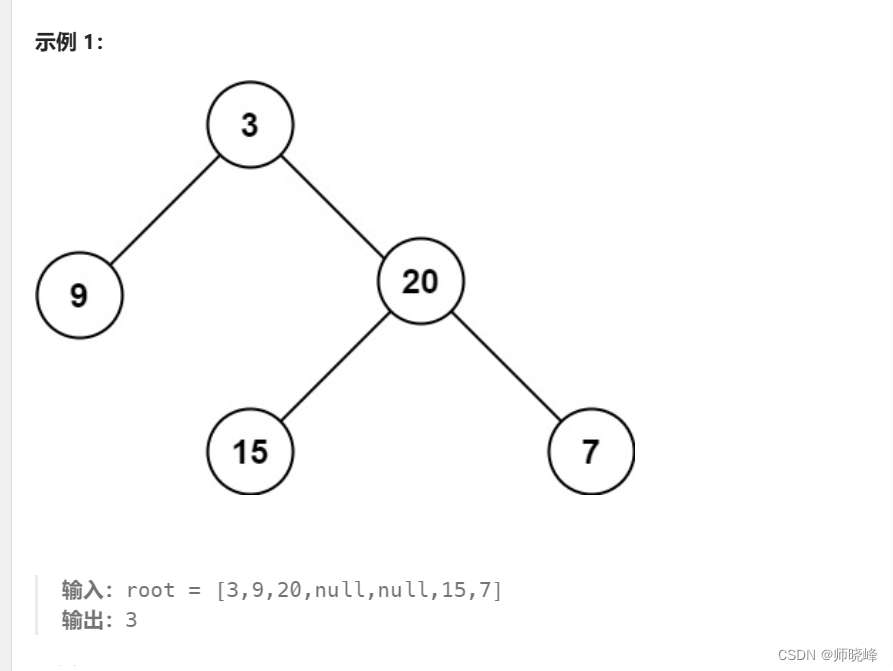
首先最大深度:根节点到最远叶子节点的最长路径上的节点数。说明叶子节点是没有子节点的。
我们看看下面这些。(上图的最大深度为3)
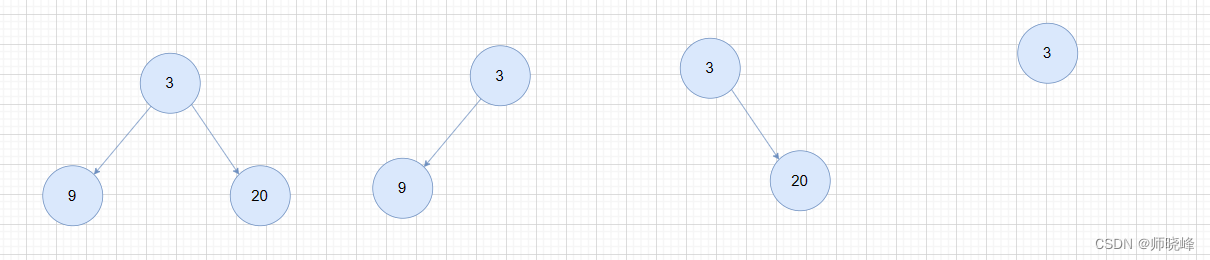
对于node(3),最大深度自然是左右子节点+1,左右子节点有可能为空,只要有一个,树的最大高度就是1 + 1 = 2。然后再增加几个节点:
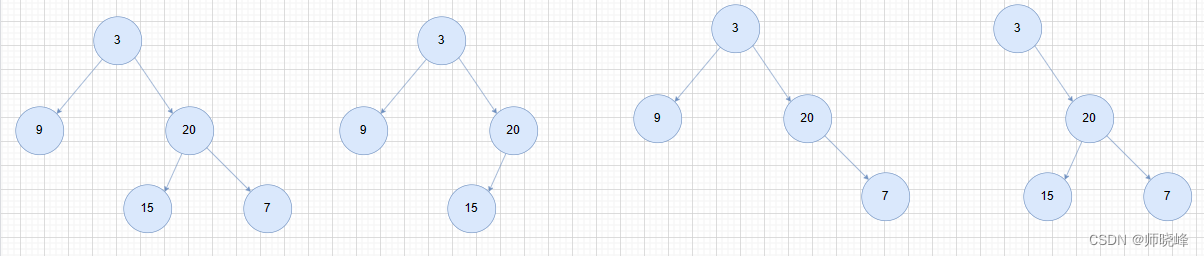
很显然相对于node(20),最大的深度自然是左右子节点+1,左右子节点有可能为空,只要右一个,树的最大高度就是1 + 1 = 2,用代码表示就是:
int depth = 1 + math(leftDepth,rightDepth);
对于3,则是左右子树深度最大的那个再加1,具体谁的更大,则不必管旭,所以对于node(3)的逻辑判断就是:
int leftDepth = getDepth(root.left); //左
int rightDepth = getDepth(root.right); // 右
int depth = 1 + math(leftDept,rightDept); // 中
那么什么时候结束呢?这里仍然是root == null 返回0就行了,至于入参,自然是要处理的子树的根节点root,而返回值则是当前root所在子树的最大高度,所以合在一起就是:
/*** 通过递归计算二叉树的深度** @param root* @return*/public static int maxDepth_1(TreeNode root) {if(root == null) {return 0;}int leftDepth = maxDepth_1(root.left);int rightDepth = maxDepth_1(root.right);return Math.max(leftDepth, rightDepth) + 1;}
上面代码先拿到左右子树的结果,再计算Math.max(left,right) + 1,本质上和后序遍历一样,一次者可以看做事后序遍历的扩展问题。
我们继续看这个题目,如果我们确定树最大有几层是不是也确定了最大深度呢?当然,另一个思路不就来了,我们直接套用层序遍历的代码:
具体细节注意一下:我们这里获取层数,每获取一层,就加一。
/*** 通过层次遍历来求最大深度** @param root* @return*/public static int maxDepth_2(TreeNode root) {// 校验参数if (root == null){return 0;}// 创建空间int res = 0;Queue<TreeNode> queue = new LinkedList<TreeNode>();// 根节点入队,不断的遍历根节点queue.offer(root);while(!queue.isEmpty()){// 获取到每层多少个int size = queue.size();// size == 0 说明这一层遍历完了while(size > 0){// 遍历TreeNode node = queue.poll();if (node.left != null){queue.offer(node.left);}if (node.right != null){queue.offer(node.right);}size--;}res++;}return res;}
2. 判断平衡树
参考题目介绍:110. 平衡二叉树 - 力扣(LeetCode)

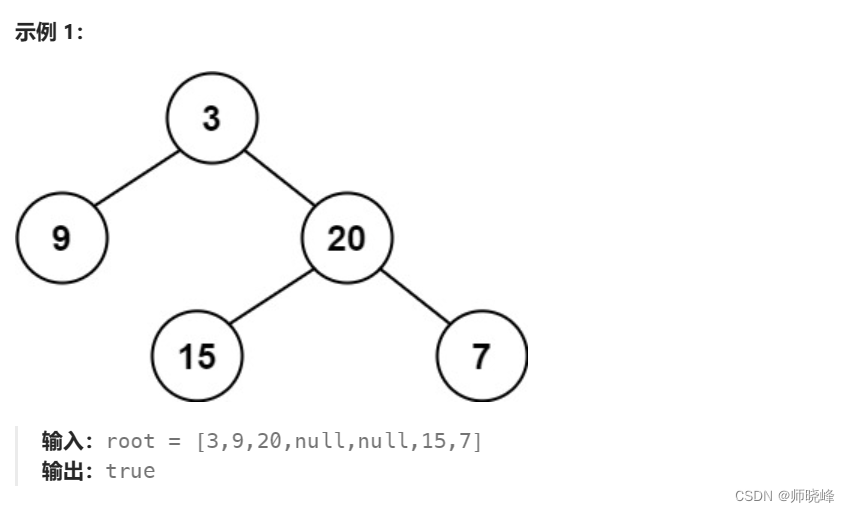
补充一个知识点:高度和深度怎么区分?
- 二叉树节点的深度:从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:从该节点到叶子节点的最长简单路径边的条数。
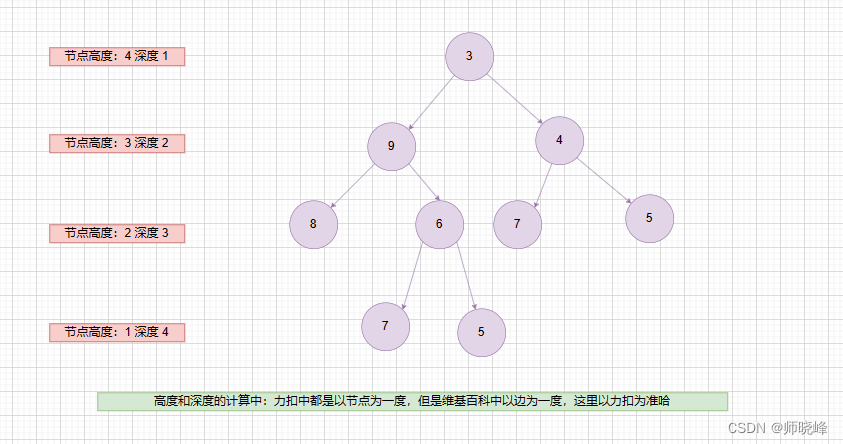
关于根节点的深度是1还是0的问题,不同的地方标准不一样,力扣的题目中都是以根节点的深度为1,其他的我们先不管。
我们接着看一下这个问题:

很显然只要有两次的时候一定是平衡的,因为对于node(3),左右孩子如果只有一个,呢么高度差就是1;如果左右孩子都没有或者都有,则高度差为0。但是如果再加一层呢?
看下图:
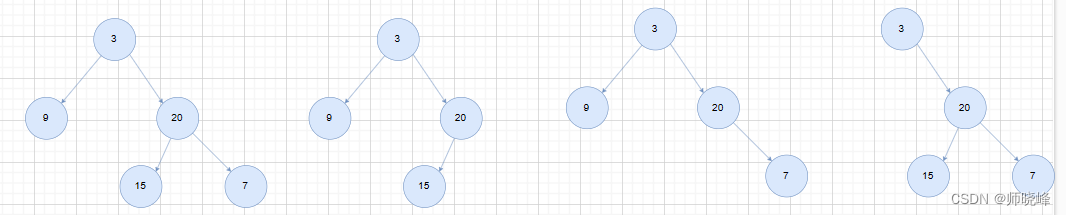
对于node(3),需要同时知道自己左右子树的最大高度差是否< 2.
- 当节点root左/右子树的高度差 < 2,则返回节点root的左右子树中最大高度+1(max(left,right) + 1);参考上面的深度和高度对比图思考下,这里为什么取最大高度?
- 当节点root左/右子树的高度差 >= 2;则返回-1,代表此树已经不是平衡树了。
也是就是说:
int left = recur(root.left);
int right = recur(root.right);
return Math.abs(left - right) < 2 ? Math.max(left,right) + 1:-1;
我们此时已经写出了核心代码,假设子树已经不平衡了,我们就不需要再递归下去而是直接返回就行了。例如这个树中的节点20:
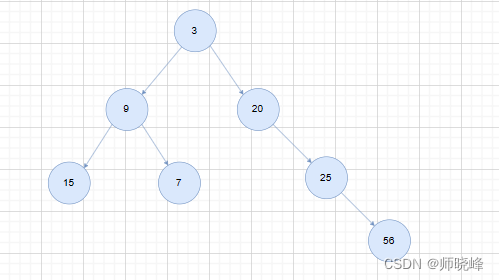
综合考虑几种情况,我们看下完整的代码:
/*** 方法1 自下而上** @param root* @return*/public static boolean isBalanced_1(TreeNode root) {return recur(root) == -1;}public static int recur(TreeNode root) {if (root == null){return 0;}int left = recur(root.left);if (left == -1){return -1;}int right = recur(root.right);if (right == -1){return -1;}return Math.abs(left - right) < 2 ? Math.max(left,right) + 1: -1;}
/*** 2.自上而下** @param root* @return*/public static boolean isBalanced_2(TreeNode root) {if (root == null){return true;}return Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced_2(root.left) && isBalanced_2(root.right);}public static int depth(TreeNode root){if (root == null){return 0;}return Math.max(depth(root.left),depth(root.right)) + 1;}
3. 最小深度
参考题目介绍:111. 二叉树的最小深度 - 力扣(LeetCode)

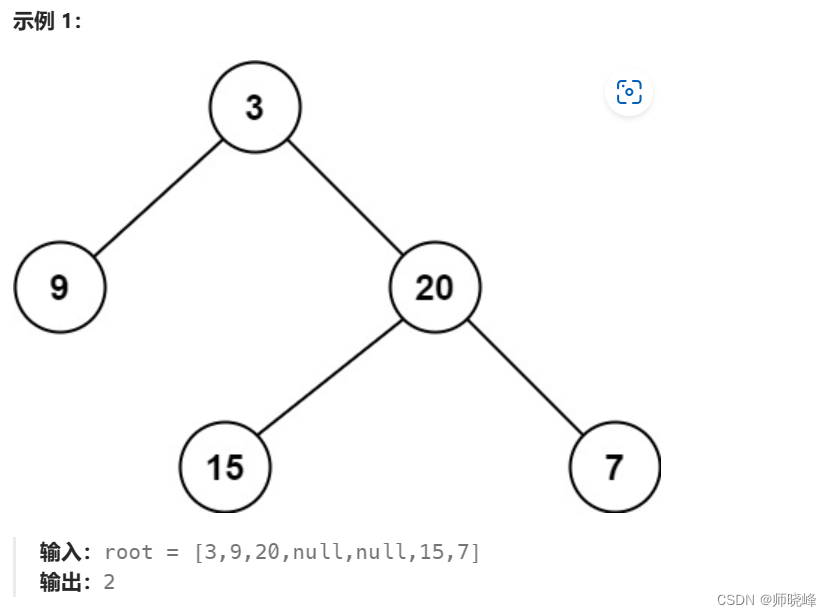
既然有最大深度,可能会有最小深度?这不他就来了,怎么找出最小深度呢?
最小深度:从根节点到最接近叶子节点的最短路径上的节点数量。
看下下面这个特殊例子: 答案是 2 【说明】:叶子节点是指没有子节点的节点。
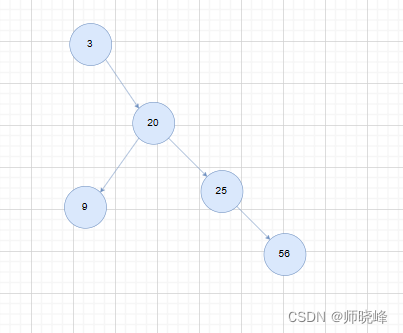
前面两道题涉及到最大深度,这里讲max改成min是不是就可以解决了呢? 不行,你注意看上图:
这里的关键问题是题目中说的:最小深度是从根节点到最近叶子节点的最短路径上的节点数量,也就是说最小深度的一层必须要有叶子节点,不能直接使用。
这里的核心问题仍然是终止条件分析:
- 如果左子树为空,右子树不为空,说明最小深度是1 + 右子树的深度。
- 反之,右子树为空,左子树不为空,最小深度1 + 左子树的深度。
最后如果左右子树都不空,返回左右子树深度最小值+1。
我们看下代码展示😎:
/*** 通过递归计算二叉树的最小** @param root* @return*/public static int minDepth_1(TreeNode root) {if (root == null){return 0;}// 根if (root.left == null && root.right == null){return 1;}// 左int min_depth = Integer.MAX_VALUE;if (root.left != null){min_depth = Math.min(minDepth_1(root.left),min_depth);}// 右if (root.right != null){min_depth = Math.min(minDepth_1(root.right),min_depth);}return min_depth + 1;}
除了递归方式,我们也可以采用层次遍历,只要再遍历时,第一次遇到叶子节点就直接返回,其所在的层次就行,我们可以简单改下层序遍历的方法:
/*** 通过层次遍历来求最大深度** @return*/public static int minDepth_2(TreeNode root) {// 参数检验if (root == null){return 0;}// 创建空间int minDepth = 0;Queue<TreeNode> queue = new LinkedList<>();// 根节点入队,不断循环遍历queue.offer(root);while(!queue.isEmpty()){// 获取队列的长队 这个长度说明这一层有多少个节点int size = queue.size();minDepth++;for(int i = 0; i < size; i++){TreeNode node = queue.poll();if (node.left == null && node.right == null){return minDepth;}if (node.left != null){queue.offer(node.left);}if (node.right != null){queue.offer(node.right);}}}return 0;}
4. N叉树的最大深度
参考题目介绍:559. N 叉树的最大深度 - 力扣(LeetCode)

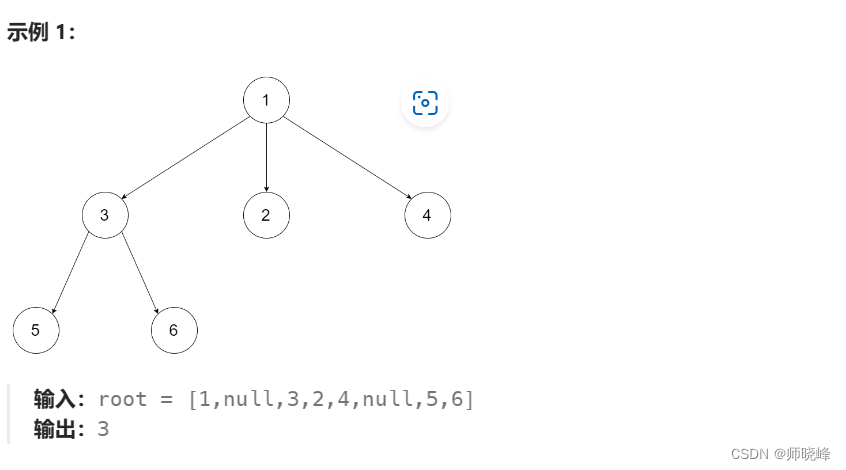
这道题不同的地方是将二叉树换成了N叉树,N叉树的节点较多,我们使用List存储,遍历时采用for即可,我们先看看力扣的N叉树的定义:
class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List<Node> _children) {val = _val;children = _children;}
};
这个题的实现和上个题的最大区别就是在处理子树的问题上面加了个处理List的for循环
代码也很简单🤔:
/*** 递归求N叉树的深度* @param root* @return*/public static int maxDepth_N(NTreeNode root) {if (root == null){return 0;}else if (root.children.isEmpty()){return 1;}else{// 处理子树问题List<Integer> heights = new ArrayList<>();for(NTreeNode item : root.children){heights.add(maxDepth_N(item));}return Collections.max(heights) + 1;}}
当然了,本地还可以使用层序遍历,这个作为拓展感兴趣的话可以试试。
总结
提示:二叉树的深度和高度;N叉树的深度问题;平衡树的判断问题
相关文章:

算法通过村第八关-树(深度优先)白银笔记|深度和高度问题
文章目录 前言1. 最大深度问题2. 判断平衡树3. 最小深度4. N叉树的最大深度总结 前言 提示:我的整个生命,只是一场为了提升社会地位的低俗斗争。--埃莱娜费兰特《失踪的孩子》 这一关我们看一些比较特别的题目,关于二叉树的深度和高度问题。这…...

Redis安装和使用
这里写目录标题 Redis安装和使用一.数据库类型1.关系型数据库2.非关系型数据库3.区别(1)数据存储方式不同(2)扩展方式不同(3)对事务性的支持不同 二.redis简介1.Redis 优点2.哪些数据适合放入缓存中&#x…...

UML基础与应用之面向对象
UML(Unified Modeling Language)是一种用于软件系统建模的标准化语言,它使用图形符号和文本来描述软件系统的结构、行为和交互。在面向对象编程中,UML被广泛应用于软件系统的设计和分析阶段。本文将总结UML基础与应用之面向对象的…...
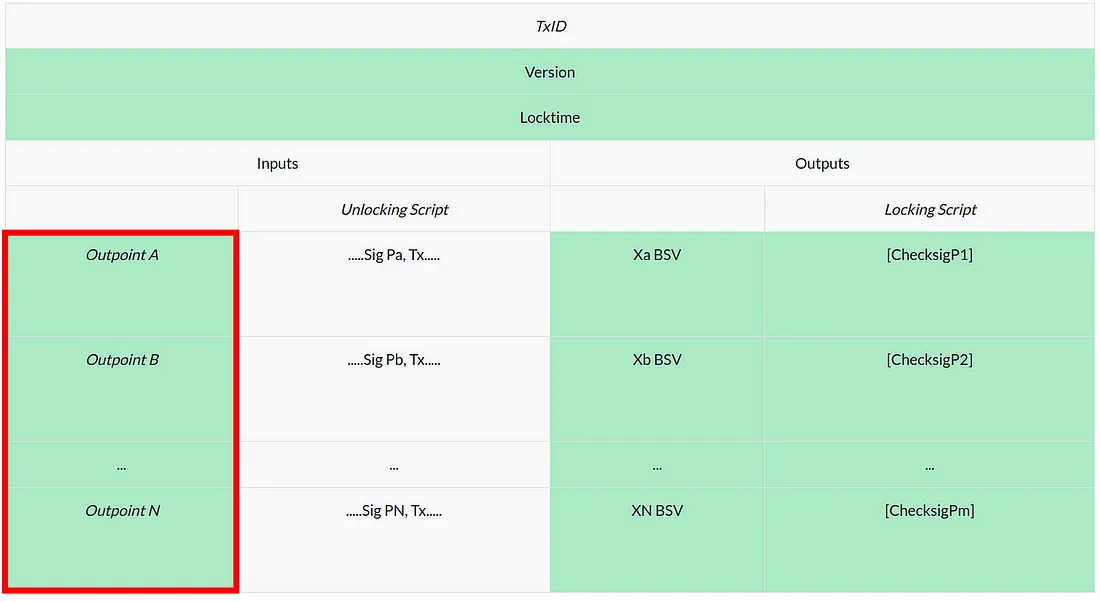
将 Ordinals 与比特币智能合约集成:第 2 部分
在上一篇文章中,我们展示了一种将 Ordinal 与智能合约集成的方法,即将Ordinal和合约放在同一个 UTXO 中。 今天,我们介绍了一种集成它们的替代方案,即它们位于单独的 UTXO 中。 作为展示,我们开发了一个智能合约&…...
)
PCL 法线空间采样(C++详细过程版)
法线空间采样 一、概述二、代码实现三、结果展示1、原始点云2、采样结果一、概述 法线空间采样在PCL里有现成的调用函数,具体算法原理和实现代码见:PCL 法线空间采样。为充分了解法线空间采样算法实现的每一个细节和有待改进的地方,使用C++代码对算法实现过程进行复现。 二…...

论文阅读:AugGAN: Cross Domain Adaptation with GAN-based Data Augmentation
Abstract 基于GAN的图像转换方法存在两个缺陷:保留图像目标和保持图像转换前后的一致性,这导致不能用它生成大量不同域的训练数据。论文提出了一种结构感知(Structure-aware)的图像转换网络(image-to-image translation network)。 Proposed Framework…...

CNC 3D浮雕 Aspire 11.55 Crack
Aspire 提供了功能强大且直观的软件解决方案,用于在 CNC 铣床上创建和切割零件。有用于 2D 设计和计算 2D 刀具路径的工具,例如仿形、型腔加工和钻孔以及 2.5D 刀具路径,包括:V 形雕刻、棱镜雕刻、成型刀具路径、凹槽、 倒角刀具路…...

【Clickhouse2022.02 查询优化】
一、现场场景概述 现场每天每张表入库数据量大约2-4亿条,页面涉及到自定义时间段查询(白天08:00-15:00,夜晚23:00-06:00)与不同时间段(最近一天、一周、一个月和全部)的统计指标查询。 二、主要问题 时间跨度大无查询或查询条件命中数据过多的分页查询场景速度慢 (主要是数据…...
PMP证书在国内已经泛滥了,还有含金量吗?
没有泛滥吧?这个证书现在就是趋向于项目管理人士要去考的呀,也不是考了没用,提升自身个人的能力、找工作方面和晋升加薪方面确实有用呀,不然报名费那么贵,为什么越来越多人考呢? 1、提升自身个人的能力 首…...

SolidJs节点级响应性
前言 随着组件化、响应式、虚拟DOM等技术思想引领着前端开发的潮流,相关的技术框架大行其道,就以目前主流的Vue、React框架来说,它们都基于组件化、响应式、虚拟DOM等技术思想的实现,但是具有不同开发使用方式以及实现原理&#…...
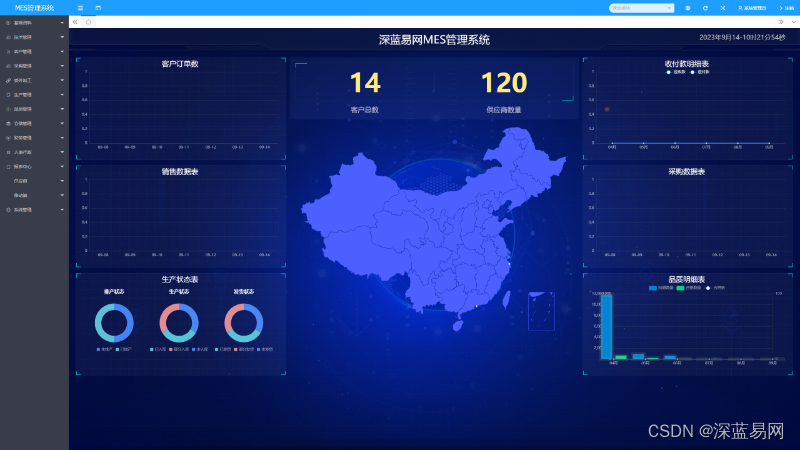
数据采集技术在MES管理系统中的应用及效果
在现代制造业中,MES生产管理系统已成为生产过程中不可或缺的一部分。MES管理系统能够有效地将生产计划、生产执行、质量管理等各个生产环节有机地衔接起来,从而实现生产过程的全面优化。本文将以某车间为例,探讨结合MES系统的数据采集技术的应…...
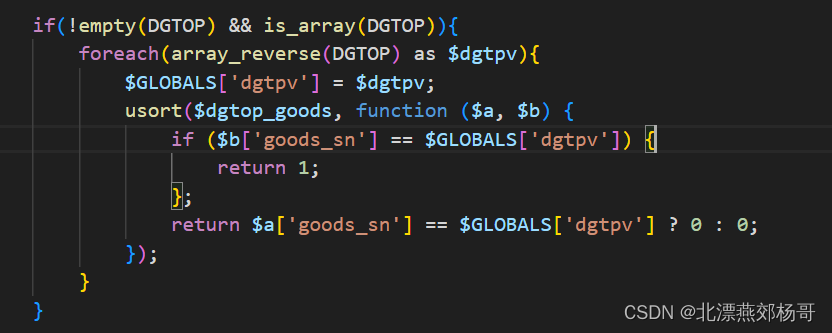
php函数usort使用方法
在 PHP 中,usort() 函数用于对数组进行排序,它允许你使用自定义的比较函数来确定元素的顺序。以下是 usort() 函数的使用方法: usort(array &$array, callable $cmp_function): bool参数说明: $array:要排序的数…...

35.浅谈贪心算法
概述 相信大家或多或少都对贪心算法有所耳闻,今天我们从一个应用场景展开 假设存在下面需要付费的广播台,以及广播台信号可以覆盖的地区。 如何选择最少的广播台,让所有的地区都可以接收到信号? 广播台覆盖地区k1北京、上海、天津…...
【QT基础入门 Demo篇】)
QT时间日期定时器类(1.QDate类)【QT基础入门 Demo篇】
使用时候需要包含头文件 创建一个 QDate 实例 设置 QDate 的日期 获取 QDate 的日期 获取当前是周几 判断 QDate 的有效性 格式化 QDate 的显示字符串 计算 QDate 的差值 QDate显示格式 年月日转换时间戳时间戳转换年月日 QDate相关…...
记一次实战案例
1、目标:inurl:news.php?id URL:https://www.lghk.com/news.php?id5 网站标题:趋时珠宝首饰有限公司 手工基础判断: And用法 and 11: 这个条件始终是为真的, 也就是说, 存在SQL注入的话, 这个and 11的返回结果必定是和正常页…...
Serv-U FTP服务器结合cpolar内网穿透实现共享文件并且外网可远程访问——“cpolar内网穿透”
文章目录 1. 前言2. 本地FTP搭建2.1 Serv-U下载和安装2.2 Serv-U共享网页测试2.3 Cpolar下载和安装 3. 本地FTP发布3.1 Cpolar云端设置3.2 Cpolar本地设置 4. 公网访问测试5. 结语 1. 前言 科技日益发展的今天,移动电子设备似乎成了我们生活的主角,智能…...

EasyWindow - Android 悬浮窗框架
官网 https://github.com/getActivity/EasyWindow 项目介绍 本框架意在解决一些极端需求,如果是普通的 Toast 封装推荐使用 Toaster 集成步骤 如果你的项目 Gradle 配置是在 7.0 以下,需要在 build.gradle 文件中加入 allprojects {repositories {/…...

tp5连接多个数据库
一、如果你的主数据库配置文件都在config.php里 直接在config.php中中定义db2: 控制器中打印一下: <?php namespace app\index\controller; use think\Controller; use think\Db; use think\Request; class Index extends Controller {public fun…...

SAP PO运维(一):系统概览异常处理
打开SAP PIPO Netweaver Administration界面,系统概览下显示异常: 参考SAP note: 2577844 - AS Java Monitoring and Logging parametrization best practice service/protectedwebmethods = SDEFAULT -GetVersionInfo -GetAccessPointList -ListLogFiles -ReadLogFile -Para…...

安全厂商安恒信息加入龙蜥社区,完成 与 Anolis OS 兼容适配
近日,杭州安恒信息技术股份有限公司(以下简称“安恒信息”)签署了 CLA(Contributor License Agreement,贡献者许可协议),正式加入龙蜥社区(OpenAnolis),并成为…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
