算法通过村第九关-二分(中序遍历)黄金笔记|二叉搜索树
文章目录
- 前言
- 1. 有序数组转二叉搜索树
- 2. 寻找连个正序数组的中位数
- 总结
前言
提示:有时候,我感觉自己一辈子活在两个闹钟之间,早上的第一次闹钟,以及5分钟之后的第二次闹钟。 --奥利弗·萨克斯《意识的河流》
每个专题都有简单题,有难的题目。这里就介绍两道有挑战的题,一道是关于二叉搜索树的,一道是从两个数组中寻找中位数的。
1. 有序数组转二叉搜索树
参考题目介绍:108. 将有序数组转换为二叉搜索树 - 力扣(LeetCode)
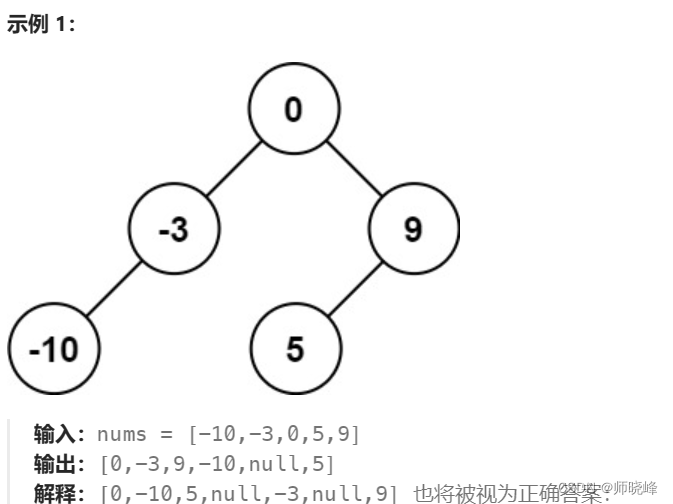
理论上如果要构造二叉搜索树,可以以升序序列中的任意一个元素作为根节点,以该元素左边的升序序列构建左子树,以该元素的右边的升序序列构建右子树,这样得到的树就是一棵二叉搜索树。本体要求高度平衡,一次我们需要选择升序序列的中间元素作为根节点,其本质就是二分查找的过程。
话不多说,看代码😎:
/*** 升序数组转二叉搜索树* @param nums* @return*/public static TreeNode sortedArrayToBST(int[] nums) {return dfs(nums,0,nums.length - 1);}private static TreeNode dfs(int[] nums, int left, int right) {if (left > right){return null;}// 处理节点 总是选择中间位置左边的数字作为根节点int mid = left + ((right - left) >> 1);TreeNode root = new TreeNode(nums[mid]);root.left = dfs(nums,left,mid - 1);root.right = dfs(nums,mid + 1,right);return root;}
除了通过数组构造,是否可以通过一个个插入的方式来实现呢?当然可以。那如果从中间删除一个元素呢?
推荐一下题目:⭐⭐⭐⭐⭐
701. 二叉搜索树中的插入操作 - 力扣(LeetCode)
450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
2. 寻找连个正序数组的中位数
参考题目介绍:4. 寻找两个正序数组的中位数 - 力扣(LeetCode)

对于本题,最值观的思路有一下两种:
- 使用并归的方式,合并两个有序数组,得到一个大的有序数组。大的有序数组中间的元素,即使中位数。这种方式的时间复杂度为O(m + n),空间复杂度为O(m + n)
- 直接找到中位数。由于两个数组的长度已知,因此中位数对应的两个数组的下标之和也是已知的。维护两个指针,初始分别指向两个数组的下标0,0的位置,每次将指针指向较小的指针后移一位,如果指针已经达到数组末尾,只需要移动另一个数组指针,直到到达中位数的位置。这样的方式可以将空间复杂度降低至O(1),但是时间复杂度仍是O(m + n).
如何把时间复杂度降低至O(log(m+n))呢?如果对时间复杂度的要求是log,通常都要考虑二分,快排或者堆三个方面。而对于有序的序列,通常要优先考虑使用二分来解决。
如果要使用二分,核心问题是基于什么规则将数据砍掉一半。而本题是两个序列,所以我们的核心问题是如何从两个序列中分别砍半,图示k = (m + n) >> 1;
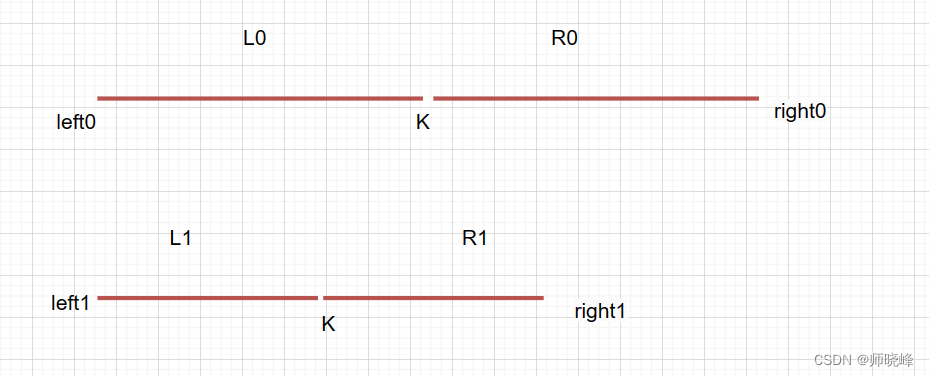
根据中位数的定义,当 m + n是奇数时,中间的两个序列数组的第(m + n) >> 1个元素,当 m + n是偶数时,中间是两个有序数组中的第(m + n) >> 1个元素和第((m + n) >> 1)+ 1的平均值。因此,这道题可以转换为寻找两个有序数组中的第k小的数,其中k为(m + n) >> 1或者((m + n) >> 1)+ 1
假设两个有序数组分别是LA和LB。要找到第k个元素我饿们可以比较LA[k / 2 - 1]和LB[k / 2 -1]。由于LA[k / 2 - 1]和LB[k / 2 -1]的前面分别是LA[k / 2 - 2]和LB[k / 2 -2],即k / 2 - 1个元素,对于LA[k / 2 - 1]和LB[k / 2 -1]中的最小值,最多只会有[k / 2 - 1] + [k / 2 -1] <= k - 2个元素比它小,那么它不就是我们要的第k小的数了。
因此我们可以总结一下:
- 如果LA[k / 2 - 1] < LB[k / 2 -1],则比LA[k / 2 - 1]小的最多有LA的前面k / 2 - 1个数和LB前面k / 2 - 1个数;即比LA[k / 2 - 1]小的数最多只有k - 2个,因此LA[k / 2 - 1]不可能是第k个数,所以LA[0]到LA[k / 2 - 1]也不可能是第k个数,可以全部舍弃掉
- 如果LA[k / 2 - 1] > LB[k / 2 -1],则可以推理排除LB[0]到LB[k / 2 - 1]也不可能是第k个数,可以全部舍弃掉
- 如果LA[k / 2 - 1] > LB[k / 2 -1],则可以归入第一种情况处理。

可以看到,比较LA[k / 2 - 1] > LB[k / 2 -1]之后,可以排除k / 2个不可能是第k小的数,查找范围缩小了一半。同时我们将排除后的数组上继续进行二分查找的话,并且根据我们排除的个数,减少k的值,这是因为我们排除的数都不大于第k小的数。
注意一下边界处理:
- 如果LA[k / 2 - 1] 或者LB[k / 2 -1]越界,那么我们可以以选取对应数组中的最后一个元素。这种情况下,我们必须根据排除数的个数减少k的值,而不是直接将k减去k / 2.
- 如果k = 1 我们只需要返回两数组的首元素的最小值即可。
分析了这么多,怎么写这个代码呢?🤔
/*** 两个有序数组找中间值* @param nums1* @param nums2* @return*/public double findMedianSortedArrays(int[] nums1, int[] nums2) {int length1 = nums1.length,length2 = nums2.length;int totalLength = length1 + length2;if (totalLength % 2 == 1){int midIndex = totalLength >> 1;double median = getKthElement(nums1,nums2,midIndex + 1);return median;}else{int midIndex1 = (totalLength >> 1) - 1;int midIndex2 = (totalLength >> 1);double median = (getKthElement(nums1,nums2,midIndex1 + 1) + getKthElement(nums1,nums2,midIndex2 + 1)) / 2.0;return median;}}private double getKthElement(int[] nums1, int[] nums2, int k) {int length1 = nums1.length,length2 = nums2.length;int index1 = 0, index2 = 0;int kthElement = 0;while(true){// 边界问题if (index1 == length1){return nums2[index2 + k - 1];}if(index2 == length2){return nums1[index1 + k - 1];}if (k == 1){return Math.min(nums1[index1],nums2[index2]);}// 正常情况int half = k >> 1;int newIndex1 = Math.min(index1 + half,length1) - 1;int newIndex2 = Math.min(index2 + half,length2) - 1;int pivot1 = nums1[newIndex1],pivot2 = nums2[newIndex2];if(pivot1 <= pivot2){k -= (newIndex1 - index1 + 1);index1 = newIndex1 + 1;}else{k -= (newIndex2 - index2 + 1);index2 = newIndex2 + 1;}}}
总结
提示:二分进阶;二分搜索;中序遍历;递归算法;分治思想
相关文章:

算法通过村第九关-二分(中序遍历)黄金笔记|二叉搜索树
文章目录 前言1. 有序数组转二叉搜索树2. 寻找连个正序数组的中位数总结 前言 提示:有时候,我感觉自己一辈子活在两个闹钟之间,早上的第一次闹钟,以及5分钟之后的第二次闹钟。 --奥利弗萨克斯《意识的河流》 每个专题都有简单题&a…...

Mock.js之Element-ui搭建首页导航与左侧菜单
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《Spring与Mybatis集成整合》《springMvc使用》 ⛺️ 生活的理想,为了不断更新自己 ! 1、Mock.js的使用 1.1.什么是Mock.js Mock.js是一个模拟数据的生成器,用来帮助前…...
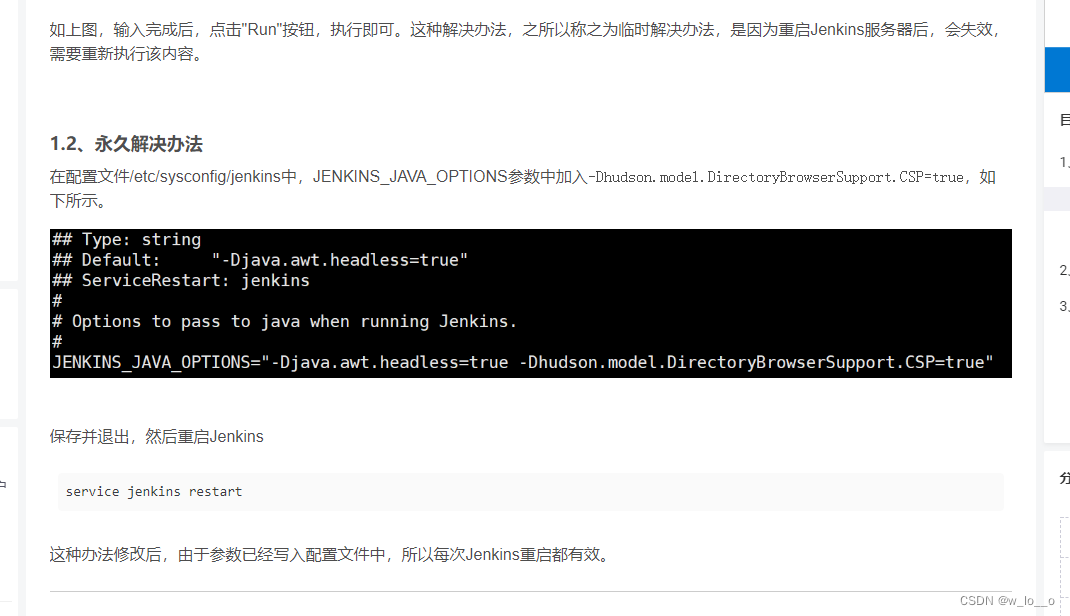
robotframework在Jenkins执行踩坑
1. Groovy Template file [robot_results.groovy] was not found in $JENKINS_HOME/email_template 1.需要在managed files 添加robot_results.groovy。这个名字需要和配置在构建项目里default content一致(Extended E-mail Notification默认设置里Default Content…...
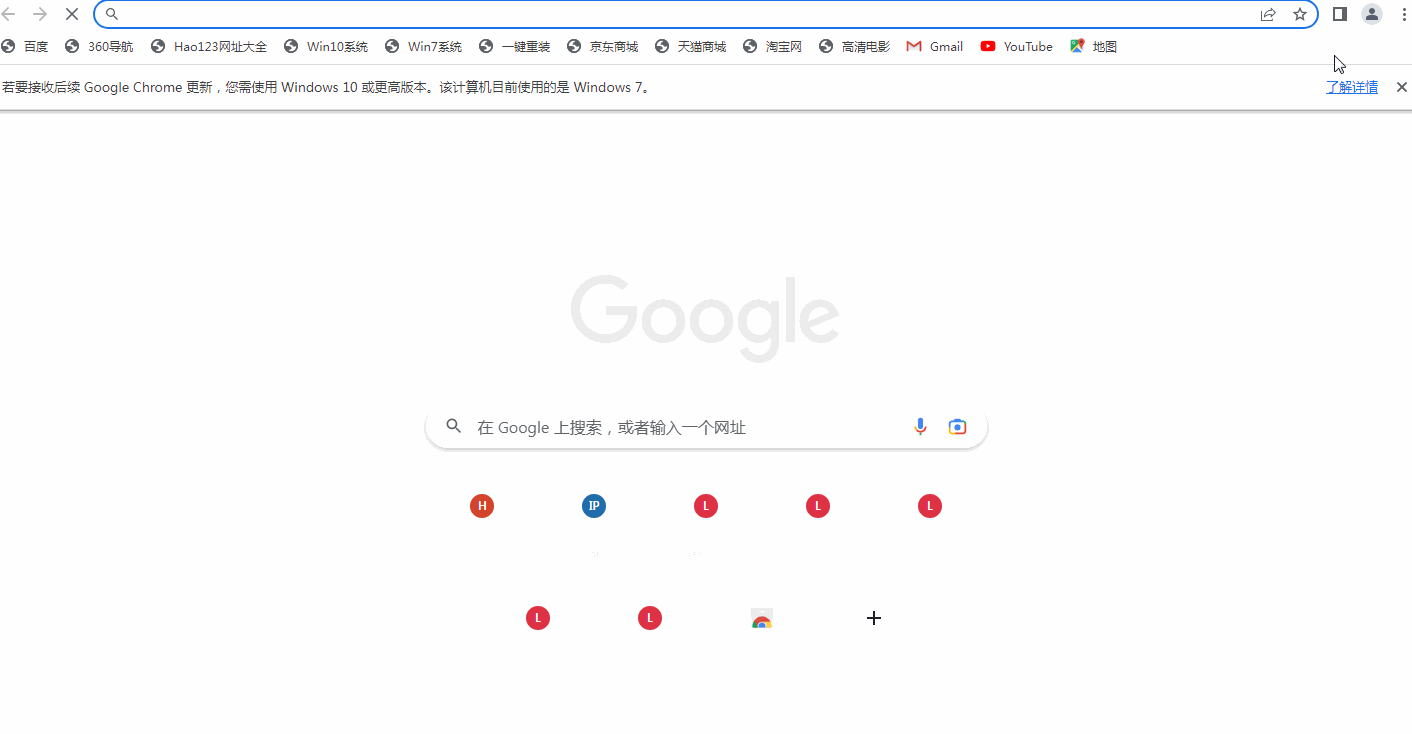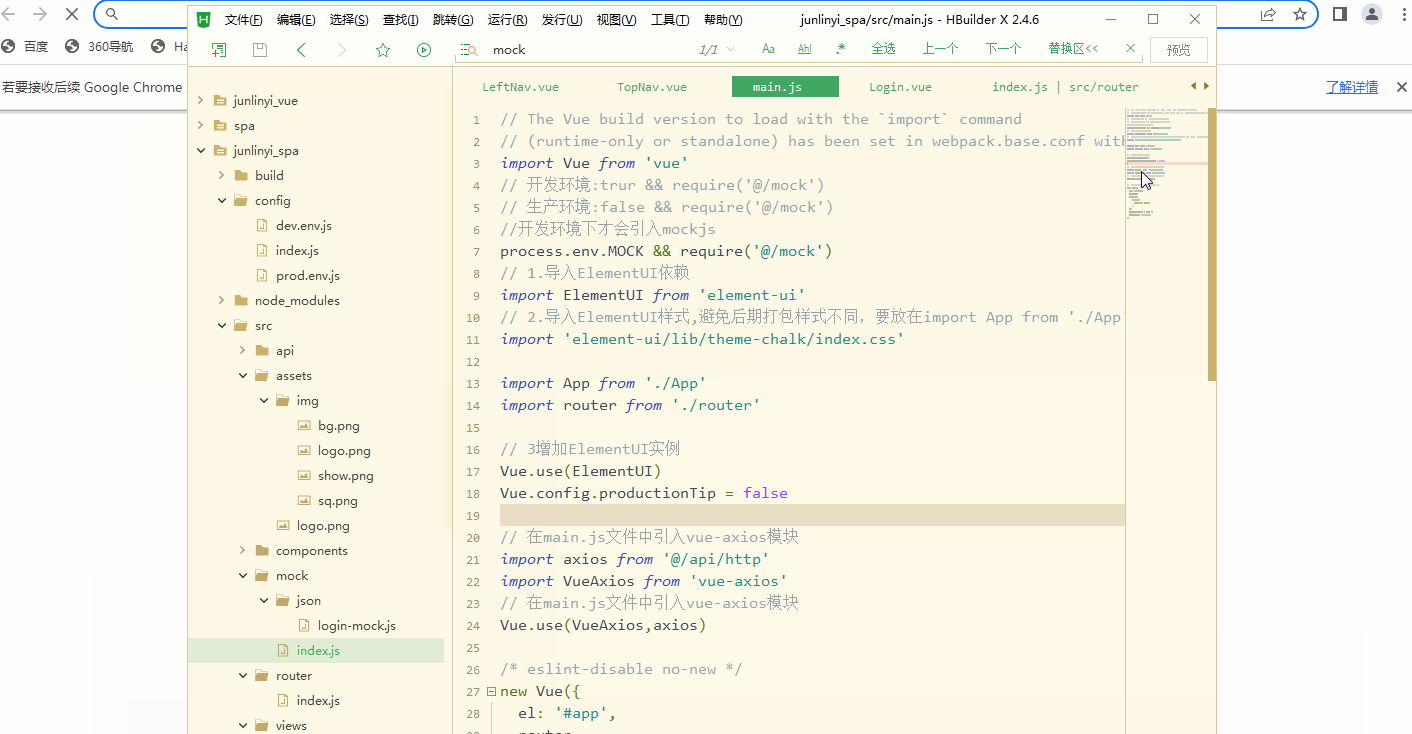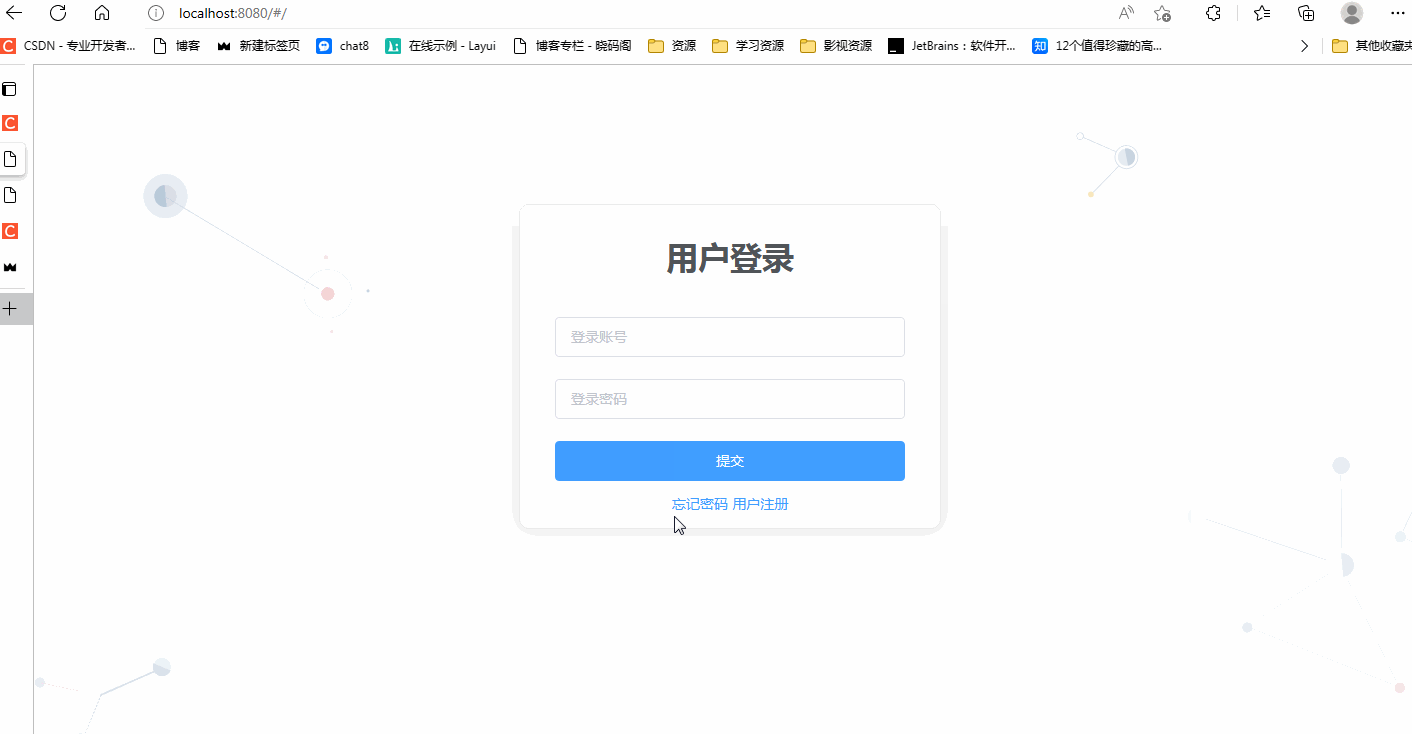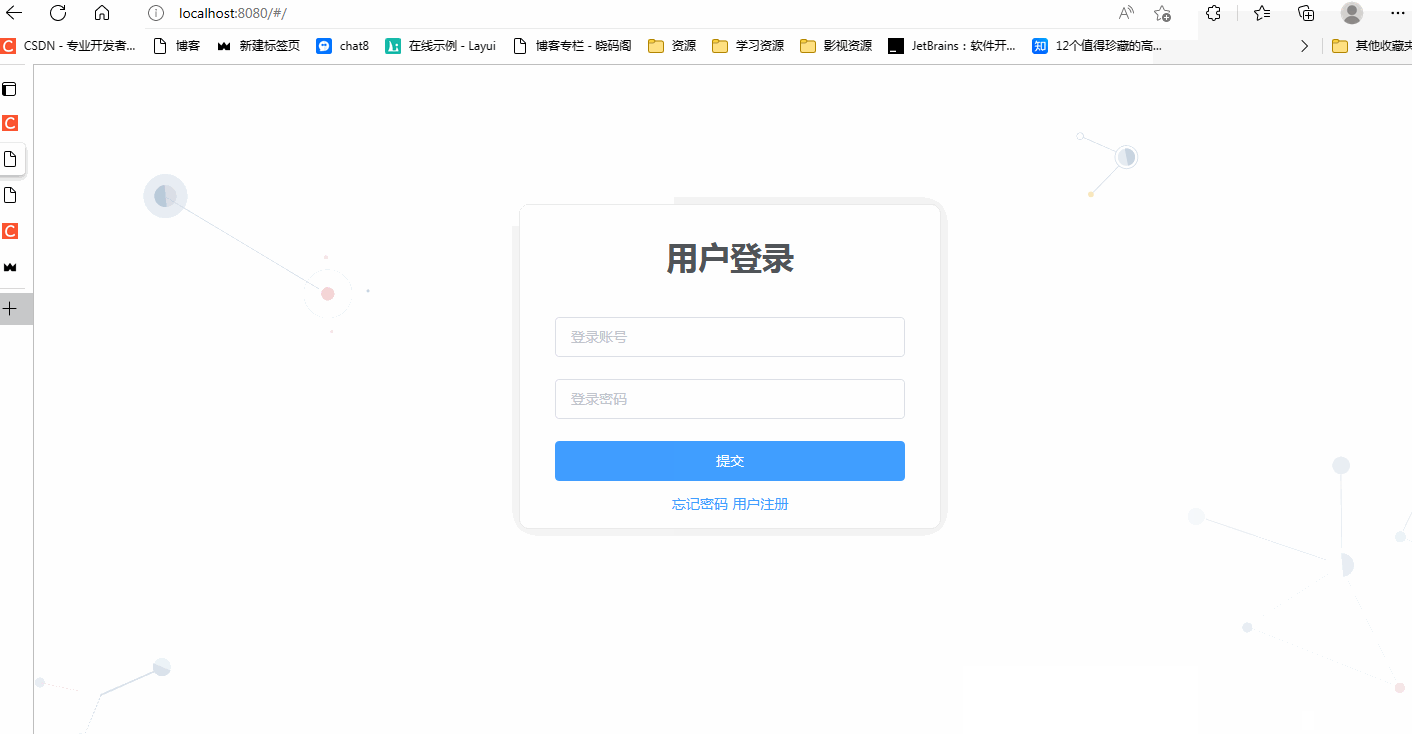
关于ElementUI之首页导航与左侧菜单实现
目录 一.Mock 1.1.什么是Mock.js 1.2.特点 1.3.安装与配置 1.3.1. 安装mock.js 1.3.2.引入mock.js 1.4.mockjs使用 1.4.1.定义测试数据文件 1.4.2.mock拦截Ajax请求 1.4.3.界面代码优化 二.总线 2.1.是什么 2.2.前期准备 2.3.配置组件与路由关系 2.3.1. 配置组件 …...
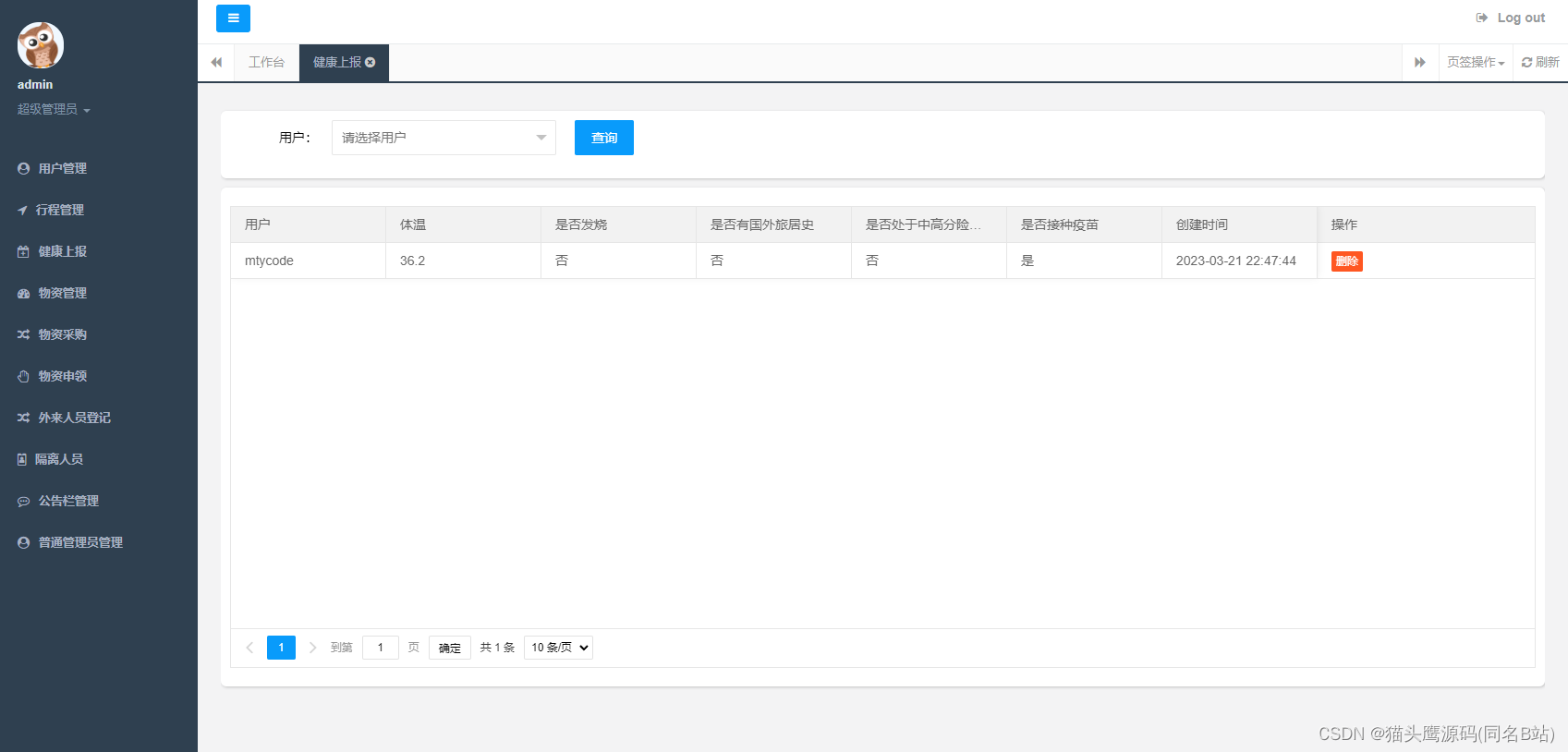
基于springboot小区疫情防控系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

【k8s】YAML语言基础
文章目录 YAML介绍语法支持的数据类型注意事项json与yaml互转 YAML介绍 YAML是一个类似于XML、JSON的标记语言。强调以数据为中心,并不是以标记语言为中心 <heima><age>15</age><address>Beijing</address> </heima>heima:age:…...

AI时代的中国困境: ChatGPT为什么难以复制
如今,几乎所有中国互联网大厂都公布了自己的“类ChatGPT”解决方案,有些还公布了背后的关于AI技术模型的详情。 其中最高调的是百度,其“文心一言”解决方案号称即将接入数十家内容平台和数以百计的媒体、自媒体。腾讯公布的微信 AI 模型“W…...

如何使用Docker安装最新版本的Redis并设置远程访问(含免费可视化工具)
文章目录 安装Docker安装Redisredis.conf文件远程访问Redis免费可视化工具相关链接Docker是一种开源的应用容器引擎,使用Docker可以让我们快速部署应用环境,本文介绍如何使用Docker安装最新版本的Redis。 安装Docker 首先需要安装Docker,具体的安装方法可以参考Docker官方文…...
怒刷LeetCode的第8天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:双指针和排序 编辑第二题 题目来源 题目内容 解决方法 方法一:双指针 方法二:递归 方法三:快慢指针 方法四:栈 第三题 题目来源 题目内容 解决方法…...

Vue Hooks 让Vue开发更简单与高效
Vue Hooks 让Vue开发更简单与高效 介绍 Vue Hooks 是一个基于 Vue.js 的插件,它提供了一种新的方式来编写 Vue 组件,使得开发更加简单和高效。它借鉴了 React Hooks 的概念,通过使用 Hooks,我们可以在不编写类组件的情况下&…...

Go编程规范
文章目录 注释转义符定义变量方法一:指定变量类型,声明后若不赋值,使用默认值方法二:根据值自行判定变量类型(类型推导)方法三:省略var, 注意:左侧的变量不应该是已经声明过的,否则会导致编译错误[推荐]全局…...
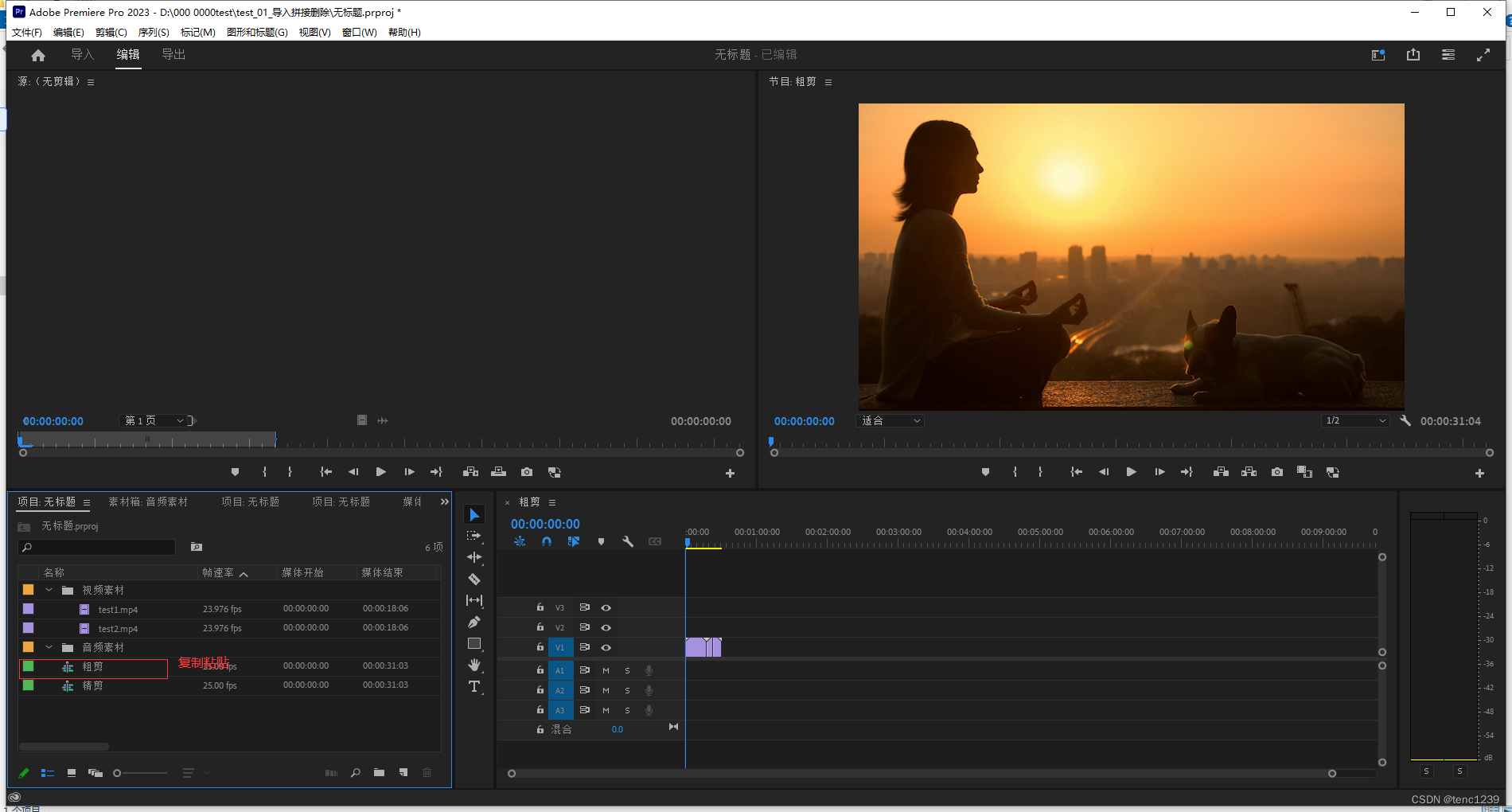
premiere 新建 视频导入 视频拼接 视频截取 多余视频删除
1 新建项目 文件 -> 新建 -> 项目 2 导入 2.1 方法一 直接从本地 将 文件拖入对应的文件夹 2.2 方法二 鼠标右键在指定素材文件夹, 选择导入 选择对应本地文件夹对应素材 3 预设 -> 粗剪 -> 在指定模块处 创建序列预设 3.1 指定模块处 鼠标右键 -> 新建项目…...

笔记01:第一行Python
NameError 名字不含特殊符号(只能是英文、数字、下划线、中文等)名字区分大小写名字先定义后使用 SyntaxError 不符合Python语法书写规范除了语法成分中的保留拼写错误输出中文符号if、for、def等语句末尾忘记冒号 IdentationError 缩进错误&#x…...

资产连接支持会话分屏,新增Passkey用户认证方式,支持查看在线用户信息,JumpServer堡垒机v3.7.0发布
2023年9月25日,JumpServer开源堡垒机正式发布v3.7.0版本。在这一版本中,在用户管理层面,为了提高使用JumpServer操作资产的效率,JumpServer支持对会话进行分屏操作,用户可以在一个浏览器页面打开多个会话,方…...
分包优化和游客模式)
uniapp项目实践总结(二十二)分包优化和游客模式
导语:这篇主要介绍应用分包和游客模式相关的内容。 目录 应用分包游客模式 应用分包 微信对于小程序的打包压缩后的代码体积是有限制的,网页和 APP 也可以适用分包功能,因此需要进行分包添加以及分包优化。 分包添加 在pages.json文件中…...
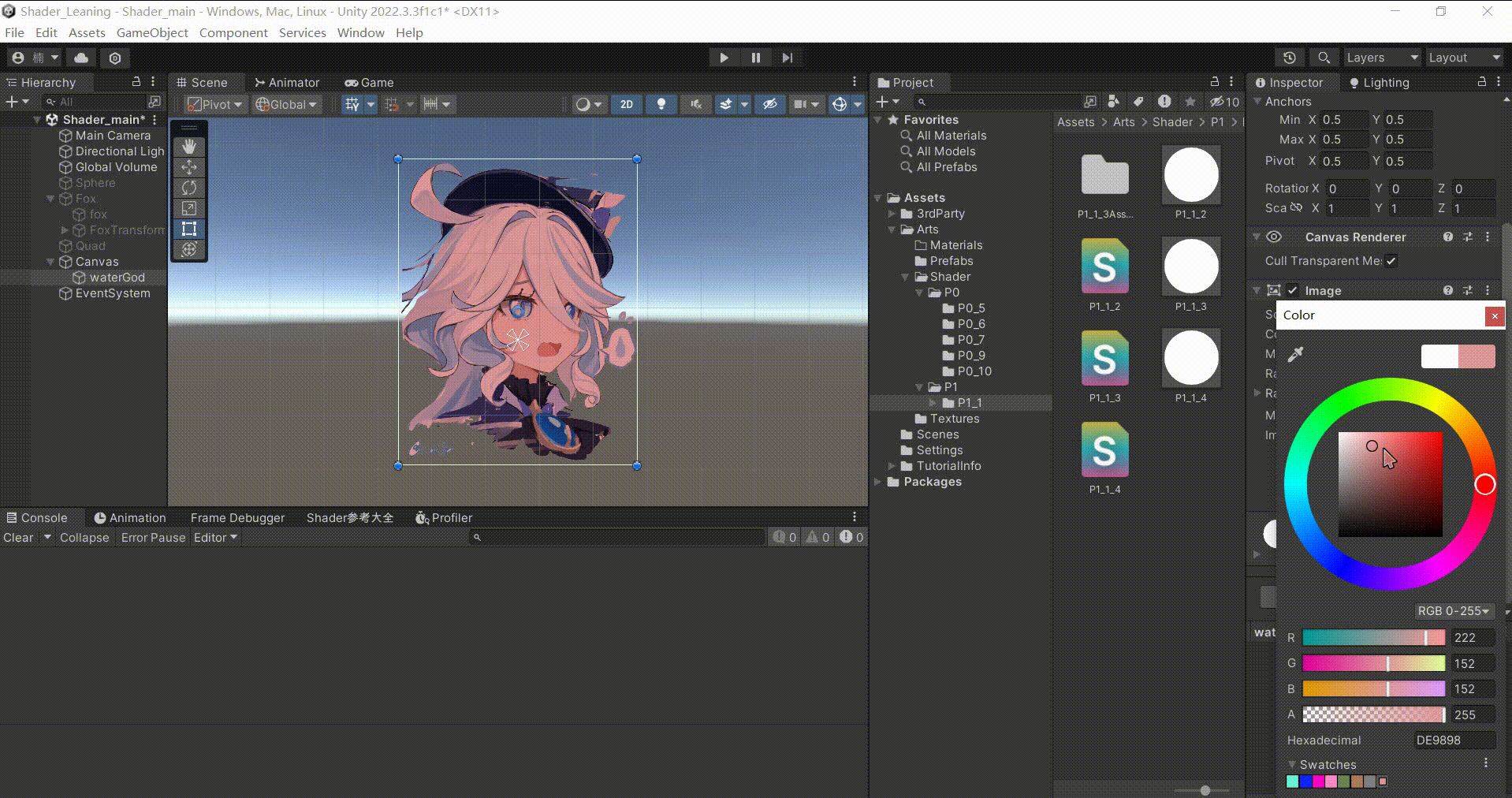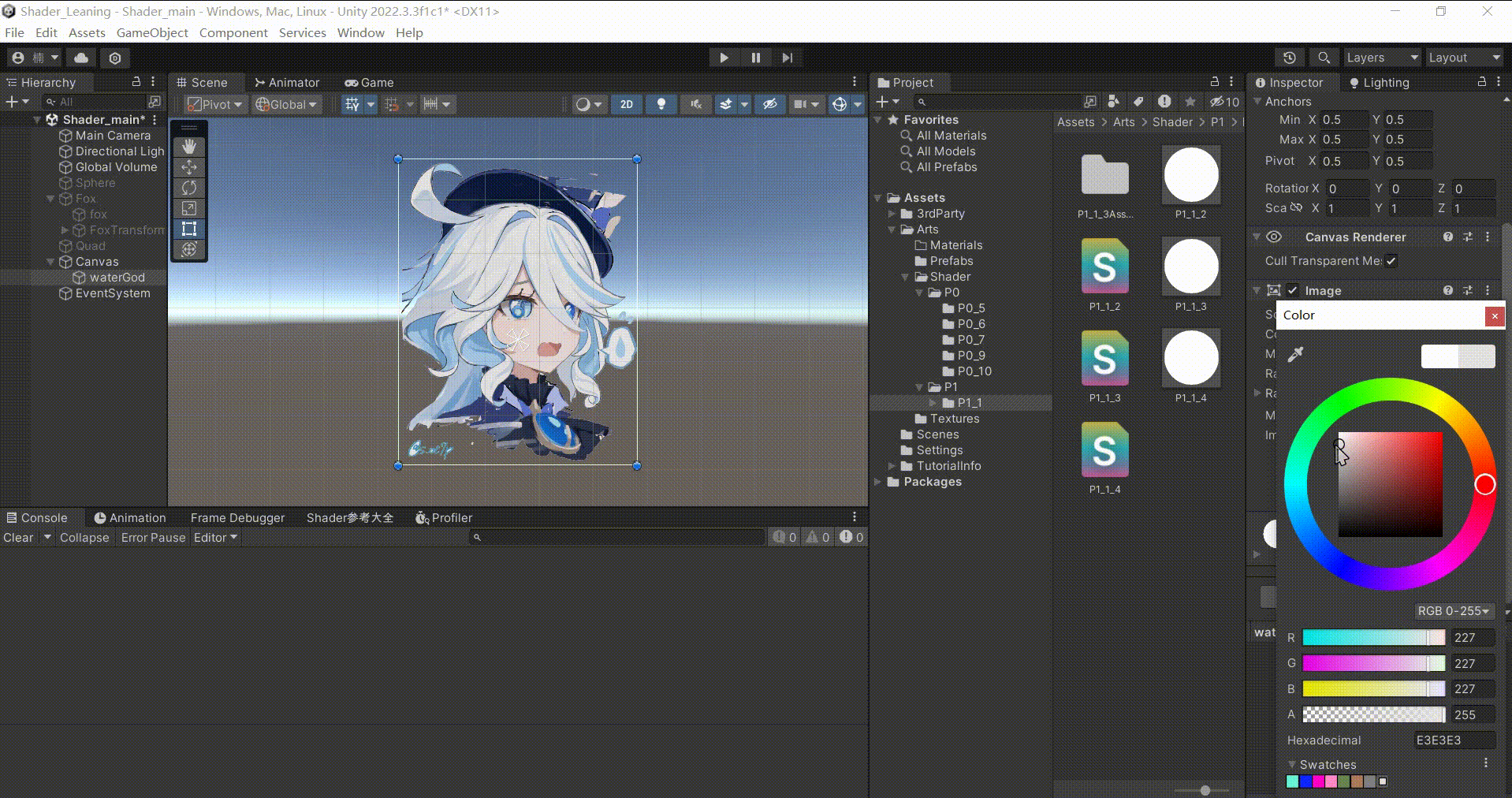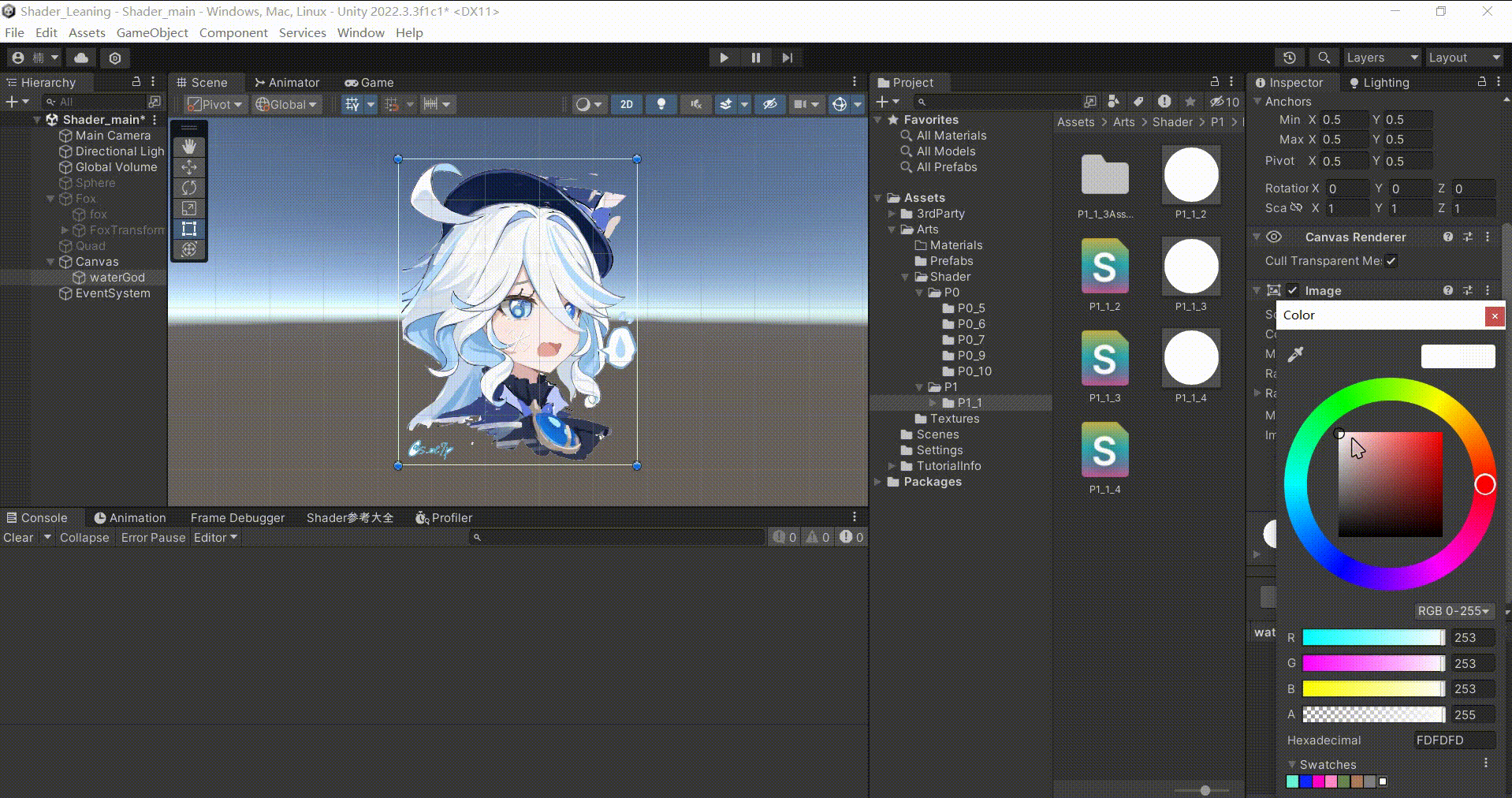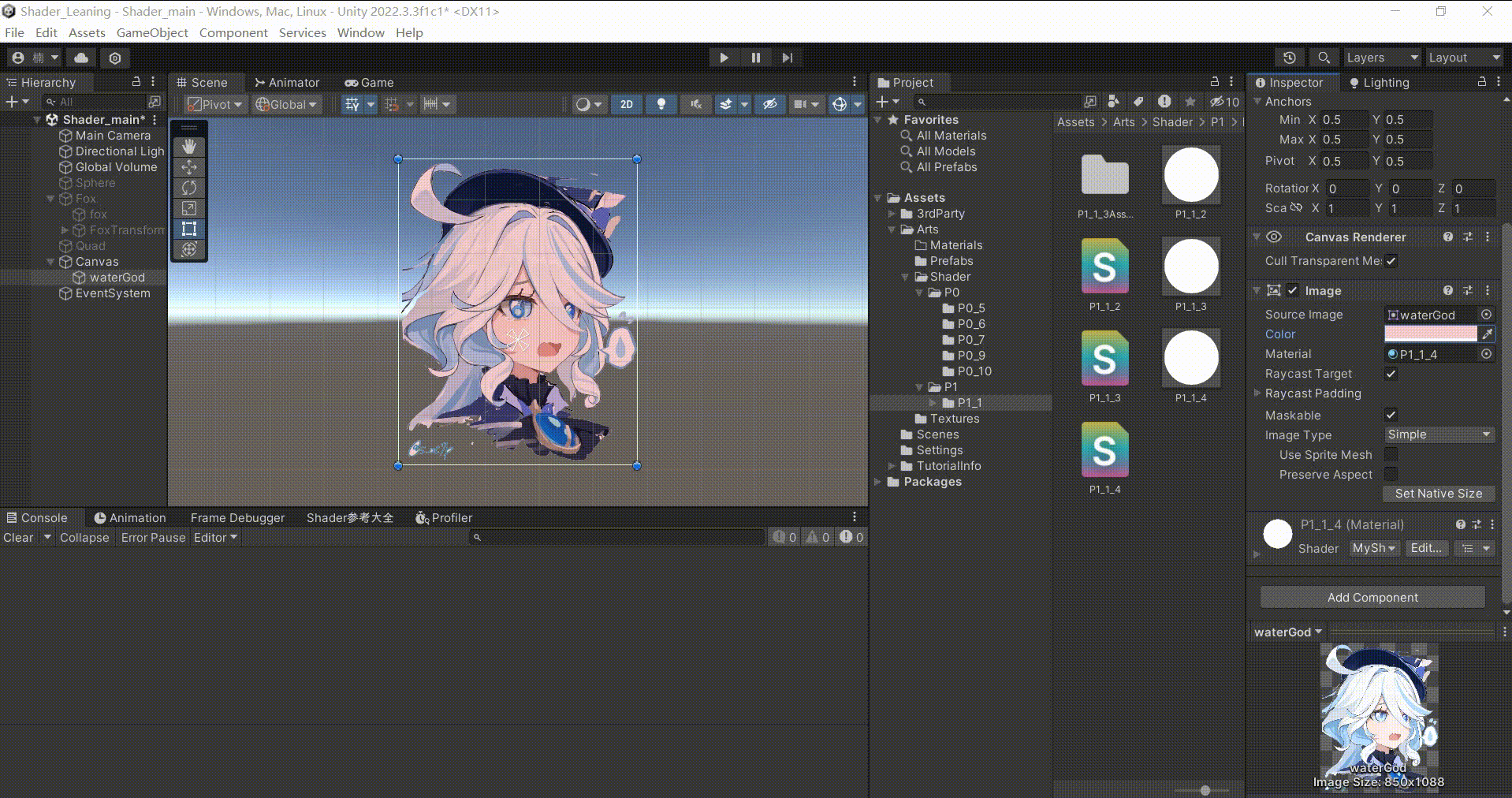
Unity中UI组件对Shader调色
文章目录 前言一、原理在Shader中直接暴露的Color属性,不会与UI的Image组件中的Color形成属性绑定。因为UI的Image组件中更改的颜色是顶点颜色,如果需要在修改组件中的颜色时,使Shader中的颜色也同时改变。那么就需要在应用程序阶段传入到顶点…...

PhpStorm 2023年下载、安装教程和好用插件,保姆级教程
PhpStorm 2023年下载、安装教程和好用插件,保姆级教程 文章目录 PhpStorm 2023年下载、安装教程和好用插件,保姆级教程前言一、安装PhpStorm二、好用的插件简体中文包Chinese(Simplified)Language Pack 三、卸载插件CTRLN 查找类CTRLSHIFTN 全局搜索文件…...
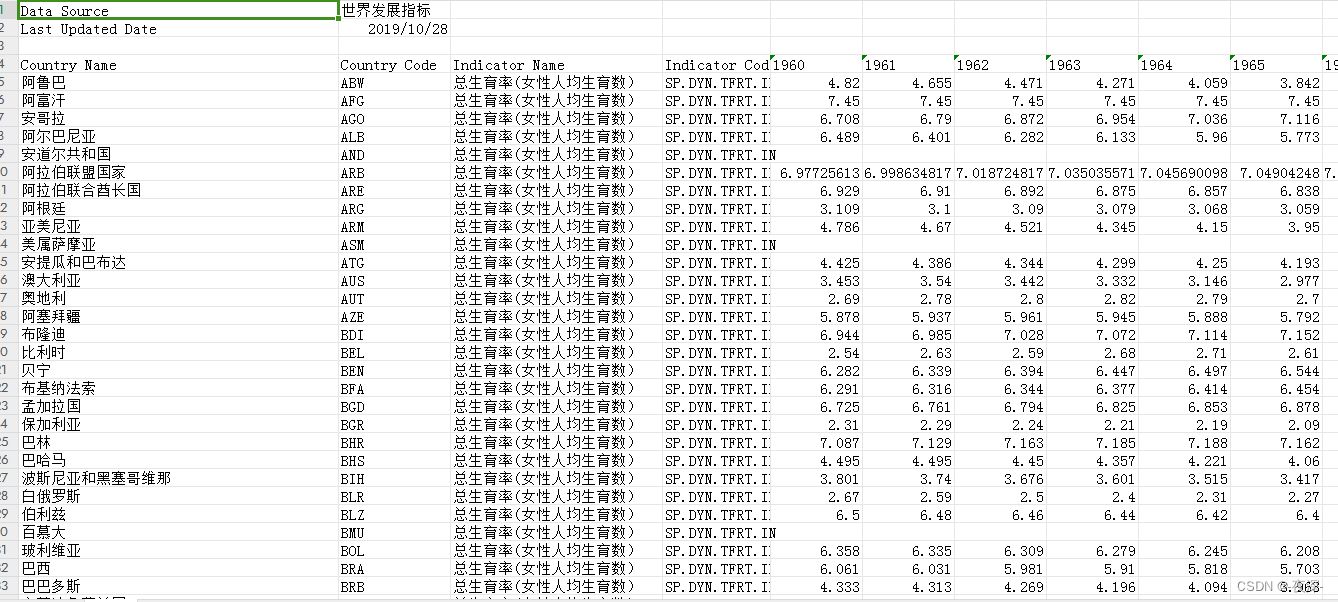
1960-2017年世界各国总和生育率数据
1960-2017年世界各国总和生育率数据 1、时间:1960-2017年 2、指标:生育率 3、范围:全球各国 4、来源:世界银行 5、指标解释: 总生育率表示假设妇女度过整个生育期并按照当期的年龄别生育率生育孩子所生育的孩子数…...

java.math.BigDecimal is not a supported Java type
文章目录 问题描述:结果:原因:Thrif支持的数据类型解决:规范 问题描述: 前端查询后端的pcs总数字段,此字段需要从mydsql的db中获取。PCS字段类型为decimal(26,6),于是打算在response中使用 Big…...

Unity之Hololens开发如何实现UI交互
一.前言 什么是Hololens? Hololens是由微软开发的一款混合现实头戴式设备,它将虚拟内容与现实世界相结合,为用户提供了沉浸式的AR体验。Hololens通过内置的传感器和摄像头,能够感知用户的环境,并在用户的视野中显示虚拟对象。这使得用户可以与虚拟内容进行互动,将数字信…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
