LeetCode 面试题 05.04. 下一个数
文章目录
- 一、题目
- 二、Java 题解
- 2.1 求大数:
- 2.2 求小数:
一、题目
下一个数。给定一个正整数,找出与其二进制表达式中1的个数相同且大小最接近的那两个数(一个略大,一个略小)。
示例1:
输入: num = 2(或者0b10)
输出: [4, 1] 或者([0b100, 0b1])
示例2:
输入: num = 1
输出: [2, -1]
提示:
num的范围在[1, 2147483647]之间;- 如果找不到前一个或者后一个满足条件的正数,那么输出 -1。
点击此处跳转题目。
二、Java 题解
看了一些题解后,分享一下我个人认为自己的较为简单易懂的代码。
求大数和小数可以看做是进/退位运算,因此从右向左对二进制进行遍历,使用 ones 记录出现过 1 的次数。
2.1 求大数:
求大数即进位,从左向右用指针 i(从 0 开始计数)对 num 进行判断,遇到 1 后第一次遇到 0 即停止。此时 i 指向 0,右方是连续的 1 串。将右方的连续 1 串进位(即 i 指向的 0 变为 1),之后重组剩余的 ones - 1 个 1(向右靠拢),得到最小的大数:
⟵ i 0 1 0 ⏞ i = 5 1 1 1 ⏞ o n e s = 3 0 0 ⇓ + 1 0 0 ⏞ i − o n e s 个 0 1 1 ‾ 0 0 0 0 0 ⇓ + 1 1 ⏞ o n e s − 1 个 0 1 1 0 0 0 1 ‾ 1 ‾ \begin{array}{l} \hspace{10em} \longleftarrow^{\normalsize{i}}\\ 0 \hspace{1em} 1 \hspace{0.5em} \overbrace{0}^{i=5} \hspace{0.5em} \overbrace{1 \hspace{1em} 1 \hspace{1em} 1 }^{ones=3} \hspace{1em} 0 \hspace{1em} 0 \\\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\Downarrow \scriptsize {\hspace{1em}+\hspace{1em}1\overbrace{0\hspace{1em}0}^{i-ones个}} \\\\ 0 \hspace{1em} 1 \hspace{1em} \underline{\bold{1}} \hspace{0.9em} 0 \hspace{1em} 0 \hspace{1em} 0 \hspace{1em} 0 \hspace{1em} 0 \\\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\Downarrow \scriptsize {\hspace{1em}+\overbrace{1\hspace{1em}1}^{ones-1个}}\\\\ 0 \hspace{1em} 1 \hspace{1em} 1 \hspace{1em} 0 \hspace{1em} 0 \hspace{1em} 0 \hspace{1em} \underline{\bold{1}} \hspace{0.9em} \underline{\bold{1}} \end{array} ⟵i010 i=5111 ones=300⇓+100 i−ones个01100000⇓+11 ones−1个01100011
2.2 求小数:
求小数即退位,从左向右用指针 i 对 num 进行判断,遇到 0 后第一次遇到 1 即停止。此时 i 指向 1,右方是连续的 0 串。i 位退位(即 i 指向的 1 变为 0),之后重组剩余的 ones - 1 个 1(向左靠拢),得到最大的小数:
⟵ i 1 1 ⏞ i = 6 0 0 1 1 1 1 ⏞ o n e s = 4 ⇓ + 1 1 1 0 1 ‾ 0 0 0 0 ⇓ − 1 0 0 0 0 ⏞ o n e s 个 1 1 0 0 ‾ 0 0 0 0 ⇓ − 1 0 ⏞ i − o n e s − 1 个 1 0 ‾ 1 ‾ 1 ‾ 1 ‾ 1 ‾ 1 ‾ ⏞ o n e s + 1 个 0 ⏟ i 个 \begin{array}{l} \hspace{10em} \longleftarrow^{\normalsize{i}}\\ 1 \hspace{0.5em} \overbrace{1}^{i=6} \hspace{0.5em} 0 \hspace{1em} 0 \hspace{1em} \overbrace{1 \hspace{1em} 1 \hspace{1em} 1 \hspace{1em} 1}^{ones=4} \\\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\Downarrow \scriptsize {\hspace{1em}+\hspace{1em}1} \\\\ 1 \hspace{1em} 1 \hspace{1em} 0 \hspace{1em} \underline{\bold{1}} \hspace{0.9em} 0 \hspace{1em} 0 \hspace{1em} 0 \hspace{1em} 0 \\\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\Downarrow \scriptsize {\hspace{1em}-1\hspace{1em}\overbrace{0\hspace{1em}0\hspace{1em}0\hspace{1em}0}^{ones个}}\\\\ 1 \hspace{1em} 1 \hspace{1em} 0 \hspace{1em} \underline{\bold{0}} \hspace{0.9em} 0 \hspace{1em} 0 \hspace{1em} 0 \hspace{1em} 0 \\\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\Downarrow \scriptsize {\hspace{1em}-1\hspace{0.4em}\overbrace{0}^{i-ones-1个}}\\\\ 1 \hspace{1em} \underline{\bold{0}} \hspace{0.8em} \underbrace{\overbrace{\underline{\bold{1}} \hspace{0.8em} \underline{\bold{1}} \hspace{0.85em} \underline{\bold{1}} \hspace{0.8em} \underline{\bold{1}} \hspace{0.85em} \underline{\bold{1}}}^{ones+1个} \hspace{0.85em} 0}_{i个} \\\\ \end{array} ⟵i11 i=6001111 ones=4⇓+111010000⇓−10000 ones个11000000⇓−10 i−ones−1个10i个 11111 ones+1个0
class Solution {public int[] findClosedNumbers(int num) {int[] ans = new int[] { -1, -1 };// 求大数int ones = 0;for (int i = 0; i < 31; i++) { // i < 31 表示不考虑符号位if ((num & (1 << i)) != 0) ones++; // 遇到 1 更新 onesif ((num & (1 << i)) == 0 && ones > 0) { // 遇到 1 后的第一个 0ans[0] = num + (1 << (i - ones)) + (1 << (ones - 1)) - 1;break;}}// 求小数ones = 0;for (int i = 0; i < 31; i++) {if ((num & (1 << i)) == 0) continue; // 忽略 0// 以下为遇到 1 的情况if (i > ones) { // i 比 ones 大,表示前面遇到了 0ans[1] = num - (1 << ones) - (1 << (i - ones - 1)) + 1;break;}ones++; // 更新 ones}return ans;}
}
- 时间:0 ms,击败 100.00% 使用 Java 的用户
- 内存:37.83 MB,击败 91.57% 使用 Java 的用户
相关文章:

LeetCode 面试题 05.04. 下一个数
文章目录 一、题目二、Java 题解2.1 求大数:2.2 求小数: 一、题目 下一个数。给定一个正整数,找出与其二进制表达式中1的个数相同且大小最接近的那两个数(一个略大,一个略小)。 示例1: 输入: n…...

SDXL prompt 笔记
模型 模型有两个,分别是 stable-diffusion-xl-base-1.0、stable-diffusion-xl-refiner-1.0。 base 模型是用来做文生图,refiner 模型是用来做图生图的。 SDXL 模型之 base、refiner 和 VAE_云水木石的博客-CSDN博客 分辨率 默认是1024*1024…...

使用Redis管道进行查询接口性能优化
一、引入 在我们的正常项目开发过程中,我们会通过Redis缓存数据,来帮我们进行异步任务,分担外部的请求压力 但是Redis缓存也有一定的限制,因为我们在向请求过来时,Redis客户端都要向服务端发送一次请求,相应…...

初学vue.js
准备Vue.js环境 ① 下载环境: javaScript语言的程序包:外部js文件 对于Vue来说,导入Vue的外部js文件就能够使用Vue框架了。 Vue框架的js文件获取: 官网提供的下载地址:https://cdn.jsdelivr.net/npm/vue/dist/vue.js ②导入环境…...

React的thunk中间件
Thunk 是一种中间件,它可以在 Redux 中处理异步操作。Thunk 中间件允许你在 action 中返回一个函数,而不仅仅是一个普通的 action 对象。这个返回的函数可以接收 dispatch 和 getState 作为参数,并且可以在函数内部进行异步操作。当使用 Thun…...

数组初学者向导:使用Python从零开始制作经典战舰游戏
引言 战舰游戏,一个广受欢迎的经典游戏,为玩家提供了策略与猜测的完美结合。这个游戏的核心思想是通过猜测敌方船只的位置并尝试击沉它们来赢得比赛。在这篇文章中,我们将使用Python语言和数组来构建这款游戏,让你更加了解数组的…...

【STM32】IAP升级 预备知识
IAP(In Application Programming)简介 Flash够大的情况下,上电后的程序通过修改 MSP 的方式,可以在一块Flash上存在多个功能差异的程序。 IAP是为了在执行正常功能前,为了升级功能,提前运行的一段程序。这…...
asp.net网站的建立及运行
点击创建新项目 在输入框中输入asp.net,并选择图中的 点击下一步 点击创建 然后,右键,添加,新建项 选择web窗体 点击添加 点击视图,工具箱 选择一个label,记住这个id 空白处右键,查看代码 添…...
怎么把webm转换成mp4?
怎么把webm转换成mp4?与MP4这位视频格式大哥相比,Webm这种视频格式还有很多小伙伴对它不太熟悉,因为大家平时也是偶尔才能接触到,属于不常用的视频格式。Webm是一种开放、免费的媒体文件格式,尽管如今它的应用范围比以…...

RabbitMQ 消息应答
每日一句 物是人非事事休,欲语泪先流。 概述 为了保证消息在发送过程中不丢失,RabbitMQ引入了消息应答机制, 消费者在接收到消息并且处理该消息后,告诉RabbitMQ它已经处理了,RabbitMQ可以把消息删除了。 自动应答 消息发送后立即被认为已经传送成功,这种模式需要在…...
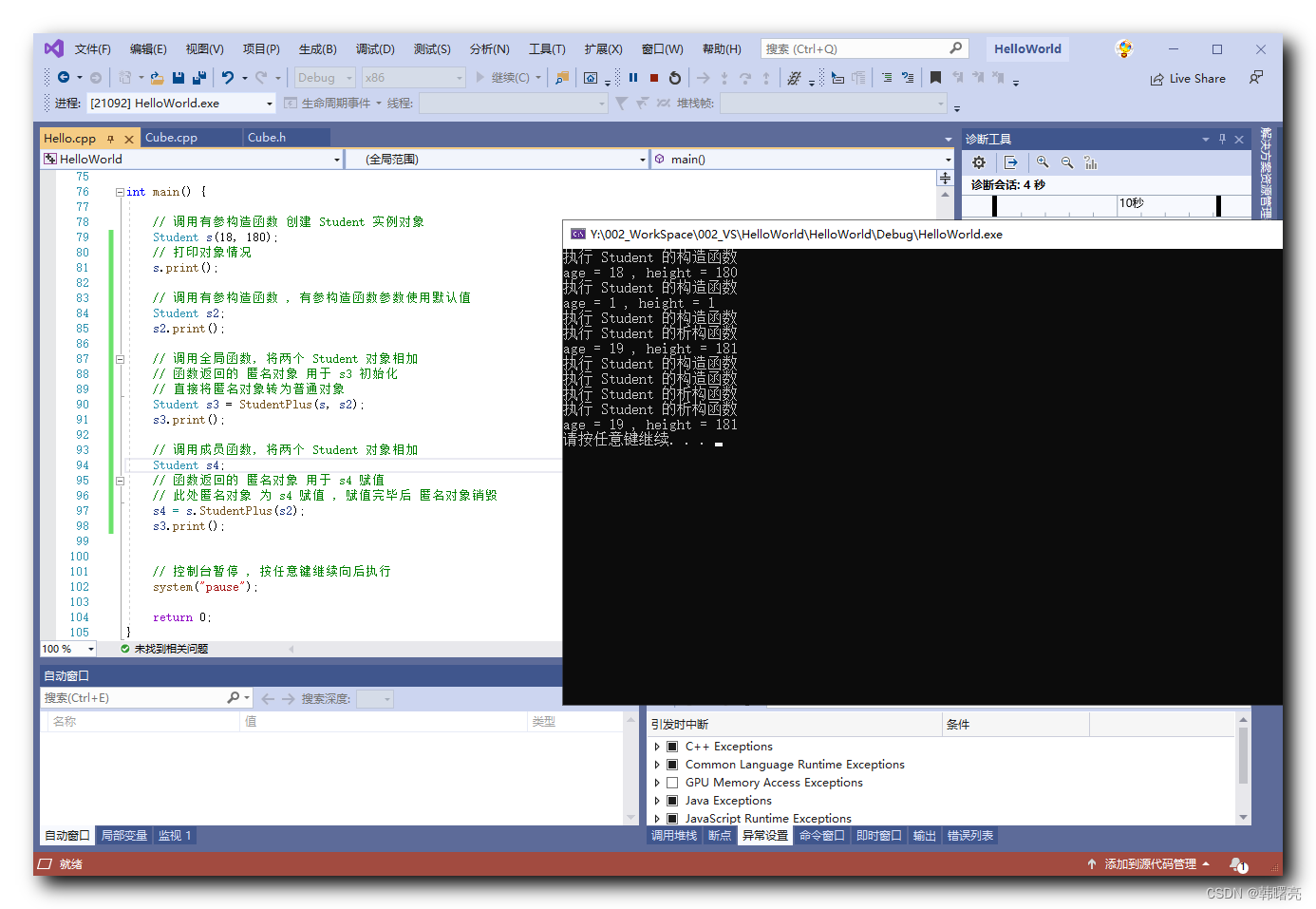
【C++】C++ 类中的 this 指针用法 ③ ( 全局函数 与 成员函数 相互转化 | 有参构造函数设置默认参数值 | 返回匿名对象与返回引用 )
文章目录 一、全局函数 与 成员函数 相互转化1、成员函数转为全局函数 - 多了一个参数2、全局函数转为成员函数 - 通过 this 指针隐藏操作数 二、有参构造函数设置默认参数值三、返回匿名对象与返回引用四、完整代码示例 一、全局函数 与 成员函数 相互转化 1、成员函数转为全局…...

游戏遇到的问题
天涯明月刀 就是天刀的假全屏,很多天刀玩家可能玩其他游戏比较少或者对电脑了解不多,不在意帧数,但是肯定还是有一部分玩家发现了这个问题,就是“我使命召唤12都能跑到60帧的机器跑个破天刀40帧甚至30帧?”问题何在呢࿱…...

高性能系统的性能优化技巧:从专家的经验中学习 | 开源日报 No.40
binhnguyennus/awesome-scalability Stars: 48.3k License: MIT 这个项目是一个阅读列表,用于说明可扩展、可靠和高性能大规模系统的模式。该项目通过知名工程师的文章和可信参考资料来解释概念,并从为数以百万计甚至十亿用户提供服务的经过实战验证的系…...

Linux系统编程——进程间通信的学习
学习参考博文: 进程间的五种通信方式介绍Linux 信号介绍 Linux系统编程学习相关博文 Linux系统编程——文件编程的学习Linux系统编程——进程的学习Linux系统编程——线程的学习Linux系统编程——网络编程的学习 Linux系统编程——进程间通信的学习 一、概述1. 无…...

人工智能AI 全栈体系(六)
第一章 神经网络是如何实现的 这些年神经网络的发展越来越复杂,应用领域越来越广,性能也越来越好,但是训练方法还是依靠 BP 算法。也有一些对 BP 算法的改进算法,但是大体思路基本是一样的,只是对 BP 算法个别地方的一…...
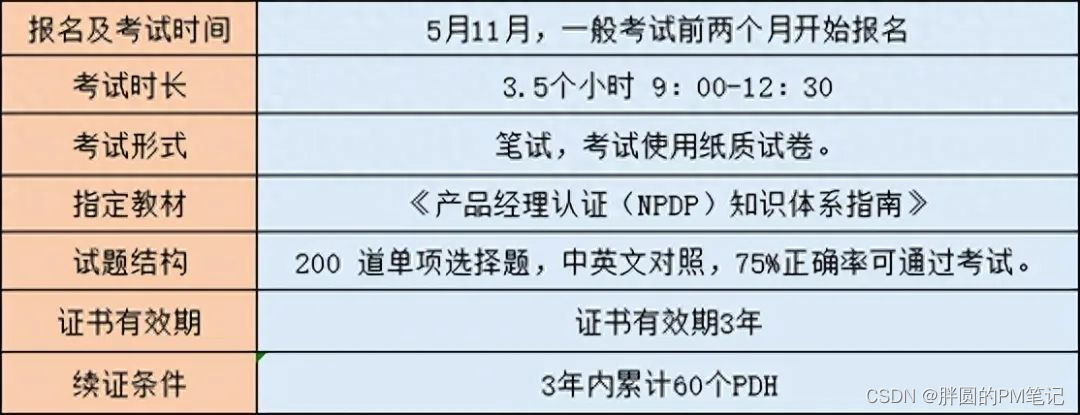
NPDP是什么?考了有用吗?
1)NPDP是什么? NPDP,全称为New Product Development Professional,即新产品开发专业人员。NPDP认证是由世界产品开发协会(PDMA)推出的一项专业认证。它旨在评估和认可个人在新产品开发领域的专业知识和技能…...

关于安卓SVGA浅尝(二)加载数据
关于安卓SVGA浅尝(二)加载数据 相关链接 SVGA官网 SVGA-github说明文档 背景 项目开发,都会和动画打交道,动画的方案选取,就有很多选择。如Json动画,svga动画,gif等等。各有各的优势。目前项…...
使用matlab产生二维动态曲线视频文件具体举例
使用matlab产生二维动态曲线视频文件举例 在进行有些函数变化过程时候,需要用到直观的动态显示,本博文将举例说明利用Matlab编程进行二维动态曲线的生成视频文件。 一、问题描述 利用matlab编程实现 y 1 s i n ( t ) , y 2 c o s ( t ) , y 3 s i …...
Selenium自动化测试框架常见异常分析及解决方法
01 pycharm中导入selenium报错 现象: pycharm中输入from selenium import webdriver, selenium标红 原因1: pycharm使用的虚拟环境中没有安装selenium, 解决方法: 在pycharm中通过设置或terminal面板重新安装selenium 原因2: 当前项目下有selenium.py,和系统包名冲突导致, …...

[TI] [Textual Inversion] An image is worth an word
自己的理解: 根据几个图像,找出来一个关键字可以代表它们,然后我们可以再用这个关键字去生成新的东西。 提出关键字 1 Introduction word->token->embedding Textual Inversion过程 需要: ① a fixed, pre-trained text…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
