人工智能AI 全栈体系(六)
第一章 神经网络是如何实现的
这些年神经网络的发展越来越复杂,应用领域越来越广,性能也越来越好,但是训练方法还是依靠 BP 算法。也有一些对 BP 算法的改进算法,但是大体思路基本是一样的,只是对 BP 算法个别地方的一些小改进,比如变步长、自适应步长等。还有就是,由于训练数据存在噪声,训练神经网络时也并不是损失函数越小越好。当损失函数特别小时,可能会出现所谓的“过拟合”问题,导致神经网络在实际使用时性能严重下降。
六、过拟合问题

1. 什么是过拟合问题?
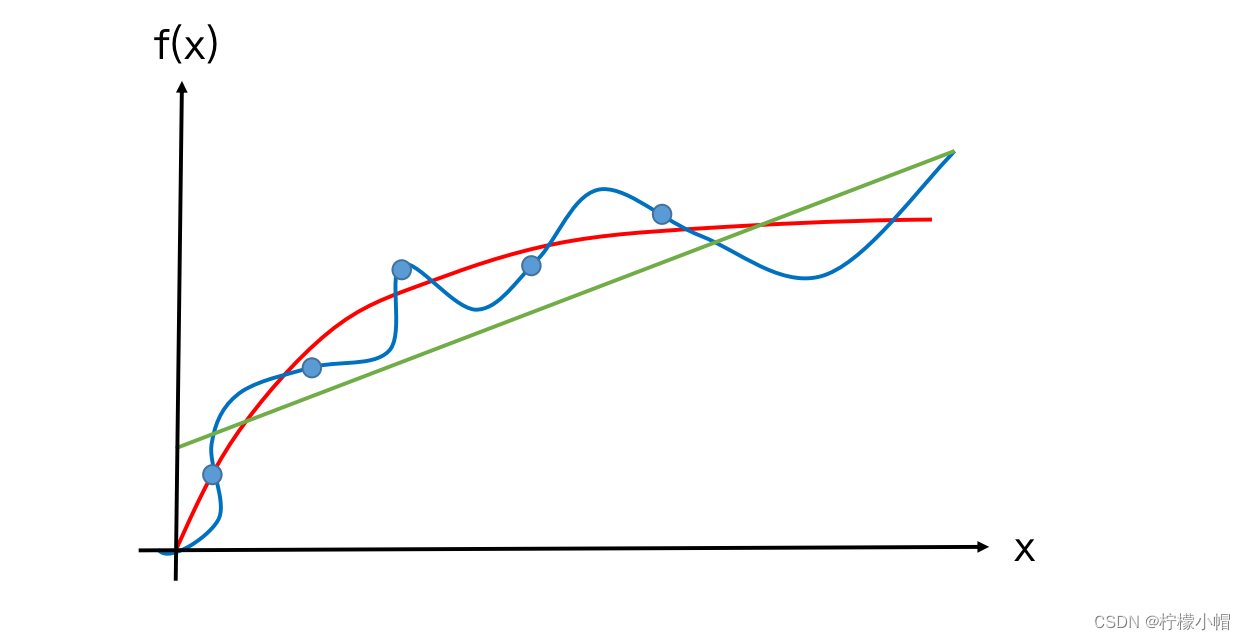
- 上图中蓝色圆点给出的是 6 个样本点,假设这些样本点来自于某个曲线的采样,但是我们又不知道原曲线是什么样子,如何根据这 6 个样本点“恢复”出原曲线呢?这就是拟合问题。下图给出了 3 种拟合方案,其中绿色的是一条直线,显然拟合的有些粗糙,蓝色曲线有点复杂,经过了每一个样本点,该曲线与 6 个采样点完美地拟合在一起,似乎是个不错的结果,但是为此付出的代价是曲线弯弯曲曲,感觉是为拟合而拟合,没有考虑 6 个样本点的分布趋势。考虑到采样过程中往往是含有噪声的,这种所谓的完美拟合其实并不完美。红色曲线虽然没有经过每个样本点,但是更能反映 6 个样本点的分布趋势,很可能更接近于原曲线,所以有理由认为红色曲线更接近原始曲线,是我们想要的拟合结果。如果我们用拟合函数与样本点的误差平方和作为拟合好坏的评价,也就是损失函数,绿色曲线由于距离样本点比较远,损失函数最大,蓝色曲线由于经过了每个样本点,误差为 0,损失函数最小,而红色曲线的损失函数介于二者之间。绿色曲线由于拟合的不够,我们称作欠拟合,蓝色曲线由于拟合过渡,我们称为过拟合,而红色曲线是我们希望的拟合结果。在神经网络的训练中,也会出现类似的欠拟合和过拟合的问题。
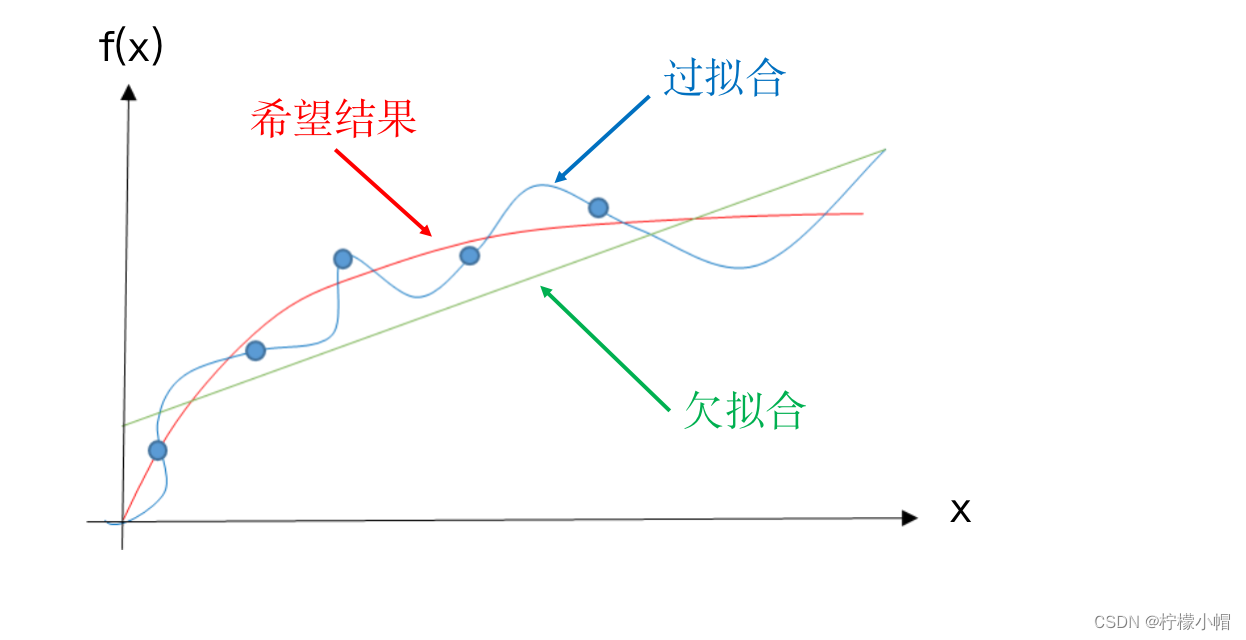
- 欠拟合显然是不好的结果,过拟合会带来什么问题呢?
2. 神经网络的过拟合问题
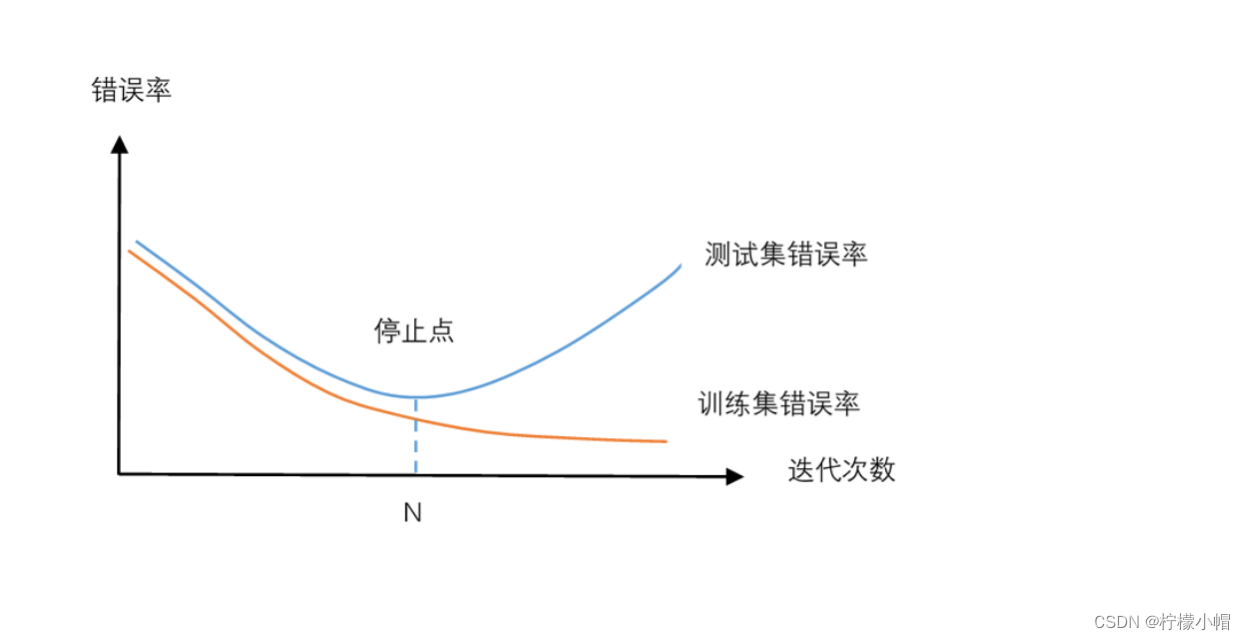
- 我们把样本集分成训练集和测试集两个集合,训练集用于神经网络的训练,测试集用于测试神经网络的性能。如上图所示,纵坐标是错误率,横坐标是训练时的迭代轮次。红色曲线是在训练集上的错误率,蓝色曲线是测试集上的错误率。每经过一定的训练迭代轮次后,就测试一次训练集和测试集上的错误率。从图中可以发现,在训练的开始阶段,由于处于欠拟合状态,无论是训练集上的错误率还是测试集上的错误率,都随着训练的进行逐步下降。但是当训练迭代轮次达到 N 次后,测试集上的错误率反而逐步上升了,这就是出现了过拟合现象。测试集上的错误率相当于神经网络在实际使用中的表现,因此我们希望得到一个合适的拟合,使得测试集上的错误率最小,所以应该在迭代轮次达到 N 次时,就结束训练,以防止出现过拟合现象。
- 训练时并不是损失函数越小越好。
- 何时开始出现过拟合并不容易判断。一种简单的方法就是使用测试集,做出像上图那样的错误率曲线,找到 N 点,用在 N 点得到的参数值作为神经网络的参数值就可以了。
- 但这种方法要求样本集合比较大才行,因为无论是训练还是测试都需要比较多的样本才行。而实际使用时往往是面临样本不足的问题。
- 为解决过拟合问题,研究者提出了一些方法,可以有效缓解过拟合问题。当然每种方法都不是万能的,只能说在一定程度上弱化了过拟合问题。
3. 减少过拟合的方法:正则化项法
- BP算法时,用的损失函数是:
E d ( w ) = ∑ k = 1 M ( t k d − o k d ) 2 E_d(w) = \sum^{M}_{k=1}{(t_{kd} - o_{kd})^2} Ed(w)=k=1∑M(tkd−okd)2
- 在这个损失函数上增加一个正则化项 ∥ w ∥ 2 2 \begin{Vmatrix}w\\\end{Vmatrix}_2^2 w 22 ,变成:
E d ( w ) = ∑ k = 1 M ( t k d − o k d ) 2 + ∥ w ∥ 2 2 E_d(w) = \sum^{M}_{k=1}{(t_{kd} - o_{kd})^2} + \begin{Vmatrix}w\\\end{Vmatrix}_2^2 Ed(w)=k=1∑M(tkd−okd)2+ w 22 - 其中 ∥ w ∥ 2 2 \begin{Vmatrix}w\\\end{Vmatrix}_2^2 w 22 表示权重w的2-范数, ∥ w ∥ 2 2 \begin{Vmatrix}w\\\end{Vmatrix}_2^2 w 22 表示2-范数的平方。
- w的2-范数就是每个权重 w i w_i wi 平方后求和再开方,这里用的是2-范数的平方,所以就是权重的平方和了。如果用 w i ( i = 1 , 2 , . . . , N ) w_i(i=1,2,...,N) wi(i=1,2,...,N) 表示第i个权重,则:
∥ w ∥ 2 2 = w 1 2 + w 2 2 + ⋯ + w N 2 \begin{Vmatrix}w\\\end{Vmatrix}_2^2 = w_1^2 + w_2^2 + \cdots + w_N^2 w 22=w12+w22+⋯+wN2 - 当然这里并不局限于2-范数,也可以用其他的范数。

4. 正则化项的作用:降低模型复杂性
- 为什么增加了正则化项后就可以避免过拟合呢?
- 添加了正则化项的损失函数,相当于在最小化损失函数的同时,要求权重也尽可能地小,相当于限制了权重的变化范围。
- 以下图所示的曲线拟合为例说明,作为一般的情况,一个曲线拟合函数f(x)可以认为是如下形式:
f ( x ) = w 0 + w 1 x + w 2 x 2 + ⋯ + w n x n f(x) = w_0 + w_1x + w_2x^2 + \cdots + w_nx^n f(x)=w0+w1x+w2x2+⋯+wnxn - 如果f(x)中包含的 x n x_n xn 项越多,n越大,则f(x)越可以表示复杂的曲线,拟合能力就越强,也更容易造成过拟合。
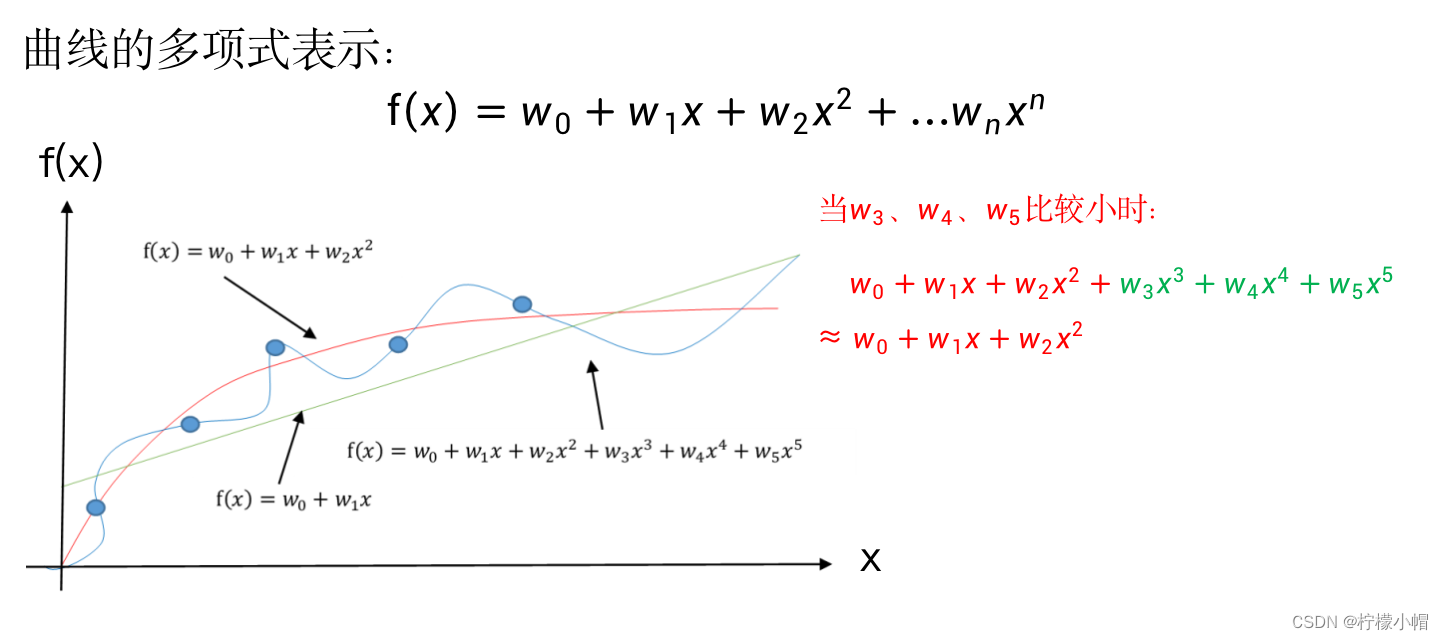
- 比如在上图所示的3条曲线,绿色曲线是个直线,其形式为:
f ( x ) = w 0 + w 1 x f(x) = w_0 + w_1x f(x)=w0+w1x - 只含有x项,只能表示直线,所以就表现为欠拟合。而对于其中的蓝色曲线,其形式为:
f ( x ) = w 0 + w 1 x + w 2 x 2 + w 3 x 3 + w 4 x 4 + w 5 x 5 f(x) = w_0 + w_1x + w_2x^2 + w_3x^3 + w_4x^4 + w_5x^5 f(x)=w0+w1x+w2x2+w3x3+w4x4+w5x5
含有5个 x n x^n xn 项,表达能力比较强,从而造成了过拟合。而对于其中的红色曲线,其形式为:
f ( x ) = w 0 + w 1 x + w 2 x 2 f(x) = w_0 + w_1x + w_2x^2 f(x)=w0+w1x+w2x2
含有2个 x n x^n xn 项,对于这个问题来说,可能刚好合适,所以体现了比较好的拟合效果。但是在实际当中呢,我们很难知道应该有多少个 x n x^n xn 项是合适的,有可能 x n x^n xn 项是比较多的,通过在损失函数中加入正则化项,使得权重w尽可能地小,在一定程度上可以限制过拟合情况的发生。比如对于蓝色曲线:
f ( x ) = w 0 + w 1 x + w 2 x 2 + w 3 x 3 + w 4 x 4 + w 5 x 5 f(x) = w_0 + w_1x + w_2x^2 + w_3x^3 + w_4x^4 + w_5x^5 f(x)=w0+w1x+w2x2+w3x3+w4x4+w5x5
虽然它含有5个 x n x^n xn 项,但是如果我们最终得到的 w 3 w_3 w3 、 w 4 w_4 w4 、 w 5 w_5 w5 都比较小的话,那么也就与红色曲线:
f ( x ) = w 0 + w 1 x + w 2 x 2 f(x) = w_0 + w_1x + w_2x^2 f(x)=w0+w1x+w2x2
比较接近了。 - 对于一个复杂的神经网络来说,一般具有很强的表达能力,如果不采取专门的方法加以限制的话,很容易造成过拟合。
5. L2(2-范数)正则化项
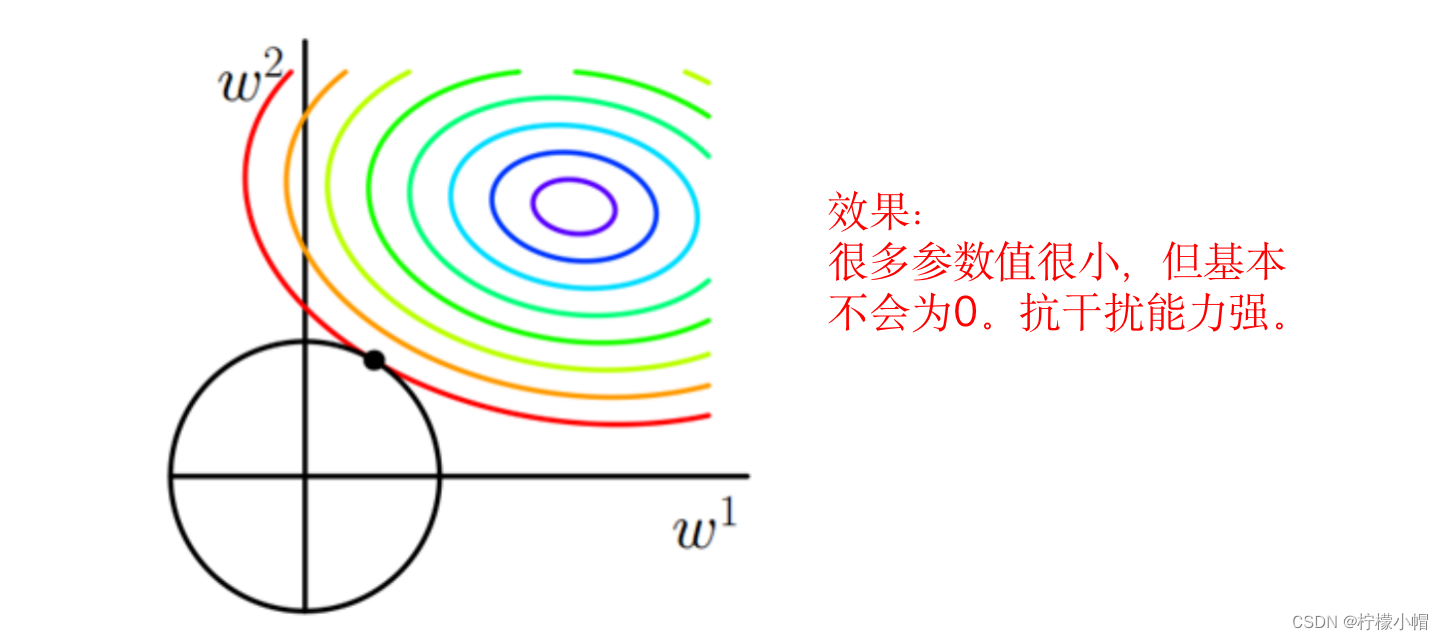
6. L1(1-范数)正则化项
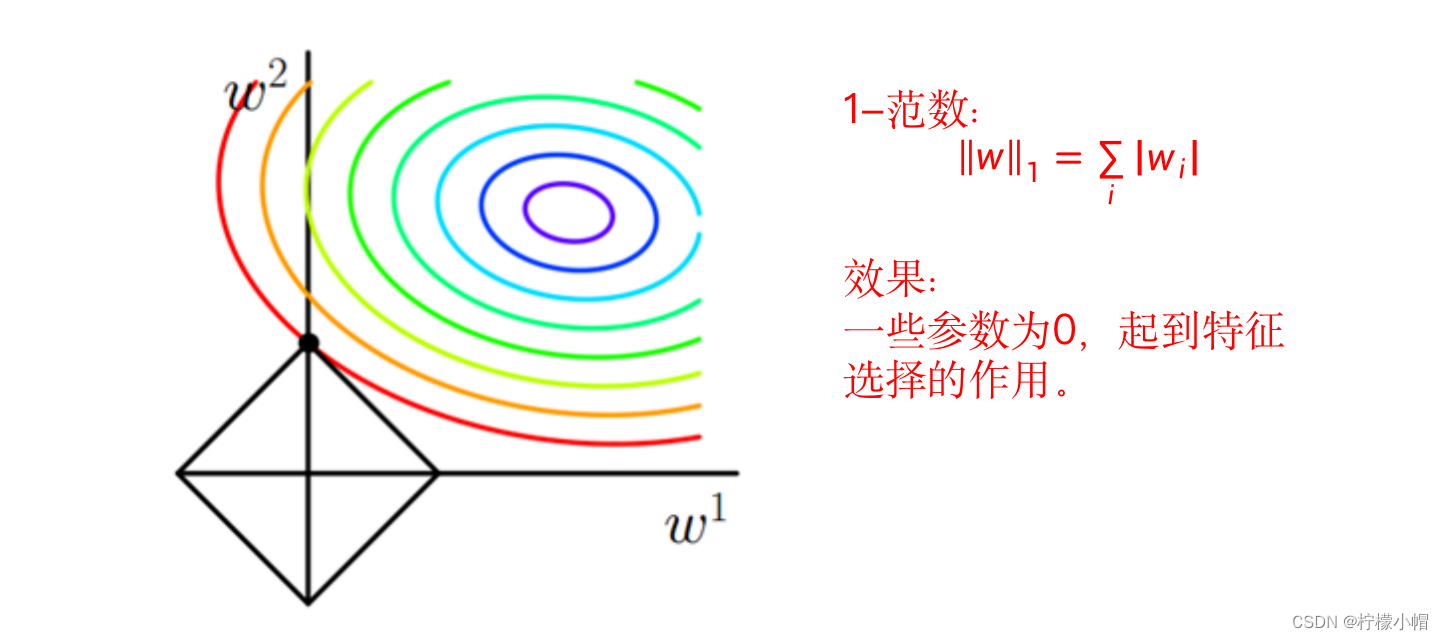
7. 减少过拟合的方法:舍弃法(Dropout)
- 所谓的舍弃法,就是在训练神经网络的过程中,随机地临时删除一些神经元,只对剩余的神经元进行训练。哪些神经元被舍弃是随机的,并且是临时的,只在这次权重更新中被舍弃,下一次更新时哪些神经元被舍弃,再重新随机选择,也就是说每进行一次权重更新,都要重新做一次随机舍弃。下图给出了一个舍弃示意图,图中虚线所展示的神经元表示被临时舍弃了,可以认为这些神经元被临时从神经网络中删除了。舍弃只发生在训练时,训练完成后在使用神经网络时,所有神经元都被使用。
- 一个神经网络含有的神经元越多,表达能力越强,越容易造成过拟合。所以简单地理解就是在训练阶段,通过舍弃减少神经元的数量,得到一个简化的神经网络,降低了神经网络的表达能力。但是由于每次舍弃的神经元又是不一样的,相当于训练了多个简化的神经网络,在使用神经网络时又是使用所有神经元,所以相当于多个简化的神经网络集成在一起使用,既可以减少过拟合,又能保持神经网络的性能。举一个例子说明这样做的合理性。比如有 10 个同学组成一个小组做实验,如果 10 个同学每次都一起做,很可能就是两三个学霸在起主要作用,其他同学得不到充分的训练。但是如果引入“舍弃机制”,每次都随机地从 10 名同学中选取 5 名同学做实验,这样会有更多的同学得到了充分的训练。当 10 名同学组合在一起开展研究时,由于每个同学都得到了充分的训练,所以 10 人组合在一起会具有更强的研究能力。
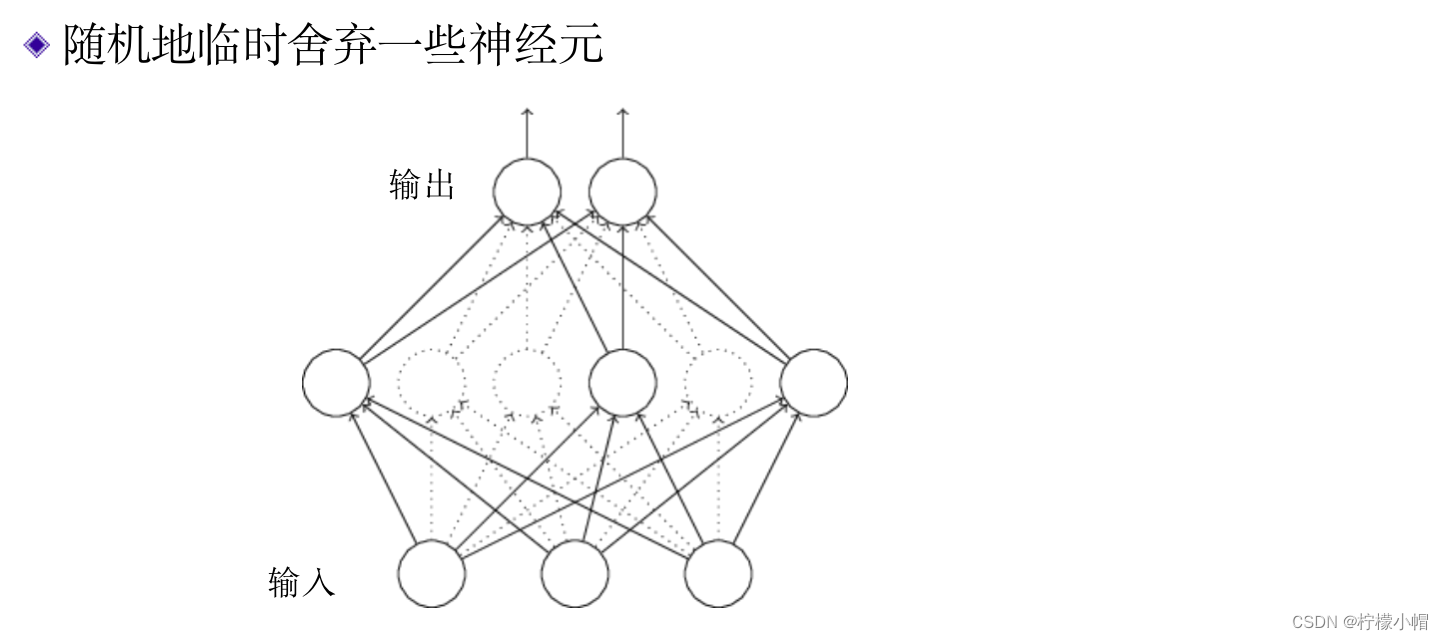
- 舍弃是在神经网络的每一层进行的,除了输入层和输出层外,每一层都会发生舍弃,舍弃的比例大概在50%左右,也就是说在神经网络的每一层,都大约舍弃掉50%左右的神经元。
8. 减少过拟合的方法:数据增强法
- 在曲线拟合中,如果数据足够多,过拟合的风险就会变小,因为足够多的数据会限制拟合函数的激烈变化,使得拟合函数更接近原函数。
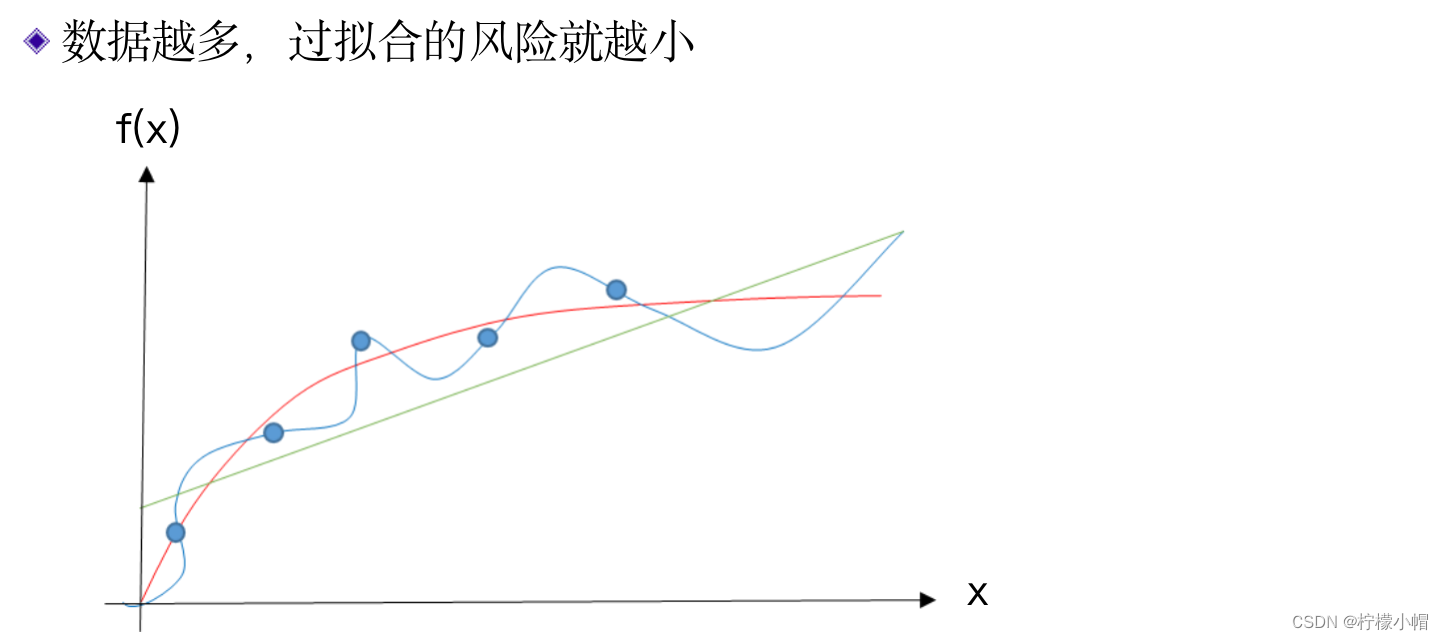
9. 如何获得更多的数据?
- 除了尽可能收集更多的数据外,可以利用已有的数据产生一些新数据。比如想识别猫和狗,我们已经有了一些猫和狗的图片,那么可以通过旋转、缩放、局部截取、改变颜色等方法,将一张图片变换成很多张图片,使得训练样本数量数十倍、数百倍地增加。实验表明,通过数据增强可以有效提高神经网络的性能。

10. 总结

- 由于数据存在噪声等原因,在神经网络的训练过程中并不是损失函数越小越好,因为当训练到一定程度后,进一步减少训练集上的误差,反而会加大在测试集上的误差。这一现象称为过拟合。
- 有三种减少过拟合的方法:
(1)正则项法。也就是在损失函数中增加正则项,让权重尽可能地小,达到防止过拟合的目的。
(2)舍弃法。在训练过程中,随机地临时舍弃一部分神经元,每次舍弃都相当于只训练一个子网络。其结果相当于训练了多个子网络再集成在一起使用,网络的每个部分都得到了充分的训练,从而提高了神经网络的整体性能。
(3)数据增强法。一般来说,训练数据越大,训练的神经网络性能会越好。当没有足够多的训练数据时,可以通过对已有数据进行处理产生新的数据的办法,增大训练数据。这一方法称为数据增强方法。比如对于图像数据,可以通过旋转、缩放、局部截取、改变颜色等方法,将一张图片变换成很多张图片,使得训练样本数量数十倍、数百倍地增加。
相关文章:

人工智能AI 全栈体系(六)
第一章 神经网络是如何实现的 这些年神经网络的发展越来越复杂,应用领域越来越广,性能也越来越好,但是训练方法还是依靠 BP 算法。也有一些对 BP 算法的改进算法,但是大体思路基本是一样的,只是对 BP 算法个别地方的一…...
NPDP是什么?考了有用吗?
1)NPDP是什么? NPDP,全称为New Product Development Professional,即新产品开发专业人员。NPDP认证是由世界产品开发协会(PDMA)推出的一项专业认证。它旨在评估和认可个人在新产品开发领域的专业知识和技能…...

关于安卓SVGA浅尝(二)加载数据
关于安卓SVGA浅尝(二)加载数据 相关链接 SVGA官网 SVGA-github说明文档 背景 项目开发,都会和动画打交道,动画的方案选取,就有很多选择。如Json动画,svga动画,gif等等。各有各的优势。目前项…...
使用matlab产生二维动态曲线视频文件具体举例
使用matlab产生二维动态曲线视频文件举例 在进行有些函数变化过程时候,需要用到直观的动态显示,本博文将举例说明利用Matlab编程进行二维动态曲线的生成视频文件。 一、问题描述 利用matlab编程实现 y 1 s i n ( t ) , y 2 c o s ( t ) , y 3 s i …...
Selenium自动化测试框架常见异常分析及解决方法
01 pycharm中导入selenium报错 现象: pycharm中输入from selenium import webdriver, selenium标红 原因1: pycharm使用的虚拟环境中没有安装selenium, 解决方法: 在pycharm中通过设置或terminal面板重新安装selenium 原因2: 当前项目下有selenium.py,和系统包名冲突导致, …...

[TI] [Textual Inversion] An image is worth an word
自己的理解: 根据几个图像,找出来一个关键字可以代表它们,然后我们可以再用这个关键字去生成新的东西。 提出关键字 1 Introduction word->token->embedding Textual Inversion过程 需要: ① a fixed, pre-trained text…...

remote: The project you were looking for could not be found
git拉取公司项目时报错: remote: The project you were looking for could not be found 发生这个问题的原因,在于git账号可能并未真正登录。 我们可以通过打开电脑的凭据管理器,查看git当前的登录是否正常。 参考链接:参考...
https跳过SSL认证时是不是就是不加密的,相当于http?
https跳过SSL认证时是不是就是不加密的,相当于http?,其实不是,HTTPS跳过SSL认证并不相当于HTTP,也不意味着没有加密。请注意以下几点: HTTPS(Hypertext Transfer Protocol Secure)本质上是在HTTP的基础上…...
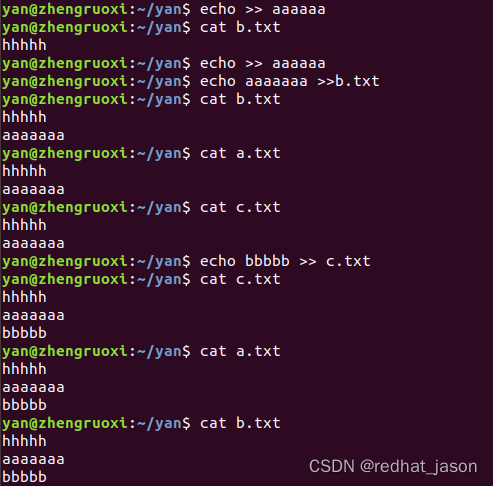
linux下链接
linux下链接用法 ln链接格式与介绍 linux下链接用法一、链接的使用格式二、链接的介绍 一、链接的使用格式 链接: 格式: ln 源文件 链接文件 硬链接 ln -s 源文件 链接文件 软连接 硬链接文件占磁盘空间 但是删除源文件不会影响硬链接文件 软链接文件不…...
OpenCV项目开发实战--主成分分析(PCA)的特征脸应用(附C++/Python实现源码)
什么是主成分分析? 这是理解这篇文章的先决条件。 图 1:使用蓝线和绿线显示 2D 数据的主要组成部分(红点)。 快速回顾一下,我们了解到第一个主成分是数据中最大方差的方向。第二主成分是空间中与第一主成分垂直(正交)的最大方差方向,依此类推。第一和第二主成分红点(2…...
多层感知机——MLP
源代码在此处:https://github.com/wepe/MachineLearning/tree/master/DeepLearning Tutorials/mlp 一、多层感知机(MLP)原理简介 多层感知机(MLP,Multilayer Perceptron)也叫人工神经网络(ANN&…...

HttpClientr入门
HttpClientr入门 介绍 HttpClient是Apache Jakarta Common下的子项目,可以用来提供高效的,最新的、功能丰富的支持HTTP协议的客户端编程工具包,并且它支持HTTP协议的版本和建议。 依赖导入 <dependency><groupId>org.apache.…...

网关-开放API接口签名验证方案
接口安全问题 请求身份是否合法?请求参数是否被篡改?请求是否唯一? AppId&AppSecret 请求身份 为开发者分配AppId(开发者标识,确保唯一)和AppSecret(用于接口加密,确保不易被…...

Linux知识点 -- 网络基础 -- 传输层
Linux知识点 – 网络基础 – 传输层 文章目录 Linux知识点 -- 网络基础 -- 传输层一、传输层协议1.端口号2.网络相关bash命令 二、UDP协议1.UDP报文的解包与交付2.理解UDP报文3.UDP协议的特点4.UDP应用层IO类接口5.UDP的缓冲区6.UDP使用注意事项7.基于UDP的应用层协议 三、TCP协…...

计算机视觉与深度学习-经典网络解析-AlexNet-[北邮鲁鹏]
这里写目录标题 AlexNet参考文章AlexNet模型结构AlexNet共8层:AlexNet运作流程 简单代码实现重要说明重要技巧主要贡献 AlexNet AlexNet 是一种卷积神经网络(Convolutional Neural Network,CNN)的架构。它是由Alex Krizhevsky、Il…...
)
Django学习笔记-实现联机对战(下)
笔记内容转载自 AcWing 的 Django 框架课讲义,课程链接:AcWing Django 框架课。 CONTENTS 1. 编写移动同步函数move_to2. 编写攻击同步函数shoot_fireball 1. 编写移动同步函数move_to 与上一章中的 create_player 同步函数相似,移动函数的同…...

一文了解什么SEO
搜索引擎优化 (SEO) 是一门让页面在 Google 等搜索引擎中排名更高的艺术和科学。 一、搜索引擎优化的好处 搜索引擎优化是在线营销的关键部分,因为搜索是用户浏览网络的主要方式之一。 搜索结果以有序列表的形式呈现,网站在该列表中的排名越高&#x…...

SpringBoot+Jpa+Thymeleaf实现增删改查
SpringBootJpaThymeleaf实现增删改查 这篇文章介绍如何使用 Jpa 和 Thymeleaf 做一个增删改查的示例。 1、pom依赖 pom 包里面添加Jpa 和 Thymeleaf 的相关包引用 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.…...
最快的包管理器--pnpm创建vue项目完整步骤
1.用npm全局安装pnpm npm install -g pnpm 2.在要创建vue项目的包下进入cmd,输入: pnpm create vue 3.输入项目名字,选择Router,Pinia,ESLint,Prettier之后点确定 4.cd到创建好的项目 ,安装依赖 cd .\刚创建好的项目名称\ p…...

算法通过村第九关-二分(中序遍历)黄金笔记|二叉搜索树
文章目录 前言1. 有序数组转二叉搜索树2. 寻找连个正序数组的中位数总结 前言 提示:有时候,我感觉自己一辈子活在两个闹钟之间,早上的第一次闹钟,以及5分钟之后的第二次闹钟。 --奥利弗萨克斯《意识的河流》 每个专题都有简单题&a…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
