多层感知机——MLP
源代码在此处:https://github.com/wepe/MachineLearning/tree/master/DeepLearning Tutorials/mlp
一、多层感知机(MLP)原理简介
多层感知机(MLP,Multilayer Perceptron)也叫人工神经网络(ANN,Artificial Neural Network),除了输入输出层,它中间可以有多个隐层,最简单的MLP只含一个隐层,即三层的结构,如下图:

从上图可以看到,多层感知机层与层之间是全连接的。多层感知机最底层是输入层,中间是隐藏层,最后是输出层。
隐藏层的神经元怎么得来?首先它与输入层是全连接的,假设输入层用向量X表示,则隐藏层的输出就是 f (W1X+b1),W1是权重(也叫连接系数),b1是偏置,函数f 可以是常用的sigmoid函数或者tanh函数:
1.为什么使用激活函数?
a. 不使用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合。
b. 使用激活函数,能够给神经元引入非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以利用到更多的非线性模型中。
2. sigmod 函数

导数为:
![]()
sigmod函数业也叫Logistic函数,用于隐藏层神经元输出,取值范围为(0,1),它可以将一个实数映射到区间(0,1)上,可以用来做二分类。在特征相差比较复杂或相差不是特别大时效果比较好。
缺点:
激活函数计算量大,反向传播求误差梯度时,求导设计除法。
反向传播时,很容易出现梯度消失的情况,从而无法完成深层网络的训练。
3.tanh函数

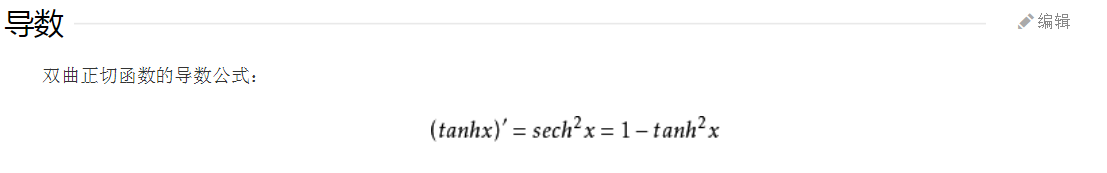
取值范围为[-1,1]
tanh在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。
与sigmod的区别是 tanh 是0 的均值,因此在实际应用中tanh会比sigmod更好。
在具体应用中,tanh函数相比于Sigmoid函数往往更具有优越性,这主要是因为Sigmoid函数在输入处于[-1,1]之间时,函数值变 化敏感,一旦接近或者超出区间就失去敏感性,处于饱和状态。
其实隐藏层到输出层可以看成是一个多类别的逻辑回归,也即softmax回归,所以输出层的输出就是softmax(W2X1+b2),X1表示隐藏层的输出f(W1X+b1)。
MLP整个模型就是这样子的,上面说的这个三层的MLP用公式总结起来就是,函数G是softmax。
因此,MLP所有的参数就是各个层之间的连接权重以及偏置,包括W1、b1、W2、b2。对于一个具体的问题,怎么确定这些参数?求解最佳的参数是一个最优化问题,解决最优化问题,最简单的就是梯度下降法了(SGD):首先随机初始化所有参数,然后迭代地训练,不断地计算梯度和更新参数,直到满足某个条件为止(比如误差足够小、迭代次数足够多时)。这个过程涉及到代价函数、规则化(Regularization)、学习速率(learning rate)、梯度计算等,本文不详细讨论,读者可以参考本文底部给出的两个链接。
了解了MLP的基本模型,下面进入代码实现部分:
二、多层感知机(MLP)代码详细解读(基于python+theano)
概括地说,MLP的输入层X其实就是我们的训练数据,所以输入层不用实现,剩下的就是“输入层到隐含层”,“隐含层到输出层”这两部分。上面介绍原理时已经说到了,“输入层到隐含层”就是一个全连接的层,在下面的代码中我们把这一部分定义为HiddenLayer。“隐含层到输出层”就是一个分类器softmax回归,在下面的代码中我们把这一部分定义为logisticRegression。
直接上代码:
# -*- coding: utf-8 -*-
"""
@author:wepon
@blog:http://blog.csdn.net/u012162613/article/details/43221829注释:
MLP多层感知机层与层之间是全连接的,以三层为例,最底层是输入层,中间是隐藏层,最后是输出层。
输入层没什么好说,你输入什么就是什么,比如输入是一个n维向量,就有n个神经元。
隐藏层的神经元怎么得来?它与输入层是全连接的,假设输入是X,则隐藏层的输出就是
f(WX+b),W是权重,b是偏置,f可以是常用的sigmoid函数或者tanh函数。
最后就是输出层,输出层与隐藏层是什么关系?其实隐藏层到输出层可以看成时一个多类别的逻辑回归,也即softmax,所以输出层的输出就是softmax(W1X1+b1),X1表示隐藏层的输出。
MLP整个模型就是这样子的,它所有的参数就是各个层之间的连接权重以及偏置,包括W、b、W1、b1。对于一个具体的问题,怎么确定这些参数?那就是梯度下降法了(SGD),首先随机初始化所有参数,然后迭代地训练,不断地更新参数,直到满足某个条件为止(比如误差足够小、迭代次数足够多时)。
"""
__docformat__ = 'restructedtext en'
import os
import sys
import time
import gzip
import cPickleimport numpy
import theano
import theano.tensor as T
"""
注释:
这是定义隐藏层的类,首先明确:隐藏层的输入即input,输出即隐藏层的神经元个数。输入层与隐藏层是全连接的。
假设输入是n_in维的向量(也可以说时n_in个神经元),隐藏层有n_out个神经元,则因为是全连接,
一共有n_in*n_out个权重,故W大小时(n_in,n_out),n_in行n_out列,每一列对应隐藏层的每一个神经元的连接权重。
b是偏置,隐藏层有n_out个神经元,故b时n_out维向量。
rng即随机数生成器,numpy.random.RandomState,用于初始化W。
input训练模型所用到的所有输入,并不是MLP的输入层,MLP的输入层的神经元个数时n_in,而这里的参数input大小是(n_example,n_in),每一行一个样本,即每一行作为MLP的输入层。
activation:激活函数,这里定义为函数tanh
"""
class HiddenLayer(object):
def __init__(self, rng, input, n_in, n_out, W=None, b=None,
activation=T.tanh):
self.input = input #类HiddenLayer的input即所传递进来的input"""
注释:
代码要兼容GPU,则必须使用 dtype=theano.config.floatX,并且定义为theano.shared
另外,W的初始化有个规则:如果使用tanh函数,则在-sqrt(6./(n_in+n_hidden))到sqrt(6./(n_in+n_hidden))之间均匀
抽取数值来初始化W,若时sigmoid函数,则以上再乘4倍。
"""
#如果W没有给定,即等于None,则根据上述的规则随机初始化。
#加入这个判断的原因是:有时候我们可以用训练好的参数来初始化W,见我的上一篇文章。
if W is None:
W_values = numpy.asarray(
rng.uniform(
low=-numpy.sqrt(6. / (n_in + n_out)),
high=numpy.sqrt(6. / (n_in + n_out)),
size=(n_in, n_out)
),
dtype=theano.config.floatX
)
if activation == theano.tensor.nnet.sigmoid:
W_values *= 4
W = theano.shared(value=W_values, name='W', borrow=True)if b is None:
b_values = numpy.zeros((n_out,), dtype=theano.config.floatX)
b = theano.shared(value=b_values, name='b', borrow=True)#用上面定义的W、b来初始化类HiddenLayer的W、b
self.W = W
self.b = b#隐含层的输出
lin_output = T.dot(input, self.W) + self.b
self.output = (
lin_output if activation is None
else activation(lin_output)
)#隐含层的参数
self.params = [self.W, self.b]"""
定义分类层,Softmax回归
在deeplearning tutorial中,直接将LogisticRegression视为Softmax,
而我们所认识的二类别的逻辑回归就是当n_out=2时的LogisticRegression
"""
#参数说明:
#input,大小就是(n_example,n_in),其中n_example是一个batch的大小,
#因为我们训练时用的是Minibatch SGD,因此input这样定义
#n_in,即上一层(隐含层)的输出
#n_out,输出的类别数
class LogisticRegression(object):
def __init__(self, input, n_in, n_out):#W大小是n_in行n_out列,b为n_out维向量。即:每个输出对应W的一列以及b的一个元素。
self.W = theano.shared(
value=numpy.zeros(
(n_in, n_out),
dtype=theano.config.floatX
),
name='W',
borrow=True
)self.b = theano.shared(
value=numpy.zeros(
(n_out,),
dtype=theano.config.floatX
),
name='b',
borrow=True
)#input是(n_example,n_in),W是(n_in,n_out),点乘得到(n_example,n_out),加上偏置b,
#再作为T.nnet.softmax的输入,得到p_y_given_x
#故p_y_given_x每一行代表每一个样本被估计为各类别的概率
#PS:b是n_out维向量,与(n_example,n_out)矩阵相加,内部其实是先复制n_example个b,
#然后(n_example,n_out)矩阵的每一行都加b
self.p_y_given_x = T.nnet.softmax(T.dot(input, self.W) + self.b)#argmax返回最大值下标,因为本例数据集是MNIST,下标刚好就是类别。axis=1表示按行操作。
self.y_pred = T.argmax(self.p_y_given_x, axis=1)#params,LogisticRegression的参数
self.params = [self.W, self.b]def negative_log_likelihood(self, y):
return -T.mean(T.log(self.p_y_given_x)[T.arange(y.shape[0]), y])def errors(self, y):
if y.ndim != self.y_pred.ndim:
raise TypeError(
'y should have the same shape as self.y_pred',
('y', y.type, 'y_pred', self.y_pred.type)
)
if y.dtype.startswith('int'):
return T.mean(T.neq(self.y_pred, y))
else:
raise NotImplementedError()
#3层的MLP
class MLP(object):
def __init__(self, rng, input, n_in, n_hidden, n_out):
self.hiddenLayer = HiddenLayer(
rng=rng,
input=input,
n_in=n_in,
n_out=n_hidden,
activation=T.tanh
)#将隐含层hiddenLayer的输出作为分类层logRegressionLayer的输入,这样就把它们连接了
self.logRegressionLayer = LogisticRegression(
input=self.hiddenLayer.output,
n_in=n_hidden,
n_out=n_out
)#规则化项:常见的L1、L2_sqr
self.L1 = (
abs(self.hiddenLayer.W).sum()
+ abs(self.logRegressionLayer.W).sum()
)self.L2_sqr = (
(self.hiddenLayer.W ** 2).sum()
+ (self.logRegressionLayer.W ** 2).sum()
)#损失函数Nll(也叫代价函数)
self.negative_log_likelihood = (
self.logRegressionLayer.negative_log_likelihood
)#误差
self.errors = self.logRegressionLayer.errors#MLP的参数
self.params = self.hiddenLayer.params + self.logRegressionLayer.params
# end-snippet-3
"""
加载MNIST数据集
"""
def load_data(dataset):
# dataset是数据集的路径,程序首先检测该路径下有没有MNIST数据集,没有的话就下载MNIST数据集
#这一部分就不解释了,与softmax回归算法无关。
data_dir, data_file = os.path.split(dataset)
if data_dir == "" and not os.path.isfile(dataset):
# Check if dataset is in the data directory.
new_path = os.path.join(
os.path.split(__file__)[0],
"..",
"data",
dataset
)
if os.path.isfile(new_path) or data_file == 'mnist.pkl.gz':
dataset = new_pathif (not os.path.isfile(dataset)) and data_file == 'mnist.pkl.gz':
import urllib
origin = (
'http://www.iro.umontreal.ca/~lisa/deep/data/mnist/mnist.pkl.gz'
)
print 'Downloading data from %s' % origin
urllib.urlretrieve(origin, dataset)print '... loading data'
#以上是检测并下载数据集mnist.pkl.gz,不是本文重点。下面才是load_data的开始
#从"mnist.pkl.gz"里加载train_set, valid_set, test_set,它们都是包括label的
#主要用到python里的gzip.open()函数,以及 cPickle.load()。
#‘rb’表示以二进制可读的方式打开文件
f = gzip.open(dataset, 'rb')
train_set, valid_set, test_set = cPickle.load(f)
f.close()
#将数据设置成shared variables,主要时为了GPU加速,只有shared variables才能存到GPU memory中
#GPU里数据类型只能是float。而data_y是类别,所以最后又转换为int返回
def shared_dataset(data_xy, borrow=True):
data_x, data_y = data_xy
shared_x = theano.shared(numpy.asarray(data_x,
dtype=theano.config.floatX),
borrow=borrow)
shared_y = theano.shared(numpy.asarray(data_y,
dtype=theano.config.floatX),
borrow=borrow)
return shared_x, T.cast(shared_y, 'int32')
test_set_x, test_set_y = shared_dataset(test_set)
valid_set_x, valid_set_y = shared_dataset(valid_set)
train_set_x, train_set_y = shared_dataset(train_set)rval = [(train_set_x, train_set_y), (valid_set_x, valid_set_y),
(test_set_x, test_set_y)]
return rval
#test_mlp是一个应用实例,用梯度下降来优化MLP,针对MNIST数据集
def test_mlp(learning_rate=0.01, L1_reg=0.00, L2_reg=0.0001, n_epochs=10,
dataset='mnist.pkl.gz', batch_size=20, n_hidden=500):
"""
注释:
learning_rate学习速率,梯度前的系数。
L1_reg、L2_reg:正则化项前的系数,权衡正则化项与Nll项的比重
代价函数=Nll+L1_reg*L1或者L2_reg*L2_sqr
n_epochs:迭代的最大次数(即训练步数),用于结束优化过程
dataset:训练数据的路径
n_hidden:隐藏层神经元个数
batch_size=20,即每训练完20个样本才计算梯度并更新参数
"""#加载数据集,并分为训练集、验证集、测试集。
datasets = load_data(dataset)
train_set_x, train_set_y = datasets[0]
valid_set_x, valid_set_y = datasets[1]
test_set_x, test_set_y = datasets[2]
#shape[0]获得行数,一行代表一个样本,故获取的是样本数,除以batch_size可以得到有多少个batch
n_train_batches = train_set_x.get_value(borrow=True).shape[0] / batch_size
n_valid_batches = valid_set_x.get_value(borrow=True).shape[0] / batch_size
n_test_batches = test_set_x.get_value(borrow=True).shape[0] / batch_size######################
# BUILD ACTUAL MODEL #
######################
print '... building the model'#index表示batch的下标,标量
#x表示数据集
#y表示类别,一维向量
index = T.lscalar()
x = T.matrix('x')
y = T.ivector('y')
rng = numpy.random.RandomState(1234)
#生成一个MLP,命名为classifier
classifier = MLP(
rng=rng,
input=x,
n_in=28 * 28,
n_hidden=n_hidden,
n_out=10
)#代价函数,有规则化项
#用y来初始化,而其实还有一个隐含的参数x在classifier中
cost = (
classifier.negative_log_likelihood(y)
+ L1_reg * classifier.L1
+ L2_reg * classifier.L2_sqr
)
#这里必须说明一下theano的function函数,givens是字典,其中的x、y是key,冒号后面是它们的value。
#在function被调用时,x、y将被具体地替换为它们的value,而value里的参数index就是inputs=[index]这里给出。
#下面举个例子:
#比如test_model(1),首先根据index=1具体化x为test_set_x[1 * batch_size: (1 + 1) * batch_size],
#具体化y为test_set_y[1 * batch_size: (1 + 1) * batch_size]。然后函数计算outputs=classifier.errors(y),
#这里面有参数y和隐含的x,所以就将givens里面具体化的x、y传递进去。
test_model = theano.function(
inputs=[index],
outputs=classifier.errors(y),
givens={
x: test_set_x[index * batch_size:(index + 1) * batch_size],
y: test_set_y[index * batch_size:(index + 1) * batch_size]
}
)validate_model = theano.function(
inputs=[index],
outputs=classifier.errors(y),
givens={
x: valid_set_x[index * batch_size:(index + 1) * batch_size],
y: valid_set_y[index * batch_size:(index + 1) * batch_size]
}
)#cost函数对各个参数的偏导数值,即梯度,存于gparams
gparams = [T.grad(cost, param) for param in classifier.params]
#参数更新规则
#updates[(),(),()....],每个括号里面都是(param, param - learning_rate * gparam),即每个参数以及它的更新公式
updates = [
(param, param - learning_rate * gparam)
for param, gparam in zip(classifier.params, gparams)
]train_model = theano.function(
inputs=[index],
outputs=cost,
updates=updates,
givens={
x: train_set_x[index * batch_size: (index + 1) * batch_size],
y: train_set_y[index * batch_size: (index + 1) * batch_size]
}
)
###############
# 开始训练模型 #
###############
print '... training'
patience = 10000
patience_increase = 2
#提高的阈值,在验证误差减小到之前的0.995倍时,会更新best_validation_loss
improvement_threshold = 0.995
#这样设置validation_frequency可以保证每一次epoch都会在验证集上测试。
validation_frequency = min(n_train_batches, patience / 2)
best_validation_loss = numpy.inf
best_iter = 0
test_score = 0.
start_time = time.clock()
#epoch即训练步数,每个epoch都会遍历所有训练数据
epoch = 0
done_looping = False
#下面就是训练过程了,while循环控制的时步数epoch,一个epoch会遍历所有的batch,即所有的图片。
#for循环是遍历一个个batch,一次一个batch地训练。for循环体里会用train_model(minibatch_index)去训练模型,
#train_model里面的updatas会更新各个参数。
#for循环里面会累加训练过的batch数iter,当iter是validation_frequency倍数时则会在验证集上测试,
#如果验证集的损失this_validation_loss小于之前最佳的损失best_validation_loss,
#则更新best_validation_loss和best_iter,同时在testset上测试。
#如果验证集的损失this_validation_loss小于best_validation_loss*improvement_threshold时则更新patience。
#当达到最大步数n_epoch时,或者patience<iter时,结束训练
while (epoch < n_epochs) and (not done_looping):
epoch = epoch + 1
for minibatch_index in xrange(n_train_batches):#训练时一个batch一个batch进行的minibatch_avg_cost = train_model(minibatch_index)
# 已训练过的minibatch数,即迭代次数iter
iter = (epoch - 1) * n_train_batches + minibatch_index
#训练过的minibatch数是validation_frequency倍数,则进行交叉验证
if (iter + 1) % validation_frequency == 0:
# compute zero-one loss on validation set
validation_losses = [validate_model(i) for i
in xrange(n_valid_batches)]
this_validation_loss = numpy.mean(validation_losses)print(
'epoch %i, minibatch %i/%i, validation error %f %%' %
(
epoch,
minibatch_index + 1,
n_train_batches,
this_validation_loss * 100.
)
)
#当前验证误差比之前的都小,则更新best_validation_loss,以及对应的best_iter,并且在tsetdata上进行test
if this_validation_loss < best_validation_loss:
if (
this_validation_loss < best_validation_loss *
improvement_threshold
):
patience = max(patience, iter * patience_increase)best_validation_loss = this_validation_loss
best_iter = itertest_losses = [test_model(i) for i
in xrange(n_test_batches)]
test_score = numpy.mean(test_losses)print((' epoch %i, minibatch %i/%i, test error of '
'best model %f %%') %
(epoch, minibatch_index + 1, n_train_batches,
test_score * 100.))
#patience小于等于iter,则终止训练
if patience <= iter:
done_looping = True
breakend_time = time.clock()
print(('Optimization complete. Best validation score of %f %% '
'obtained at iteration %i, with test performance %f %%') %
(best_validation_loss * 100., best_iter + 1, test_score * 100.))
print >> sys.stderr, ('The code for file ' +
os.path.split(__file__)[1] +
' ran for %.2fm' % ((end_time - start_time) / 60.))if __name__ == '__main__':
test_mlp()
相关文章:
多层感知机——MLP
源代码在此处:https://github.com/wepe/MachineLearning/tree/master/DeepLearning Tutorials/mlp 一、多层感知机(MLP)原理简介 多层感知机(MLP,Multilayer Perceptron)也叫人工神经网络(ANN&…...

HttpClientr入门
HttpClientr入门 介绍 HttpClient是Apache Jakarta Common下的子项目,可以用来提供高效的,最新的、功能丰富的支持HTTP协议的客户端编程工具包,并且它支持HTTP协议的版本和建议。 依赖导入 <dependency><groupId>org.apache.…...

网关-开放API接口签名验证方案
接口安全问题 请求身份是否合法?请求参数是否被篡改?请求是否唯一? AppId&AppSecret 请求身份 为开发者分配AppId(开发者标识,确保唯一)和AppSecret(用于接口加密,确保不易被…...

Linux知识点 -- 网络基础 -- 传输层
Linux知识点 – 网络基础 – 传输层 文章目录 Linux知识点 -- 网络基础 -- 传输层一、传输层协议1.端口号2.网络相关bash命令 二、UDP协议1.UDP报文的解包与交付2.理解UDP报文3.UDP协议的特点4.UDP应用层IO类接口5.UDP的缓冲区6.UDP使用注意事项7.基于UDP的应用层协议 三、TCP协…...

计算机视觉与深度学习-经典网络解析-AlexNet-[北邮鲁鹏]
这里写目录标题 AlexNet参考文章AlexNet模型结构AlexNet共8层:AlexNet运作流程 简单代码实现重要说明重要技巧主要贡献 AlexNet AlexNet 是一种卷积神经网络(Convolutional Neural Network,CNN)的架构。它是由Alex Krizhevsky、Il…...
)
Django学习笔记-实现联机对战(下)
笔记内容转载自 AcWing 的 Django 框架课讲义,课程链接:AcWing Django 框架课。 CONTENTS 1. 编写移动同步函数move_to2. 编写攻击同步函数shoot_fireball 1. 编写移动同步函数move_to 与上一章中的 create_player 同步函数相似,移动函数的同…...

一文了解什么SEO
搜索引擎优化 (SEO) 是一门让页面在 Google 等搜索引擎中排名更高的艺术和科学。 一、搜索引擎优化的好处 搜索引擎优化是在线营销的关键部分,因为搜索是用户浏览网络的主要方式之一。 搜索结果以有序列表的形式呈现,网站在该列表中的排名越高&#x…...

SpringBoot+Jpa+Thymeleaf实现增删改查
SpringBootJpaThymeleaf实现增删改查 这篇文章介绍如何使用 Jpa 和 Thymeleaf 做一个增删改查的示例。 1、pom依赖 pom 包里面添加Jpa 和 Thymeleaf 的相关包引用 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.…...
最快的包管理器--pnpm创建vue项目完整步骤
1.用npm全局安装pnpm npm install -g pnpm 2.在要创建vue项目的包下进入cmd,输入: pnpm create vue 3.输入项目名字,选择Router,Pinia,ESLint,Prettier之后点确定 4.cd到创建好的项目 ,安装依赖 cd .\刚创建好的项目名称\ p…...

算法通过村第九关-二分(中序遍历)黄金笔记|二叉搜索树
文章目录 前言1. 有序数组转二叉搜索树2. 寻找连个正序数组的中位数总结 前言 提示:有时候,我感觉自己一辈子活在两个闹钟之间,早上的第一次闹钟,以及5分钟之后的第二次闹钟。 --奥利弗萨克斯《意识的河流》 每个专题都有简单题&a…...

Mock.js之Element-ui搭建首页导航与左侧菜单
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《Spring与Mybatis集成整合》《springMvc使用》 ⛺️ 生活的理想,为了不断更新自己 ! 1、Mock.js的使用 1.1.什么是Mock.js Mock.js是一个模拟数据的生成器,用来帮助前…...
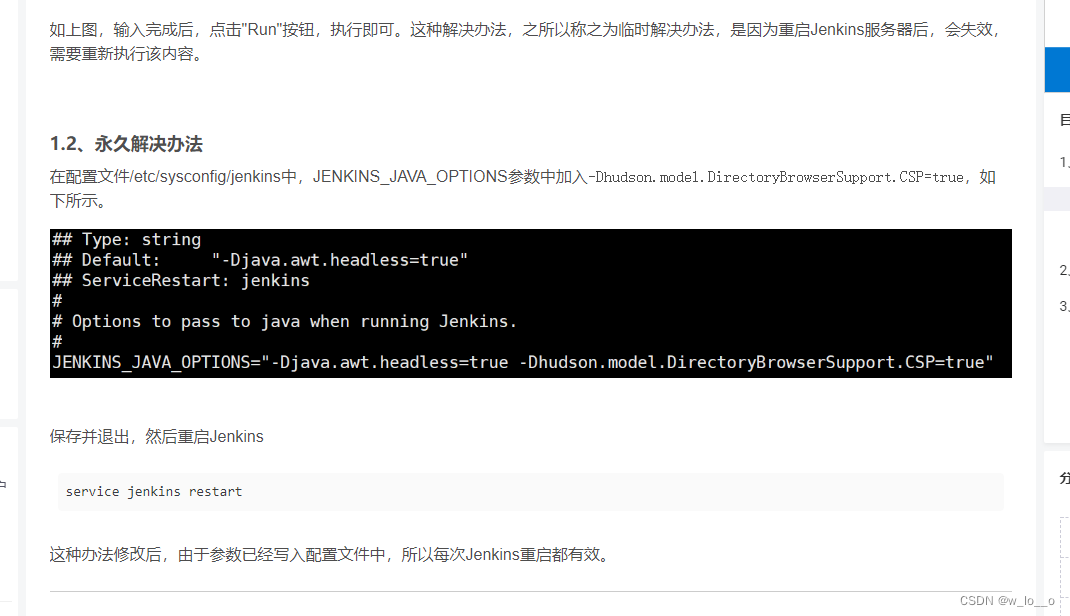
robotframework在Jenkins执行踩坑
1. Groovy Template file [robot_results.groovy] was not found in $JENKINS_HOME/email_template 1.需要在managed files 添加robot_results.groovy。这个名字需要和配置在构建项目里default content一致(Extended E-mail Notification默认设置里Default Content…...
关于ElementUI之首页导航与左侧菜单实现
目录 一.Mock 1.1.什么是Mock.js 1.2.特点 1.3.安装与配置 1.3.1. 安装mock.js 1.3.2.引入mock.js 1.4.mockjs使用 1.4.1.定义测试数据文件 1.4.2.mock拦截Ajax请求 1.4.3.界面代码优化 二.总线 2.1.是什么 2.2.前期准备 2.3.配置组件与路由关系 2.3.1. 配置组件 …...
基于springboot小区疫情防控系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

【k8s】YAML语言基础
文章目录 YAML介绍语法支持的数据类型注意事项json与yaml互转 YAML介绍 YAML是一个类似于XML、JSON的标记语言。强调以数据为中心,并不是以标记语言为中心 <heima><age>15</age><address>Beijing</address> </heima>heima:age:…...

AI时代的中国困境: ChatGPT为什么难以复制
如今,几乎所有中国互联网大厂都公布了自己的“类ChatGPT”解决方案,有些还公布了背后的关于AI技术模型的详情。 其中最高调的是百度,其“文心一言”解决方案号称即将接入数十家内容平台和数以百计的媒体、自媒体。腾讯公布的微信 AI 模型“W…...

如何使用Docker安装最新版本的Redis并设置远程访问(含免费可视化工具)
文章目录 安装Docker安装Redisredis.conf文件远程访问Redis免费可视化工具相关链接Docker是一种开源的应用容器引擎,使用Docker可以让我们快速部署应用环境,本文介绍如何使用Docker安装最新版本的Redis。 安装Docker 首先需要安装Docker,具体的安装方法可以参考Docker官方文…...
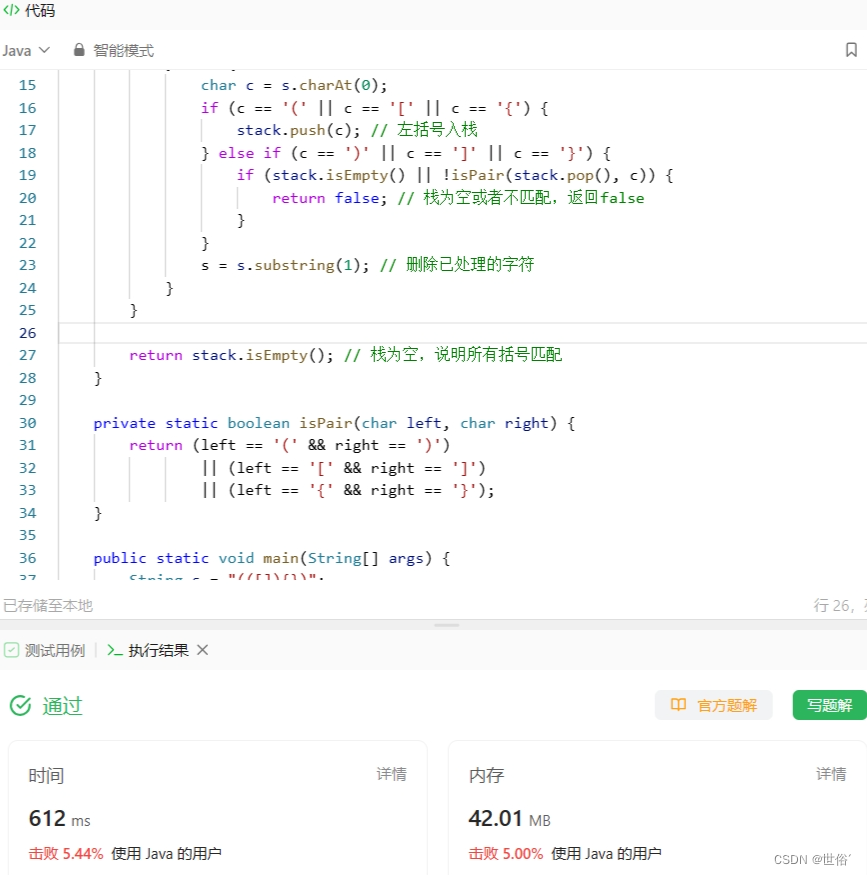
怒刷LeetCode的第8天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:双指针和排序 编辑第二题 题目来源 题目内容 解决方法 方法一:双指针 方法二:递归 方法三:快慢指针 方法四:栈 第三题 题目来源 题目内容 解决方法…...

Vue Hooks 让Vue开发更简单与高效
Vue Hooks 让Vue开发更简单与高效 介绍 Vue Hooks 是一个基于 Vue.js 的插件,它提供了一种新的方式来编写 Vue 组件,使得开发更加简单和高效。它借鉴了 React Hooks 的概念,通过使用 Hooks,我们可以在不编写类组件的情况下&…...

Go编程规范
文章目录 注释转义符定义变量方法一:指定变量类型,声明后若不赋值,使用默认值方法二:根据值自行判定变量类型(类型推导)方法三:省略var, 注意:左侧的变量不应该是已经声明过的,否则会导致编译错误[推荐]全局…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
