似然和概率
前言
高斯在处理正态分布的首次提出似然,后来英国物理学家,费歇尔

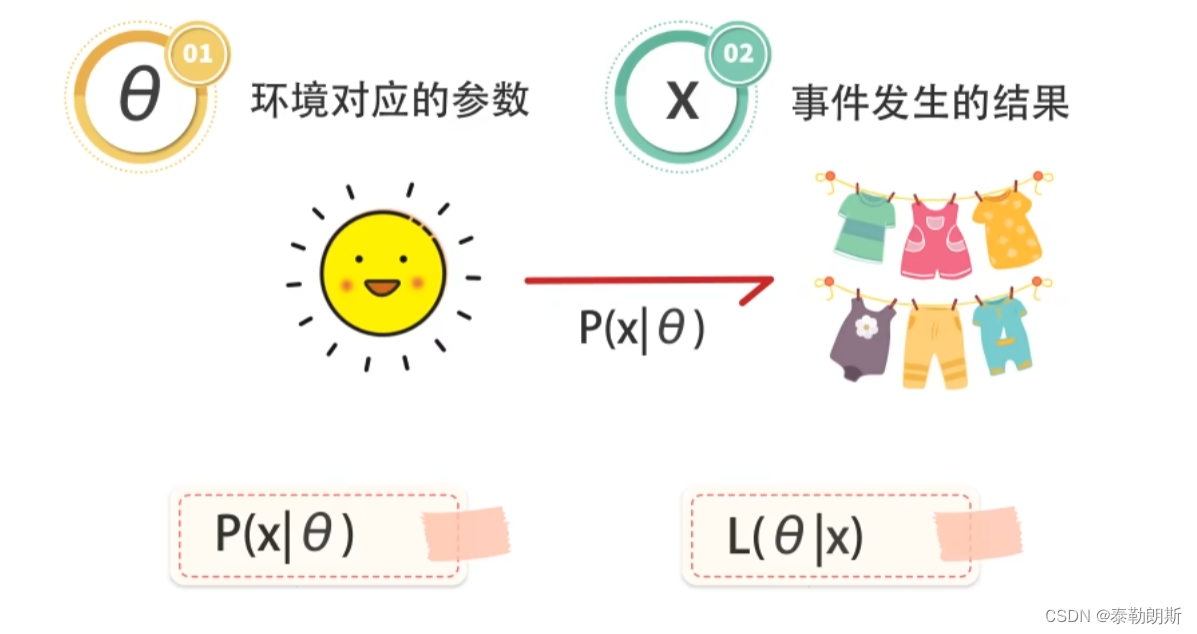
概率是抛硬币之前,根据环境推断概率

似然则相反,根据结果推论环境

P是关于x的函数,比如x为正面朝上的结果,或者反面朝上的结果,比如x=正面朝上的时候,概率 θ \theta θ是多少
L是关于 θ \theta θ的函数,就是说某一个概率值下,最有可能出现的结果
极大似然估计是根据已知的观察数据来推断模型参数的过程,根据x的结果推断 θ \theta θ,,结果x最有可能发生。
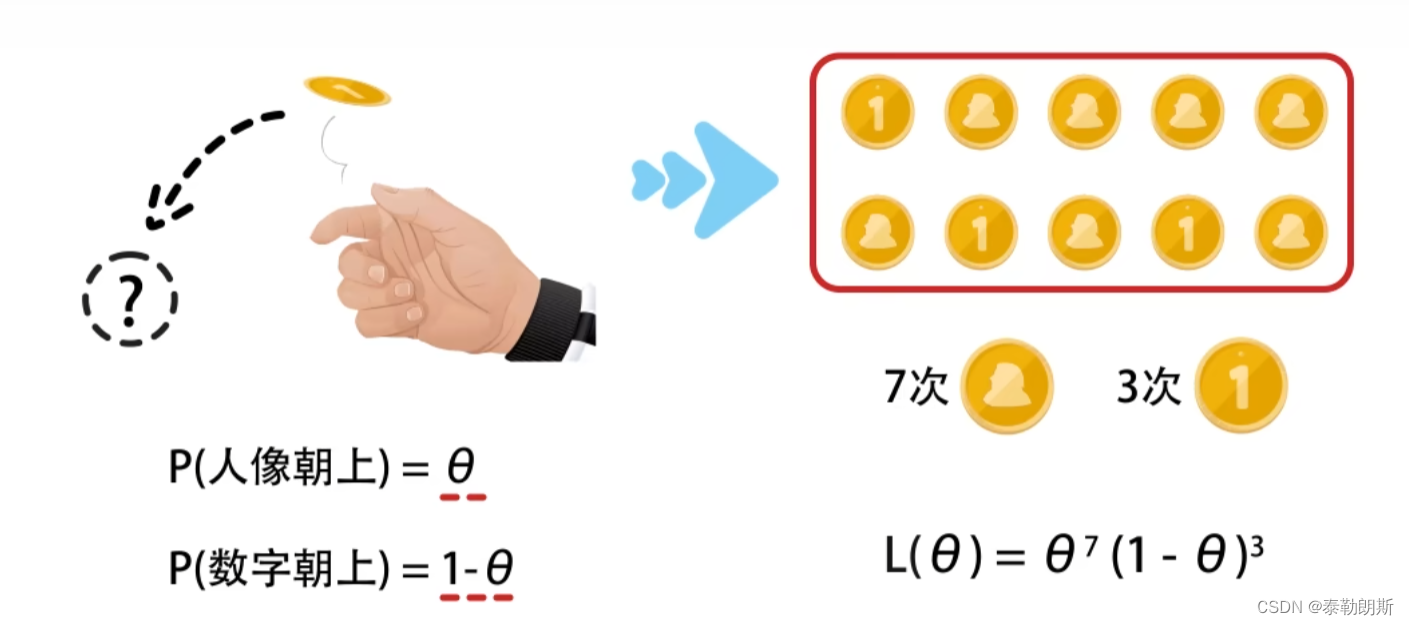
举例来说
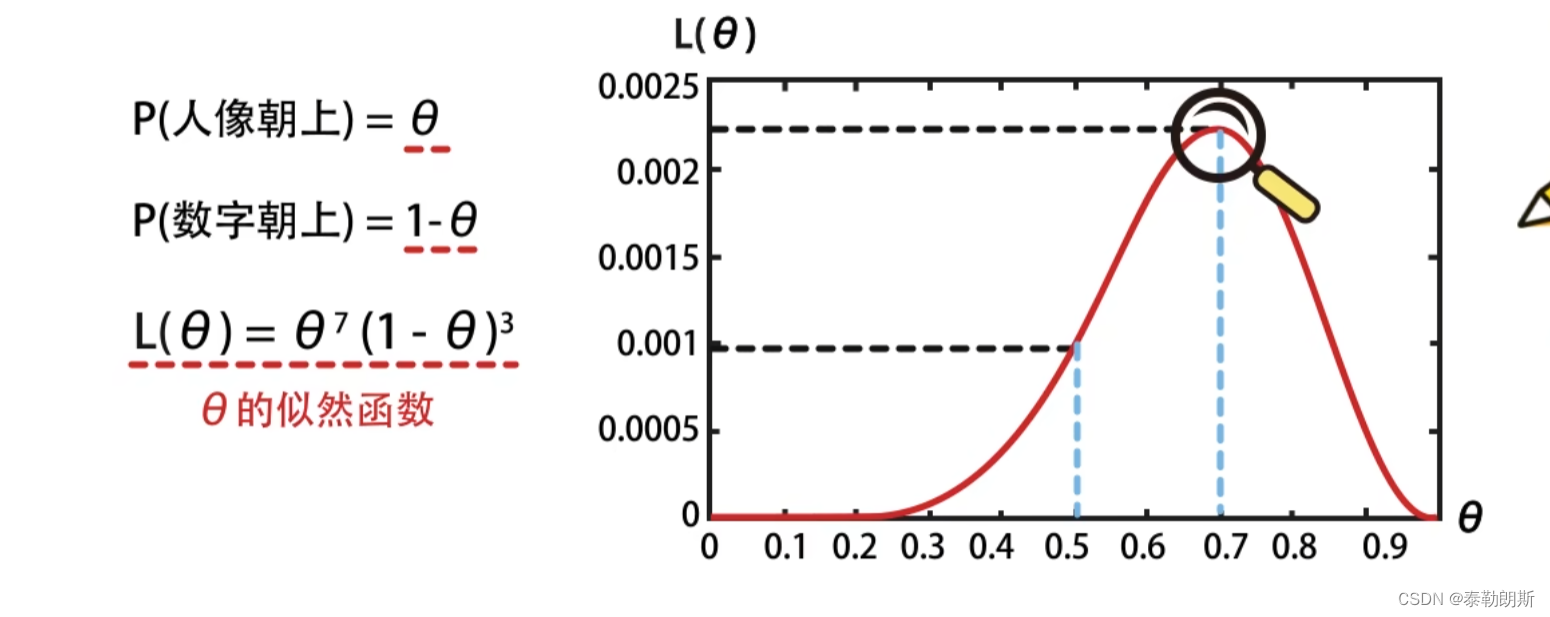
函数在 θ \theta θ未0.7的时候取得最大值
当 θ \theta θ为多少时,出现7次正面,3次反面
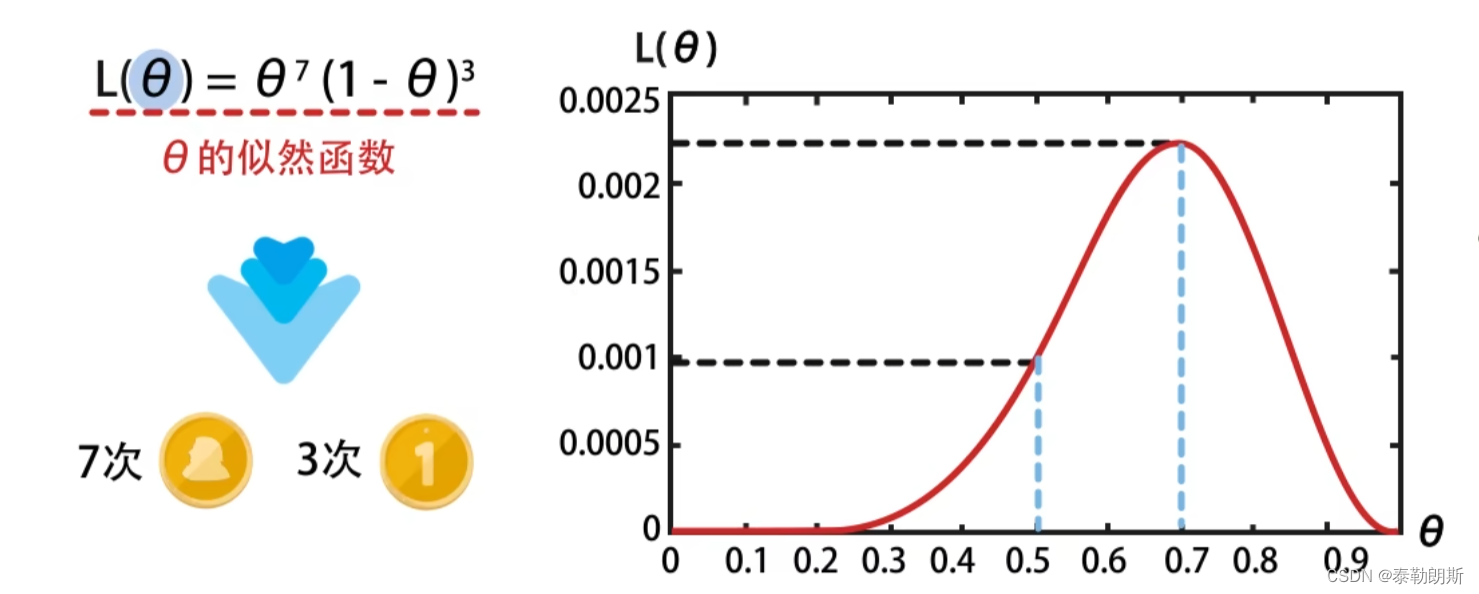
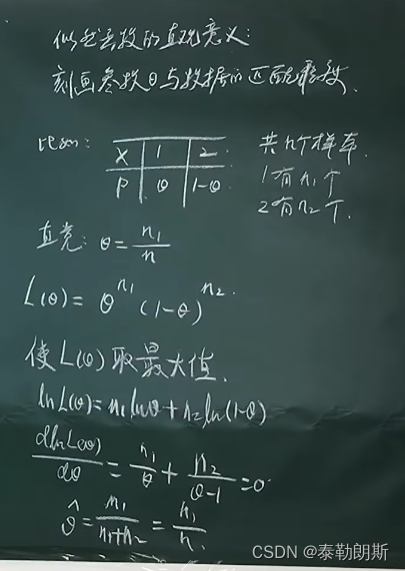
总结
我觉得可以这样理解:
似然函数描述的是当前已经取得的样本的概率分布F,F是 θ \theta θ的函数,因为 θ \theta θ是未知的,所以F的具体值由 θ \theta θ的取值来确定。 那么, θ \theta θ取哪个值才能“最恰当”的描述我们取得的这组样本呢? 因为我只有手头这些样本,既然就这么巧就拿到了这些,我就认为出现手头这些样本的概率是最大的。似然函数描述的是手头这些样本的概率,最大化似然函数 f ( θ ) f(\theta) f(θ),就可以得到 θ \theta θ值了。 关键在于,我们就这么巧,拿到的手头这些样本,那么手头这些样本出现的概率就是最大的, 可以这样理解极大似然!
比如上文中,只有 θ = 0.7 \theta=0.7 θ=0.7的时候, f ( θ ) f(\theta) f(θ)的值最大。
那么这个函数是怎么推导出来的,或者说是谁发现这个函数有这个性质呢?留给你
上面只有两个概率分布,那么多个概率分布呢,比如筛子6个面。
最大熵模型中的对数似然函数的解释
怕你看不懂,解释一下,下面的 x 1 , x 2 , x 3 . . . x_1,x_2,x_3... x1,x2,x3...指的是我们上面筛子中的1-6中的某个点(其余案例阔以按照这个扩散), θ \theta θ 就是出现这个点数的概率。
比如十次,1-6出现的次数依次是,5,1,1,1,1,1
那么最大似然就是:
L p = 0. 5 5 ∗ 0. 1 1 ∗ 0. 1 1 ∗ 0. 1 1 ∗ 0. 1 1 ∗ 0. 1 1 L_p=0.5^5*0.1^1*0.1^1*0.1^1*0.1^1*0.1^1 Lp=0.55∗0.11∗0.11∗0.11∗0.11∗0.11,这样的时候L最大。

相关文章:

似然和概率
前言 高斯在处理正态分布的首次提出似然,后来英国物理学家,费歇尔 概率是抛硬币之前,根据环境推断概率 似然则相反,根据结果推论环境 P是关于x的函数,比如x为正面朝上的结果,或者反面朝上的结果…...

php代码审计篇熊海cms代码审计
文章目录 自动审计逐个分析首页index.php文件包含漏洞后台逻辑漏洞cookie绕过登录后台sql报错注入存储型XSS 结束吧 自动审计 看到有很多 逐个分析 首页index.php文件包含漏洞 读一下代码,可以看到很明显的一个文件包含 <?php //单一入口模式 error_repor…...
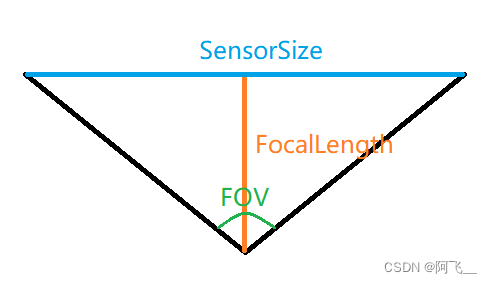
Android Camera2获取摄像头的视场角(FOV)信息
一、概念 FOV(Field of View)是一个用于描述视野范围的术语。它通常用于计算设备(如摄像机、虚拟现实头显或眼睛)所能捕捉到的可见区域。 水平FOV(Horizontal FOV):描述视野在水平方向上的范围…...
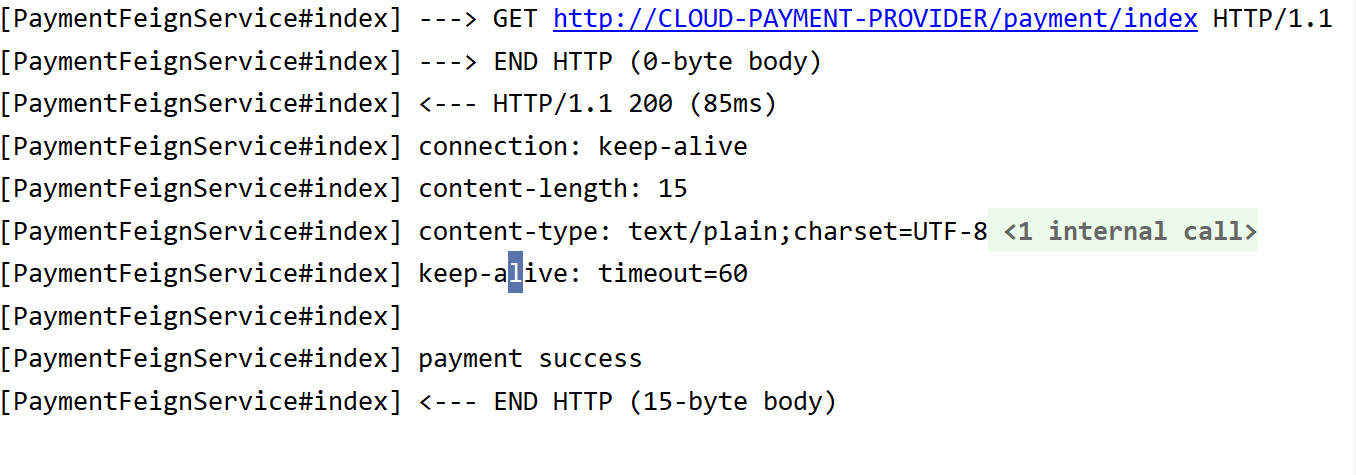
服务接口调用OpenFeign_日志增强
OpenFeign虽然提供了日志增强功能,但是默认是不显示任何日志的,不过开发者在调试阶段可以自己配置日志的级别。 OpenFeign的日志级别如下: NONE:默认的,不显示任何日志;BASIC:仅记录请求方法、URL、响应状…...

ADC数模转化器
简介 • ADC ( Analog-Digital Converter )模拟 - 数字转换器 • ADC 可以将引脚上连续变化的模拟电压转换为内存中存储的数字变量,建立模拟电路到数字电路的桥梁 • 12 位逐次逼近型 ADC , 1us 转换时间 (12位:分辨率…...
Linux DataEase数据可视化分析工具结合cpolar实现远程访问
文章目录 前言1. 安装DataEase2. 本地访问测试3. 安装 cpolar内网穿透软件4. 配置DataEase公网访问地址5. 公网远程访问Data Ease6. 固定Data Ease公网地址 前言 DataEase 是开源的数据可视化分析工具,帮助用户快速分析数据并洞察业务趋势,从而实现业务…...

使用JAXB将xml转成Java对象
文章目录 使用JAXB将xml转成Java对象1. xml内容2. Java对象类3. 封装的工具类4. 测试 使用JAXB将xml转成Java对象 工作中遇到个问题,需要将xml转对象,之前复杂的xml都是自己用dom4j来解析组装成Java对象,但是对于简单的,看到了JAX…...
第6讲:v-for使用
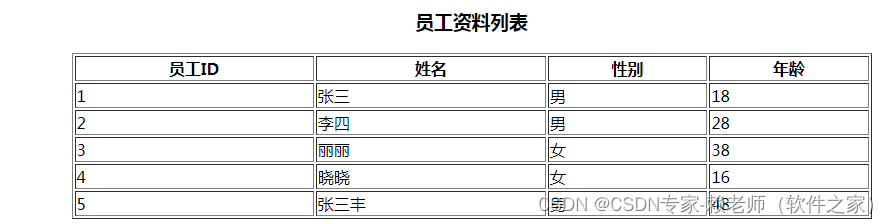
目录 1.循环遍历 2.v-for遍历整形变量(99乘法表) 3.v-for遍历普通数组 4.v-for遍历数组对象 1.循环遍历 v-for指令基于一个数组渲染一个列表,它和JavaScript的遍历语法相似: v-for”item in list” list 是一个数组, i…...

ubuntu http 服务器响应
代码: h文件 #include <iostream> #include <curl/curl.h>#include <net/if.h> #include <sys/ioctl.h> #include <arpa/inet.h> #include <string.h>#include <event.h> #include <event2/http.h> #include <…...

C语言 结构体位域
在C语言中,结构体位域是一种特殊的结构体成员,它允许在结构体中定义一个二进制位字段,以便在单个字节中存储多个布尔值或枚举值。 结构体位域的定义方式如下: struct { unsigned int bit1: 1; // 定义一个名为bit1的位域&…...

ChatGPT AIGC 非常实用的AI工具集合大全
实战AI 工具箱 AIGC ChatGPT 职场案例60集, Power BI 商业智能 68集, 数据库Mysql8.0 54集 数据库Oracle21C 142集, Office, Python ,ETL Excel 2021 实操,函数,图表,大屏可视化 案例实战 http://t.csdn.cn/zBytu...

Visual Studio Cpp CLR C# 替换
1、首先将文件中所有都替换 你需要的名字 替换为整个解决方案 2、新建工程取名 Laserbeam_upper 3、把原工程下的cpp放进来,并改名Laserbeam_upper 4、在这里逐步添加 属性表配置opencv 5、cpp需要修改的两个地方 6、CLR新建和添加 选类库新建、然后直接粘贴进来…...

typeorm利用mongodb,save的时候更新会出现重复数据的问题。
是因为mongodb把new Object当成插入的数据了,修正方案 ObjectIdColumn({name: _id,})Transform((value) > new ObjectId(value.obj._id.toString()))// ts-ignore_id: ObjectId;Transform((value) > new ObjectId(value.obj._id.toString()))转换下就好了。...
决策树案例分析
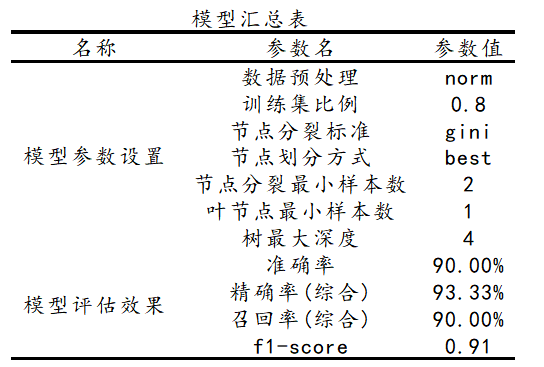
决策树(Decision Tree)常用于研究类别归属和预测关系的模型,比如是否抽烟、是否喝酒、年龄、体重等4项个人特征可能会影响到‘是否患癌症’,上述4项个人特征称作‘特征’,也即自变量(影响因素X),‘是否患癌…...
Linux基本操作符(1)
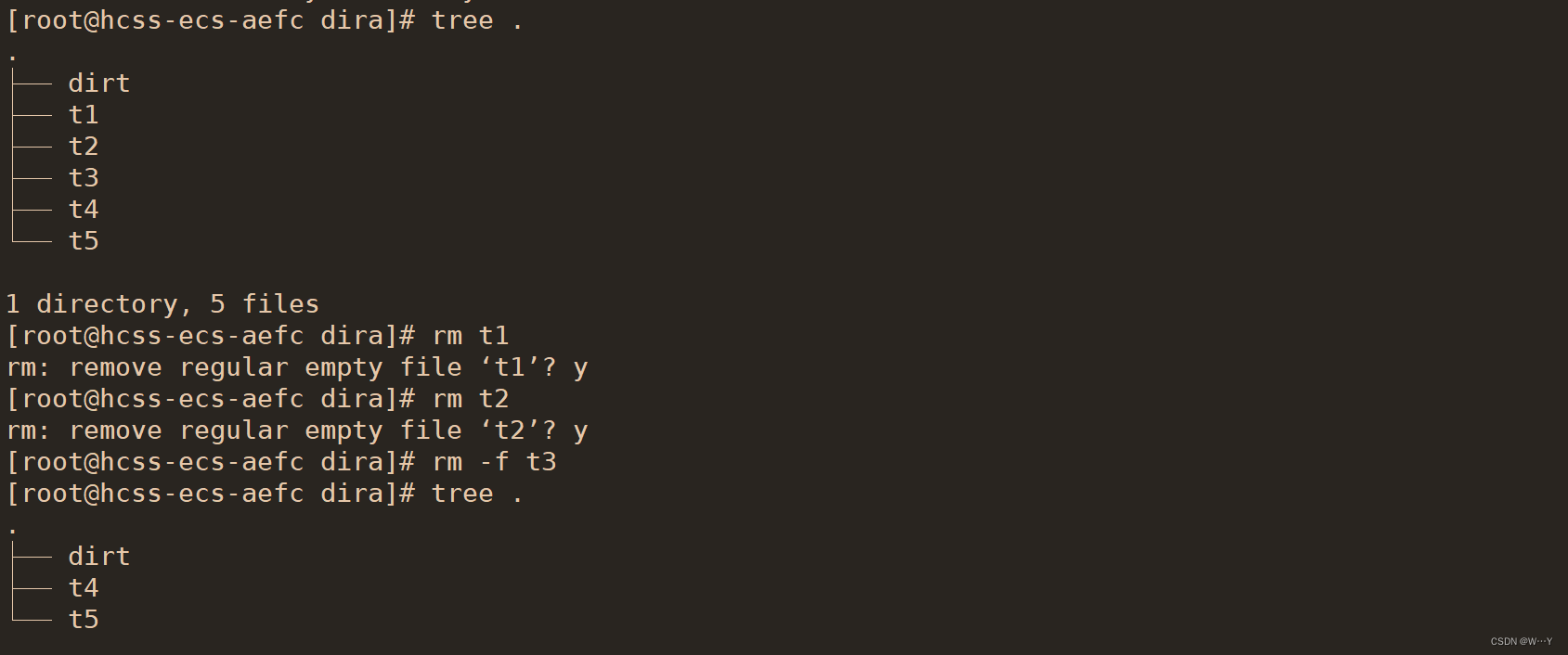
W...Y的主页 😊 代码仓库分享 💕 目录 Linux的登录 Linux下基本指令 指令操作的理解 几个与用户操作符 ls 指令 pwd命令 cd 指令 touch指令 mkdir指令 rmdir指令 && rm 指令 什么叫操作系统,我相信如果是学计算机的都听说过&…...
pg数据表同步到hive表数据压缩总结
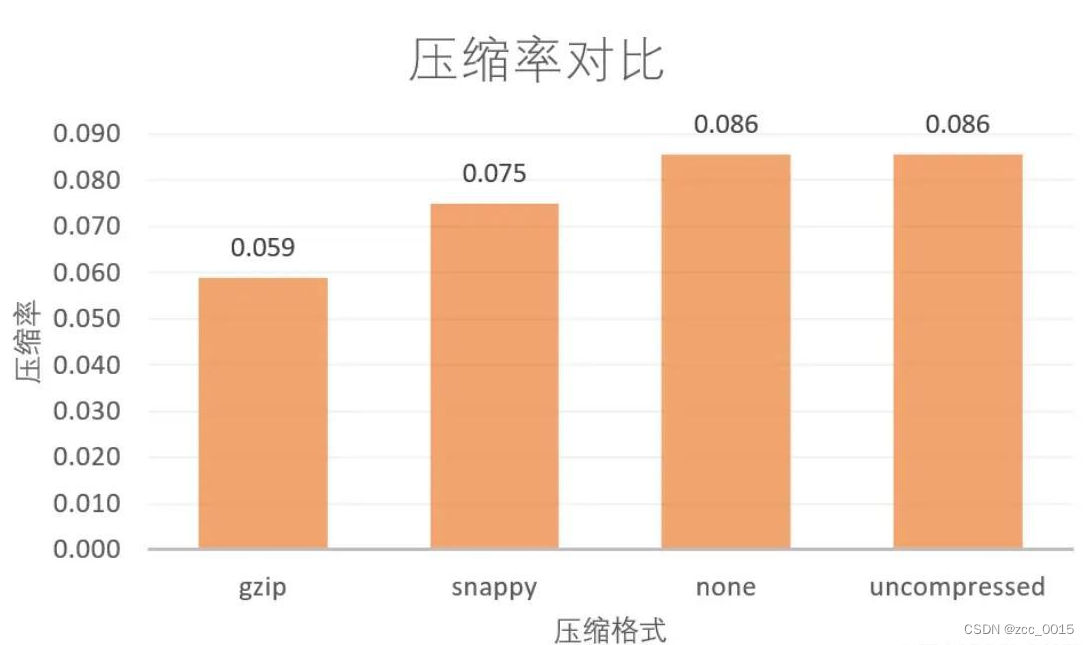
1、背景 pg库存放了大量的历史数据,pg的存储方式比较耗磁盘空间,pg的备份方式,通过pgdump导出后,进行gzip压缩,压缩比大概1/10,随着数据的积累磁盘空间告警。为了解决pg的压力,尝试采用hive数据…...

2023-Chrome插件推荐
Chrome插件推荐 一键管理扩展 链接 https://chromewebstore.google.com/detail/lboblnfejcmcaplhnbkkfcienhlhpnni 介绍 一键开启、禁用Chrome插件。 Checker Plus for Gmail™ 链接 https://jasonsavard.com/zh-CN/Checker-Plus-for-Gmail https://chromewebstore.goo…...
VUE使用DXFParser组件解析dxf文件生成图片
<template><div><input type"file" change"handleFileChange" /></div><el-table :data"tableData" style"width: 100%"><el-table-column prop"Control_No" label"序号" width…...

SpringBoot 集成 AKKA
文章目录 应用场景与 SpringBoot 集成示例 应用场景 AKKA 是一个用于构建高并发、分布式和容错应用程序的开源框架。它基于Actor模型,提供了强大的并发抽象和工具,适用于各种业务场景。以下是一些使用AKKA框架的常见业务场景的示例: 实时数据…...

什么是Service Worker?它在PWA中的作用是什么?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ Service Worker的作用是什么?⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

react-pdf(pdfjs-dist)如何兼容老浏览器(chrome 49)
之前都是使用react-pdf来渲染pdf文件,这次有个需求是要兼容xp环境,xp上chrome最高支持到49,虽然说iframe或者embed都可以实现预览pdf,但为了后续的定制化需求,还是需要使用js库来渲染。 chrome 49测试环境 能用的测试…...
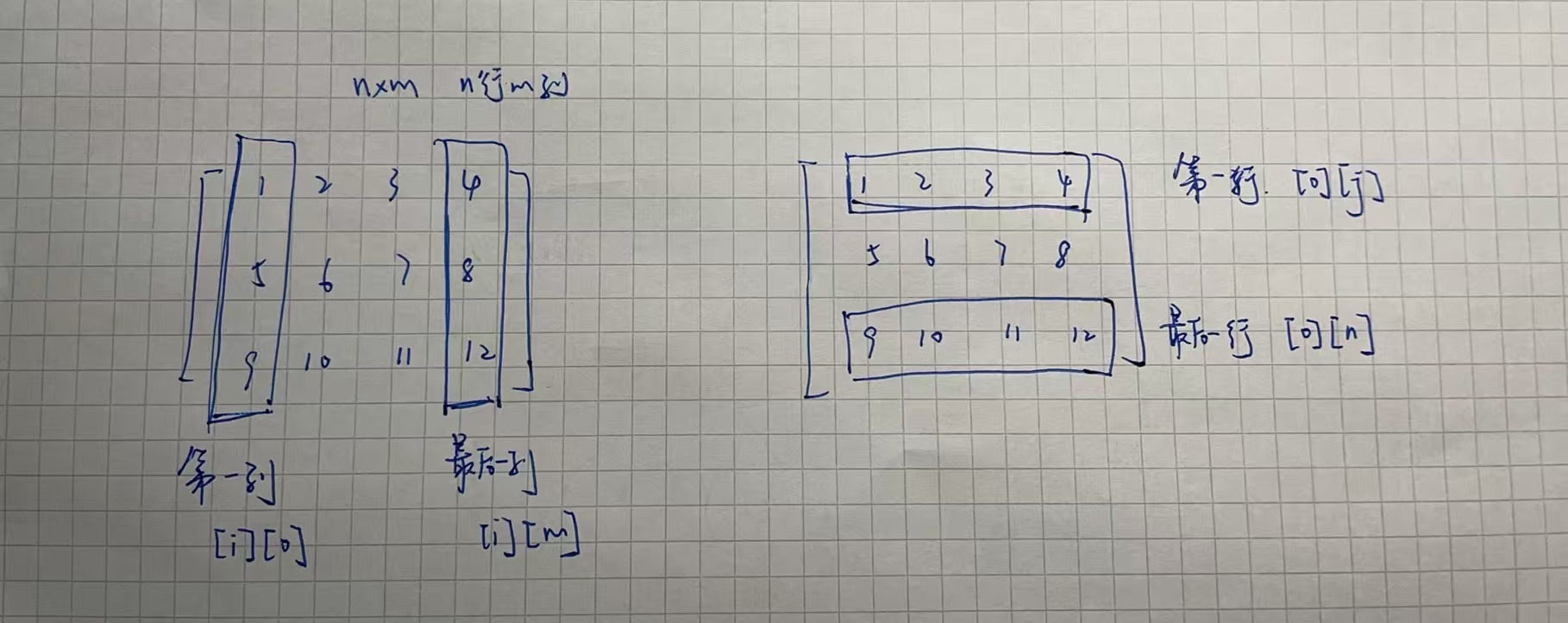
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...
