代码随想录day49:动态规划part10
121.买卖股票的最佳时机
贪心:
class Solution {
public:int maxProfit(vector<int>& prices) {int low = INT_MAX;int result = 0;for (int i = 0; i < prices.size(); i++) {low = min(low, prices[i]); // 取最左最小价格result = max(result, prices[i] - low); // 直接取最大区间利润}return result;}
};动态规划:
1.dp数组的定义–dp[i][0]表示第i天持有股票所得最多现金,dp[i][1]表示第i天不持有股票所得最多现金。注意持有不等于第i天买入。
2.递推公式:
dp[i][0] = max(dp[i - 1][0], -prices[i])第i天持有股票可能是前一天就持有股票,也可能是今天刚买的股票
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);第i天不持有股票可能是昨天卖出的,也可能是今天卖出的。
3.dp数组初始化:其基础都是要从dp[0][0]和dp[0][1]推导出来。
第0天就持有股票,则就是第0天买入的。dp[0][0]=-price[0];
第0天不持有股票,则还没开始买股票,dp[0][1]=0;
4.遍历顺序:从前向后遍历。
class Solution {
public:int maxProfit(vector<int>& prices) {vector<vector<int>> dp(prices.size(),vector<int>(2,0));dp[0][0]=-prices[0];dp[0][1]=0;for(int i=1;i<prices.size();i++){dp[i][0]=max(dp[i-1][0],-prices[i]);//dp[i-1][1]-pricesdp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]);}return dp[prices.size()-1][1];}
};
优化:从递推公式可以看出,dp[i]只是依赖于dp[i - 1]的状态。那么我们只需要记录 当前天的dp状态和前一天的dp状态就可以了,可以使用滚动数组来节省空间:
class Solution {
public:int maxProfit(vector<int>& prices) {vector<vector<int>> dp(2,vector<int>(2,0));dp[0][0]=-prices[0];dp[0][1]=0;for(int i=1;i<prices.size();i++){dp[i%2][0]=max(dp[(i-1)%2][0],-prices[i]);//dp[i-1][1]-pricesdp[i%2][1]=max(dp[(i-1)%2][1],dp[(i-1)%2][0]+prices[i]);}return dp[(prices.size()-1)%2][1];}
};
买卖股票的最佳时机II
与上一道题的区别:可以多次买卖一支股票,但必须在再次购买前出售掉之前的股票
之前的贪心算法就用的这个例子讲的
 这次动态规划的方法:
这次动态规划的方法:
1.dp数组的定义:dp[i][0] 表示第i天持有股票所得现金。dp[i][1] 表示第i天不持有股票所得最多现金
2.递推公式:
dp[i][0] = max(dp[i - 1][0], dp[i-1][1]-prices[i])第i天持有股票可能是前一天就持有股票,也可能是今天刚买的股票
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);第i天不持有股票可能是昨天卖出的,也可能是今天卖出的。
3.dp数组初始化:其基础都是要从dp[0][0]和dp[0][1]推导出来。
第0天就持有股票,则就是第0天买入的。dp[0][0]=-price[0];
第0天不持有股票,则还没开始买股票,dp[0][1]=0;
4.遍历顺序:从前向后遍历。
vector<vector<int>> dp(2,vector<int>(2,0));dp[0][0]=-prices[0];dp[0][1]=0;for(int i=1;i<prices.size();i++){dp[i%2][0]=max(dp[(i-1)%2][0],dp[(i-1)%2][1]-prices[i]);//dp[i-1][1]-pricesdp[i%2][1]=max(dp[(i-1)%2][1],dp[(i-1)%2][0]+prices[i]);}return dp[(prices.size()-1)%2][1];
相关文章:

代码随想录day49:动态规划part10
121.买卖股票的最佳时机 贪心: class Solution { public:int maxProfit(vector<int>& prices) {int low INT_MAX;int result 0;for (int i 0; i < prices.size(); i) {low min(low, prices[i]); // 取最左最小价格result max(result, prices[i…...

fofa搜索使用
fofa搜索使用 文章目录 fofa搜索使用网站fofa搜索语法多条件查询 网站fofa https://fofa.info/搜索语法 1.title”beijing”从标题中搜索“北京2.headerQ"thinkphp”从http响应头中搜索“thinkphp3.body”管理后台”从html正文中搜索“管理后台4.domain”163.com”从子域…...

husky+lint-staged+eslint+prettier+stylelint+commitlint
概念: husky,暴露出git的hook钩子,在这些钩子执行一些命令,lint-staged,只在git的暂存区有修改的文件进行lint操作,执行一些校验脚本eslint,prettier,styelint有npm包还有对应的scode插件,其中npm包是用于执行那些诸如入eslint --fix "src/**/*.{js,jsx,…}"的脚本命…...

图像处理与计算机视觉--第四章-图像滤波与增强-第一部分
目录 1.灰度图亮度调整 2.图像模板匹配 3.图像裁剪处理 4.图像旋转处理 5.图像邻域与数据块处理 学习计算机视觉方向的几条经验: 1.学习计算机视觉一定不能操之过急,不然往往事倍功半! 2.静下心来,理解每一个函数/算法的过程和精髓&…...

【go】字符串切片与字符串出入数据库转化
文章目录 需求代码入库出库 需求 将请求数据存入数据库与从数据库读取数据返回在出库不使用反序列化情况下 请求结构体 type NoticegroupsCreateReq struct {Name string json:"name" binding:"required"UserIds []string json:"user_ids…...
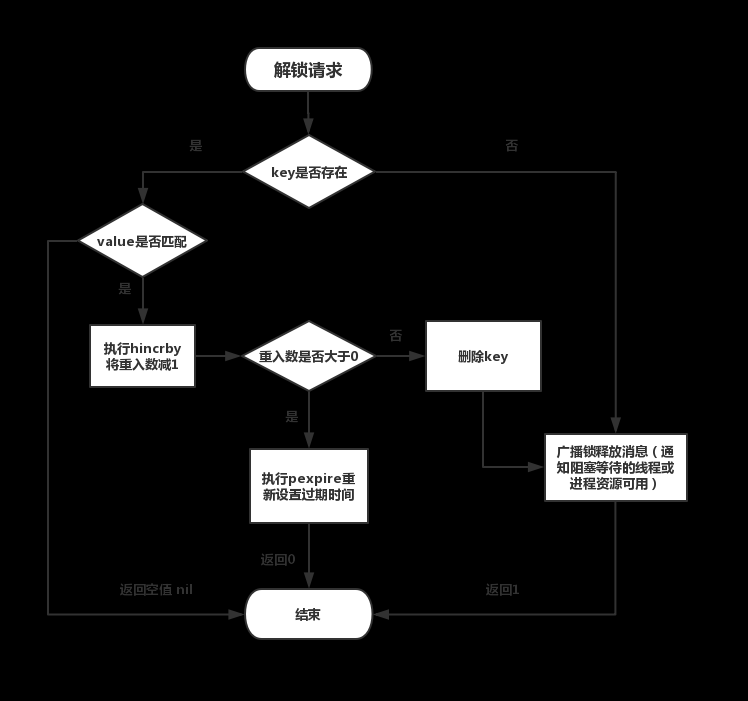
Redis中是如何实现分布式锁的?
分布式锁常见的三种实现方式: 数据库乐观锁; 基于Redis的分布式锁; 基于ZooKeeper的分布式锁。 本次面试考点是,你对Redis使用熟悉吗?Redis中是如何实现分布式锁的。 要点 Redis要实现分布式锁,以下条件应…...

似然和概率
前言 高斯在处理正态分布的首次提出似然,后来英国物理学家,费歇尔 概率是抛硬币之前,根据环境推断概率 似然则相反,根据结果推论环境 P是关于x的函数,比如x为正面朝上的结果,或者反面朝上的结果…...

php代码审计篇熊海cms代码审计
文章目录 自动审计逐个分析首页index.php文件包含漏洞后台逻辑漏洞cookie绕过登录后台sql报错注入存储型XSS 结束吧 自动审计 看到有很多 逐个分析 首页index.php文件包含漏洞 读一下代码,可以看到很明显的一个文件包含 <?php //单一入口模式 error_repor…...
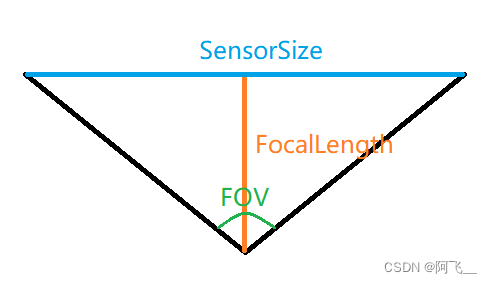
Android Camera2获取摄像头的视场角(FOV)信息
一、概念 FOV(Field of View)是一个用于描述视野范围的术语。它通常用于计算设备(如摄像机、虚拟现实头显或眼睛)所能捕捉到的可见区域。 水平FOV(Horizontal FOV):描述视野在水平方向上的范围…...
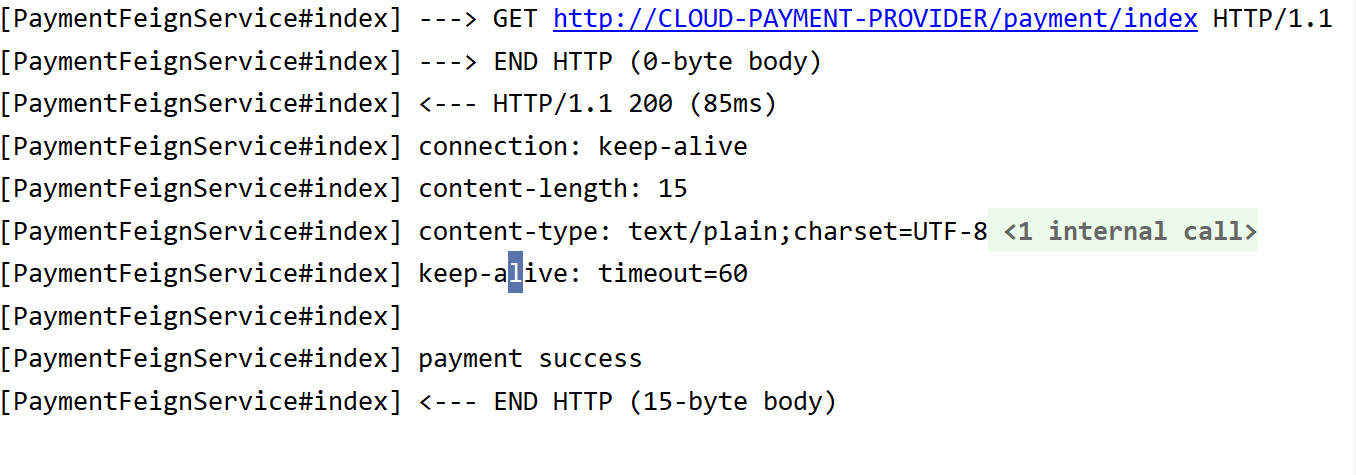
服务接口调用OpenFeign_日志增强
OpenFeign虽然提供了日志增强功能,但是默认是不显示任何日志的,不过开发者在调试阶段可以自己配置日志的级别。 OpenFeign的日志级别如下: NONE:默认的,不显示任何日志;BASIC:仅记录请求方法、URL、响应状…...

ADC数模转化器
简介 • ADC ( Analog-Digital Converter )模拟 - 数字转换器 • ADC 可以将引脚上连续变化的模拟电压转换为内存中存储的数字变量,建立模拟电路到数字电路的桥梁 • 12 位逐次逼近型 ADC , 1us 转换时间 (12位:分辨率…...
Linux DataEase数据可视化分析工具结合cpolar实现远程访问
文章目录 前言1. 安装DataEase2. 本地访问测试3. 安装 cpolar内网穿透软件4. 配置DataEase公网访问地址5. 公网远程访问Data Ease6. 固定Data Ease公网地址 前言 DataEase 是开源的数据可视化分析工具,帮助用户快速分析数据并洞察业务趋势,从而实现业务…...

使用JAXB将xml转成Java对象
文章目录 使用JAXB将xml转成Java对象1. xml内容2. Java对象类3. 封装的工具类4. 测试 使用JAXB将xml转成Java对象 工作中遇到个问题,需要将xml转对象,之前复杂的xml都是自己用dom4j来解析组装成Java对象,但是对于简单的,看到了JAX…...
第6讲:v-for使用
目录 1.循环遍历 2.v-for遍历整形变量(99乘法表) 3.v-for遍历普通数组 4.v-for遍历数组对象 1.循环遍历 v-for指令基于一个数组渲染一个列表,它和JavaScript的遍历语法相似: v-for”item in list” list 是一个数组, i…...

ubuntu http 服务器响应
代码: h文件 #include <iostream> #include <curl/curl.h>#include <net/if.h> #include <sys/ioctl.h> #include <arpa/inet.h> #include <string.h>#include <event.h> #include <event2/http.h> #include <…...

C语言 结构体位域
在C语言中,结构体位域是一种特殊的结构体成员,它允许在结构体中定义一个二进制位字段,以便在单个字节中存储多个布尔值或枚举值。 结构体位域的定义方式如下: struct { unsigned int bit1: 1; // 定义一个名为bit1的位域&…...

ChatGPT AIGC 非常实用的AI工具集合大全
实战AI 工具箱 AIGC ChatGPT 职场案例60集, Power BI 商业智能 68集, 数据库Mysql8.0 54集 数据库Oracle21C 142集, Office, Python ,ETL Excel 2021 实操,函数,图表,大屏可视化 案例实战 http://t.csdn.cn/zBytu...

Visual Studio Cpp CLR C# 替换
1、首先将文件中所有都替换 你需要的名字 替换为整个解决方案 2、新建工程取名 Laserbeam_upper 3、把原工程下的cpp放进来,并改名Laserbeam_upper 4、在这里逐步添加 属性表配置opencv 5、cpp需要修改的两个地方 6、CLR新建和添加 选类库新建、然后直接粘贴进来…...

typeorm利用mongodb,save的时候更新会出现重复数据的问题。
是因为mongodb把new Object当成插入的数据了,修正方案 ObjectIdColumn({name: _id,})Transform((value) > new ObjectId(value.obj._id.toString()))// ts-ignore_id: ObjectId;Transform((value) > new ObjectId(value.obj._id.toString()))转换下就好了。...
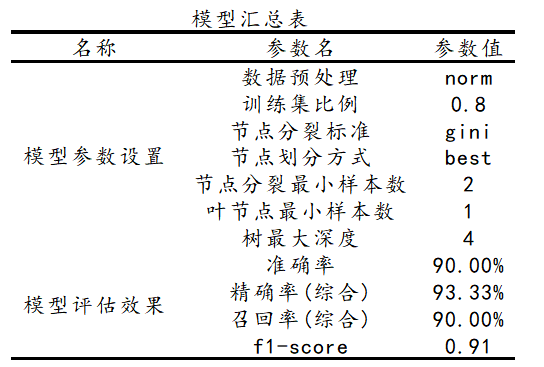
决策树案例分析
决策树(Decision Tree)常用于研究类别归属和预测关系的模型,比如是否抽烟、是否喝酒、年龄、体重等4项个人特征可能会影响到‘是否患癌症’,上述4项个人特征称作‘特征’,也即自变量(影响因素X),‘是否患癌…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
