KMP算法详细理解
一、目的
1.KMP应用场景:可以解决字符串匹配问题; 在一个串中查找是否出现过另一个串。
2.KMP的经典思想就是:当出现字符串不匹配时,可以记录一部分之前已经匹配的文本内容,利用这些信息避免从头再去做匹配。
3.KMP算法关键在于:在当前对文本串和模式串检索的过程中,若出现了不匹配,如何充分利用已经匹配的部分。
4.理解KMP需要搞懂的几个方面:
什么是前缀表?为什么一定要用前缀表?如何计算前缀表
前缀表与next数组关系?构造next数组的几种方法?
如何使用next数组来做匹配
二、理解过程
1.例子:用模式串去匹配文本串
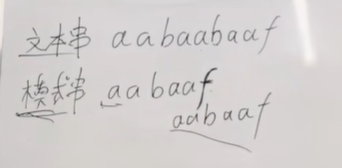

(1)暴力破解:O(m+n)
(2)KMP算法:先进行常规匹配,到b和f不相等时,会直接将f移动到b的位置来匹配(因为b前面的两个a已经匹配好了),直至匹配完成。
2.前缀表:用来回退的,它记录了模式串与主串(文本串)不匹配时,模式串应该从哪里开始重新匹配。
(1)学会找最长相等前后缀(关键!!)
(2)前缀:包含首字母,不包含尾字母的所有子串
eg.例子里的前缀有a,aa,aab,aaba,aabaa。 aabaaf就不是前缀即不可以包含尾字母
同理后缀:f.af.aaf.baaf.abaaf
(3)什么是最长相等前后缀?
答:前缀=后缀且最长
过程:找模式串的最长相等前后缀也就是前缀表,利用前缀找最长相等前后缀:
a 0 (a既是前缀又是后缀,所以为0)
aa 1 (前一个a是前缀,后一个a是后缀,且都是a,则长度为1)
aab 0 (前缀有a,aa,后缀有b,ab,整个来讲找的就是前缀的前缀,前缀的后缀)
aaba 1 (第一个a和b后的a相等)
aabaa 2 (第一个a和最后的a;前aa和后aa)
aabaaf 0
从而得到前缀表为:010120

从图中可知,从第一个a开始匹配,发现到模式串f时匹配不成功,随即立马找f之前的串即aabaa的最长相等前后缀,也就是2,所以就从模式串位置2即第三个数开始重新匹配.
3.next数组:可以理解就是前缀表,但next数组写法很多
(1)其他写法
原始 0 1 0 1 2 0
整体右移 -1 0 1 0 1 2
整体减1 -1 0 -1 0 1 -1
但这里还是用原始的进行操作和编码
4.代码实现(也就是找最长相等前后缀的过程):
步骤:(1)初始化next数组和变量(2)处理前后缀不同的情况(3)处理前后缀相同的情况
(4)更新next
i代表后缀末尾; j指向前缀末尾,也代表包括i之前的最长相等前后缀的长度; 下面是代码和运行过程图
代码是伪代码,不完整:
public void getnext(int[] next, String s){
// 初始化j next;
j = 0, next[0] = j,
for(i = 1; i<s.length();i++){// 注意i从1开始,这样才能和j比较//前后缀不相同:j 遇到冲突就回退;//用while而不是if原因在于若不匹配,一直往前退到0或匹配为止,是个连续的过程;//j>0因为j的起始位置为0,再回退就越界了;while(j > 0 && s[i]!=s[j] ){j = next[j-1]; }// 向前回溯,回溯前一位的next中的位置//前后缀相同 if(s[i]==s[j]) j++; 最长相等前后缀长度加1next[i] = j; }//将j(前缀的长度)赋给next【i】,不管前后缀是否相同,都要存放例题实现strStr() ①先对模式串进行kmp,得到next数组即前缀表

②将文本串和模式串进行匹配,使用next数组保存的最长相等前后缀辅助。

相关文章:

KMP算法详细理解
一、目的1.KMP应用场景:可以解决字符串匹配问题; 在一个串中查找是否出现过另一个串。2.KMP的经典思想就是:当出现字符串不匹配时,可以记录一部分之前已经匹配的文本内容,利用这些信息避免从头再去做匹配。3.KMP算法关键在于&…...

RabbitMQ单节点安装
在学习RabbitMQ之前,必须要把RabbitMQ的环境搭建起来,刚开始学习时,搭建单节点是入门RabbitMQ最方便、最快捷的方式,这篇文章就是介绍如何使用RabbitMQ压缩包的方式搭建一个单节点的RabbitMQ。 在实际项目中,服务器都…...

tomcat 服务的目录结构和tomcat的运行模式
目录 一、tomcat 服务的目录结构解析: 1、tomcat目录结构: bin目录: conf目录: lib目录: logs目录: temp目录: webapps目录: wokr目录: 二、tomcat服务的运行模…...
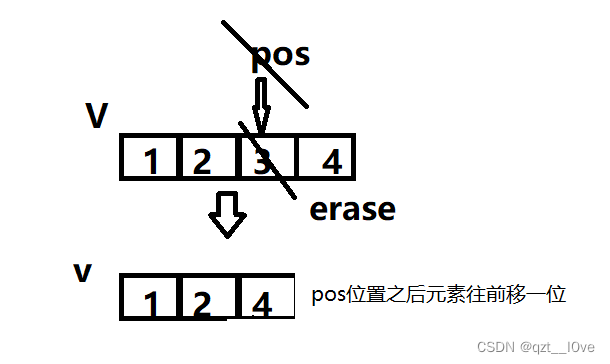
vector迭代器失效问题
一、迭代器: 迭代器的主要作用就是让算法能够不用关心底层数据结构,其底层实际就是一个指针,或者是对指针进行了封装,比如:vector的迭代器就是原生态指针T* 。因此迭代器失效,实际就是迭代器底层对应指针所…...

2023年排名前茅的十大饭店装修设计!
相信大家都是知道的,饭店装修设计其实是一门很深的学问,只有掌握这门学问才能够打造出来精美的空间,因此饭店装修必须要有专业餐饮设计公司的设计师进行设计。但是在国内饭店装修设计公司那么多,饭店老板要如何选择呢?…...
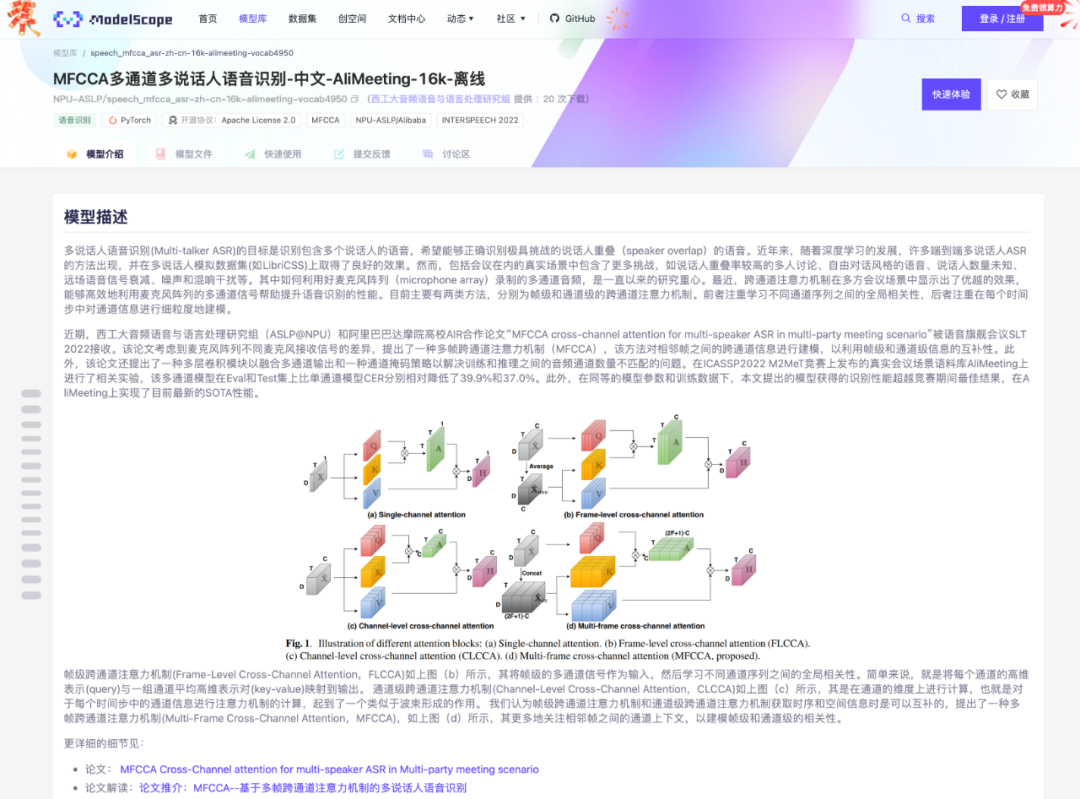
MFCCA多通道多说话人语音识别模型上线魔搭(ModelScope)
实验室研发的基于多帧跨通道注意力机制(MFCCA)的多说话人语音识别模型近日上线魔搭(ModelScope)社区,该模型在AliMeeting会议数据集上获得当前最优性能。欢迎大家下载。开发者可以基于此模型进一步利用ModelScope的微调…...

刷题记录:牛客NC25078[USACO 2007 Ope S]City Horizon
传送门:牛客 题目描述: Farmer John has taken his cows on a trip to the city! As the sun sets, the cows gaze at the city horizon and observe the beautiful silhouettes formed by the rectangular buildings. The entire horizon is represented by a number line …...

【Java|golang】 1238. 循环码排列---格雷编码
给你两个整数 n 和 start。你的任务是返回任意 (0,1,2,…,2^n-1) 的排列 p,并且满足: p[0] start p[i] 和 p[i1] 的二进制表示形式只有一位不同 p[0] 和 p[2^n -1] 的二进制表示形式也只有一位不同 示例 1: 输入:n 2, start …...

Python自动化测试框架封装和调用
封装与调用函数与参数化前言 面实现了参数的关联,那种只是记流水账的完成功能,不便于维护,也没什么可读性,接下来这篇可以把每一个动作写成一个函数,这样更方便了。参数化的思维只需记住一点:不要写死 登录…...
线程的执行
承接上文CPU原理简介程序的执行是由控制器发信号推动整个程序一步一步向前走,将数据存储在寄存器,从程序计数器中获取指令,比如先把3放到寄存器,再把5放到寄存器,再做一个加法,加法就是一个指令,…...

【视频】海康摄像头、NVR网络协议简介
1、软硬件整体架构 2、涉及的网络协议 3、协议简介 3.1 海康私有协议 设备发现SADP:进行设备的发现、激活、修改网络参数、忘记密码等; SDK:4200、系统平台的接入前端设备,协议不对外开放,但对外提供接口库; ISAPI:Intelligent Security API(智能安全API),基于HTTP传输…...

【Spring的事务传播行为有哪些呢?Spring事务的隔离级别?讲下嵌套事务?】
如果你想寻求一份与后端相关的开发工作,那么关于Spring事务相关的面试题你就不能说不会并且不能不知道? 人生如棋,我愿为卒,行动虽慢,可谁曾见我后退一步? 一.Spring中声明事务的方式 1.1 编程式事务 编程…...

其实一点不难学会这三步一定让你学会制作一个『3D建模』大屏
上次已经教过大家怎样制作一个简单的2D数据可视化大屏~那有一些朋友们就会说那些炫酷的3D可视化大屏是怎样制作的呢?这不就来了,今天就教大家怎样用山海鲸可视化软件制作一个带3D建模的可视化大屏,并且最重要的是无需会特别复杂的3D建模知识。…...
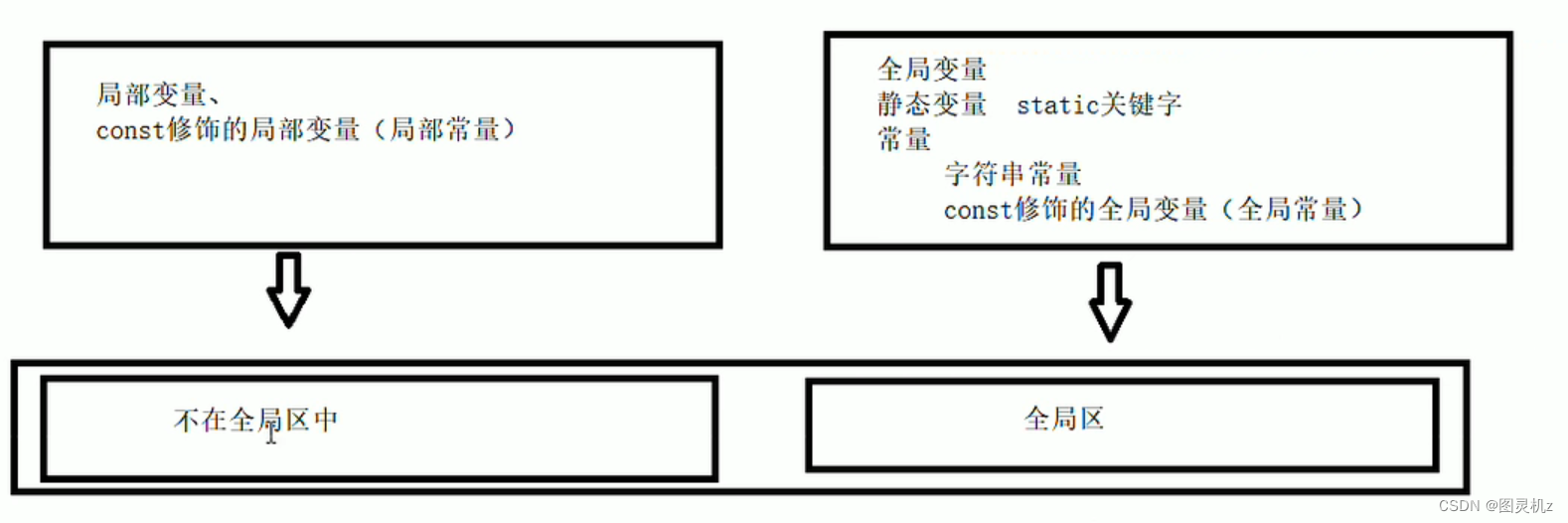
【C++】C++的内存模型之四大分区
程序的内存模型 C程序在执行时,将内存大方向划分为4个区域 代码区:存放函数体的二进制代码,由操作系统进行管理的全局区:存放全局变量和静态变量以及常量栈区:由编译器自动分配释放,存放函数的参数值&…...

Vue跨级通信(重点)
当不使用Vuex的前提下,子孙传递就得使用另外一种办法:provide 和 inject 总结:provide / inject 类似于消息的订阅和发布。- inject接收数据。- provide提供或发送数据,(1)provide(name…...

支付系统中的设计模式07:责任链模式
最近公司业务的发展果然如老板当初所画(预)饼(言)的那样红(恍)红(恍)火(惚)火(惚),蒸蒸日上,每天的流水都在不断攀升到新的高度,有不少人都从公司开发的电商平台挣到了钱。 不过问题也接着来了——运营部门经过老板的同意,也学着产品经理提出了下面几项非常合理…...

期末综合考试
一、概率论1、全概率公式、贝叶斯公式应用2、期望、方差、协方差的定义以及性质证明(1) 期望(2) 方差(3) 协方差二、数理统计1、参数估计(1) 矩估计(2) 最大似然估计(3) 综合例题一、概率论 1、全概率公式、贝叶斯公式应用 记住标黄的两段,上考场直接套数据&#x…...
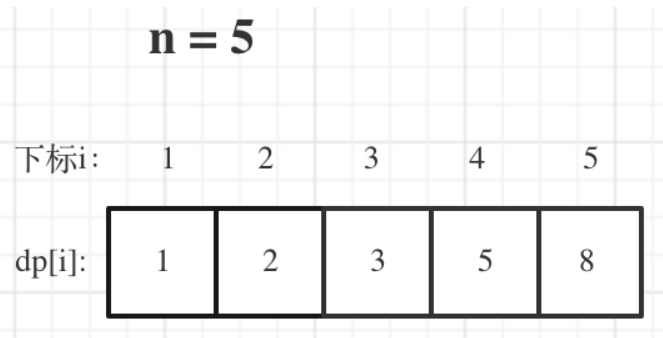
数据结构与算法之爬楼梯动态规划
一.题目(爬楼梯)假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?注意:给定 n 是一个正整数。示例 1:输入: 2输出: 2解释: 有两种方法可以爬…...
CleanMyMac4.12最新Mac电脑系统垃圾清理神器
CleanMyMac是Mac一款神器,特别是清理已卸载软件残留垃圾文件信息库比较全面。 clearmymac以极其快速和时尚的方式为您提供及时的建议,组织,更新和保护您的Mac。完全支持macOS 11(Big Sur)操作系统;它以其简…...

数据治理如何做?火山引擎 DataLeap 帮助这款产品 3 个月降低计算成本 20%
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 本文讲述字节跳动一款 App 产品的数据治理故事。该产品随着用户体量和数据体量不断增长,数仓的任务量、数据量也不断攀升,运维难、成本贵、稳…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
