笔试强训Day3
学了一坤时Linux,赶紧来俩道题目放松放松。
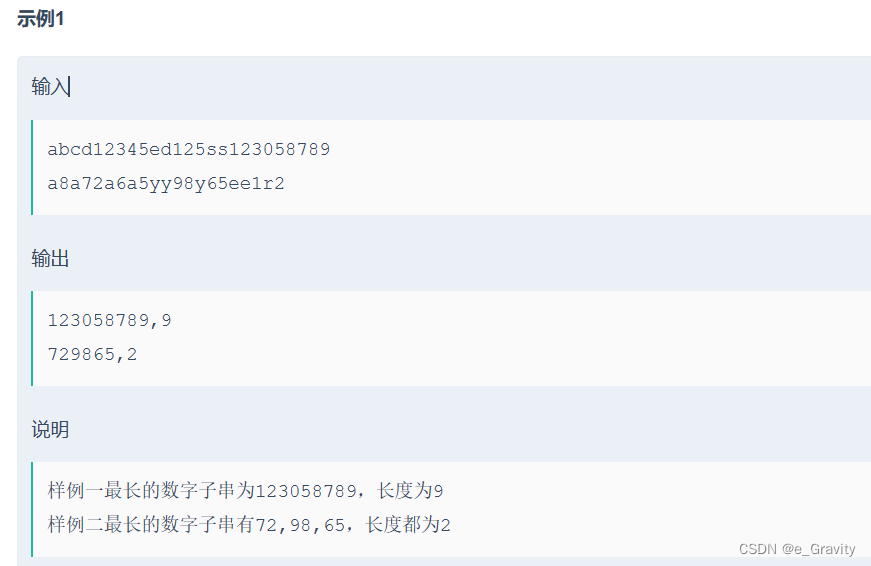
T1:在字符串中找出连续最长的数字串
链接:在字符串中找出连续最长的数字串__牛客网
输入一个字符串,返回其最长的数字子串,以及其长度。若有多个最长的数字子串,则将它们全部输出(按原字符串的相对位置)
本题含有多组样例输入。
数据范围:字符串长度 1≤n≤200, 保证每组输入都至少含有一个数字

这题复刻了一道经典dp【力扣53.最大子数组和】,下面是dp的代码
#include<iostream>
#include<string>
#include<vector>
using namespace std;
string s;
int main()
{while(cin>>s){int ans=0;int n=s.size();int cnt=0;string temp;string res;vector<int>dp(n);if(s[0]>='0'&&s[0]<='9') {dp[0]=1;temp+=s[0];}for(int i=1;i<n;i++){if(s[i]>='0'&&s[i]<='9'){dp[i]=dp[i-1]+1;temp+=s[i];}else{dp[i]=0;temp="";}if(dp[i]>ans){res=temp;}else if(dp[i]==ans){res+=temp;}ans=max(ans,dp[i]);}cout<<res<<","<<ans<<endl;}return 0;
}
其实dp数组可以用一个变量代替,代码会更简洁。
#include<iostream>
#include<string>
using namespace std;
string s;
int main()
{while(cin>>s){int ans=0;int n=s.size();int cnt=0;string temp;string res;for(int i=0;i<n;i++){if(s[i]>='0'&&s[i]<='9'){cnt++;temp+=s[i];}else{cnt=0;temp="";}if(cnt>ans){res=temp;}else if(cnt==ans){res+=temp;}ans=max(ans,cnt);}cout<<res<<","<<ans<<endl;}return 0;
}
T2:数组中出现次数超过一半的数字
链接:数组中出现次数超过一半的数字__牛客网
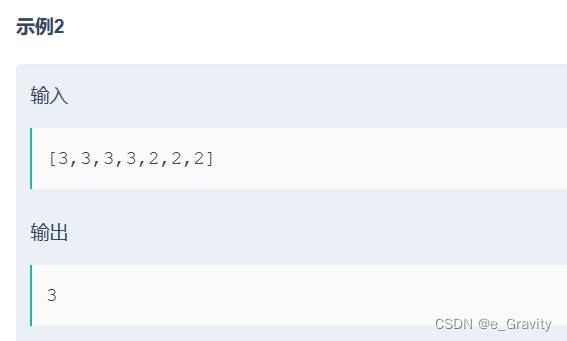
给一个长度为 n 的数组,数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
例如输入一个长度为9的数组[1,2,3,2,2,2,5,4,2]。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。
数据范围:n≤50000,数组中元素的值 0≤val≤100000
要求:空间复杂度:O(1),时间复杂度 O(n)
emmm,开始看道这题,容易想到map一遍,但这题的空间复杂度要求是O(1)。
想了用位运算,不过那些是跟奇偶性有关。
如何数组中存在众数,那众数的数量一定大于数组长度的一半。
我们可以用一种消去的思想:比较相邻的俩个数,如果不相等就消去。最坏的情况下,每次都消去一个众数和一个非众数,如果众数存在,那最后留下的一定就是众数。
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param numbers int整型vector * @return int整型*/int MoreThanHalfNum_Solution(vector<int>& numbers) {// write code hereint cnt=0;int ans=0;int n=numbers.size();for(auto x:numbers){if(!cnt){cnt=1;ans=x;}else{if(ans==x)cnt++;else cnt--;}}cnt=0;for(auto x:numbers){if(x==ans)cnt++;}if(cnt>n/2)return ans;return 0;}
};相关文章:

笔试强训Day3
学了一坤时Linux,赶紧来俩道题目放松放松。 T1:在字符串中找出连续最长的数字串 链接:在字符串中找出连续最长的数字串__牛客网 输入一个字符串,返回其最长的数字子串,以及其长度。若有多个最长的数字子串,…...

软考软件设计师-存储管理-文件管理-计算机网络(中
文章目录 一、存储管理页面置换算法 (最佳OPT)存储页面-先进先出置换算法(FIFO)最久未使用算法(最近最久未使用LRU) 二、文件管理初识文件管理文件目录-绝对路径文件管理-文件的结构文件管理-索引的分配 空闲存储空间的管理(位示图法)三、计算…...

Vue3的学习
create-vue创建vue3项目 create-vue是官方新的脚手架工具,底层切换到了vite(下一代构建工具),为开发提供急速响应 前提环境条件:控制面板输入node -v,显示的是安装了16.0或更高版本的Node.js创建一个Vue应…...
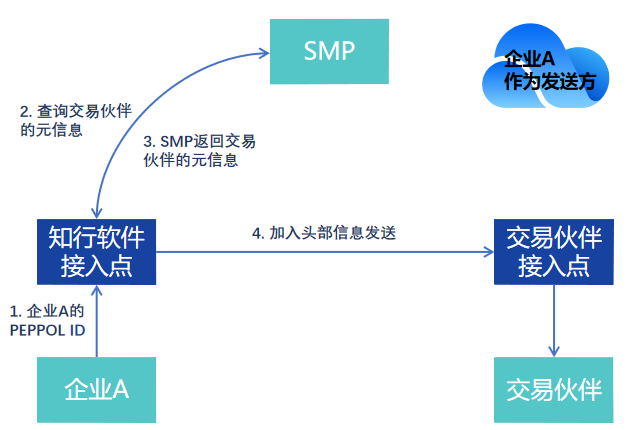
什么是Peppol ID?如何创建?
Peppol 网络的两大优势是安全和高效,由于Peppol 最常用于电子发票,因此这些优势在电子发票上展露无遗。相比之下,通过电子邮件发送 PDF 格式的发票和其他文件不仅处理成本较高,而且容易出现发票欺诈。 如果您所在的公共部门组织或…...

Spring注解大揭秘:@Component、@Service、@Repository详解
Spring注解大揭秘:Component、Service、Repository详解 前言比较 前言 想象一下,你正在构建一个复杂的Spring应用程序。你需要管理各种不同类型的组件,包括服务层、数据访问层和通用组件。Spring的Component、Service和Repository注解就像是你…...

Innodb底层原理与Mysql日志机制
MySQL内部组件结构 Server层 主要包括连接器、词法分析器、优化器、执行器等,涵盖 MySQL 的大多数核心服务功能,以及所有的内置函数(如日期、时间、数学和加密函数等),所有跨存储引擎的功能都在这一层实现,…...

浅谈大数据背景下用户侧用电数据在电力系统的应用与发展分析
安科瑞 华楠 摘要:随着能源互联网、互联网、新型传感技术的持续推进,电力用户侧用电数据呈现指数级剧增、异构性增强的情况,逐渐构成了用户侧用电行为大数据。然而目前对电力领域的数据价值挖掘于电网内部和电源端,用户侧庞大且蕴…...

20230919在WIN10下使用python3将PDF文档转为DOCX格式的WORD文档
20230919在WIN10下使用python3将PDF文档转为DOCX格式的WORD文档 2023/9/19 11:20 python pdf word https://blog.csdn.net/u013185349/article/details/130059657 Python实现PDF转Word文档 AcceptedLin 已于 2023-04-10 14:45:17 修改 1243 收藏 1 文章标签: pd…...

PCR检测试剂——博迈伦
PCR(聚合酶链式反应)是一种常用的分子生物学技术,被广泛应用于基因分型、基因表达分析、病原体检测等领域。在PCR实验中,PCR检测试剂是必不可少的重要组成部分,它们包括引物、酶、缓冲液和核苷酸。 1. 引物(…...
spring一个项目多个模块聚合打包问题解决方案
文章目录 1.问题描述:2.解决方案一、创建聚合父工程二、创建子模块(module)三、编写子模块代码1.模块1(demo-one)2.模块2(demo-tow) 四、创建聚合模块 (demo-starter)1. …...
何时被解析)
Linux设备树(Device Tree)何时被解析
Linux设备树(Device Tree)是在内核启动阶段就会被解析。当 Linux 内核启动的时候,它会读取设备树文件(dtb文件)并根据里面的信息来组织设备、加载驱动等。在驱动代码里,通常我们是在驱动初始化(…...
)
【Elasticsearch】数据简单操作(二)
简介:Elasticsearch(ES)是一个开源的分布式搜索和分析引擎,用于快速存储、搜索和分析大量数据。它具有高性能、可扩展性和灵活性的特点,被广泛用于构建实时搜索、日志分析、数据可视化等应用。 本文主要介绍ES索引的操…...

4 vCPU 实例达成 100 万 JSON API 请求/秒的优化实践
“性能工程” (Performance engineering)是个日渐流行的概念。顾名思义“性能工程”是包含在系统开发生命周期中所应用的一个技术分支,其目的就是确保满足非功能性的性能需求,例如:性能、可靠性等。由于现代软件系统变…...

呼叫中心系统有什么优势
在随着企业的管理水平也在不断提高。企业经营管理中所涉及到的各种复杂问题都有逐渐凸显出来。传统的呼叫中心已无法满足企业服务需求和客户满意度变化的要求。因此通过呼叫中心系统将企业业务流程和数据整合起来进行管理和运营已经成为目前企业管理领域中较为流行和成熟之选。…...
如何在linux操作系统下安装nvm
本文主要介绍如何在linux操作系统下安装nvm,如果想知道nvm如何在windows操作系统下使用,请参考文章如何通过nvm管理多个nodejs版本_nvm 查看所有node版本-CSDN博客。 1、nvm下载 nvm全称Node Version Manager,即Node版本管理器。访问官网地址…...
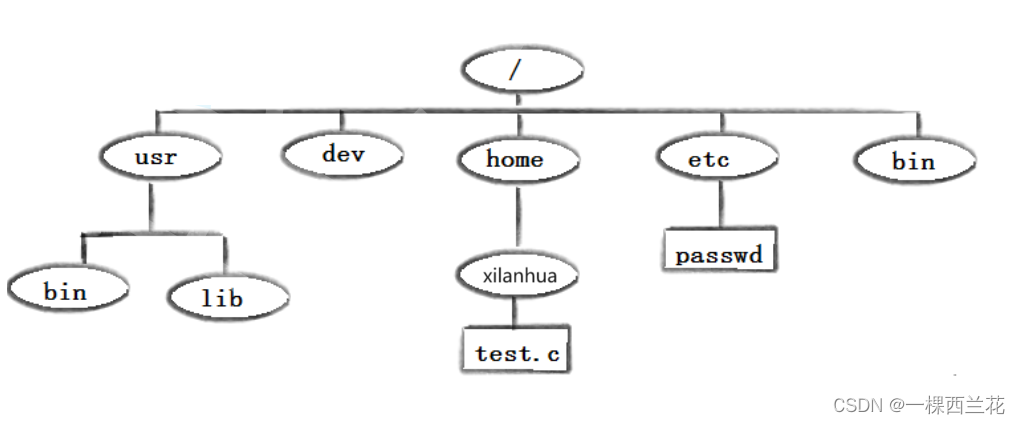
Linux 入门:基本指令
本篇文章来介绍我们在初学Linux时可以会碰倒的一些基本指令,让我们对这些指令有一个基本的了解。 目录 01. ls 指令 02. pwd 命令 03. cd 指令 04. touch 指令 05. mkdir 指令(重要) 06. rmdir指令 && rm 指令(重…...

IP转地理位置:探讨技术与应用
IP地址是互联网上设备的唯一标识符,而将IP地址转换为地理位置信息是网络管理、安全监控和市场定位等领域中的一项重要任务。本文将深入探讨IP转地理位置的技术原理和各种应用场景。 IP地址与地理位置 IP地址(Internet Protocol Address)是一…...

关于埋点上报
一、埋点上报结构包含哪些? 埋点上报结构一般包含以下信息: 事件名称:标识上报的是哪个事件,例如“注册成功”或“点击按钮”等。事件发生时间:记录事件发生的时间戳。用户ID:标识事件所属的用户。设备信息…...

最新博客园图片上传接口,模拟实现图片上传
简单看了一下博客园的图片上传接口,可以拿来做图床工具,仅供参考学习,请勿滥用。 1、实例代码 #!/usr/bin/python # -*- coding: UTF-8 -*- """ author: Roc-xb """import requestsurl "https://uplo…...

ROS2 从头开始:第 08/8回 - 使用 ROS2 生命周期节点简化机器人软件组件管理
一、说明 欢迎来到我在 ROS2 上的系列的第八部分。对于那些可能不熟悉该系列的人,我已经涵盖了一系列主题,包括 ROS2 简介、如何创建发布者和订阅者、自定义消息和服务创建、...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...