【高阶数据结构】哈希的应用 {位图;std::bitset;位图的应用;布隆过滤器;布隆过滤器的应用}
一、位图
1.1 位图概念
-
面试题
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。【腾讯】 -
遍历查找:内存中无法存放40亿个整数(约占内存15-16G);时间复杂度O(N);
-
先排序O(NlogN),再利用二分查找O(logN):数据太大,只能存放在磁盘文件中,数据读取速度慢。
-
位图
数据是否在给定的集合中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。利用位图解决该问题,无符号整数的取值范围是0~2^32,一个位代表一个整数,只需要2^32bit = 512MB内存空间即可。

-
位图概念
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。数据的键值通过直接定址法与位图中的位建立联系。
提示:位图在STL中的实现为bitset,在头文件<bitse>中声明
1.2 位图的实现
关于位运算的相关知识请阅读:
【C语言进阶】位运算 {位运算符;位运算符的优先级;位运算的应用 :关闭位,判断位,打开位,转置位;位域}
#include <vector>
#include <math.h>
using namespace std; namespace zty{ template <size_t N> class bitset{ vector<char> _bt; size_t _count; public: bitset() :_bt(ceil((double)N/8)), //ceil向上取整 _count(0) {} //打开位 void set(size_t x){ if(x>N) return; size_t i = x/8; //计算在第几个char类型 size_t j = x%8; //计算在char类型的第几位 _bt[i] |= (1<<j); ++_count; } //关闭位void reset(size_t x){if(x>N) return;size_t i = x/8;size_t j = x%8;_bt[i] &= ~(1<<j);--_count;}//判断位 bool test(size_t x){if(x>N) return false;size_t i = x/8;size_t j = x%8;return _bt[i] & (1<<j);}//返回bitset中被置为1的比特位数size_t count(){return _count;}//返回bitset中的比特位总数size_t size(){return N;}};
}
1.3 位图应用
- 快速查找某个数据是否在一个集合中
- 排序 + 去重
- 求两个集合的交集、并集等
- 操作系统中磁盘块标记
相关面试题
- 给定100亿个整数,设计算法找到只出现一次的整数?
思路:
- 每个整数有3种状态:出现0次;出现1次;出现2次及以上
- 需要两个位图解决
template <size_t N>class twobitset1{bitset<N> bs1;bitset<N> bs2;public:void set(size_t x){if(!bs1.test(x) && !bs2.test(x)) //出现0次(00)-->出现1次(01){bs2.set(x);}else if(!bs1.test(x) && bs2.test(x)) //出现1次(01)-->出现2次(10){bs1.set(x);bs2.reset(x);}}void print_once_num(){for(size_t i = 0; i<N; ++i){//找到只出现一次的整数(01)if(!bs1.test(i) && bs2.test(i)){cout << i << " ";}}cout << endl;}};void test1(){int arr[] = {6,99,1,1,2,4,3,5,6,7,1,3,2,4,7,9,8,5,4,3,21,8,9,4,2,3,1,4,3,57};zty::twobitset1<100> tbs;for(int e : arr){tbs.set(e);}tbs.print_once_num();
}
-
给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
思路:每个文件对应一个位图,两位图的对应位都为1就是交集。
template <size_t N>class twobitset2{bitset<N> bs1; //文件1对应的位图bitset<N> bs2; //文件2对应的位图public:void setbs1(size_t x){bs1.set(x);} void setbs2(size_t x){bs2.set(x);} void print_intersection_set(){for(size_t i = 0; i<N; ++i){//找出两个文件中数据的交集(11)if(bs1.test(i) && bs2.test(i)){cout << i << " ";}}cout << endl;}};void test2(){int file1[] = {6,99,1,1,2,4,3,5,6,7,1,3,2,4,7,9,8,5,4,3,21,8,9,4,2,3,1,4,3,57};int file2[] = {5,3,1,5,12,23,45,6,78,9,12,13,15,57,3,4,9};zty::twobitset2<100> tbs;for(int e : file1){tbs.setbs1(e);}for(int e : file2){tbs.setbs2(e);}tbs.print_intersection_set(); } -
位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
思路:
- 每个整数有4种状态:出现0次;出现1次;出现2次;出现3次及以上
- 需要两个位图解决
template <size_t N>class twobitset3{bitset<N> bs1;bitset<N> bs2;public:void set(size_t x){if(!bs1.test(x) && !bs2.test(x)) //出现0次(00)-->出现1次(01){bs2.set(x);}else if(!bs1.test(x) && bs2.test(x)) //出现1次(01)-->出现2次(10){bs1.set(x);bs2.reset(x);}else if(bs1.test(x) && !bs2.test(x)) //出现2次(10)-->出现3次(11){bs2.set(x);}}void print_atmost_twice(){//找到出现次数不超过2次的所有整数for(size_t i = 0; i<N; ++i){if(!bs1.test(i) && bs2.test(i)) //出现1次(01){cout << i << " ";}else if(bs1.test(i) && !bs2.test(i)) //出现2次(10){cout << i << " ";}}cout << endl;}};void test3(){int arr[] = {1,1,1,2,2,2,3,4,4,4,4,4,5,5,6};zty::twobitset3<100> tbs;for(int e : arr){tbs.set(e);}tbs.print_atmost_twice();
}
二、布隆过滤器
2.1 布隆过滤器概念
-
位图一般只能解决整形数据在或不在的问题,如果数据是字符串或者其他类型,可以先将其转换为无符号整型再插入位图。但这样的处理方式存在哈希冲突的概率比较大。
-
哈希表需要将数据全部加载到内存中还要开辟额外的指针(链表指针)和数组空间(负载因子),面对海量数据会占用大量的内存,甚至可能出现内存空间不够用的情况。
-
于是诞生了新的容器——布隆过滤器。布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函数,将一个数据映射到位图结构中的多个位上,以此来降低哈希冲突的概率。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
-
布隆过滤器虽然可以降低哈希冲突的概率但不可完全避免。因此布隆过滤器可能发生误判:**不存在一定是准确的,但存在则可能发生误判。**误判率可以通过增加哈希函数(映射位数)来进一步降低。理论而言,一个值映射的位越多,误判率越低,但同时空间消耗也就越多
提示:STL没有实现布隆过滤器,如有需要请自行实现。
2.2 布隆过滤器的结构
布隆过滤器的结构实际就是一个位图:

2.2.1 插入
如果我们要映射一个值到布隆过滤器中,我们需要使用多个不同的哈希函数生成**多个哈希值,**并对每个生成的哈希值指向的 bit 位置 1,例如针对值 “baidu” 和三个不同的哈希函数分别生成了哈希值 1、4、7,则上图转变为:

2.2.2 查找
-
布隆过滤器的思想是将一个元素用多个哈希函数映射到一个位图中,因此被映射到的位置的比特位一定为1。所以可以按照以下方式进行查找:分别计算每个哈希值对应的比特位置存储的是否为零,只要有一个为零,代表该元素一定不在哈希表中,否则可能在哈希表中。
-
比如:在布隆过滤器中查找:“tencent”

假设3个哈希函数计算的哈希值为:3、4、8,虽然"baidu"和"tencent"两者通过Hash2计算的哈希值(4)相同,造成哈希冲突。但Hash1和Hash3的计算结果不同,只要三个哈希值中有一个位为0就能确定该字符串不存在。
-
再比如:在布隆过滤器中查找:“alibaba”

假设3个哈希函数计算的哈希值为:1、4、7,刚好和"baidu"的比特位全部重叠。此时布隆过滤器返回该元素存在,但实际该元素是不存在的,发生误判。
- 综上所述:布隆过滤器如果说某个元素不存在时,该元素一定不存在,如果该元素存在时,该元素可能存在,因为有些哈希函数存在一定的误判。
2.2.3 删除
布隆过滤器不能直接支持删除工作,原因有二:
-
在删除一个元素时,如果直接将该元素所对应的二进制比特位置0,而该元素恰好与其他元素有重叠的位,就会导致这些重叠元素也被删除。
-
不能确定待删除元素本身是存在于布隆过滤器的,可能会导致误删。
2.3 如何选择哈希函数个数和布隆过滤器长度
很显然,过小的布隆过滤器很快所有的 bit 位均为 1,那么查询任何值都会返回“可能存在”,起不到过滤的目的了。布隆过滤器的长度会直接影响误报率,布隆过滤器越长其误报率越小。
另外,哈希函数的个数也需要权衡,个数越多则布隆过滤器 bit 位置位 1 的速度越快,且布隆过滤器的效率越低;但是如果太少的话,那我们的误报率会变高。

如何选择适合业务的 k 和 m 值呢,这里直接贴一个公式:

例如:当k为3时,m≈4.2n,我们向上取整为5。即布隆过滤器的长度是插入元素个数的5倍。
2.4 布隆过滤器的实现
//三种字符串哈希算法struct BKDRHash{size_t operator()(const string& s){// BKDRsize_t value = 0;for (auto ch : s){value += ch;value *= 31;}return value;}};struct APHash{size_t operator()(const string& s){size_t hash = 0;for (size_t i = 0; i < s.size(); i++){if ((i & 1) == 0){hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));}}return hash;}};struct DJBHash{size_t operator()(const string& s){size_t hash = 5381;for (auto ch : s){hash += (hash << 5) + ch;}return hash;}};//布隆过滤器//N是要插入的元素个数//布隆过滤器默认处理字符串template <size_t N, class K = string,class Hash1 = BKDRHash,class Hash2 = APHash,class Hash3 = DJBHash>class BloomFilter{std::bitset<N*5> _bs; //当哈希函数的个数为3时,布隆过滤器的长度是插入元素个数的5倍public:void set(const K& key){//将三个哈希函数计算得到映射位置置1size_t hashi1 = Hash1()(key) % _bs.size(); //_bs.size()-->N*5_bs.set(hashi1);size_t hashi2 = Hash2()(key) % _bs.size();_bs.set(hashi2);size_t hashi3 = Hash3()(key) % _bs.size();_bs.set(hashi3);}bool test(const K& key){//只要三个哈希函数计算得到映射位置中有一个位为0就返回falsesize_t hashi1 = Hash1()(key) % _bs.size();if(!_bs.test(hashi1)) return false; //准确的size_t hashi2 = Hash2()(key) % _bs.size();if(!_bs.test(hashi2)) return false; //准确的size_t hashi3 = Hash3()(key) % _bs.size();if(!_bs.test(hashi3)) return false; //准确的return true; //可能存在误判}};
测试代码:
//简单测试
void TestBloomFilter1()
{zty::BloomFilter<11> bf;string arr1[] = { "苹果", "西瓜", "阿里", "美团", "苹果", "字节", "西瓜", "苹果", "香蕉", "苹果", "腾讯" };for (auto& str : arr1){bf.set(str);}for (auto& str : arr1){cout << bf.test(str) << endl;}cout << endl << endl;string arr2[] = { "苹果111", "西瓜", "阿里2222", "美团", "苹果dadcaddxadx", "字节", "西瓜sSSSX", "苹果", "香蕉", "苹果$", "腾讯" };for (auto& str : arr2){cout <<str<<":"<<bf.test(str) << endl;}
}//误判率测试
void TestBloomFilter2()
{srand(time(0));const size_t N = 100000;zty::BloomFilter<N> bf;cout << "sizeof BloomFilter: " << sizeof(bf) << endl; std::vector<std::string> v1;std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";for (size_t i = 0; i < N; ++i){v1.push_back(url + std::to_string(1234 + i));}for (auto& str : v1){bf.set(str);}//测试相似字符串误判率:std::vector<std::string> v2;for (size_t i = 0; i < N; ++i){std::string url = "http://www.cnblogs.com/-clq/archive/2021/05/31/2528153.html";url += std::to_string(rand() + i);v2.push_back(url);}size_t n2 = 0;for (auto& str : v2){if (bf.test(str)){++n2;}}cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;//测试不相似字符串误判率:std::vector<std::string> v3;for (size_t i = 0; i < N; ++i){string url = "zhihu.com";url += std::to_string(rand()+i);v3.push_back(url);}size_t n3 = 0;for (auto& str : v3){if (bf.test(str)){++n3;}}cout << "不相似字符串误判率:" << (double)n3 / (double)N << endl;
}
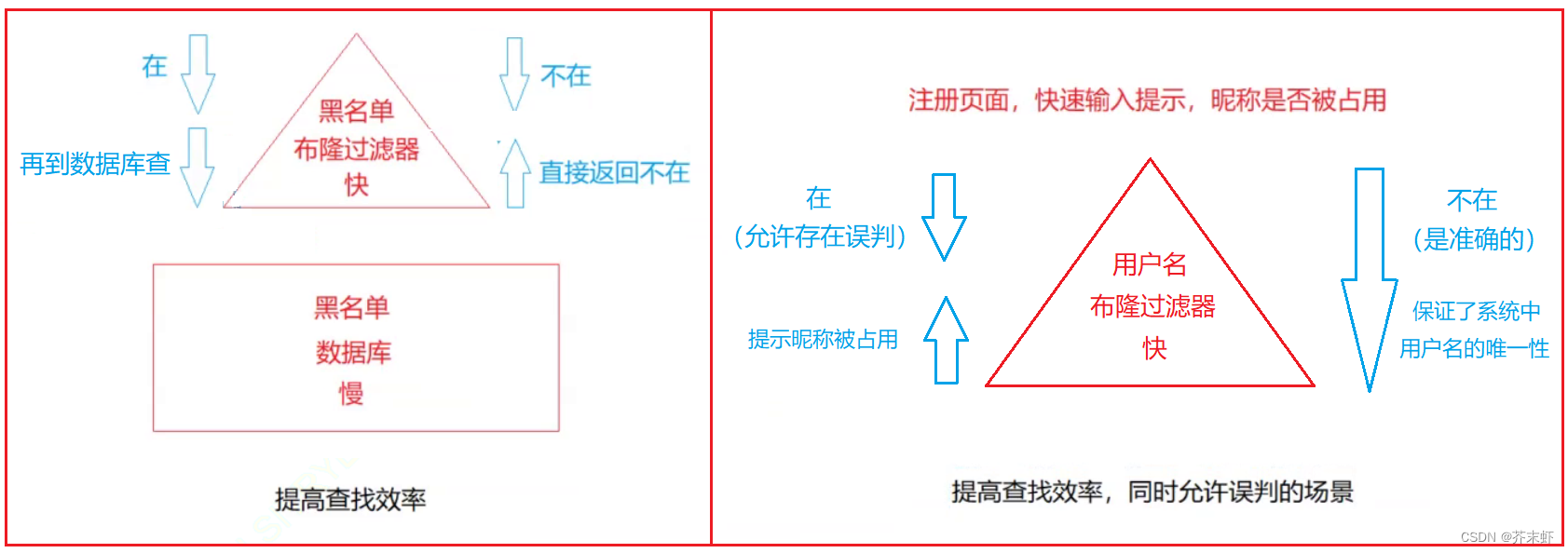
2.5 布隆过滤器的应用
提高查找效率:利用布隆过滤器减少磁盘 IO 或者网络请求,因为一旦一个值必定不存在的话,我们可以不用进行后续昂贵的查询请求。
海量数据处理:
给两个文件,分别有100亿个query(字符串),我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法
-
近似算法:将其中一个文件中的query插入到布隆过滤器中,再在布隆过滤器中遍历查找另一个文件的query。如果找到就是交集。近似算法的问题有:1.可能存在误判 2.没有进行去重
-
精确算法:哈希切分

哈希切分:
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址?如何找到top K的IP?

拓展:一致性哈希
2.6 布隆过滤器的优缺点
-
优点
-
插入和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
-
哈希函数相互之间没有关系,方便硬件并行运算
-
布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
-
在能够承受一定的误判时,布隆过滤器相比其他数据结构有很大的空间优势
-
数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
-
使用同一组散列函数的布隆过滤器可以进行交、并、差运算
-
-
缺点
- 有误判率,即存在假阳性(False Position),即不能准确判断元素在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)
- 不能获取元素本身
- 一般情况下不能从布隆过滤器中删除元素
相关文章:

【高阶数据结构】哈希的应用 {位图;std::bitset;位图的应用;布隆过滤器;布隆过滤器的应用}
一、位图 1.1 位图概念 面试题 给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。【腾讯】 遍历查找:内存中无法存放40亿个整数(约占内存15-16G);时间复杂…...
金融生产存储亚健康治理:升级亚健康 3.0 ,应对万盘规模的挑战
随着集群规模的不断扩大,硬盘数量指数级上升,信创 CPU 和操作系统、硬盘多年老化、物理搬迁等多种复杂因素叠加,为企业的存储亚健康管理增加了新的挑战。 在亚健康 2.0 的基础上,星辰天合在 XSKY SDS V6.2 实现了亚健康 3.0&#…...
C语言自定义类型讲解:结构体,枚举,联合(2)
🐵本篇文章将会对位段、枚举和联合的相关知识进行讲解 1. 位段📚 1.1 什么是位段 位段的声明和结构体类似,但是有两点不同: 1.位段的成员必须是int,unsigned int,signed int (C99之后也可以是其他成员&am…...

AI编程助手 Amazon CodeWhisperer 全面解析与实践
目录 引言Amazon CodeWhisperer简介智能编程助手智能代码建议代码自动补全 提升代码质量代码质量提升安全性检测 支持多平台多语言 用户体验和系统兼容性用户体验文档和学习资源个性化体验系统兼容性 功能全面性和代码质量功能全面性代码生成质量和代码安全性 CodeWhisperer的代…...

利用EXCEL进行XXE攻击
利用EXCEL进行XXE攻击 原因 原因 Microsoft Office从2007版本引入了新的开放的XML文件格式,新的XML文件格式基于压缩的ZIP文件格式规范,由许多部分组成。 我们可以将其解压缩到特定的文件夹中来查看其包含的文件夹和文件,可以发现其中多数是…...

芯片验证就是一次旅行
如果你国庆希望去一个你不曾去过的城市旅行,比如“中国苏州”。对游客来说,它是个蛮大的城市,有许多景点可以游玩,还有许多事情可以做。但实际上,即使最豪也最清闲的游客也很难看苏州的所有方方面面。同样的道理也适用…...
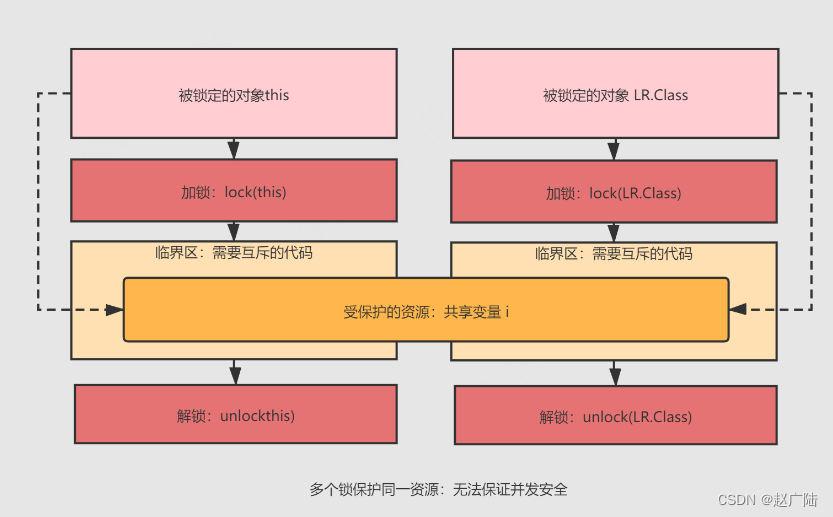
Java深入理解线程的三大特性
目录 1 CPU缓存导致可见性问题2 线程切换导致原子性问题3 性能优化导致有序性问题4 JMM(Java Memory Model)5 volatile6 synchronized 1 CPU缓存导致可见性问题 线程的三大特性: 可见性:Visibility有序性:Ordering原子性:Atomic…...
)
2025快手校招面试真题汇总及其解答(二)
6. hashmap数据结构 HashMap 是一种散列表,它是一种根据键值对来存储数据的数据结构。HashMap 的特点是插入、查找和删除操作的时间复杂度都是 O(1),因此它是一种非常高效的数据结构。 HashMap 的工作原理是将键值对存储在一个数组中,每个键值对都由一个哈希函数来映射到数…...

PHP生成带中文的图片
imagettftext() 函数是 PHP 中的一个内置函数,用于使用 TrueType 字体将文本写入图像。 句法: 数组imagettftext(资源$image,float $size,float $angle, int $x,int $y,…...
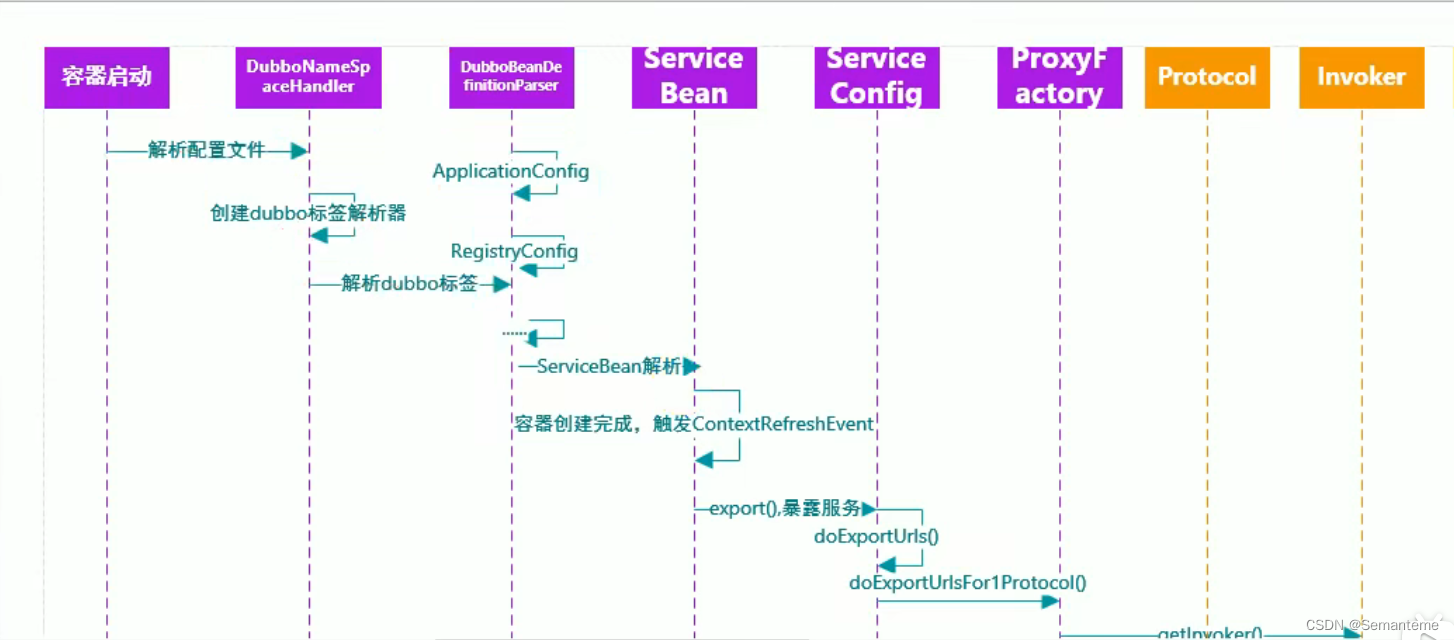
java框架-Dubbo
Dubbo整合Springboot BIO NIO Netty Dubbo 原理 在这里插入图片描述...
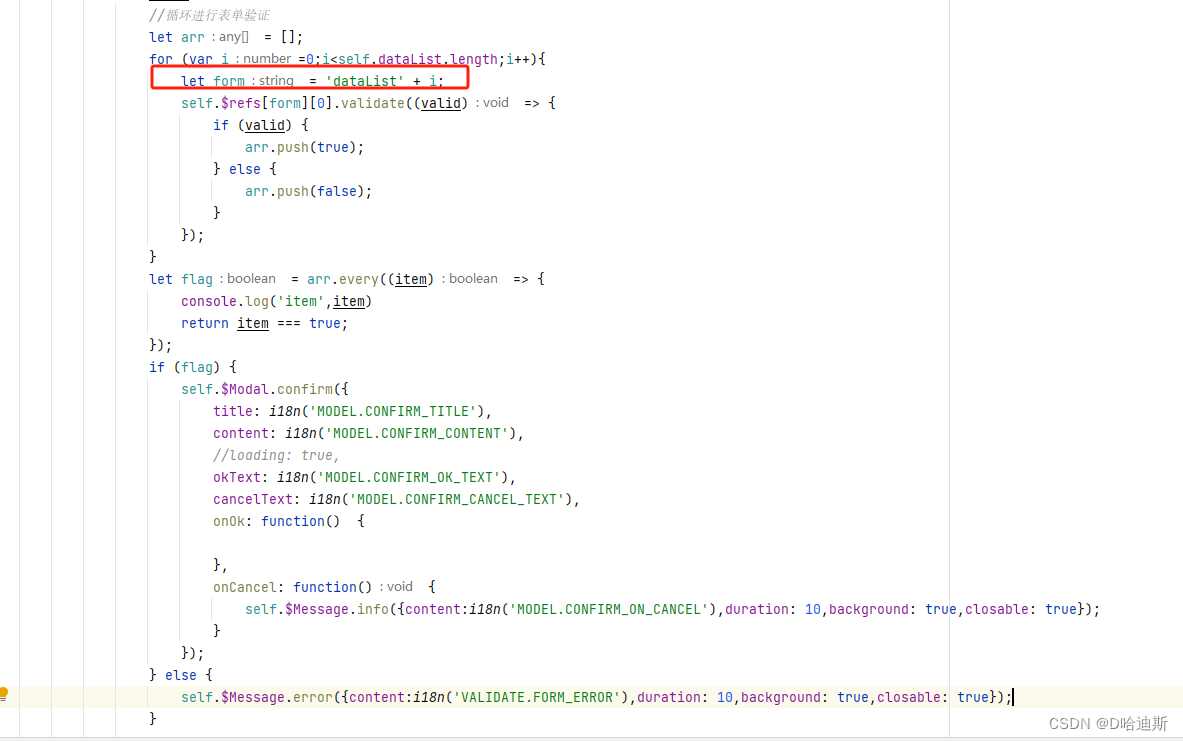
Vue+iview 组件中通过v-for循环动态生成form表单进行表单校验
在做项目时,需要根据需要动态添加或新增表单,同时还需要对表单做校验。详情如下图: 刚开始做表单验证的时候,对于这个动态的表单验证有点难搞,试了好几种方法都没有搞定。最后按照下面这种方法实现了,以此…...
sns.load_dataset(“iris“)报错原因探究+解决办法
问题描述 import seaborn as sns # 读取数据 iris sns.load_dataset("iris")在代码中使用了seaborn ,并加载iris数据,结果产生了报错信息如下所示 问题分析 原因很简单,我们使用了sns.load_dataset("iris")来加载数据…...

python回文素数
这能有1和本身整除的整数叫素数;如一个素数从左向右和从右向左是相同的数,则该素数为回文素数。编程求出2-1000内的所有回文素数。 源代码: def sushu(n): for i in range(2,n//21): if n%i 0: return False r…...
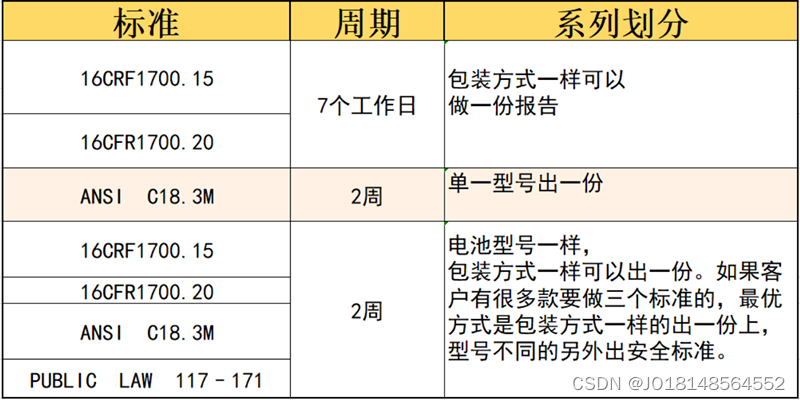
纽扣电池16CRF1700.15,16CFR1700.20,ANSI C18.3M如何申请?
随着科技的发展,纽扣电池被广泛应用于小型电子产品,如计算器、电子手表、玩具、医疗设备等。由于其体积小,易于拆卸,也造成了儿童误吞的潜在风险。因此,对于纽扣电池的认证和包装,各国均有相应的规定。 在美…...

10.12广州见 | 第十六届智慧城市大会报名通道全面开启
第十六届中国智慧城市大会 将于10月12日至13日 在广州举办 智慧城市是数字中国、智慧社会的核心载体,是数字时代城市发展的高级形态。由中国服务贸易协会、中国测绘学会、中国遥感委员会主办的第十六届中国智慧城市大会,将以“数实融合开放创新智引未…...

2023-油猴(Tampermonkey)脚本推荐
2023-油猴(Tampermonkey)脚本推荐 知乎增强 链接 https://github.com/XIU2/UserScript https://greasyfork.org/zh-CN/scripts/419081 介绍 移除登录弹窗、屏蔽首页视频、默认收起回答、快捷收起回答/评论(左键两侧)、快捷回…...
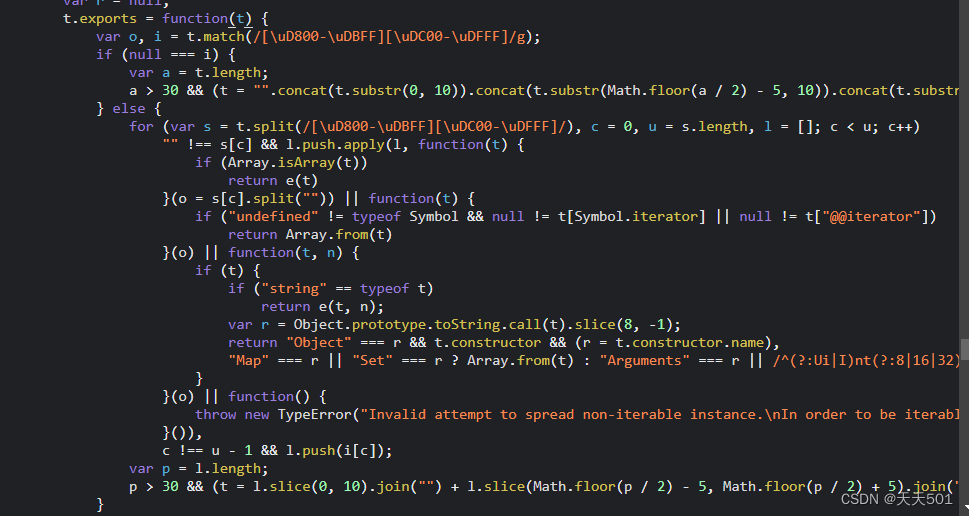
某度sign参数逆向
文章目录 前文分析完整代码结尾 前文 本文章中所有内容仅供学习交流,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关,若有侵权,请联系我立即删除! 分析 经过我们几次抓包,测试…...

【选型】JAVA生成PPT及选型
可以使用的框架(类库):POI,OpenOffice/LibreOffice,Aspose.Slides,Java开源报表工具(JasperReports,BIRT等)。 具体如下: 方案优点缺点Apache POI- 开源免费- 可完全控制PPT生成- …...

LPA*算法图文详解
之前我们看过了A* 算法,知道了A* 算法的基本原理,但是A* 算法的缺陷也很明显:它是离线的路径规划算法,只能一次规划出路径,但是后面路径被改变的话就无法生效了。针对这个问题,人们研究出了D* 算法。D* 算法…...
】)
【Unity的HDRP渲染管线下实现好用的GUI模糊和外描边流光效果_Blur_OutLine_案例分享(内附源码)】
实现好用的模糊效果_Blur HDRP渲染管线下搭建场景创建RenderTextureRenderTexture 与相机的配置:UI层 Canvas的不同Render Mode:Canvas 在Screen Space - Overlay 模式下:UI旋转Y轴,没有透视。切换到Screen Space - Camera 模式下:UI层跑到物体后面去了,将Plane Distance…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
