LPA*算法图文详解
之前我们看过了A* 算法,知道了A* 算法的基本原理,但是A* 算法的缺陷也很明显:它是离线的路径规划算法,只能一次规划出路径,但是后面路径被改变的话就无法生效了。针对这个问题,人们研究出了D* 算法。D* 算法相对于A* 也好还是Dijkstra算法也好它最大的优点就是再于它在运动过程中是实时的:在原先规划的路径上如果出现障碍物的话,会对当前路径进行新的规划,通过较短的迭代即可找到新的路径。但是它比较大的问题在于它只能处理空白路径上出现障碍物的情况,而不能处理本来是障碍物但是变成空白区域的情况。而针对这种情况,LPA* 算法诞生啦!
LPA* 算法基本原理:
LPA* 保持每个单元的起始距离的两个估计,即g值和rhs值。g值直接对应于A*搜索的g值。rhs值是基于g值的一步前瞻值。rhs值是始终满足以下关系(基于g值):

起始单元格的rhs值为零。任何其他位置的rhs值是邻居的g值和从周围格子移动到目标格子的成本的最小值。因此,在初始状态下每个栅格的g值等于其rhs值。我们称这种格子为局部一致的。这个概念很重要,因为所有g值都等于相应的起始距离,如果所有单元都是局部一致的。
当地图中障碍物发生变化的时候,该格子的rhs值会发生改变。此时格子的g值跟rhs值会变的不一致。对于g值跟rhs值不一致的栅格,称为局部不一致栅格。这里同样分为两种情况:
1、原来是障碍物的栅格移除了障碍物,对于这种情况,我们称之为局部过一致,即:
g ( s ) > r h s ( s ) g(s) > rhs(s) g(s)>rhs(s)
2、原来空白的栅格添加了新的障碍物,对于这种情况,我们称之为局部欠一致,即:
g ( s ) < r h s ( s ) g(s) < rhs(s) g(s)<rhs(s)
对于这两点,还是比较好理解的。对于原来是障碍物的点,它的rhs值以及g值本来都是无穷大,在将障碍物移除后,会更新rhs值,则根据上面的公式我们可以知道该值一定是一个确定的值(除非它周围所有点的g值都是无穷)。而同样的,本来一个空白的格子其g值应该等与rhs值,但是当其变为障碍物时,它的rhs值也会变成无穷,也就满足了局部欠一致的条件。
对于这两个情况,算法会分为两种不同的处理方式:

对于局部过一致的点位,会将其g值更新为rhs值,并同时更新其周围点位信息。对于局部欠一致的点位,会将其g值更新为无穷大,然后更新其周围点的信息。对于这里的UpdateVertex函数,原论文是这么定义的:

简单的来说,算法对于每个栅格的更新主要分为三步:
1、更新这个格子的rhs值,它的值为其周围所有栅格中,其g值加上这个栅格到目标栅格的h值之和的最小值。
2、如果这个栅格属于集合U,则将其移除U集合,因为每次需要更新的点位都是从集合U中选取的,对于遍历过的点位自然要先移除。
3、如果这个点位的g值跟rhs值不一致,则重新将其插入集合U。注意插入后的点的U的值跟之前的值应该是不一样的。这里关于U的值的计算遵循下述公式:

可以看到U其实是个两个数的集合,第一位数带了一步预测值,第二位数为其g值与rhs值中较小的那一个。
简单的来说,LPA* 的基本思想就是,首先利用A* 算法找到一条路径,同时维护每个栅格的两个值:g值与rhs值。然后在运动过程中,如果地图的障碍物发生变化,则更新其rhs值。此时g值与rhs值会不一致,这种栅格成为局部不一致栅格。然后算法通过ComputeShortestPath函数对这些局部不一致栅格进行处理,使其变得局部一致,在这个过程中也就找到了一条新的路径。
整个算法的总体原理流程图如下:

例子
讲了一堆,云里雾里,还是通过一个简单的例子来看一下这个问题:
 假设我们有如上场景,左下角浅绿色为起点,蓝色格子为终点,红色为障碍物,初始时,采用A* 算法我们规划出一条路径如下:
假设我们有如上场景,左下角浅绿色为起点,蓝色格子为终点,红色为障碍物,初始时,采用A* 算法我们规划出一条路径如下:
 同时我们得到每个栅格的g值与rhs值如下:
同时我们得到每个栅格的g值与rhs值如下:

其中左上角为g值右上角为rsh值。注意这里有几个点的g值为inf但是rsh值是确定值,这里是因为在更新某个点的时候会更新其周围点的rsh值,但是g值则需要更新这个点的时候才会更新。而A* 可以说是带有方向性的,不是所有点都会被遍历,因此会出现这个问题。但是不影响算法实际的使用。
局部过一致处理流程:
假设我们将(2,2)处的障碍物移除。首先算法会更新该点的rhs值。其值更新遵循文章最上面的公式。因此其rhs值会变为1.41:

对于上面被修改过的点,会被放入集合U作为不一致点进行处理。然后算法会进入ComputeShortestPath函数,更新这些不一致点的g值与rhs值。更新时取出点的逻辑为先取处集合U中(min(g(s), rhs(s)) + h(s))值最小的点。因此首先被取处的是(2,2),该点满足局部过一致条件,因此更新其g值等与rhs值。然后再更新其周围所有相邻点的值:
 在这个过程中有两个点被修改了,首先修改的是(2,2)点的g值,其被修改为与rhs值一致。此时该点位回归为局部一致点位,会将其从U中剔除,同时由于之前的点位(3,2)的rhs值被修改为2.41小于其g值,所以该点变为局部不一致点位,加入集合U。
在这个过程中有两个点被修改了,首先修改的是(2,2)点的g值,其被修改为与rhs值一致。此时该点位回归为局部一致点位,会将其从U中剔除,同时由于之前的点位(3,2)的rhs值被修改为2.41小于其g值,所以该点变为局部不一致点位,加入集合U。
然后算法再次从U中取处点位(3,2),执行ComputeShortestPath函数:
 这个过程点位(3,2)从集合U中删除,并将点位(3,3)加入集合。然后算法再次从U中取处点位(3,3),执行ComputeShortestPath函数:
这个过程点位(3,2)从集合U中删除,并将点位(3,3)加入集合。然后算法再次从U中取处点位(3,3),执行ComputeShortestPath函数:

这个过程点位(3,3)从集合U中删除,并将点位(3,4)加入集合。然后算法再次从U中取处点位(3,4),执行ComputeShortestPath函数:
 这个过程点位(3,4)从集合U中删除,并将点位(3,5)加入集合。然后算法再次从U中取处点位(3,5),执行ComputeShortestPath函数:
这个过程点位(3,4)从集合U中删除,并将点位(3,5)加入集合。然后算法再次从U中取处点位(3,5),执行ComputeShortestPath函数:
 这个过程点位(3,5)从集合U中删除,并将点位(3,6)、点位(4,5)、点位(4,6)加入集合。然后算法再次从U中取处点位(4,5),执行ComputeShortestPath函数:
这个过程点位(3,5)从集合U中删除,并将点位(3,6)、点位(4,5)、点位(4,6)加入集合。然后算法再次从U中取处点位(4,5),执行ComputeShortestPath函数:

这个过程点位(4,5)从集合U中删除,并将点位(5,5)、点位(5,6)加入集合。然后算法再次从U中取处点位(4,6),执行ComputeShortestPath函数:
 这个过程点位(4,6)从集合U中删除,但是周围点的rhs值都被更新过了,所以这一步没有新的点位加入集合。然后算法再次从U中取处点位(5,5),执行ComputeShortestPath函数:
这个过程点位(4,6)从集合U中删除,但是周围点的rhs值都被更新过了,所以这一步没有新的点位加入集合。然后算法再次从U中取处点位(5,5),执行ComputeShortestPath函数:

将点位(5,5)从集合U中删除,将点位(6,6)加入集合。算法再次从U中取处点位(5,6),执行ComputeShortestPath函数:
 将点位(5,6)从集合U中删除,算法再次从U中取处点位(6,6),执行ComputeShortestPath函数:
将点位(5,6)从集合U中删除,算法再次从U中取处点位(6,6),执行ComputeShortestPath函数:
 此时这些点都再次恢复了局部一致性,注意到其实在这个过程中还是存在局部不一致点位的,例如(3,6)一直没有更新。但是此时ComputeShortestPath函数已经不满足了,所以算法跳出了。该点也就不需要再次更新了。
此时这些点都再次恢复了局部一致性,注意到其实在这个过程中还是存在局部不一致点位的,例如(3,6)一直没有更新。但是此时ComputeShortestPath函数已经不满足了,所以算法跳出了。该点也就不需要再次更新了。
关于这里的判断,论文中是这么定义的:

所以对于点(3,6)而言,它的值应该为[9.41,6.41]。9.41为rhs(s)+h(s)的值。而终点的值为8.82小于9.41,所以(3,6)这个点怎么优化都不可能比现在的路径更短,自然不需要再更新了。
最后,我们可以得到更新后的路径为:

局部欠一致处理流程:
看完局部过一致流程,接下来我们再看一下局部欠一致处理流程。修改初始地图,假设初始时(2,2)点位为空白,得到地图路径为:

然后我们将(2,2)添加为障碍物,此时该点的rhs值为inf,然后将点位添加到集合U中,执行ComputeShortestPath函数:
 此时点(3,2)的rhs值被修改为3,该点变为局部不一致点位,加入集合U,同时从集合U中剔除点位(2,2),继续循环:
此时点(3,2)的rhs值被修改为3,该点变为局部不一致点位,加入集合U,同时从集合U中剔除点位(2,2),继续循环:
 根据ComputeShortestPath函数算法首先更新点(3,2)的g值,由于这个点是局部欠一致点位,所以其g值应该直接更新为inf,同时更新点(3,2)周围点的rhs值:
根据ComputeShortestPath函数算法首先更新点(3,2)的g值,由于这个点是局部欠一致点位,所以其g值应该直接更新为inf,同时更新点(3,2)周围点的rhs值:
 然后更新点(3,3)的g值,同时更新点(3,3)周围点的rhs值:
然后更新点(3,3)的g值,同时更新点(3,3)周围点的rhs值:
 然后更新点(3,2)的g值,同时更新点(4,3)周围点的rhs值:此时该点为过一致点,按照前面过一致点进行处理:
然后更新点(3,2)的g值,同时更新点(4,3)周围点的rhs值:此时该点为过一致点,按照前面过一致点进行处理:
 这样子,点(2,2)与点(3,2)都恢复了局部一致性,然后更新点(3,4):
这样子,点(2,2)与点(3,2)都恢复了局部一致性,然后更新点(3,4):
 然后处理点(3,3):
然后处理点(3,3):

然后处理点(3,5):

然后处理点(3,4):
 然后处理点(4,5):
然后处理点(4,5):
 然后处理点(4,6):
然后处理点(4,6):
 然后处理点(5,5):
然后处理点(5,5):
 然后处理点(5,6):
然后处理点(5,6):
 然后处理点(6,6):
然后处理点(6,6):

中间省略一部分迭代过程(1,5)》(5,1)》(5,2)》(3,5)》(5,3)》(4,5)》(5,4)》(6,2)》(6,3)》(4,6)》(6,4)》(5,5)》(5,6)》(6,5)》(6,6),得到最终结果为:

小结
总体来说LPA* 算法的思路就是使用两个列表维护每个栅格的值,当两个值不一致时,称该栅格为局部不一致,则根据ComputeShortestPath函数更新每个栅格的值,对于原来是障碍物后面消除的情况称为局部过一致点,处理起来会比较容易,对于原来是空白点位后面变成障碍物的称为局部欠一致点,处理情况会略微复杂一点,首先会将点变为局部过一致点,再按照局部过一致点的处理方式再处理一遍,最后达到点位的一致性,同时对于不一致点的遍历原则会类似于A* 算法的遍历方式,这样会提高点位的遍历效率。
代码实现:
import os
import sys
import math
import matplotlib.pyplot as pltclass LPAStar:def __init__(self, s_start, s_goal, heuristic_type,xI, xG):self.xI, self.xG = xI, xGself.x_range = 51 # size of backgroundself.y_range = 31self.motions = [(-1, 0), (-1, 1), (0, 1), (1, 1),(1, 0), (1, -1), (0, -1), (-1, -1)] # feasible input setself.obs = self.obs_map()self.s_start, self.s_goal = s_start, s_goalself.heuristic_type = heuristic_typeself.u_set = self.motionsself.obs = self.obsself.x = self.x_rangeself.y = self.y_rangeself.g, self.rhs, self.U = {}, {}, {}for i in range(self.x_range):for j in range(self.y_range):self.rhs[(i, j)] = float("inf")self.g[(i, j)] = float("inf")self.rhs[self.s_start] = 0self.U[self.s_start] = self.CalculateKey(self.s_start)self.visited = set()self.count = 0self.fig = plt.figure()def obs_map(self):"""Initialize obstacles' positions:return: map of obstacles"""x = 51y = 31obs = set()for i in range(x):obs.add((i, 0))for i in range(x):obs.add((i, y - 1))for i in range(y):obs.add((0, i))for i in range(y):obs.add((x - 1, i))for i in range(10, 21):obs.add((i, 15))for i in range(15):obs.add((20, i))for i in range(15, 30):obs.add((30, i))for i in range(16):obs.add((40, i))return obsdef update_obs(self, obs):self.obs = obsdef plot_grid(self, name):obs_x = [x[0] for x in self.obs]obs_y = [x[1] for x in self.obs]plt.plot(self.xI[0], self.xI[1], "bs")plt.plot(self.xG[0], self.xG[1], "gs")plt.plot(obs_x, obs_y, "sk")plt.title(name)plt.axis("equal")def plot_path(self, path, cl='r', flag=False):path_x = [path[i][0] for i in range(len(path))]path_y = [path[i][1] for i in range(len(path))]if not flag:plt.plot(path_x, path_y, linewidth='3', color='r')else:plt.plot(path_x, path_y, linewidth='3', color=cl)plt.plot(self.xI[0], self.xI[1], "bs")plt.plot(self.xG[0], self.xG[1], "gs")plt.pause(0.01)def run(self):self.plot_grid("Lifelong Planning A*")self.ComputeShortestPath()self.plot_path(self.extract_path())self.fig.canvas.mpl_connect('button_press_event', self.on_press)plt.show()def on_press(self, event):x, y = event.xdata, event.ydataif x < 0 or x > self.x - 1 or y < 0 or y > self.y - 1:print("Please choose right area!")else:x, y = int(x), int(y)print("Change position: s =", x, ",", "y =", y)self.visited = set()self.count += 1if (x, y) not in self.obs:self.obs.add((x, y))self.UpdateVertex((x, y))else:self.obs.remove((x, y))self.UpdateVertex((x, y))self.update_obs(self.obs)#for s_n in self.get_neighbor((x, y)):# self.UpdateVertex(s_n)self.ComputeShortestPath()plt.cla()self.plot_grid("Lifelong Planning A*")self.plot_visited(self.visited)self.plot_path(self.extract_path())self.fig.canvas.draw_idle()def ComputeShortestPath(self):while True:s, v = self.TopKey()if v >= self.CalculateKey(self.s_goal) and \self.rhs[self.s_goal] == self.g[self.s_goal]:breakself.U.pop(s)self.visited.add(s)if self.g[s] > self.rhs[s]:# Condition: over-consistent (eg: deleted obstacles)# So, rhs[s] decreased -- > rhs[s] < g[s]self.g[s] = self.rhs[s]else:# Condition: # under-consistent (eg: added obstacles)# So, rhs[s] increased --> rhs[s] > g[s]self.g[s] = float("inf")self.UpdateVertex(s)for s_n in self.get_neighbor(s):self.UpdateVertex(s_n)def UpdateVertex(self, s):"""update the status and the current cost to come of state s.:param s: state s"""if s != self.s_start:# Condition: cost of parent of s changed# Since we do not record the children of a state, we need to enumerate its neighborsself.rhs[s] = min(self.g[s_n] + self.cost(s_n, s)for s_n in self.get_neighbor(s))if s in self.U:self.U.pop(s)if self.g[s] != self.rhs[s]:# Condition: current cost to come is different to that of last time# state s should be added into OPEN set (set U)self.U[s] = self.CalculateKey(s)#print(self.U[s])def TopKey(self):""":return: return the min key and its value."""s = min(self.U, key=self.U.get)return s, self.U[s]def CalculateKey(self, s):return [min(self.g[s], self.rhs[s]) + self.h(s),min(self.g[s], self.rhs[s])]def get_neighbor(self, s):"""find neighbors of state s that not in obstacles.:param s: state:return: neighbors"""s_list = set()for u in self.u_set:s_next = tuple([s[i] + u[i] for i in range(2)])if s_next not in self.obs:s_list.add(s_next)return s_listdef h(self, s):"""Calculate heuristic.:param s: current node (state):return: heuristic function value"""heuristic_type = self.heuristic_type # heuristic typegoal = self.s_goal # goal nodeif heuristic_type == "manhattan":return abs(goal[0] - s[0]) + abs(goal[1] - s[1])else:return math.hypot(goal[0] - s[0], goal[1] - s[1])def cost(self, s_start, s_goal):"""Calculate Cost for this motion:param s_start: starting node:param s_goal: end node:return: Cost for this motion:note: Cost function could be more complicate!"""if self.is_collision(s_start, s_goal):return float("inf")return math.hypot(s_goal[0] - s_start[0], s_goal[1] - s_start[1])def is_collision(self, s_start, s_end):if s_start in self.obs or s_end in self.obs:return Trueif s_start[0] != s_end[0] and s_start[1] != s_end[1]:if s_end[0] - s_start[0] == s_start[1] - s_end[1]:s1 = (min(s_start[0], s_end[0]), min(s_start[1], s_end[1]))s2 = (max(s_start[0], s_end[0]), max(s_start[1], s_end[1]))else:s1 = (min(s_start[0], s_end[0]), max(s_start[1], s_end[1]))s2 = (max(s_start[0], s_end[0]), min(s_start[1], s_end[1]))if s1 in self.obs or s2 in self.obs:return Truereturn Falsedef extract_path(self):"""Extract the path based on the PARENT set.:return: The planning path"""path = [self.s_goal]s = self.s_goalfor k in range(100):g_list = {}for x in self.get_neighbor(s):if not self.is_collision(s, x):g_list[x] = self.g[x]s = min(g_list, key=g_list.get)path.append(s)if s == self.s_start:breakreturn list(reversed(path))def plot_path(self, path):px = [x[0] for x in path]py = [x[1] for x in path]plt.plot(px, py, linewidth=2)plt.plot(self.s_start[0], self.s_start[1], "bs")plt.plot(self.s_goal[0], self.s_goal[1], "gs")def plot_visited(self, visited):color = ['gainsboro', 'lightgray', 'silver', 'darkgray','bisque', 'navajowhite', 'moccasin', 'wheat','powderblue', 'skyblue', 'lightskyblue', 'cornflowerblue']if self.count >= len(color) - 1:self.count = 0for x in visited:plt.plot(x[0], x[1], marker='s', color=color[self.count])def main():x_start = (5, 5)x_goal = (45, 25)lpastar = LPAStar(x_start, x_goal, "Euclidean",x_start,x_goal)lpastar.run()if __name__ == '__main__':main()初始状态下规划结果为:

消除某个障碍物:

添加一个新的障碍物:

参考:
1、《终身规划A算法(LPA):Lifelong Planning A*》
2、《LPA* 路径搜索算法介绍及完整代码》
3、《路径规划算法》
相关文章:

LPA*算法图文详解
之前我们看过了A* 算法,知道了A* 算法的基本原理,但是A* 算法的缺陷也很明显:它是离线的路径规划算法,只能一次规划出路径,但是后面路径被改变的话就无法生效了。针对这个问题,人们研究出了D* 算法。D* 算法…...
】)
【Unity的HDRP渲染管线下实现好用的GUI模糊和外描边流光效果_Blur_OutLine_案例分享(内附源码)】
实现好用的模糊效果_Blur HDRP渲染管线下搭建场景创建RenderTextureRenderTexture 与相机的配置:UI层 Canvas的不同Render Mode:Canvas 在Screen Space - Overlay 模式下:UI旋转Y轴,没有透视。切换到Screen Space - Camera 模式下:UI层跑到物体后面去了,将Plane Distance…...
电脑D盘格式化会有什么影响?电脑D盘格式化了怎么恢复数据
当电脑出现问题时,往往会出现一些提示,例如提示格式化的问题,而最近有位小伙伴也遇到了相似的问题,即D盘一打开就显示格式化,由于不清楚D盘格式化会有什么影响,因此不小心进行了格式化操作,结果…...

【Spring】多环境切换
🎈博客主页:🌈我的主页🌈 🎈欢迎点赞 👍 收藏 🌟留言 📝 欢迎讨论!👏 🎈本文由 【泠青沼~】 原创,首发于 CSDN🚩…...

python经典百题之求10000之内的素数
题目:求10000之内的素数 程序分析 求10000之内的素数是一个常见的问题。素数是大于1且只能被1和自身整除的整数。我们可以使用循环遍历10000以内的每个数,判断其是否是素数。 方法1: 简单遍历法 遍历2到10000之间的每个数,判断其是否为素…...

ROS2 从头开始:第 5 部分 - 并发、执行器和回调组
一、说明 让我们回到基础。并发意味着系统或软件可以同时运行许多任务。例如,在单核 CPU 机器上,可以通过使用线程来实现并发。本文探讨了...
笔试强训Day3
学了一坤时Linux,赶紧来俩道题目放松放松。 T1:在字符串中找出连续最长的数字串 链接:在字符串中找出连续最长的数字串__牛客网 输入一个字符串,返回其最长的数字子串,以及其长度。若有多个最长的数字子串,…...

软考软件设计师-存储管理-文件管理-计算机网络(中
文章目录 一、存储管理页面置换算法 (最佳OPT)存储页面-先进先出置换算法(FIFO)最久未使用算法(最近最久未使用LRU) 二、文件管理初识文件管理文件目录-绝对路径文件管理-文件的结构文件管理-索引的分配 空闲存储空间的管理(位示图法)三、计算…...

Vue3的学习
create-vue创建vue3项目 create-vue是官方新的脚手架工具,底层切换到了vite(下一代构建工具),为开发提供急速响应 前提环境条件:控制面板输入node -v,显示的是安装了16.0或更高版本的Node.js创建一个Vue应…...
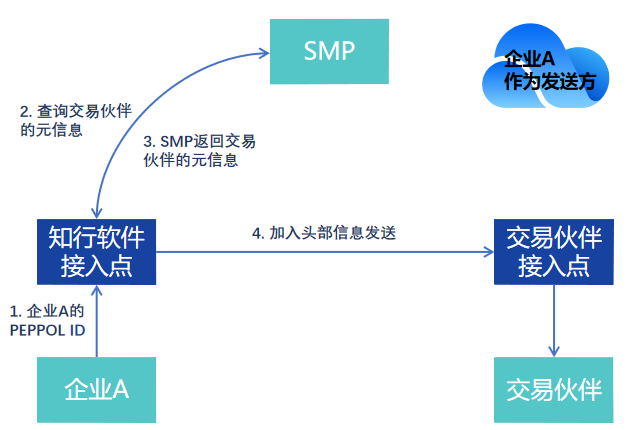
什么是Peppol ID?如何创建?
Peppol 网络的两大优势是安全和高效,由于Peppol 最常用于电子发票,因此这些优势在电子发票上展露无遗。相比之下,通过电子邮件发送 PDF 格式的发票和其他文件不仅处理成本较高,而且容易出现发票欺诈。 如果您所在的公共部门组织或…...

Spring注解大揭秘:@Component、@Service、@Repository详解
Spring注解大揭秘:Component、Service、Repository详解 前言比较 前言 想象一下,你正在构建一个复杂的Spring应用程序。你需要管理各种不同类型的组件,包括服务层、数据访问层和通用组件。Spring的Component、Service和Repository注解就像是你…...

Innodb底层原理与Mysql日志机制
MySQL内部组件结构 Server层 主要包括连接器、词法分析器、优化器、执行器等,涵盖 MySQL 的大多数核心服务功能,以及所有的内置函数(如日期、时间、数学和加密函数等),所有跨存储引擎的功能都在这一层实现,…...

浅谈大数据背景下用户侧用电数据在电力系统的应用与发展分析
安科瑞 华楠 摘要:随着能源互联网、互联网、新型传感技术的持续推进,电力用户侧用电数据呈现指数级剧增、异构性增强的情况,逐渐构成了用户侧用电行为大数据。然而目前对电力领域的数据价值挖掘于电网内部和电源端,用户侧庞大且蕴…...

20230919在WIN10下使用python3将PDF文档转为DOCX格式的WORD文档
20230919在WIN10下使用python3将PDF文档转为DOCX格式的WORD文档 2023/9/19 11:20 python pdf word https://blog.csdn.net/u013185349/article/details/130059657 Python实现PDF转Word文档 AcceptedLin 已于 2023-04-10 14:45:17 修改 1243 收藏 1 文章标签: pd…...

PCR检测试剂——博迈伦
PCR(聚合酶链式反应)是一种常用的分子生物学技术,被广泛应用于基因分型、基因表达分析、病原体检测等领域。在PCR实验中,PCR检测试剂是必不可少的重要组成部分,它们包括引物、酶、缓冲液和核苷酸。 1. 引物(…...
spring一个项目多个模块聚合打包问题解决方案
文章目录 1.问题描述:2.解决方案一、创建聚合父工程二、创建子模块(module)三、编写子模块代码1.模块1(demo-one)2.模块2(demo-tow) 四、创建聚合模块 (demo-starter)1. …...
何时被解析)
Linux设备树(Device Tree)何时被解析
Linux设备树(Device Tree)是在内核启动阶段就会被解析。当 Linux 内核启动的时候,它会读取设备树文件(dtb文件)并根据里面的信息来组织设备、加载驱动等。在驱动代码里,通常我们是在驱动初始化(…...
)
【Elasticsearch】数据简单操作(二)
简介:Elasticsearch(ES)是一个开源的分布式搜索和分析引擎,用于快速存储、搜索和分析大量数据。它具有高性能、可扩展性和灵活性的特点,被广泛用于构建实时搜索、日志分析、数据可视化等应用。 本文主要介绍ES索引的操…...

4 vCPU 实例达成 100 万 JSON API 请求/秒的优化实践
“性能工程” (Performance engineering)是个日渐流行的概念。顾名思义“性能工程”是包含在系统开发生命周期中所应用的一个技术分支,其目的就是确保满足非功能性的性能需求,例如:性能、可靠性等。由于现代软件系统变…...

呼叫中心系统有什么优势
在随着企业的管理水平也在不断提高。企业经营管理中所涉及到的各种复杂问题都有逐渐凸显出来。传统的呼叫中心已无法满足企业服务需求和客户满意度变化的要求。因此通过呼叫中心系统将企业业务流程和数据整合起来进行管理和运营已经成为目前企业管理领域中较为流行和成熟之选。…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

CSS 工具对比:UnoCSS vs Tailwind CSS,谁是你的菜?
在现代前端开发中,Utility-First (功能优先) CSS 框架已经成为主流。其中,Tailwind CSS 无疑是市场的领导者和标杆。然而,一个名为 UnoCSS 的新星正以其惊人的性能和极致的灵活性迅速崛起。 这篇文章将深入探讨这两款工具的核心理念、技术差…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...
