KNN-K近邻算法(K-Nearest Neighbors)
k近邻算法的特点
- 思想极度简单
- 应用数学知识少(近乎为零)
- 效果好(缺点?)
- 可以解释机器学习算法使用过程中的很多细节问题
- 更完整的刻画机器学习应用的流程
k近邻算法

k近邻算法整体是这样的一个算法,我们已经知道的这些数据点其实是分布在一个特征空间中的,通常呢,我们使用一个二维的平面来演示。比如说现在这个例子就是一个肿瘤病人相关的数据,横轴代表一个特征,是发现了这个肿瘤病人他肿块的大小,而纵轴呢,是发现这个肿块的时间。对于每一个病人,他的肿块大小和发现这个肿瘤的时间就构成了在这个特征平面中的一个点。这些点中有恶性的肿瘤用蓝色表示,良性的肿瘤用红色表示,图中一共有八个数据点。
如果现在新来的一个病人,他在特征空间中对应的位置在这里,我们怎么判断这个新来的绿色点,它最有可能是良性肿瘤患者还是恶性肿瘤患者呢?K近邻算法就是这样的一个算法,首先我们必须取一个K值,假设K等于三。对于每一个新的数据点,K近邻算法做的事情就是在所有的这些点中寻找离这个新的点最近的三个点。然后这些最近的点以他们自己的label,自己的结果进行投票。在这个例子中,离这个新的点最近的三个点都是代表恶性肿瘤的蓝色的点,所以蓝色对红色是3:0。因此K近邻算法就说这个新的点有很高的概率,它其实也是一个蓝色的点,很有可能是一个恶性肿瘤的患者。


K近邻算法的本质是认为两个样本如果他们足够的相似的话,那么它就有更高的概率属于同一个类别。当然可能只看离它最近的那一个样本是不靠谱的,所以我们多看几个样本,一共看K个样本,看哪个类别最多,我们就认为这个新的样本最有可能属于哪个类别, 可以理解为少数服从多数。
在这里,我们描述两个样本是否相似,这个相似性是通过两个样本在特征空间中的距离来进行描述的。
我们再举一个例子, 比如现在又新来了一个病人

我们来看一下离它最近的三个点, 那么对于这个新来的点, 红色和蓝色的比率时候2:1, 所以红色胜出, 我们来看一下离它最近的三个点, 那么对于这个新来的点, 红色和蓝色的比率时候2:1, 所以红色胜出, 那么K近邻算法就告诉我们,对于这个新病人来说, 他更可能是一个良性肿瘤患者
k近邻算法首先可以解决的是我们之前介绍的监督学习分类的问题, 不过k近邻算法也可以解决回归问题, 后续我们将进行介绍
计算距离我们使用欧拉距离公式:
欧拉距离
( x ( a ) − x ( b ) ) 2 + ( y ( a ) − y ( b ) ) 2 ( x ( a ) − x ( b ) ) 2 + ( y ( a ) − y ( b ) ) 2 + ( z ( a ) − z ( b ) ) 2 ( X 1 ( a ) − X 1 ( b ) ) 2 + ( X 2 ( a ) − X 2 ( b ) ) 2 + … + ( X n ( a ) − X n ( b ) ) 2 \begin{array}{c}\sqrt{\left(x^{(a)}-x^{(b)}\right)^{2}+\left(y^{(a)}-y^{(b)}\right)^{2}} \\\sqrt{\left(x^{(a)}-x^{(b)}\right)^{2}+\left(y^{(a)}-y^{(b)}\right)^{2}+\left(z^{(a)}-z^{(b)}\right)^{2}} \\\sqrt{\left(X_{1}^{(a)}-X_{1}^{(b)}\right)^{2}+\left(X_{2}^{(a)}-X_{2}^{(b)}\right)^{2}+\ldots+\left(X_{n}^{(a)}-X_{n}^{(b)}\right)^{2}}\end{array} (x(a)−x(b))2+(y(a)−y(b))2(x(a)−x(b))2+(y(a)−y(b))2+(z(a)−z(b))2(X1(a)−X1(b))2+(X2(a)−X2(b))2+…+(Xn(a)−Xn(b))2
第二个公式是欧拉距离公式在立体几何中的拓展
不过对于我们要处理的这个特征向量很有可能要比三维要高,那么此时我们使用这种XYZ一个一个的字母是不方便的所以在这里我们又添加了一个角标,X就是代表我们整个的数据, x n ( a ) {x_{n}}^{(a)} xn(a)就代表a样本的第n个维度, x n ( b ) {x_{n}}^{(b)} xn(b)就代表b样本的第n个维度, 那么这个式子其实就是在计算ab两个样本之间的距离, 这个计算方式就是A样本的每个维度的特征减去B样本中相应的每个维度的特征然后平方然后进行相加最后再开个根号, 在公式中我们假设我们的特征向量一共有N个维度, 也就是说一共有n个特征。这就是高维的欧拉距离公式的计算
但是这种公式看起来比较不方便, 所以通常我们使用连加的形式来进行表示
∑ i = 1 n ( X i ( a ) − X i ( b ) ) 2 \sqrt{\sum_{i=1}^{n}\left(X_{i}^{(a)}-X_{i}^{(b)}\right)^{2}} i=1∑n(Xi(a)−Xi(b))2
它表示从i=1开始, 直到i=n结束, 每次都将A样本的第i个特征和B样本的第i个特征相减再平方, 最后所有的项加起来开个根号
接下来我们先采用最原始的方式实现一下KNN分类算法, 先大致的了解一下KNN算法的实现思路(以下代码均在jupyter 中实现)
在此之前我们先使用matplotlib库可视化一下数据集中的数据
import numpy as np
import matplotlib.pyplot as plt
raw_data_X = [[3.393533211, 2.331273381],[3.110073483, 1.781539638],[1.343808831, 3.368360954],[3.582294042, 4.679179110],[2.280362439, 2.866990263],[7.423436942, 4.696522875],[5.745051997, 3.533989803],[9.172168622, 2.511101045],[7.792783481, 3.424088941],[7.939820817, 0.791637231]]# 每一个样本的类别, 0代表良性肿瘤, 1代表恶性肿瘤
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
# 将所有的数据都作为我们的训练集
# 在这里我们进行命名训练集, 也就是对应的是训练使用的这些样本的label
X_train = np.array(raw_data_X)
y_train = np.array(raw_data_y)
X_train
array([[3.39353321, 2.33127338],[3.11007348, 1.78153964],[1.34380883, 3.36836095],[3.58229404, 4.67917911],[2.28036244, 2.86699026],[7.42343694, 4.69652288],[5.745052 , 3.5339898 ],[9.17216862, 2.51110105],[7.79278348, 3.42408894],[7.93982082, 0.79163723]])
y_train
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
# 进行可视化我们训练的样本
plt.scatter(X_train[y_train==0, 0], X_train[y_train==0, 1], color="g")
plt.scatter(X_train[y_train==1, 0], X_train[y_train==1, 1], color="r")
plt.show()

# 假设新输入一个数据
x = np.array([8.093607318, 3.365731514])
# 进行可视化我们训练的样本
plt.scatter(X_train[y_train==0, 0], X_train[y_train==0, 1], color="g")
plt.scatter(X_train[y_train==1, 0], X_train[y_train==1, 1], color="r")
plt.scatter(x[0], x[1], color="b")
plt.show()

KNN的过程
from math import sqrt
# 原始方法(笨方法)
# 该列表是用于存储它们之间的距离
distances = []
for x_train in X_train:d = sqrt(np.sum((x_train - x)**2))# 让两个样本进行对应相减得到两点之间的距离distances.append(d)
distances
[4.812566907609877,5.229270827235305,6.749798999160064,4.6986266144110695,5.83460014556857,1.4900114024329525,2.354574897431513,1.3761132675144652,0.3064319992975,2.5786840957478887]
nearest = np.argsort(distance)
# 查看训练数据集中离新输入的患者最近的几个点
nearest
array([8, 7, 5, 6, 9, 3, 0, 1, 4, 2], dtype=int64)
在 k-最近邻(k-Nearest Neighbors,简称 k-NN)算法中,“k” 指的是一个超参数,表示用于确定新样本所属类别的邻居数量。具体来说,k-NN 算法通过以下步骤来进行分类:
- 计算未知样本与训练集中所有已知样本的距离。
- 选择距离最近的 “k” 个已知样本(最近的 k 个邻居)。
- 根据这 k 个邻居中所属类别的多数投票来确定未知样本的类别。换句话说,未知样本将被分类为与其距离最近的 k 个邻居中最常见的类别。
因此,k-NN 算法中的 “k” 控制了决策过程中邻居的数量,它是一个重要的超参数,需要根据具体问题的特点来选择。选择不同的 “k” 值可能会导致不同的分类结果,因此通常需要进行交叉验证等方法来确定最佳的 “k” 值。较小的 “k” 值可能会导致模型对噪声敏感,而较大的 “k” 值可能会导致模型过于平滑。因此,在实际应用中,需要根据数据集的特点和问题的需求来选择合适的 “k” 值。
# k 指的是要查找的最近样本的数量
k=6
# 查找最近的点相应的y坐标
topk_y = [y_train[i] for i in nearest[:k]]
topk_y
[1, 1, 1, 1, 1, 0]
接下来我们看下collections中的Counter方法
collections 模块是 Python 标准库中的一个模块,它提供了一些额外的数据类型和数据结构,用于扩展内置数据类型(如列表、元组、字典等)的功能。Counter 是 collections 模块中的一个类,用于创建计数器对象,用于计算可迭代对象中元素的出现次数。
以下是关于 Counter 类的一些详细信息和用法示例:
-
创建计数器对象:可以使用
Counter()构造函数来创建一个计数器对象。计数器对象可以接受一个可迭代对象作为参数,例如列表、字符串、元组等。from collections import Counter# 创建计数器对象 my_list = [1, 2, 2, 3, 3, 3, 4, 4, 4, 4] counter = Counter(my_list)print(counter)输出:
Counter({4: 4, 3: 3, 2: 2, 1: 1})上面的计数器对象表示在
my_list中,元素 4 出现了 4 次,元素 3 出现了 3 次,以此类推。 -
元素计数:可以使用计数器对象的键(元素)来查询元素出现的次数。
print(counter[3]) # 查询元素 3 出现的次数输出:
3 -
元素计数的方法:计数器对象还提供了一些方法来获取元素的计数。
print(counter.get(2)) # 获取元素 2 出现的次数 print(counter.keys()) # 获取所有不重复的元素 print(counter.values()) # 获取所有元素的计数值 print(counter.most_common()) # 获取按计数值降序排列的元素列表 -
更新计数器:可以使用计数器对象的
update()方法来更新计数器的内容。counter.update([3, 4, 5]) # 更新计数器,增加元素 5 的计数更新后的计数器会反映新的计数值。
Counter 类在数据分析、文本处理和统计分析等领域非常有用,它可以帮助你快速统计和分析数据中元素的出现频率。
from collections import Counter# 我们可以把这个统计的过程理解成投票vote的过程
Counter(topk_y) # 它会自动统计距离这个新输入样本最近的7个样本中不同类别所占的个数, 返回值是个字典类型的数据
Counter({1: 5, 0: 1})
votes = Counter(topk_y)
votes.most_common(1)[0][0] # 括弧中的数字代表票数最多的几个元素, 返回值是一个元素为元组的列表
1
predict_y = votes.most_common(1)[0][0] # 这就是整个预测出来的值
相关文章:

KNN-K近邻算法(K-Nearest Neighbors)
k近邻算法的特点 思想极度简单应用数学知识少(近乎为零)效果好(缺点?)可以解释机器学习算法使用过程中的很多细节问题更完整的刻画机器学习应用的流程 k近邻算法 k近邻算法整体是这样的一个算法,我们已经知道的这些数据点其实是…...

ChatGPT:理解HTTP请求数据格式:JSON、x-www-form-urlencoded和form-data
ChatGPT:理解HTTP请求数据格式:JSON、x-www-form-urlencoded和form-data 使用postman发送一个post请求,在body里面加上了form-data数据,namexxx,age23,为什么输出request.body()得到的是这样的结果 -------…...

字符集、IO流(一)
字符集、IO流(一) 各位同学,前面我们已经学习了File类,通过File类的对象可以对文件进行操作,但是不能操作文件中的内容。要想操作文件中的内容,我们还得学习IO流。但是在正式学习IO流之前,我们还需要学习一个前置知识叫做字符集,只有我们把字符集搞明白了,再学习IO流…...
)
相乘(蓝桥杯)
相乘 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小蓝发现,他将 1 至 1000000007 之间的不同的数与 2021 相乘后再求除以 1000000007 的余数,会得到不同的数。 小蓝想知道,能不能在 1 …...
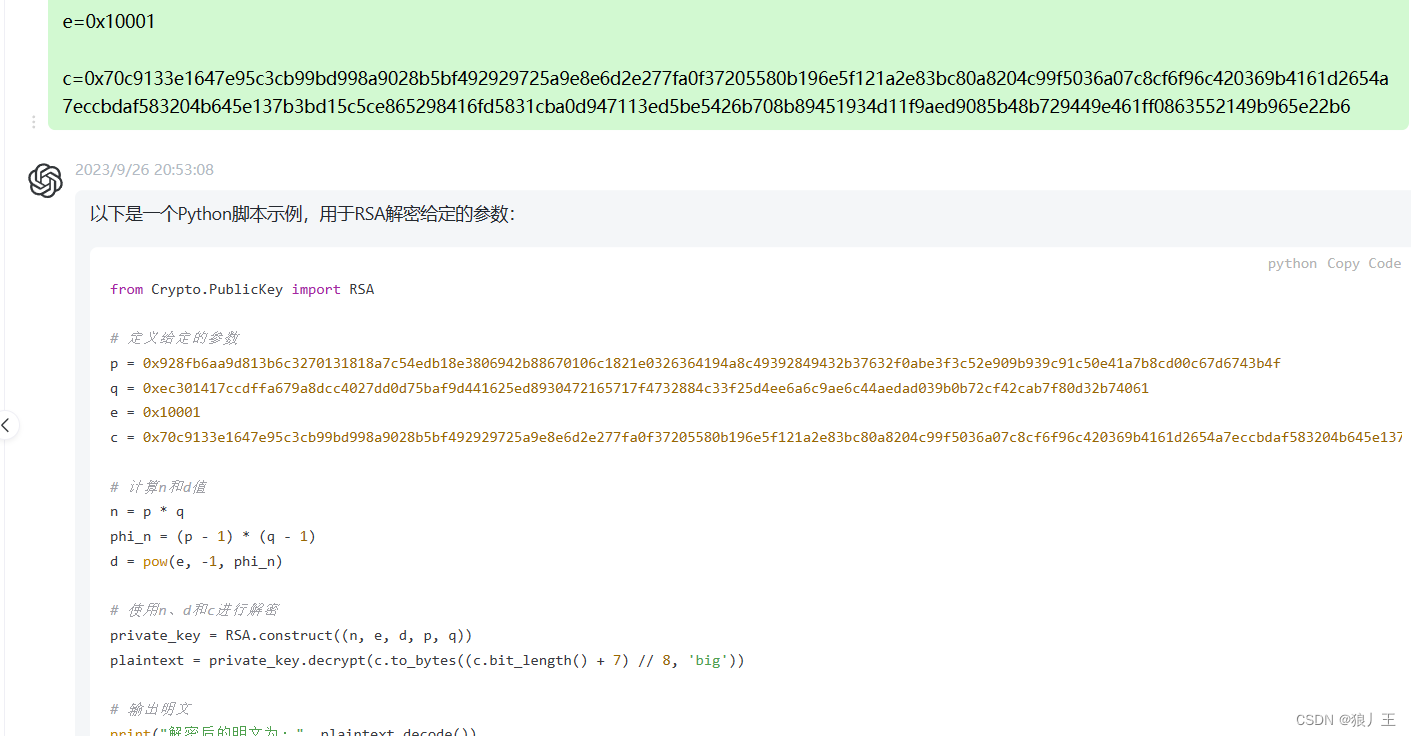
[AFCTF 2018]你能看出这是什么加密么
最开始是我对rsa的小小的理解 rsa也就是非对称加密算法,拥有公开的加密密钥和解密密钥,这也是我们写脚本的基础 选取素数p和q,计算乘积npq,以及(n)(p-1)(q-1)。(欧拉函数) 选择一个e值作为密钥…...
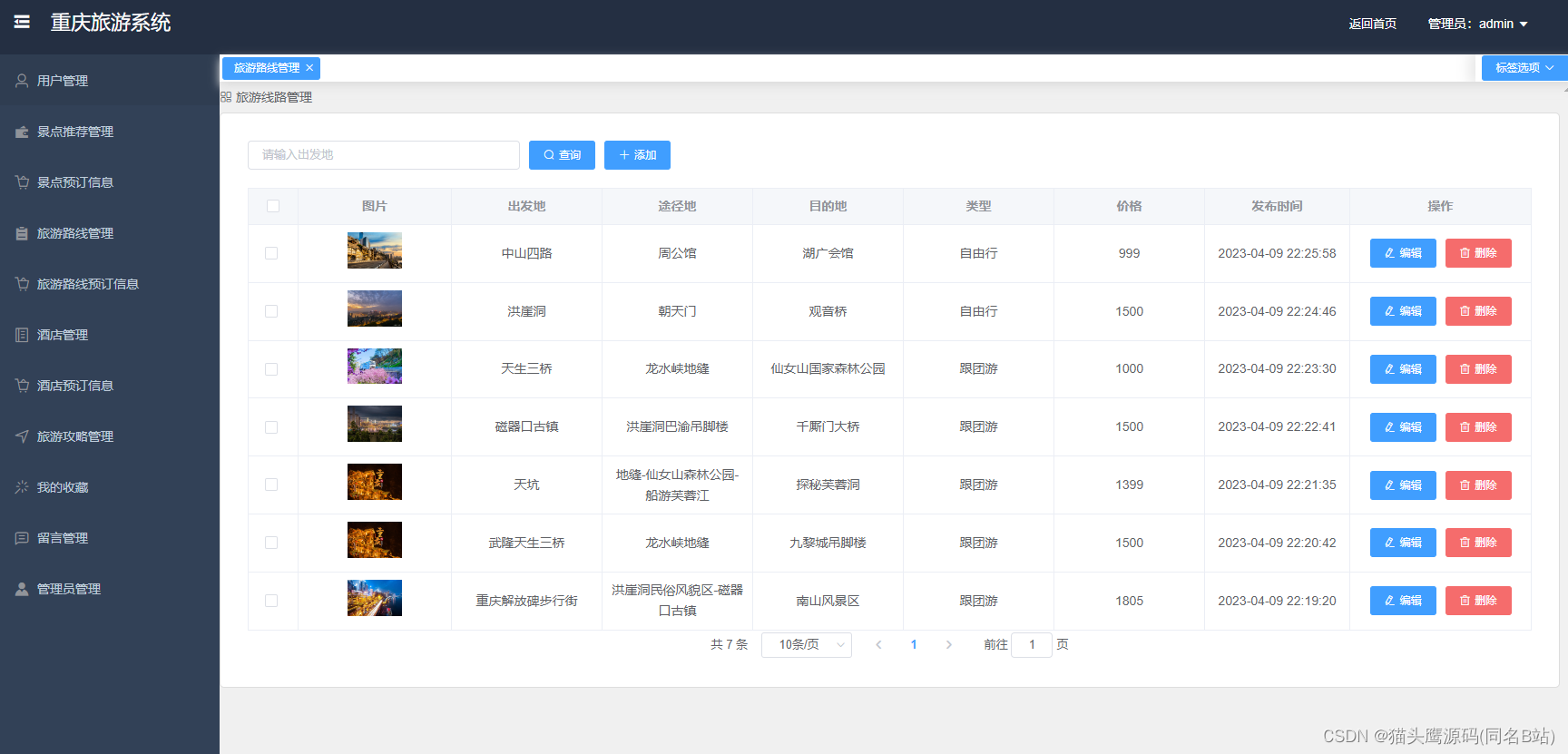
基于springboot+vue的重庆旅游网(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

pymysql执行delete删除操作
视频版教程 Python操作Mysql数据库之pymysql模块技术 执行delete操作,雷同前面的update操作 from pymysql import Connectioncon Nonetry:# 创建数据库连接con Connection(host"localhost", # 主机名port3306, # 端口user"root", # 账户…...

25862-2010 制冷与空调用同轴套管式换热器
声明 本文是学习GB-T 25862-2010 制冷与空调用同轴套管式换热器. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本标准规定了制冷与空调用同轴套管式换热器(以下简称"换热器")的术语和定义、基本参数、要 求、试验、检验规则、标…...

JetBrains 产品安装插件(plugins)的两种方式
安装分为在线、离线两种方式: 在线方式: File > Settings > Plugins 搜索插件 Install 即可 离线方式: 官网:https://plugins.jetbrains.com/ 搜索到插件后,点击 "Get",选择自己安装的…...
SOLIDWORKS二次开发
SOLIDWORKS是一套三维设计软件, 采用特征建模、变量化驱动可方便地实现三维建模、装配和生成工程图。SOLIDWORKS软件本身所具有的交互方式,可以使用户对已生成模型的尺寸、几何轮廓和相互约束关系随时进行修改, 而不需要编程。SOLIDWORKS软件本身的方程式可以实现简…...

Linux下压缩和解压缩
在Linux下,您可以使用多种命令来进行文件和目录的压缩和解压缩操作。以下是一些常见的压缩和解压缩命令: tar:tar命令可用于创建和提取tar压缩文件。例如,要创建一个名为archive.tar的.tar文件,可以使用以下命令&#…...

爬虫入门基础-HTTP协议过程
在进行网络爬虫开发之前,了解HTTP协议的基本过程是非常重要的。HTTP协议是Web通信的基础,也是爬取网页数据的核心。本文将为您详细介绍HTTP协议的过程,帮助您理解爬虫背后的网络通信机制。让我们一起来探索吧! 一、什么是HTTP协议…...

数据结构 第一章作业 绪论 西安石油大学
绪论第1章 1.简述下列概念:数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。 答案: 数据:是客观事物的符号表示,指所有能输入到计算机中并被计算机程序处理的符号的总称。如数学计…...
HTML5福利篇--使用Canvas画图
目录 一.Canvas元素 1.Canvas元素定义 2.使用JavaScript获取页面中的Canvas对象 二.绘制图形 1.绘制直线 2.绘制矩形 (1)rect() (2)strokeRect() (3)fillRect()和clearRect()函数 3.绘制圆弧 4.…...

基于Matlab实现图像目标边界描述
图像目标边界描述是图像处理中的一个重要问题。边界描述可以用于目标检测和识别、图像分割等应用。Matlab提供了强大的图像处理工具箱,可以方便地实现图像目标边界描述。本文介绍一种基于边缘检测的图像目标边界描述方法,并提供一个简单的案例源码。 文章…...

汽车电子——产品标准规范汇总和梳理(自动驾驶)
文章目录 前言 一、分级 二、定位 三、地图 四、座舱 五、远程 六、信息数据 七、场景 八、智慧城市 九、方法论 总结 前言 见《汽车电子——产品标准规范汇总和梳理》 一、分级 《GB/T 40429-2021 汽车驾驶自动化分级》 《QC/T XXXXX—XXXX 智能网联汽车 自动驾…...
redis部署与管理
目录 一、关系数据库与非关系型数据库: 1. 关系型数据库: 2.非关系型数据库: 二、关系型数据库和非关系型数据库区别: (1)数据存储方式不同: (2)扩展方式不同…...

MySQL 事件
文章目录 1.简介2.事件调度器3.创建事件4.查看事件5.修改事件6.删除事件参考文献 1.简介 MySQL 事件(Event)事件是根据时间表运行的任务,类似于 Unix crontab 和 Windows 定时任务。 一个事件可调用一次,也可周期性地启动。它由…...
软件项目费用计算方法
计算软件项目的费用是项目管理的关键组成部分之一。费用计算方法可以帮助您确定项目的总成本,包括开发、测试、维护和其他相关费用。以下是一些常见的软件项目费用计算方法,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发…...
暗月中秋靶场活动writeup
前言 暗月在中秋节搞了个靶场活动,一共有4个flag,本着增长经验的想法参加了本次活动,最终在活动结束的时候拿到了3个flag,后面看了其他人的wp也复现拿到第四个flag。过程比较曲折,所以记录一下。 靶场地址 103.108.…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

