统计的基本概念及抽样分布
文章目录
- 🍋引言
- 🍋总体(Population)
- 🍋总体参数
- 🍋样本(Sample)
- 🍋随机样本
- 🍋样本统计量
- 🍋统计量(Statistic)
- 🍋样本均值(Sample Mean)
- 🍋样本方差和标准差(Sample Variance and Standard Deviation)
- 🍋常用分布和分位点
- 🍋1. 正态分布(Normal Distribution)
- 🍋2. t分布(t-distribution)
- 🍋3. χ²分布(Chi-Squared Distribution)
- 🍋统计学中的应用
- 🍋单个正态总体的抽样分布
- 🍋两个正态总体的抽样分布
🍋引言
统计学作为一门重要的科学领域,涵盖了众多的概念和方法。本文将重点介绍统计学的基本概念,包括总体、样本以及统计量,并将通过数学公式来解释它们之间的关系。
🍋总体(Population)
总体是我们感兴趣的全体对象或观察单元的集合。在统计学中,总体可以包括人口、产品、事件等等。总体通常用大写字母N表示,总体的某一属性通常用大写字母X表示。例如,总体平均值用μ表示,总体标准差用σ表示。
🍋总体参数
总体的属性可以通过各种参数来描述。例如,总体的均值、方差、标准差等都是描述总体性质的参数。这些参数通常是未知的,我们的目标是通过样本数据对它们进行估计。
🍋样本(Sample)
由于通常不可能获取总体的全部数据,我们使用样本来代表总体。样本是总体中的一个子集,通常用小写字母n表示样本大小。样本的属性通常用小写字母x表示,例如样本均值用x̄表示。
🍋随机样本
为了保证结果的代表性,样本需要是随机抽取的,这意味着每个总体成员被选中的概率应该是相等的。
🍋样本统计量
样本统计量是从样本中计算出来的数值,用来估计总体参数。最常见的样本统计量包括样本均值、样本方差和样本标准差。这些统计量通常用帽子符号(^)表示,例如样本均值用x̄表示,样本标准差用s表示。
🍋统计量(Statistic)
统计量是从样本数据计算出来的数值,用于对总体参数进行估计。统计量可以是点估计或区间估计。
🍋样本均值(Sample Mean)
样本均值是样本中所有数据值的平均数,它通常用以下公式表示:
x̄ = (Σxi) / n
其中,x̄表示样本均值,Σxi表示所有样本数据的总和,n表示样本大小。
🍋样本方差和标准差(Sample Variance and Standard Deviation)
样本方差是样本数据偏离均值的平方和的平均值,它通常用以下公式表示:
s² = Σ(xi - x̄)² / (n - 1)
样本标准差则是样本方差的平方根,它通常用以下公式表示:
s = √(Σ(xi - x̄)² / (n - 1))
其中,s²表示样本方差,s表示样本标准差,xi表示样本中的每个数据点,x̄表示样本均值,n表示样本大小。
🍋常用分布和分位点
在统计学中,有一些常用的概率分布,它们用于描述不同类型的数据分布。这些分布在许多统计分析中都起着重要作用。本文将介绍一些常见的分布,包括正态分布、t分布和卡方分布,并讨论分位点的概念。
🍋1. 正态分布(Normal Distribution)
正态分布也被称为高斯分布,它是最常见的概率分布之一。正态分布的概率密度函数(Probability Density Function,PDF)如下:

其中,xx 表示随机变量的取值,μμ 是均值,σσ 是标准差。正态分布是钟形曲线,均值位于分布的中心,标准差决定了曲线的宽度。
正态分布的分位点
正态分布的分位点是指分割概率分布的数值,通常以 zz 表示。正态分布的分位点可以用来计算概率或查找给定概率下的值。例如,第 αα 个百分位点(Percentile)表示在正态分布中,有 αα 的概率小于或等于该值。正态分布的分位点通常用 zαzα 表示,可以通过查找标准正态分布表格或计算得到。
🍋2. t分布(t-distribution)
t分布是用于小样本中的统计推断的分布,它更广泛地适用于总体标准差未知的情况。t分布的PDF为:
f ( t ) = ( Γ ( ( ν + 1 ) / 2 ) / ( s q r t ( ν π ) ∗ Γ ( ν / 2 ) ) ) ∗ ( 1 + ( t 2 / ν ) ) ( − ( ν + 1 ) / 2 ) f(t) = (Γ((ν+1)/2) / (sqrt(νπ) * Γ(ν/2))) * (1 + (t²/ν))^(-(ν+1)/2) f(t)=(Γ((ν+1)/2)/(sqrt(νπ)∗Γ(ν/2)))∗(1+(t2/ν))(−(ν+1)/2)
其中,f(t)表示在t处的概率密度,ν表示自由度,Γ表示伽马函数。
分位点: t分布的分位点与自由度有关。例如,t分布的95%置信水平的上下分位点对应于自由度为n-1时,使得在这两个点之间的面积为0.95。
🍋3. χ²分布(Chi-Squared Distribution)
χ²分布是用于分析卡方检验和构建置信区间的分布。它的PDF为:
f ( x ) = ( 1 / ( 2 ( k / 2 ) ∗ Γ ( k / 2 ) ) ) ∗ x ( k / 2 − 1 ) ∗ e ( − x / 2 ) f(x) = (1 / (2^(k/2) * Γ(k/2))) * x^(k/2 - 1) * e^(-x/2) f(x)=(1/(2(k/2)∗Γ(k/2)))∗x(k/2−1)∗e(−x/2)
其中,f(x)表示在x处的概率密度,k表示自由度,Γ表示伽马函数。
分位点: χ²分布的分位点同样与自由度有关。例如,χ²分布的95%置信水平的上下分位点对应于自由度为k时,使得在这两个点之间的面积为0.95。
🍋统计学中的应用
这些常用分布和分位点在统计学中有广泛的应用。例如,正态分布用于描述许多自然现象,t分布用于小样本中的参数估计和假设检验,χ²分布用于分析离散型数据。分位点帮助我们计算概率、构建置信区间和进行假设检验,是统计学中不可或缺的工具。
总之,了解这些常用分布和分位点有助于我们更好地理解数据的分布特征,进行准确的统计分析,做出科学的决策。这些概念和数学工具为数据科学、经济学、医学研究等领域提供了坚实的基础。
🍋单个正态总体的抽样分布
正态总体
首先,让我们简要介绍一下单个正态总体。正态总体(或称为正态分布总体)是一种连续概率分布,通常由其均值(μ)和标准差(σ)来描述。正态分布总体的概率密度函数(PDF)如下:

单个正态总体的抽样分布
抽样分布是从一个总体中抽取多个样本,并计算每个样本的统计量(如样本均值)的分布。对于单个正态总体,如果我们从中抽取多个大小为 n 的随机样本,并计算每个样本的均值,那么这些样本均值的分布将近似于正态分布。这个近似性质可以通过中心极限定理来解释。
中心极限定理指出,当样本容量足够大时,这些样本均值的抽样分布将近似于正态分布,其均值等于总体均值 μ,标准差等于总体标准差 σ 除以 √n。这可以表示为:
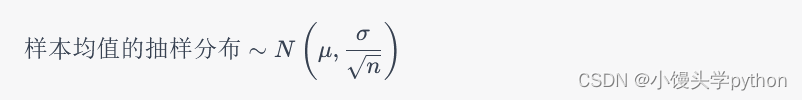
这个结果对于统计推断非常重要,因为它允许我们使用正态分布的性质来进行置信区间估计和假设检验,即使我们不知道总体的分布形状。
🍋两个正态总体的抽样分布
两个正态总体
现在,让我们考虑两个正态总体的情况。假设我们有两个独立的正态分布总体,分别具有均值 μ1 和 μ2,标准差 σ1 和 σ2。我们想要了解两个总体之间是否存在显著差异。
两个正态总体的抽样分布
当我们从两个正态总体中分别抽取两组样本,并计算这两组样本的差异(通常是均值之差)时,差异的抽样分布遵循一个特殊的分布,称为 t 分布。
具体来说,如果我们有两个独立的样本,每个样本大小为 n1 和 n2,且这两个样本分别来自两个正态总体,那么这两个样本均值之差的抽样分布近似于 t 分布。这个 t 分布的均值等于两个总体均值之差(μ1 - μ2),标准差由公式给出:
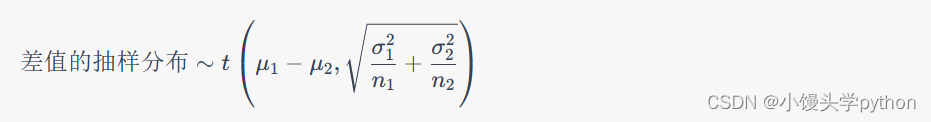
这个 t 分布在假设检验中经常用于比较两个总体均值是否有显著差异。通常,我们计算 t 统计量并与 t 分布的临界值进行比较,以确定是否拒绝假设。
总结起来,单个正态总体的抽样分布基于中心极限定理近似为正态分布,而两个正态总体的抽样分布涉及 t 分布,用于比较两个总体的均值差异。这些概念在统计学中是非常重要的,它们为数据分析和统计推断提供了强大的工具。

挑战与创造都是很痛苦的,但是很充实。
相关文章:

统计的基本概念及抽样分布
文章目录 🍋引言🍋总体(Population)🍋总体参数 🍋样本(Sample)🍋随机样本🍋样本统计量 🍋统计量(Statistic)🍋…...
this指针)
【C++】class的设计与使用(四)this指针
this指针 this作用域是在类内部,只能在成员函数中使用;this在成员函数的开始前构造,在成员函数的结束后清除;编译器在编译的时候也会自动加上this,它作为非静态成员函数的隐含形参,对各成员的访问均通过th…...
mysql 导入sql文件
mysql 导入sql文件 sudo mysql -uroot -p123456 -h127.0.0.1 sudo mysql -uroot -p123456 -h127.0.0.1然后 show databases;然后 use 数据库名称; 然后 source 20230920031001.sql;如果不加 -h127.0.0.1 可能会出现错误 /var/lib/mysql.sock error 通过 navicat导入的话&am…...

springcloud:三、ribbon负载均衡原理+调整策略+饥饿加载
Ribbon负载均衡原理 调整Ribbon负载均衡策略 第一种会对order-service里所有的服务消费者都采用该新规则 第二种会针对order-service里某个具体的服务消费者采用该新规则 饥饿加载...

【Unity编辑器扩展】Tranform组件自定义扩展,复制位置旋转缩放数据
目录 一、Tranform组件数据的扩展 二、 RectTransform组件数据的扩展 很多时候我们在做Tranform属性配置的时候需要反复的获取对象的位置信息,旋转信息。这个时候有个方便的工具会使得我们的效率大大提升。 一、Tranform组件数据的扩展 1.可以复制世界坐标,世界旋转 V…...

自动驾驶领域中的CMS系统应用探讨
由佐思汽研主办的“ ICVS汽车智能网联大会”正式启幕,邀请Tier1、软件供应商、操作系统商、智能驾驶及智能驾舱相关企业,共同探讨行业现状、创新技术应用交流、以及未来行业发展趋势等。 赛格导航视频产品线总监刘玉龙应邀参加本次大会,并发…...

十分钟理解OSPF路由协议
十分钟理解OSPF路由协议 1.RIP的缺陷以跳数为度量值最大跳数为15更新路由表采用全更新收敛速度慢 2.RIP与OSPF比较OSPF概述运行OSPF协议之前运行OSPF协议之后 3.OSPF协议工作过程1.发现邻居2.建立邻接关系3.传递链路状态信息4.计算路由 4.OSPF分区域管理 有RIP协议,…...

Python 编程基础 | 第一章-预备知识 | 1.4、包管理工具
一、包管理工具 1、pip简介 pip是Python自带的包管理器,它可以帮助我们安装、升级和卸载Python包。Python包是一组Python模块,它们可以提供各种功能,例如数据分析、Web开发、机器学习等等。pip可以让我们轻松地安装这些包,以便我…...
delphi中使用CADVCL 10.0 Enterprise控件解析DXF文件生成图片保存到本地
使用案例demos中GettingStarted案例 修改OnClick方法 更换代码 varvDrawing: TsgCADDXFImage;I: Integer;vEnt: TsgDXFEntity;vDXFImage:TsgCADImage;Bitmap: TBitmap;jpg: TJpegImage; beginvDrawing : TsgCADDXFImage.Create;vDrawing.LoadFromFile(d:\Entities.dxf);for …...
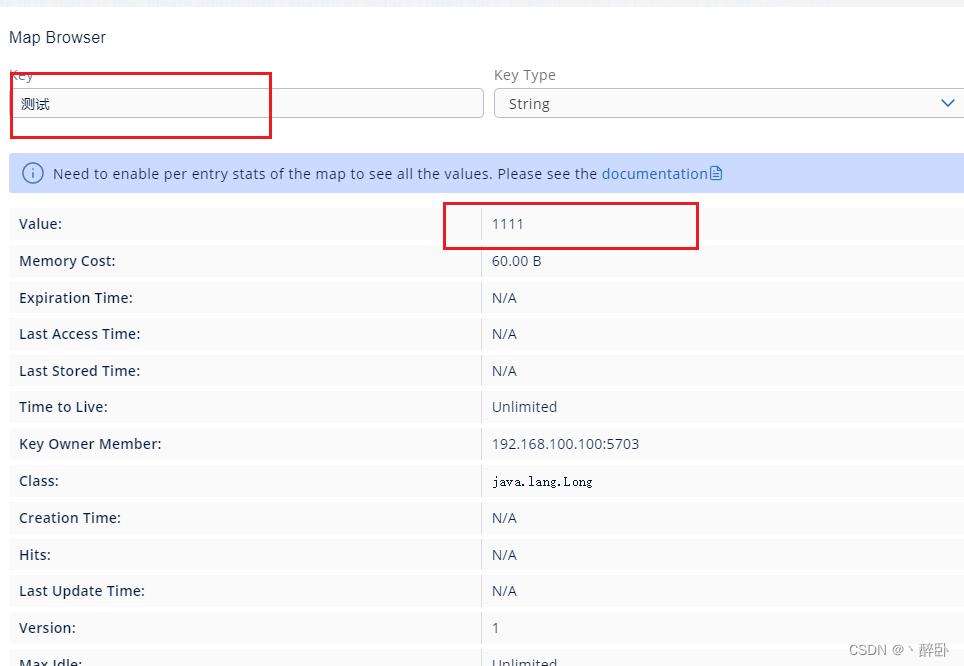
Hazelcast系列(三):hazelcast管理中心
系列文章 Hazelcast系列(一):初识hazelcast Hazelcast系列(二):hazelcast集成 Hazelcast系列(三):hazelcast管理中心 目录 前言 平台搭建 测试 其他 参考 总结 前言 前面,我们通过几种配置方式(Hazelcast系…...
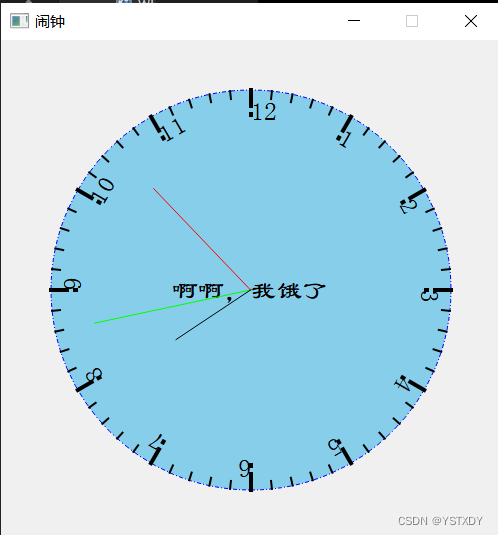
QT 绘画功能的时钟
.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPaintEvent> #include <QDebug> //信息调试类 #include <QPainter> #include <QPixmap> //图像引擎类 #include <QTime> #include <QTimer> …...
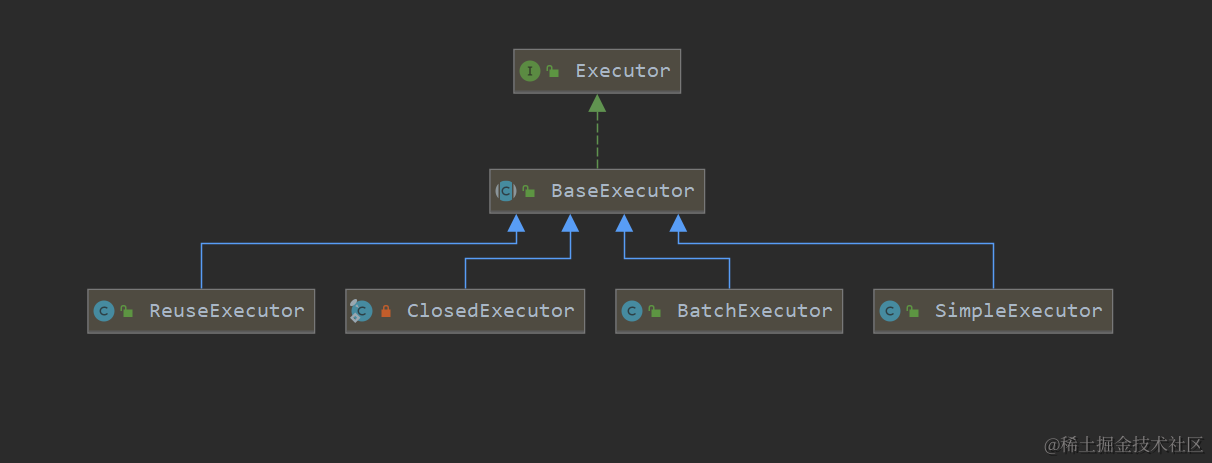
设计模式之道-模板方法模式
文章目录 模板方法模式简介作用模板方法模式的缺点模板方法模式的应用场景业务场景开源框架中的应用 对比回调和Hook模式关于组合优先于继承 关于设计模式乱用的现象 模板方法模式 简介 模板方法模式是一种行为型设计模式,该设计模式的核心在于通过抽象出一套相对…...

头哥的实践平台的Linux文件/目录管理
一 Linux 文件/目录管理 1.本关的编程任务是补全右侧代码片段中Begin至End中间的代码,具体要求如下: 新创建两个文件空文件file1和file2。 删除系统已存在的两个文件oldFile1和oldFile2。 #!/bin/bash#在以下部分写出完成任务的命令 #***********begi…...
软件测试基本常识
【软件测试面试突击班】如何逼自己一周刷完软件测试八股文教程,刷完面试就稳了,你也可以当高薪软件测试工程师(自动化测试) 一、测试用例的编写 1.在测试中最重要的文档,他是测试工作的核心,是一组在测试时…...
Xmake v2.8.3 发布,改进 Wasm 并支持 Xmake 源码调试
Xmake 是一个基于 Lua 的轻量级跨平台构建工具。 它非常的轻量,没有任何依赖,因为它内置了 Lua 运行时。 它使用 xmake.lua 维护项目构建,相比 makefile/CMakeLists.txt,配置语法更加简洁直观,对新手非常友好&#x…...
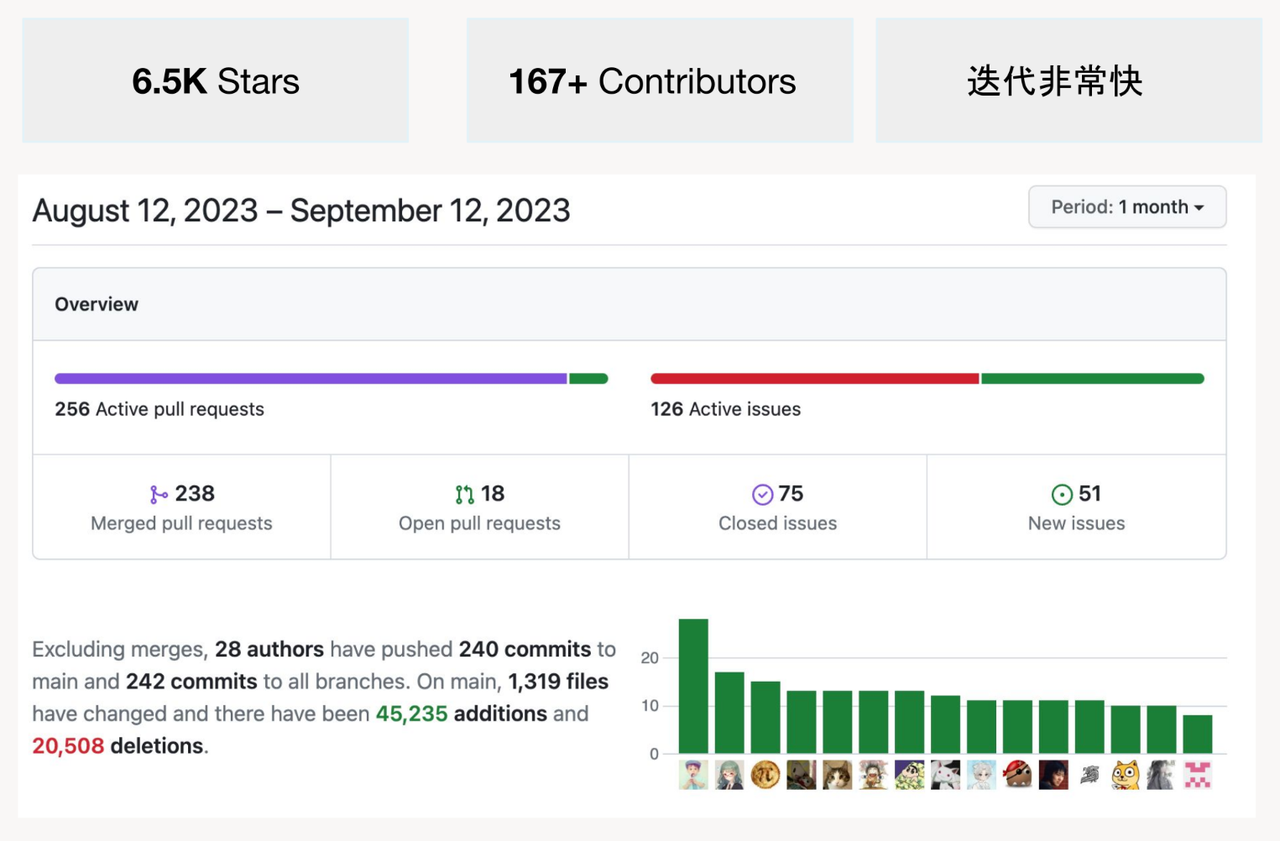
Serverless 数仓技术与挑战(内含 PPT 下载)
近期,Databend Labs 联合创始人张雁飞发表了题为「Serverless 数仓技术与挑战」的主题分享。以下为本次分享的精彩内容: 主题: 「Serverless 数仓技术与挑战」 演讲嘉宾: 张雁飞 嘉宾介绍: Databend Labs 联合创始人…...

九牧小牧携手国家队!一场“中国卫浴“和“中国体育”的双向奔赴
文 | 螳螂观察 作者 | 余一 1990年中国第一次举办了综合性国际体育大赛——北京亚运会,来自37个国家和地区,共计6578人的体育代表团参加了那届亚运会,一首《亚洲雄风》成为无数人记忆中的经典。 2023年杭州亚运会于近日正式拉开了帷幕&…...

crypto:Quoted-printable
题目 解压文件后可得到提示文本 好了这个没接触过,参考别的大佬wp QP为可打印字符编码,根据加密方式任何一个8位的字节值可编码为3个字符:一个等号“”后跟随两个十六进制数字(0–9或A–F)表示该字节的数值。 利用网…...

【六级】作文模板-议论文-问题解决
视频来源: https://www.bilibili.com/video/BV1vK4y1e7A6/?spm_id_from333.880.my_history.page.click&vd_sourcefb8dcae0aee3f1aab700c21099045395 1、前言 两类作文: 议论文 (how to 问题解决型) what 某种现象 漫画 &…...
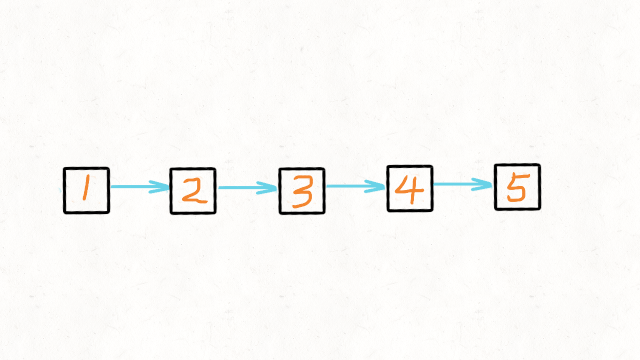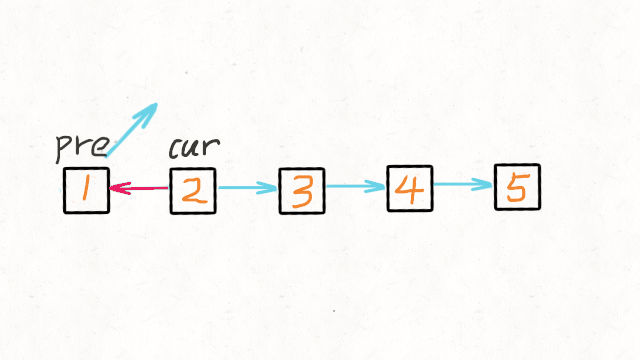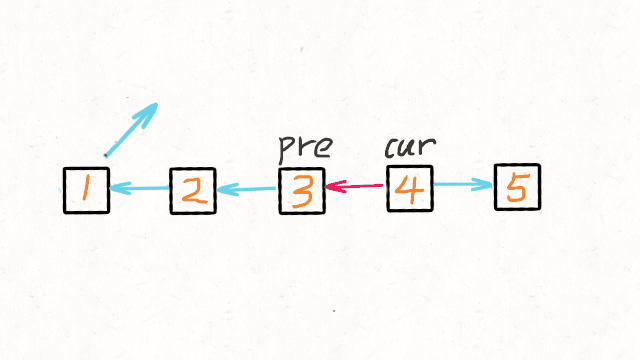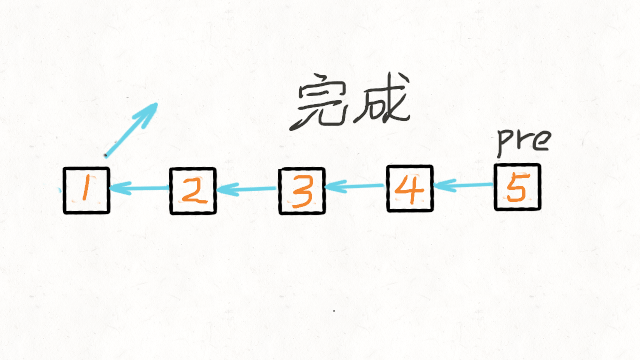
leetcodetop100 (22) 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表 简单的用一个动态数组Arraylist记录,然后倒序遍历赋值给一个新的链表,这种空间复杂度是o(n),估计需要优化。 采用双指针; 我们可以申请两个指针…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
