爬楼梯Java(斐波那契数列)
题目:有n阶楼梯,一次只能爬一层或者两层,请问有多少种方法?
这类题目其实都可以用斐波那契数列来解决,比如:
一阶楼梯只有一种方法
二阶楼梯有(1+1,2)两种方法
三阶楼梯有(1+1+1,1+2,2+1)三种方法
四阶楼梯有(1+1+1+1,1+2+1,1+1+2,2+2,2+1+1)五种方式
五阶楼梯有(1+1+1+1+1,1+1+1+2,1+2+2,1+2+1+1,1+1+2+1,2+1+1+1,2+2+1,2+1+2)八种方法,可以看出n阶楼梯是由(n-1) + (n-2)构成的,基数1阶为1,2阶为2.
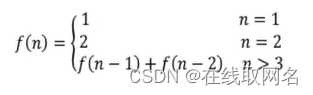
以下是代码的实现方式:
//斐波那契数列 迭代方式实现,时间复杂度低private static int calculate(int n) {if (n==1 || n==2) {return n;}int first = 1, second = 2, sum = 0;for (int i = 3; i <= n; i++) {sum = first + second;first = second;second = sum;}return sum;}//递归方式 时间复杂度高(n*2)private static int calculate1(int n) {if (n==1 || n==2) {return n;}return calculate1(n - 1) + calculate1(n - 2);}斐波那契数列结果为:89
斐波那契数列结果为:89
相关文章:
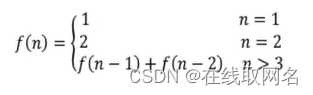
爬楼梯Java(斐波那契数列)
题目:有n阶楼梯,一次只能爬一层或者两层,请问有多少种方法? 这类题目其实都可以用斐波那契数列来解决,比如: 一阶楼梯只有一种方法 二阶楼梯有(11,2)两种方法 三阶楼梯有(111,12,21)三种方法 四阶楼梯有(1111,121,112,22,211)五种方式 五阶楼梯有(11111,1112,122,1211,1…...

Maven项目package为jar包后在window运行报A JNI error has occurred
原因:本地java版本与项目结构中使用的java版本不一致(之前因为别的需求把idea的java版本改为了18) 解决方法 打开项目结构,将idea的java版本改为与本地一致 再修改项目中的pom.xml 重新编译,package即可...
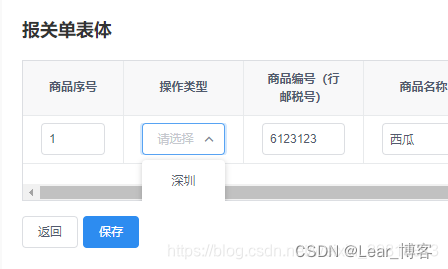
iview 的table表格组件使单元格可编辑和输入
表格的列定义中,在需要编辑的字段下使用render函数 template表格组件 <Table border :data"data" :columns"tableColumns" :loading"loading"></Table>data中定义table对象 table: {tableColumns: [{title: 商品序号,k…...

统计的基本概念及抽样分布
文章目录 🍋引言🍋总体(Population)🍋总体参数 🍋样本(Sample)🍋随机样本🍋样本统计量 🍋统计量(Statistic)🍋…...
this指针)
【C++】class的设计与使用(四)this指针
this指针 this作用域是在类内部,只能在成员函数中使用;this在成员函数的开始前构造,在成员函数的结束后清除;编译器在编译的时候也会自动加上this,它作为非静态成员函数的隐含形参,对各成员的访问均通过th…...
mysql 导入sql文件
mysql 导入sql文件 sudo mysql -uroot -p123456 -h127.0.0.1 sudo mysql -uroot -p123456 -h127.0.0.1然后 show databases;然后 use 数据库名称; 然后 source 20230920031001.sql;如果不加 -h127.0.0.1 可能会出现错误 /var/lib/mysql.sock error 通过 navicat导入的话&am…...

springcloud:三、ribbon负载均衡原理+调整策略+饥饿加载
Ribbon负载均衡原理 调整Ribbon负载均衡策略 第一种会对order-service里所有的服务消费者都采用该新规则 第二种会针对order-service里某个具体的服务消费者采用该新规则 饥饿加载...

【Unity编辑器扩展】Tranform组件自定义扩展,复制位置旋转缩放数据
目录 一、Tranform组件数据的扩展 二、 RectTransform组件数据的扩展 很多时候我们在做Tranform属性配置的时候需要反复的获取对象的位置信息,旋转信息。这个时候有个方便的工具会使得我们的效率大大提升。 一、Tranform组件数据的扩展 1.可以复制世界坐标,世界旋转 V…...

自动驾驶领域中的CMS系统应用探讨
由佐思汽研主办的“ ICVS汽车智能网联大会”正式启幕,邀请Tier1、软件供应商、操作系统商、智能驾驶及智能驾舱相关企业,共同探讨行业现状、创新技术应用交流、以及未来行业发展趋势等。 赛格导航视频产品线总监刘玉龙应邀参加本次大会,并发…...

十分钟理解OSPF路由协议
十分钟理解OSPF路由协议 1.RIP的缺陷以跳数为度量值最大跳数为15更新路由表采用全更新收敛速度慢 2.RIP与OSPF比较OSPF概述运行OSPF协议之前运行OSPF协议之后 3.OSPF协议工作过程1.发现邻居2.建立邻接关系3.传递链路状态信息4.计算路由 4.OSPF分区域管理 有RIP协议,…...

Python 编程基础 | 第一章-预备知识 | 1.4、包管理工具
一、包管理工具 1、pip简介 pip是Python自带的包管理器,它可以帮助我们安装、升级和卸载Python包。Python包是一组Python模块,它们可以提供各种功能,例如数据分析、Web开发、机器学习等等。pip可以让我们轻松地安装这些包,以便我…...
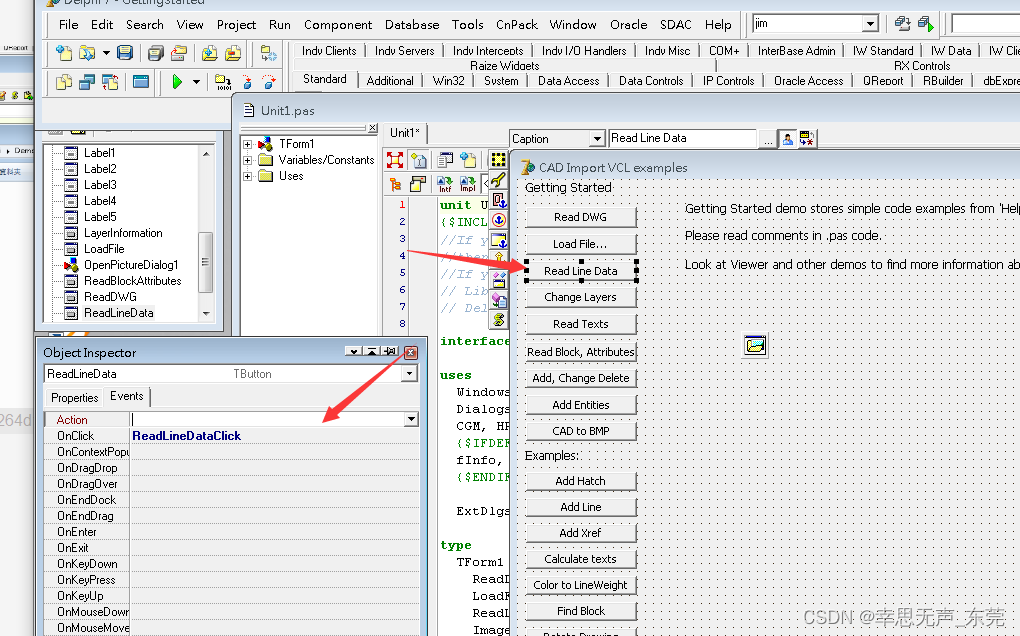
delphi中使用CADVCL 10.0 Enterprise控件解析DXF文件生成图片保存到本地
使用案例demos中GettingStarted案例 修改OnClick方法 更换代码 varvDrawing: TsgCADDXFImage;I: Integer;vEnt: TsgDXFEntity;vDXFImage:TsgCADImage;Bitmap: TBitmap;jpg: TJpegImage; beginvDrawing : TsgCADDXFImage.Create;vDrawing.LoadFromFile(d:\Entities.dxf);for …...
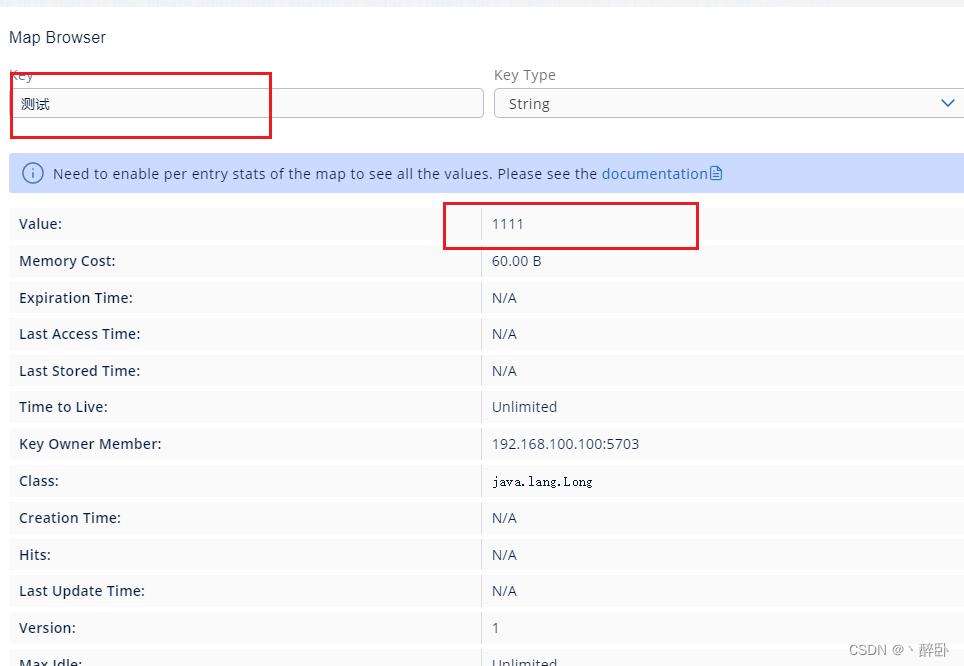
Hazelcast系列(三):hazelcast管理中心
系列文章 Hazelcast系列(一):初识hazelcast Hazelcast系列(二):hazelcast集成 Hazelcast系列(三):hazelcast管理中心 目录 前言 平台搭建 测试 其他 参考 总结 前言 前面,我们通过几种配置方式(Hazelcast系…...
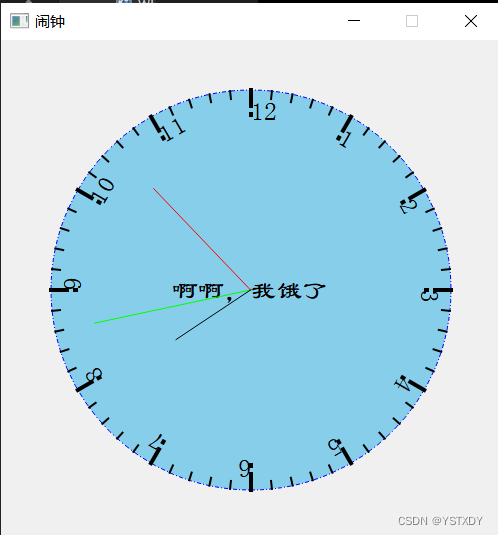
QT 绘画功能的时钟
.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPaintEvent> #include <QDebug> //信息调试类 #include <QPainter> #include <QPixmap> //图像引擎类 #include <QTime> #include <QTimer> …...
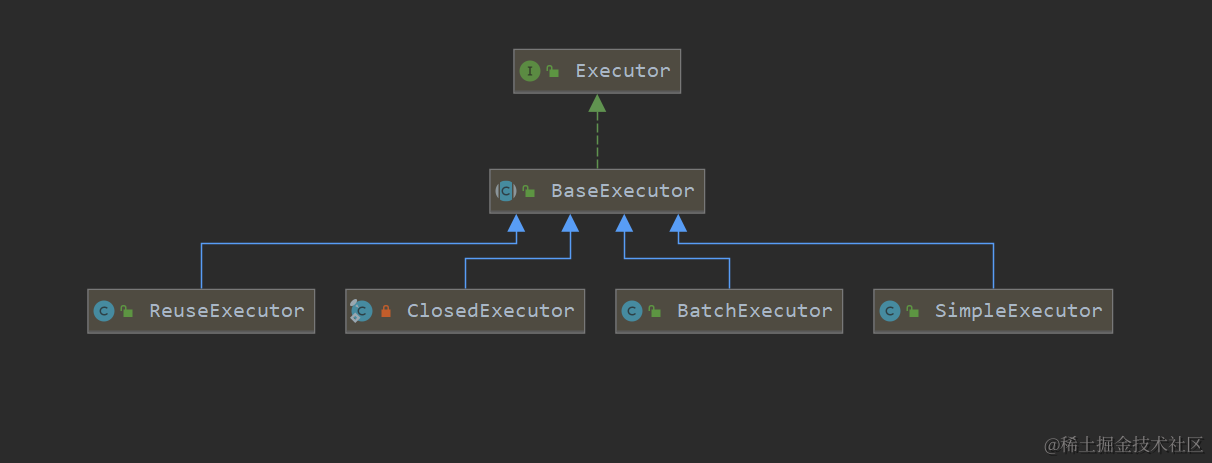
设计模式之道-模板方法模式
文章目录 模板方法模式简介作用模板方法模式的缺点模板方法模式的应用场景业务场景开源框架中的应用 对比回调和Hook模式关于组合优先于继承 关于设计模式乱用的现象 模板方法模式 简介 模板方法模式是一种行为型设计模式,该设计模式的核心在于通过抽象出一套相对…...

头哥的实践平台的Linux文件/目录管理
一 Linux 文件/目录管理 1.本关的编程任务是补全右侧代码片段中Begin至End中间的代码,具体要求如下: 新创建两个文件空文件file1和file2。 删除系统已存在的两个文件oldFile1和oldFile2。 #!/bin/bash#在以下部分写出完成任务的命令 #***********begi…...
软件测试基本常识
【软件测试面试突击班】如何逼自己一周刷完软件测试八股文教程,刷完面试就稳了,你也可以当高薪软件测试工程师(自动化测试) 一、测试用例的编写 1.在测试中最重要的文档,他是测试工作的核心,是一组在测试时…...
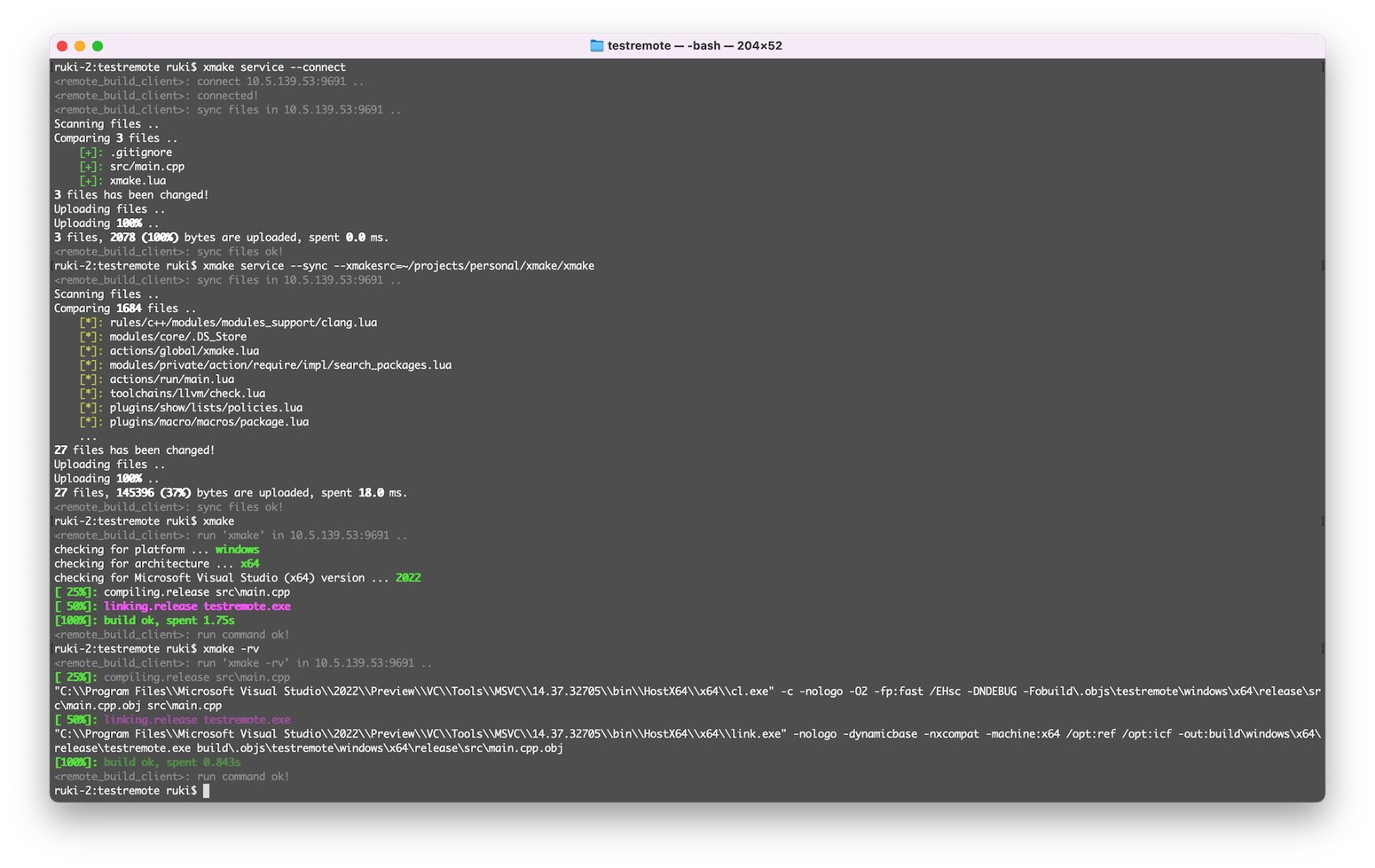
Xmake v2.8.3 发布,改进 Wasm 并支持 Xmake 源码调试
Xmake 是一个基于 Lua 的轻量级跨平台构建工具。 它非常的轻量,没有任何依赖,因为它内置了 Lua 运行时。 它使用 xmake.lua 维护项目构建,相比 makefile/CMakeLists.txt,配置语法更加简洁直观,对新手非常友好&#x…...
Serverless 数仓技术与挑战(内含 PPT 下载)
近期,Databend Labs 联合创始人张雁飞发表了题为「Serverless 数仓技术与挑战」的主题分享。以下为本次分享的精彩内容: 主题: 「Serverless 数仓技术与挑战」 演讲嘉宾: 张雁飞 嘉宾介绍: Databend Labs 联合创始人…...

九牧小牧携手国家队!一场“中国卫浴“和“中国体育”的双向奔赴
文 | 螳螂观察 作者 | 余一 1990年中国第一次举办了综合性国际体育大赛——北京亚运会,来自37个国家和地区,共计6578人的体育代表团参加了那届亚运会,一首《亚洲雄风》成为无数人记忆中的经典。 2023年杭州亚运会于近日正式拉开了帷幕&…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
