简述信息论与采样定理
信息论
香农信息论发表于1948/1949年,它由三部分组成:信号采样、信源编码、信道编码;
-
信号采样:采样理论研究在何种条件下对连续信号进行采样,从而得到的离散型号可以可逆地恢复出采样前的连续信号。采样得到的离散实数值代表着原来的信号,信号通常有限精度量化成一个有限的符号集中。
-
信源编码:信源编码研究如何将采样得到的离散数字信号编码成二进制序列,它利用了信号的统计分布来将采集到的数字信号编码成最紧凑的二进制码。
-
信道编码:信道编码研究如何给已经编码的序列中添加冗余性,从而使它对传输中引入的错误或者攻击(比如某些比特位存一定概率的翻转)更具有鲁邦性;它有时候也叫做纠错码理论。
信号采样
1.1 模拟信号与数字信号
为了能够利用数学工具分析性能,数学建模通常建立在连续信号(也称为模拟信号)上。连续信号的设定的目的是为了能够表示物理世界采集到的真实信号,比如从麦克风、数字相机或者医疗设备等传感器硬件采集的输入信号。模拟信号是一个一维函数 f 0 ∈ L 2 ( [ 0 , 1 ] ) f_0\in L^2([0,1]) f0∈L2([0,1]),其中 [ 0 , 1 ] [0,1] [0,1]表示的信号采集域,比如通常可能是时间轴。图像的模拟信号是一个二维函数 f 0 ∈ L 2 ( [ 0 , 1 ] 2 ) f_0\in L^2([0,1]^2) f0∈L2([0,1]2),其中单位正方形区域 [ 0 , 1 ] 2 [0,1]^2 [0,1]2是图像空间区域。
尽管目前仅仅关注在声音和自然图像信号的处理中,但是这些方法中绝大部分都可以延伸到多维信号数据集的处理上,多维信号具有更高的维度间的映射:
f 0 : [ 0 , 1 ] d → [ 0 , 1 ] 2 f_0:[0,1]^d\rightarrow [0,1]^2 f0:[0,1]d→[0,1]2
其中 d d d是输入空间的维度( d = 1 d=1 d=1表示声音信号, d = 2 d=2 d=2表示图像信号), s s s表示特征空间的维度。比如,对于灰度图像 d = 2 , s = 1 d=2,s=1 d=2,s=1,对于视频图像 d = 3 , s = 1 d=3,s=1 d=3,s=1,对于彩色图像 d = 2 , s = 3 d=2,s=3 d=2,s=3因为彩色图像有R/G/B三个通道。对于多光谱图像 d = 2 , s ≫ 3 d=2,s\gg 3 d=2,s≫3因为它由大量的不同波段信号的采样。图1.1和图1.2是这样信号的一些基本例子。


1.1.1 信号获取与采样
信号采集是一个通过硬件设备将连续信号采集成离散信号的低维投影映射。麦克风是一维信号采样的例子,数字相机是二维采样的例子,采样操作对应这将连续函数信号映射到N维向量N的过程,可以用如下公式表示:
f 0 ∈ L 2 ( [ 0 , 1 ] d ) → f ∈ C N f_0\in L^2([0,1]^d)\rightarrow f\in \mathbb{C}^N f0∈L2([0,1]d)→f∈CN
图1.3是一些离散信号的例子

1.1.2 线性移不变采样器
线性移不变采样器执行采样操作是将连续信号和一个不变的脉冲响应 h h h在采样位置进行卷积运算
f n = ∫ − S / 2 S / 2 f 0 ( x ) h ( n / N − x ) d x = f 0 ⋆ h ( n / N ) (1.1) f_n=\int_{-S/2}^{S/2}f_0(x)h(n/N-x)dx=f_0\star h(n/N) \tag{1.1} fn=∫−S/2S/2f0(x)h(n/N−x)dx=f0⋆h(n/N)(1.1)
函数 h ( x ) h(x) h(x)的精确形状取决于采样设备,它通常是一个低通滤波器,并且在0附近取得最大值。采样器的尺寸 S S S决定了采样设备的采样精度,它通常是与 1 / N 1/N 1/N同数量级的,如果S太大,会模糊信号,如果S太小,则会产生混叠现象。
1.2 香农采样定理
傅里叶变换回顾:对于 f ∈ L 1 ( R ) f\in L^1(\mathbb{R}) f∈L1(R),它的傅里叶变换定义为:
∀ ω ∈ R , f ^ ( ω ) = ∫ R f ( x ) e − i x ω d x . (1.2) \forall\omega\in\mathbb{R},\hat{f}(\omega)=\int_{\mathbb{R}}f(x)e^{-ix\omega}dx.\tag{1.2} ∀ω∈R,f^(ω)=∫Rf(x)e−ixωdx.(1.2)
由于有 ∣ ∣ f ^ ∣ ∣ 2 = ( 2 π ) − 1 ∣ ∣ f ∣ ∣ 2 ||\hat{f}||^2=(2\pi)^{-1}||f||^2 ∣∣f^∣∣2=(2π)−1∣∣f∣∣2,因此 f → f ^ f\rightarrow\hat{f} f→f^可以扩展到连续的 L 2 ( R ) L^2(\mathbb{R}) L2(R),这样计算函数 f f f的傅里叶变换 f ^ \hat{f} f^可以看做 l i m T → + ∞ ∫ − T T f ( x ) e − i x ω d x lim_{T\rightarrow +\infty}\int_{-T}^{T}f(x)e^{-ix\omega}dx limT→+∞∫−TTf(x)e−ixωdx。当 f ^ ∈ L 1 ( R ) \hat{f}\in L^1(\mathbb{R}) f^∈L1(R),我们可以得到傅里叶逆变换:
f ( x ) = 1 2 π ∫ R f ^ ( ω ) e i x ω d ω , (1.3) f(x)=\frac{1}{2\pi}\int_{\mathbb{R}}\hat{f}(\omega)e^{ix\omega}d\omega, \tag{1.3} f(x)=2π1∫Rf^(ω)eixωdω,(1.3)
这表示了函数 f f f是连续的,并且在 ± ∞ \pm\infty ±∞处极限趋于0。
傅里叶变换 F : f → f ^ \mathcal{F} :f\rightarrow\hat{f} F:f→f^交换了函数的正则性和衰减性。例如,如果 f ∈ C p ( R ) f\in C^p(\mathbb{R}) f∈Cp(R),具有可积的傅里叶变换,那么 F ( f ( p ) ) ( ω ) = ( i ω ) p f ^ ( ω ) \mathcal{F}(f^{(p)})(\omega)=(i\omega)^{p}\hat{f}(\omega) F(f(p))(ω)=(iω)pf^(ω),因此 ∣ f ^ ( ω ) ∣ = O ( 1 / ∣ ω ∣ p ) |\hat{f}(\omega)|=O(1/|\omega|^p) ∣f^(ω)∣=O(1/∣ω∣p)。相反地,
∫ R ( 1 + ∣ ω ∣ ) p ∣ f ^ ( ω ) ∣ d ω < + ∞ ⇒ f ∈ C p ( R ) (1.4) \int_{\mathbb{R}}(1+|\omega|)^p|\hat{f}(\omega)|d\omega<+\infty\Rightarrow f\in C^p(\mathbb{R}) \tag{1.4} ∫R(1+∣ω∣)p∣f^(ω)∣dω<+∞⇒f∈Cp(R)(1.4)
例如,当 f ^ ( ω ) = O ( 1 / ∣ ω ∣ p + 2 ) \hat{f}(\omega) =O(1/|\omega|^{p+2}) f^(ω)=O(1/∣ω∣p+2),可以推出 f ∈ C p ( R ) f\in C^p(\mathbb{R}) f∈Cp(R)。
傅里叶级数回顾:我们记 T = R / 2 π Z \mathbb{T}=\mathbb{R}/2\pi\mathbb{Z} T=R/2πZ为一系列的 2 π 2\pi 2π为周期的区间列。函数 f ∈ L 2 ( T ) f\in L^2(\mathbb{T}) f∈L2(T)是一个以 2 π 2\pi 2π为周期的函数,它可以看成 f ∈ L 2 ( [ 0 , 2 π ] ) f\in L^2([0,2\pi]) f∈L2([0,2π]),于是它的傅里叶系数为:
∀ n ∈ Z , f n ^ = 1 2 π ∫ 0 2 π f ( x ) e − i x n d x . \forall n\in\mathbb{Z},\hat{f_n}=\frac{1}{2\pi}\int_{0}^{2\pi}f(x)e^{-ixn}dx. ∀n∈Z,fn^=2π1∫02πf(x)e−ixndx.
这个公式等价于求函数 f f f与基函数 e n e_n en的内积 f n ^ = < f , e n > \hat{f_n}=<f,e_n> fn^=<f,en>,内积定义为 < f , g > = 1 2 π ∫ T f ( x ) g ‾ ( x ) d x <f,g>=\frac{1}{2\pi}\int_{\mathbb{T}}f(x)\overline{g}(x)dx <f,g>=2π1∫Tf(x)g(x)dx。在这里的内积中, e n e_n en是希尔伯特空间中的正交基,这意味着,可以通过如下收敛级数进行重建
f = ∑ n ∈ Z < f , e n > e n (1.5) f=\sum_{n\in\mathbb{Z}}<f,e_n>e_n \tag{1.5} f=n∈Z∑<f,en>en(1.5)
这意味着,在 N → + ∞ N\rightarrow +\infty N→+∞时, ∣ ∣ f − ∑ n = − N N < f , e n > e n ∣ ∣ L 2 ( T ) → 0 ||f-\sum_{n=-N}^{N}<f,e_n>e_n||_{L^2(\mathbb{T})}\rightarrow 0 ∣∣f−∑n=−NN<f,en>en∣∣L2(T)→0。如果函数 f f f可微,那么在 x ∈ T x\in\mathbb{T} x∈T上可以保证公式(1.5)按点收敛。如果函数存在阶跃点,那么在这些点数存在Gibbs震荡,从而不能保证一致收敛,但是级数仍然收敛域该点的左极限和右极限的一半。
泊松公式:泊松公式连接了傅里叶变换与傅里叶技术到信号采样与周期化操作。对于某个定义在 R \mathbb{R} R的函数 h ( ω ) h(\omega) h(ω),它的周期化为:
h P ( ω ) = ∑ n h ( ω − 2 π n ) (1.6) h_P(\omega)=\sum_{n}h(\omega-2\pi n) \tag{1.6} hP(ω)=n∑h(ω−2πn)(1.6)
这个公式有意义的前提是 h ∈ L 1 ( R ) h\in L^1(\mathbb{R}) h∈L1(R), 并且在这种情况下 ∣ ∣ h P ∣ ∣ L 1 ( T ) ≤ ∣ ∣ h ∣ ∣ L 1 ( R ) ||h_P||_{L^1(\mathbb{T})}\le ||h||_{L^1(\mathbb{R})} ∣∣hP∣∣L1(T)≤∣∣h∣∣L1(R)。泊松公式阐明了如下关系:
(1)信号 f ( x ) f(x) f(x)通过采样得到采样序列 ( f ( n ) ) n (f(n))_n (f(n))n,对采样采样序列的傅里叶级数为 ∑ n f ( n ) e − i ω n \sum_{n}f(n)e^{-i\omega n} ∑nf(n)e−iωn;
(2)信号 f ( x ) f(x) f(x)做傅里叶变换得到 f ^ ( ω ) \hat{f}(\omega) f^(ω),对傅里叶此福利也变化进行周期化,得到傅里叶级数 ∑ n f ( n ) e − i ω n \sum_{n}f(n)e^{-i\omega n} ∑nf(n)e−iωn;
引理1 (泊松公式):假设 f ^ \hat{f} f^是紧支撑的,并且 ∣ f ( x ) ∣ ≤ C ( 1 + ∣ x ∣ ) − 3 |f(x)|\le C(1+|x|)^{-3} ∣f(x)∣≤C(1+∣x∣)−3,其中C为某个常数,于是有
∀ ω ∈ R , ∑ n f ( n ) e − i ω n = f ^ P ( ω ) . (1.7) \forall\omega\in\mathbb{R}, \sum_{n}f(n)e^{-i\omega n}=\hat{f}_P(\omega). \tag{1.7} ∀ω∈R,n∑f(n)e−iωn=f^P(ω).(1.7)
证明:由于 f ^ \hat{f} f^是紧支撑的, f ^ P \hat{f}_P f^P是良定义的,并且 f f f很快衰减,由公式(1.4)可知 ( f ^ ) P (\hat{f})_P (f^)P是 C 1 C^1 C1。于是可以由傅里叶级数展开
( f ^ ) P ( ω ) = ∑ k c k e i k ω (1.8) (\hat{f})_P(\omega)=\sum_{k}c_ke^{ik\omega} \tag{1.8} (f^)P(ω)=k∑ckeikω(1.8)
其中
c k = 1 2 π ∫ 0 2 π ( f ^ ) P ( ω ) e − i k ω d ω = 1 2 π ∫ 0 2 π ∑ n f ^ ( ω − 2 π n ) e − i k ω d ω c_k=\frac{1}{2\pi}\int_{0}^{2\pi}(\hat{f})_P(\omega)e^{-ik\omega}d\omega=\frac{1}{2\pi}\int_{0}^{2\pi}\sum_{n}\hat{f}(\omega-2\pi n)e^{-ik\omega}d\omega ck=2π1∫02π(f^)P(ω)e−ikωdω=2π1∫02πn∑f^(ω−2πn)e−ikωdω
又有
∫ 0 2 π ∑ n ∣ f ^ ( ω − i π n ) e − i k ω ∣ d ω = ∫ R ∣ f ^ ∣ \int_{0}^{2\pi}\sum_{n}|\hat{f}(\omega-i\pi n)e^{-ik\omega}|d\omega = \int_{\mathbb{R}}|\hat{f}| ∫02πn∑∣f^(ω−iπn)e−ikω∣dω=∫R∣f^∣
由于 f ^ ∈ L 1 ( R ) \hat{f}\in L^{1}(\mathbb{R}) f^∈L1(R)是有界的,因此可以交换求和符号与积分号的运算顺序
c k = ∑ n 1 2 π ∫ 0 2 π f ^ ( ω − 2 π n ) e − i k ω d ω = 1 2 π ∫ m a t h b b R f ^ ( ω ) e − i k ω d ω = f ( − k ) c_k=\sum_{n}\frac{1}{2\pi}\int_{0}^{2\pi}\hat{f}(\omega-2\pi n)e^{-ik\omega}d\omega=\frac{1}{2\pi}\int_{mathbb{R}}\hat{f}(\omega)e^{-ik\omega}d\omega=f(-k) ck=n∑2π1∫02πf^(ω−2πn)e−ikωdω=2π1∫mathbbRf^(ω)e−ikωdω=f(−k)
由于 f ^ ∈ L 1 ( R ) \hat{f}\in L^1(\mathbb{R}) f^∈L1(R),因此这里我们运用(1.3)式中的傅里叶反变换是合理的。
注:这里我们进一步解释一下引理1的内容,信号 f ( t ) f(t) f(t)的傅里叶变换为 f ^ ( ω ) \hat{f}(\omega) f^(ω),我们对信号 f ( t ) f(t) f(t)在离散点 n n n处进行采样得到离散信号 f ( n ) f(n) f(n),离散信号 f ( n ) f(n) f(n)的福利变换为 ∑ n f ( n ) e − i ω n \sum_{n}f(n)e^{-i\omega n} ∑nf(n)e−iωn,而引理1则说明了离散采样信号 f ( n ) f(n) f(n)的傅里叶变换等于原始连续信号 f ( t ) f(t) f(t)的傅里叶变换按照以 2 π 2\pi 2π为周期进行周期化的结果。
香农采样定理:香农采样定理描述在什么采样步长 s > 0 s>0 s>0的采样操作 f → ( f ( n s ) ) n f\rightarrow (f(ns))_n f→(f(ns))n下信号可以可逆恢复出原始信号的充分条件。它需要采样信号的频谱满足 s u p p ( f ^ ) ⊂ [ − π / s , π / s ] supp(\hat{f})\subset [-\pi/s,\pi/s] supp(f^)⊂[−π/s,π/s]。这个定理被奈奎斯特在1928年重新证明。它由于香农将其放于数字通信的论文中而变得非常出名。

定理1:如果对于某个常数C有 ∣ f ( x ) ∣ ≤ C ( 1 + ∣ x ∣ ) − 3 |f(x)|\le C(1+|x|)^{-3} ∣f(x)∣≤C(1+∣x∣)−3且 s u p p f ^ ⊂ [ − π / s , π / s ] supp\hat{f}\subset [-\pi/s,\pi/s] suppf^⊂[−π/s,π/s],于是有
∀ x ∈ R f ( x ) = ∑ n f ( n s ) s i n c ( x / s − n ) ,其中 s i n c ( u ) = s i n ( π u ) π u (1.9) \forall x\in\mathbb{R}f(x)=\sum_{n}f(ns)sinc(x/s-n),其中sinc(u)=\frac{sin(\pi u)}{\pi u} \tag{1.9} ∀x∈Rf(x)=n∑f(ns)sinc(x/s−n),其中sinc(u)=πusin(πu)(1.9)
一致收敛。
证明:令 g ( x ) = f ( s x ) g(x)=f(sx) g(x)=f(sx),那么 g ^ ( ω ) = 1 / s f ^ ( ω / s ) \hat{g}(\omega)=1/s\hat{f}(\omega/s) g^(ω)=1/sf^(ω/s),事实上,令 z = s x z=sx z=sx,那么有
g ^ ( ω ) = ∫ f ( s x ) e − i ω x d x = 1 s ∫ f ( z ) e − i ( ω / s ) z d z = f ^ ( ω / s ) / s , \hat{g}(\omega)=\int f(sx)e^{-i\omega x}dx=\frac{1}{s}\int f(z)e^{-i(\omega/s)z}dz=\hat{f}(\omega/s)/s, g^(ω)=∫f(sx)e−iωxdx=s1∫f(z)e−i(ω/s)zdz=f^(ω/s)/s,
为了研究方便,我们把 s s s置为1。紧支撑假设含有 f ^ ( ω ) = 1 [ − p i , p i ] ( ω ) f ^ P ( ω ) \hat{f}(\omega)=1_{[-pi,pi]}(\omega)\hat{f}_P(\omega) f^(ω)=1[−pi,pi](ω)f^P(ω)。联合(1.3)式的逆变换与泊松公式(1.8),有
f ( x ) = 1 2 π ∫ − ∞ + ∞ f ^ ( ω ) e i ω x d ω = 1 2 π ∫ π π f ^ P ( ω ) e i ω x = 1 2 π ∫ − π π ∑ n f ( n ) e i ω ( x − n ) d ω . f(x)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\hat{f}(\omega)e^{i\omega x}d\omega=\frac{1}{2\pi}\int_{\pi}^{\pi}\hat{f}_P(\omega)e^{i\omega x}=\frac{1}{2\pi}\int_{-\pi}^{\pi}\sum_nf(n)e^{i\omega (x-n)}d\omega. f(x)=2π1∫−∞+∞f^(ω)eiωxdω=2π1∫ππf^P(ω)eiωx=2π1∫−ππn∑f(n)eiω(x−n)dω.

由于 f f f很快衰减,于是 ∫ − π π ∑ n ∣ f ( n ) e i ω ( x − n ) ∣ d ω = ∑ n ∣ f ( n ) ∣ < + ∞ \int_{-\pi}^{\pi}\sum_{n}|f(n)e^{i\omega(x-n)}|d\omega=\sum_n|f(n)|<+\infty ∫−ππ∑n∣f(n)eiω(x−n)∣dω=∑n∣f(n)∣<+∞,因此可以交换求和与积分运算顺序,于是有
f ( x ) = ∑ n f ( n ) 1 2 π ∫ − π π e i ω ( x − n ) d ω = ∑ n f ( x ) s i n c ( x − n ) f(x)=\sum_{n}f(n)\frac{1}{2\pi}\int_{-\pi}^{\pi}e^{i\omega (x-n)}d\omega=\sum_{n}f(x)sinc(x-n) f(x)=n∑f(n)2π1∫−ππeiω(x−n)dω=n∑f(x)sinc(x−n)
对于 s s s取其他值,上面的证明过程类似。
定理1的重构公式存在一个问题,它用了一个衰减缓慢且震荡剧烈的 s i n c ( x ) sinc(x) sinc(x)核函数。在实际应用中,我们很少用这样的核函数的来插值,而是更新换选择更光滑且局部性能更好的核函数。如果 s u p p ( f ^ ) ⊂ [ − π / s ′ , π / s ′ ] supp(\hat{f})\subset [-\pi/s^{'},\pi/s^{'}] supp(f^)⊂[−π/s′,π/s′],其中 s ′ > s s^{'}>s s′>s(也就是,具有更窄的频带),我们也可以重新证明这个采样与重构过程,于是可以具有更多的自由度来设计重构核函数,现在可以选则在频域更窄,在时域指数衰减的核函数。
样条插值函数的定义为: ϕ 0 = 1 [ − 1 / 2 , 1 / 2 ] \phi_0=1_{[-1/2,1/2]} ϕ0=1[−1/2,1/2],且 ϕ k = ϕ k − 1 ∗ ϕ 0 \phi_k=\phi_{k-1}*\phi_0 ϕk=ϕk−1∗ϕ0,它是一个分线多项式函数,阶数为 k k k,并且有 k k k阶有界导数,在区间 [ − ( k + 1 ) / 2 , ( k + 1 ) / 2 ] [-(k+1)/2,(k+1)/2] [−(k+1)/2,(k+1)/2]上紧支撑。采用样条函数作为插值核函数的重构公式为 f ( x ) ≈ f ~ ( x ) = ∑ n a n ϕ ( x − n ) f(x)\approx\tilde{f}(x)=\sum_{n}a_n\phi(x-n) f(x)≈f~(x)=∑nanϕ(x−n),其中 ( a n ) n (a_n)_n (an)n通过 ( f ( n ) ) n (f(n))_n (f(n))n求解线性系统求得。仅在 k ∈ 0 , 1 k\in {0,1} k∈0,1时有 a n = f ( n ) a_n = f(n) an=f(n)。在实际经常用的是三次样条插值,对应的 k = 3 k=3 k=3。

这个理论也解释了在信号 f f f的傅里叶变换 f ^ \hat{f} f^的支撑区间不是 [ − π / s , p i / s ] [-\pi/s,pi/s] [−π/s,pi/s]时会发生什么。这是会发生信号混叠现象,在支撑区间 [ − π / s , p i / s ] [-\pi/s,pi/s] [−π/s,pi/s]的高频信号引起低频信号的的混乱叠加,通常称为混叠现象。如果输入信号不是带宽有限的,那么在采样之前进行一个预滤波(平滑),过滤掉频率支撑区间 [ − π / s , p i / s ] [-\pi/s,pi/s] [−π/s,pi/s]之外的高频信号非常重要,这样可以有效的避免混叠现象。

量化:在已经采集得到信号的离散序列之后,为了能够有效存储和传输,需要把信号用有限精度去量化。后面的信号压缩章节会详细降到如何通过变换编码在变换域中进行高效编码与量化,这对于增强信源编码的性能非常有用。然而,常用的量化策略是直接在采样信号上进行量化操作。

例如,在采样步长为 s = 1 / N s=1/N s=1/N时,采集到长度问N的信号向量 ( u n = f ( n / N ) ) n = 1 N ∈ R N (u_n=f(n/N))_{n=1}^{N}\in \mathbb{R}^N (un=f(n/N))n=1N∈RN,由于函数 f f f在有限的空间区间与香农采样定理需要函数的傅里叶变换 f ^ \hat{f} f^也是带宽有限互相矛盾,因为一个函数 f f f不可能同时在时间域与频率域同时具有紧支撑特性,因此在有限的存储空间上完美重构信号是不可能的。
选择一个量化步长 T T T,量化算子 v n = Q T ( u n ) ∈ Z v_n=Q_T(u_n)\in\mathbb{Z} vn=QT(un)∈Z在距离 T T T的整数倍附近取整,例如
v = Q t ( u ) ⇔ v − 1 2 ≤ u / T < v + 1 2 , v=Q_t(u)\Leftrightarrow v-\frac{1}{2}\le u/T \lt v+\frac{1}{2}, v=Qt(u)⇔v−21≤u/T<v+21,
如图1.8所示。恢复信号的过程需要去量化,最好的重构是 D T ( v ) = T v D_T(v)=Tv DT(v)=Tv。量化然后取量化过程引入的最大误差是 T / 2 T/2 T/2,因为 ∣ D T ( Q T ( u ) ) − u ∣ ≤ T / 2 |D_T(Q_T(u))-u|\le T/2 ∣DT(QT(u))−u∣≤T/2。量化过程是香农标准过程中唯一的误差引入源。

信号与图像的编码理论后续会单独开一个章节详细讲述,这里暂时略过。
信道编码及纠错码理论是数字通信领域的核心内容,数字通信不是我们研究的重点,后续章节变不会继续论述。
注:未经授权,严谨转载!!!
如有错误或者不解,欢迎批评指正,欢迎私信笔者讨论。
相关文章:

简述信息论与采样定理
信息论 香农信息论发表于1948/1949年,它由三部分组成:信号采样、信源编码、信道编码; 信号采样:采样理论研究在何种条件下对连续信号进行采样,从而得到的离散型号可以可逆地恢复出采样前的连续信号。采样得到的离散实…...

网络安全之网站常见的攻击方式
这是作者自学的哈,不算课程内容。 网页中出现大量黑链 网站看着很正常,但是会隐藏一些链接。网页的链接几乎都是标签,这种黑链就是通过链接标签<a></a>或者script在里面链入恶意脚本,等待浏览者的访问,通…...
)
iOS Swift 拍照识别数字(Recognizing Text in Images)
可以用腾讯云 OCR的iOS demo - 腾讯云 苹果官方的解决方案(识别度太低) Recognizing Text in Images - apple developer Extracting phone numbers from text in images(Sample Code) - apple developer import UIKit import Visionclass ViewContro…...

数学建模:智能优化算法及其python实现
数学建模:智能优化算法及其python实现 智能优化算法简介差分进化算法(Differential Evolution,DE)遗传算法(Genetic Algorithm,GA)粒子群优化算法(Particle Swarm Optimization,PSO)模拟退火算法(Simulated Annealing,SA)蚁群算法(Ant Colony Optimization,ACO)…...
monkeyrunner环境搭建和初步用法
一、打开模拟器 运行monkeyrunner之前必须先运行相应的模拟器,不然monkeyrunner无法连接设备。 用Elipse打开Android模拟器或在CMD中用Android命令打开模拟器。这里重点讲一下在CMD中用Android命令打开模拟器 命令:emulator -avd test (注…...
)
2024华为校招面试真题汇总及其解答(一)
1. 我问你点java基础的问题吧,你平时都用什么集合啊,都什么情况下使用 在 Java 中,常用的集合有以下几种: List:有序集合,可以重复,常用实现类有 ArrayList、LinkedList、Vector。Set:无序集合,不能重复,常用实现类有 HashSet、TreeSet。Map:键值对集合,键不能重复…...

css调整字体间距 以及让倾斜字体
调整字体间距 .element {letter-spacing: 2px; /* 调整为适当的值 */ }倾斜字体1 .element {font-style: italic; }请注意,不是所有的字体都有斜体样式可用。如果字体本身没有斜体版本,则可能无法实现完全的斜体效果。 倾斜字体2 <span class"…...
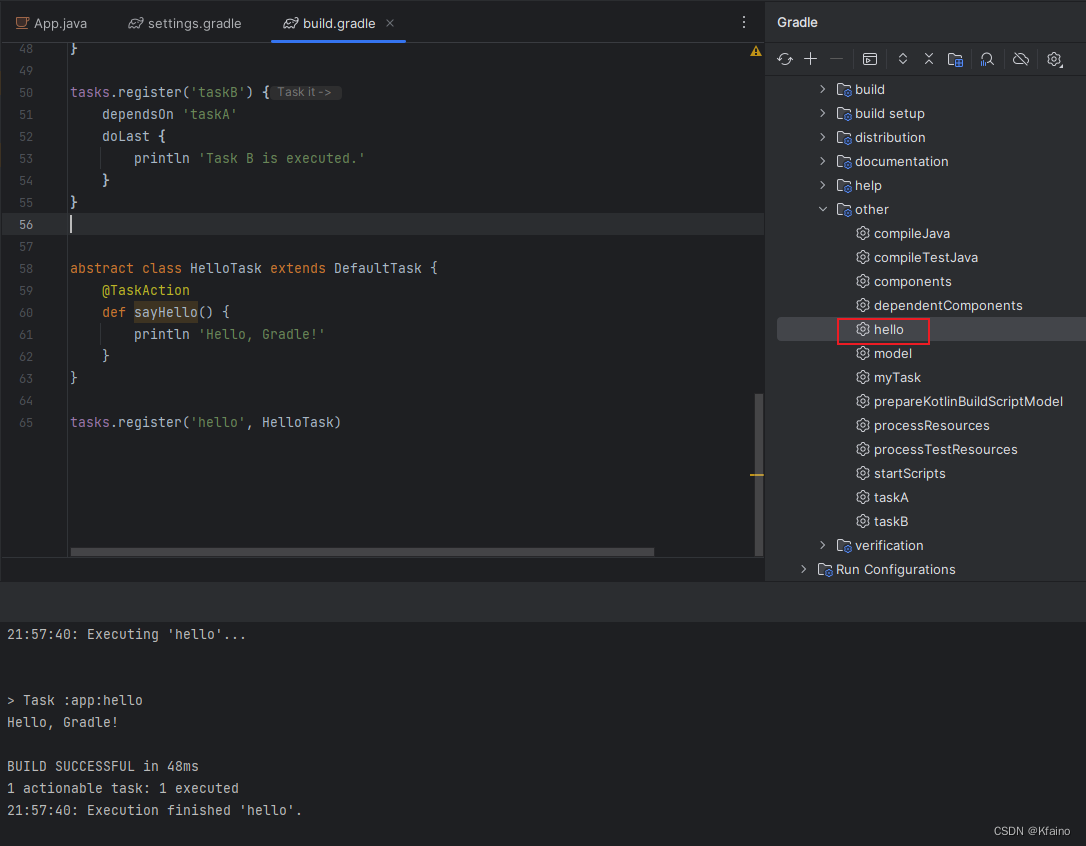
工具篇 | Gradle入门与使用指南 - 附Github仓库地址
介绍 1.1 什么是Gradle? Gradle是一个开源构建自动化工具,专为大型项目设计。它基于DSL(领域特定语言)编写,该语言是用Groovy编写的,使得构建脚本更加简洁和强大。Gradle不仅可以构建Java应用程序&#x…...

使用 Python 函数callable和isinstance的意义
一、说明 在这篇博客中,我们将探讨两个python函数:1 callable 中的函数及其有趣的应用程序。该callable函数用于检查对象是否可调用,这意味着它可以作为函数调用。2 isinstance这个内置函数允许我们比较两种不同的数据类型并确定它们是否相…...
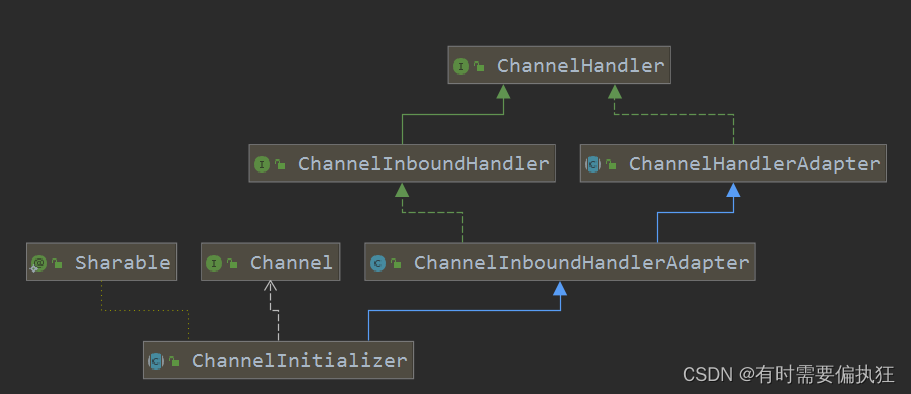
Netty场景及其原理
Netty场景及其原理 Netty简化Java NIO的类库的使用,包括Selector、 ServerSocketChannel、 SocketChannel、ByteBuffer,解决了断线重连、 网络闪断、心跳处理、半包读写、 网络拥塞和异常流的处理等。Netty拥有高性能、 吞吐量更高,延迟更低…...

Java接口和接口继承
Java接口和接口继承 接口 在抽象类中,抽象方法本质上是定义接口规范,即规定高层类的接口,从而保证所有子类都有相同的接口实现,这样,多态就能发挥出威力。 如果一个抽象类没有字段,所有方法全部都是抽象方…...
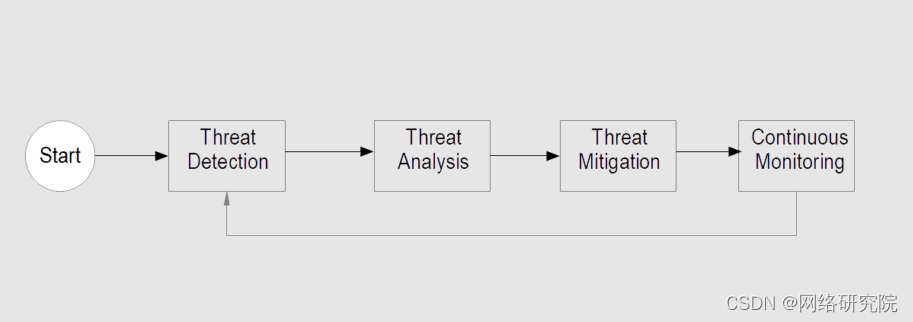
2023 年解锁网络安全即服务
在当今快速发展的数字世界中,强大的网络安全机制的重要性怎么强调都不为过。对于越来越多地发现自己成为网络威胁焦点的小型企业来说尤其如此。 那么,“网络安全即服务”到底是什么?为什么它对小型企业至关重要? 网络安全即服务…...
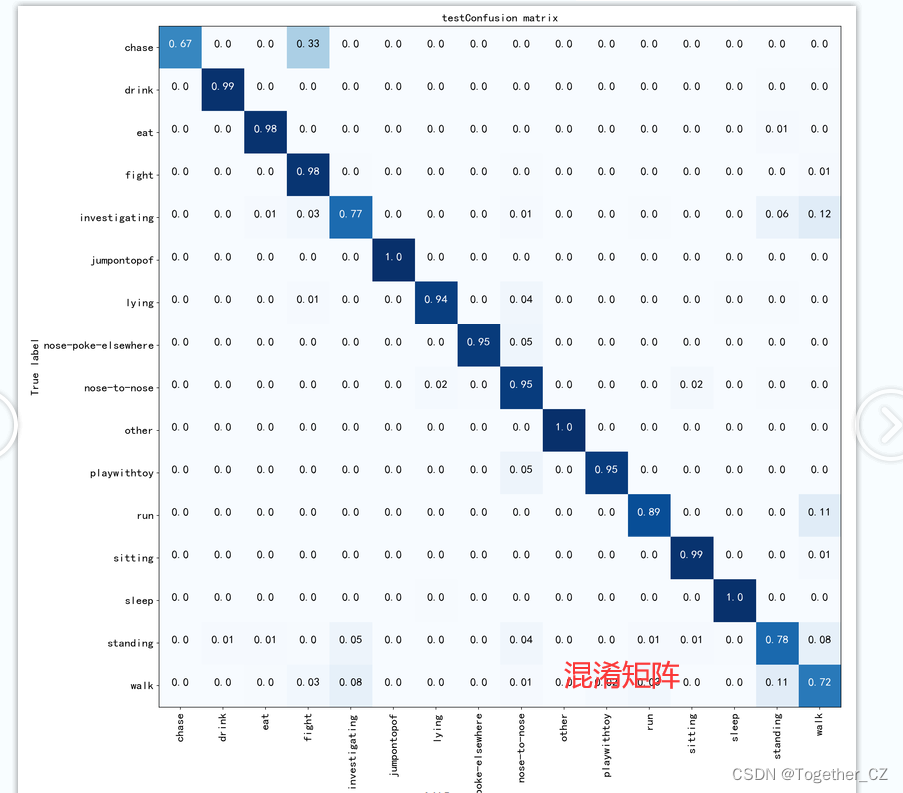
python基于轻量级卷积神经网络模型GhostNet开发构建养殖场景下生猪行为识别系统
养殖业的数字化和智能化是一个综合应用了互联网、物联网、人工智能、大数据、云计算、区块链等数字技术的过程,旨在提高养殖效率、提升产品质量以及促进产业升级。在这个过程中,养殖生猪的数字化智能化可以识别并管理猪的行为。通过数字化智能化系统&…...

Selenium自动化测试 —— 通过cookie绕过验证码的操作!
验证码的处理 对于web应用,很多地方比如登录、发帖都需要输入验证码,类型也多种多样;登录/核心操作过程中,系统会产生随机的验证码图片,进行验证才能进行后续操作 解决验证码的方法如下: 1、开发做个万能…...
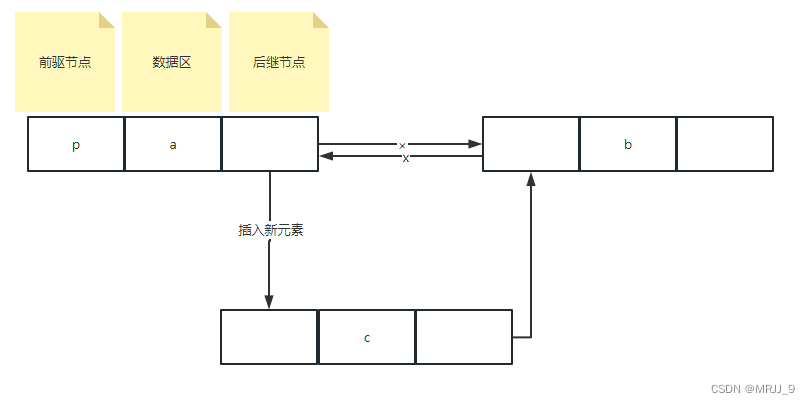
链表(单链表、双链表)
前言:链表是算法中比较难理解的部分,本博客记录单链表、双链表学习,理解节点和指针的使用,主要内容包括:使用python创建链表、实现链表常见的操作。 目录 单链表 双链表 单链表 引入链表的背景: 先来看…...

面试题08.05.递归算法
递归乘法。 写一个递归函数,不使用 * 运算符, 实现两个正整数的相乘。可以使用加号、减号、位移,但要吝啬一些。 示例1: 输入:A 1, B 10输出:10示例2: 输入:A 3, B 4输出:12提示: 保证乘法…...

分布式IT监控系统
公司的IT系统越来越复杂,对运维和维护服务的需求也越来越高。在这种环境下,分布式IT监控系统应运而生。它逐渐成为公司提高运营效率、保证业务高效运营的关键工具,功能强大,性能优良。 分布式IT监控系统是什么? 分布…...

Redis 是什么?
Redis是一种基于内存的数据库,数据的读写都是在内存中完成的,因此读写速度非常的快,常用于缓存,消息队列,分布式锁等场景。 Redis 在高并发项目中,担任着非常重要的作用,扛高并发的,…...

本地源制作
title: 本地源制作 createTime: 2020-10-29 18:05:52 updateTime: 2020-10-29 18:05:52 categories: linuxyum tags: 制作本地源 通过 createrepo 制作本地源 前提 : 前提制作本地源的机器可以安装 这个软件例如 下载nginx的时候 自己加上 nginx的yum的数据源 (rp…...

树莓派(Linux系统通用)交叉编译(环境搭建、简单使用)
概念 交叉编译是指在一台计算机上编译运行在另一台计算机上的程序。(编译是指,在一个平台上生成在该平台上的可执行程序)通常情况下,编译器和目标平台的架构是不同的,例如,在一台x86平台上编译运行在ARM平…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...
