【数值计算方法】非线性方程(组)和最优化问题的计算方法:非线性方程式求根的二分法、迭代法、Newton 迭代法及其Python实现
目录
一、非线性方程式求根
1、二分法(Bisection Method、对分法)
a. 理论简介
b. python实现
2、迭代法(Iterative Method)
a. 理论简介
b. python实现
3、Newton 迭代法(Newton's Method)
a. 理论简介
b. python实现
一、非线性方程式求根
非线性方程举例:
非线性方程式求根是一个重要的数值计算问题,常用的方法包括二分法、迭代法和牛顿迭代法。
1、二分法(Bisection Method、对分法)
a. 理论简介
(连续函数介值定理)
二分法是一种简单而直观的求根方法,适用于单调函数的根。它的基本思想是通过不断缩小根所在区间来逼近根的位置。具体步骤如下:
- 首先,选择一个初始区间[a, b],确保函数在这个区间内连续且函数值异号(即f(a) * f(b) < 0)。
- 然后,计算区间的中点c = (a + b) / 2,并计算函数在c处的值f(c)。
- 接下来,根据f(c)与0的关系,确定新的区间[a, c]或[c, b],使得新的区间内仍满足函数值异号的条件。
- 重复上述步骤,直到满足预设的精度要求,即根的近似值落在所选区间内。
b. python实现
def f(x):return 5 * x**4 + 3 * x + 1def bisection_method(a, b, tolerance=1e-6, max_iterations=100):if f(a) * f(b) >= 0:return Nonefor _ in range(max_iterations):c = (a + b) / 2if abs(f(c)) < tolerance:return cif f(c) * f(a) < 0:b = celse:a = creturn None# 调用二分法求解方程的根
root = bisection_method(a=-1, b=0)
if root is not None:print("方程的一个根为:", root)
else:print("未找到方程的根")注意,二分法要求初始区间[a, b]满足f(a) * f(b) < 0,即方程在区间的两个端点上取值异号。
输出:
a=-0.5, b=1
方程的一个根为: -0.36193275451660156a=-1, b=0
未找到方程的根2、迭代法(Iterative Method)
a. 理论简介
迭代法是一种通过不断迭代逼近根的方法,适用于任意函数的根。它的基本思想是从一个初始的近似值开始,通过不断更新逼近根的位置,直到满足预设的精度要求。具体步骤如下:
- 首先,选择一个初始的近似值x0。
- 然后,根据迭代公式x[i+1] = g(x[i]),计算下一个近似值x[i+1]。
- 重复上述步骤,直到满足预设的精度要求,即近似值与根的差值足够小。
b. python实现
def g(x):return (-1) / (5 * x**3 + 3)def iterative_method(initial_guess, tolerance=1e-6, max_iterations=100):x = initial_guessfor _ in range(max_iterations):x_next = g(x)if abs(x_next - x) < tolerance:return x_nextx = x_nextreturn None# 调用迭代法求解方程的根
root = iterative_method(initial_guess=0)
if root is not None:print("方程的一个根为:", root)
else:print("未找到方程的根")注意,迭代法的收敛性与迭代函数的选择密切相关,对于某些函数可能无法收敛或者收敛速度很慢。
输出:
方程的一个根为: -0.361932924386728973、Newton 迭代法(Newton's Method)
a. 理论简介
牛顿迭代法是一种快速收敛的求根方法,适用于光滑函数的根。它利用函数的局部线性近似来逼近根的位置。具体步骤如下:
- 首先,选择一个初始的近似值x0。
- 然后,根据牛顿迭代公式x[i+1] = x[i] - f(x[i]) / f'(x[i]),计算下一个近似值x[i+1]。
- 重复上述步骤,直到满足预设的精度要求,即近似值与根的差值足够小。
b. python实现
def f(x):return 5 * x**4 + 3 * x + 1def f_prime(x):return 20 * x**3 + 3def newton_method(initial_guess, tolerance=1e-6, max_iterations=100):x = initial_guessfor _ in range(max_iterations):delta_x = f(x) / f_prime(x)x -= delta_xif abs(delta_x) < tolerance:return xreturn None# 调用牛顿迭代法求解方程的根
root = newton_method(initial_guess=0)
if root is not None:print("方程的一个根为:", root)print(int(f(root)))
else:print("未找到方程的根")
注意,牛顿法要求2阶导不编号,1阶导不为0
输出:
方程的一个根为: -0.3619330489831212
相关文章:

【数值计算方法】非线性方程(组)和最优化问题的计算方法:非线性方程式求根的二分法、迭代法、Newton 迭代法及其Python实现
目录 一、非线性方程式求根 1、二分法(Bisection Method、对分法) a. 理论简介 b. python实现 2、迭代法(Iterative Method) a. 理论简介 b. python实现 3、Newton 迭代法(Newtons Method) a. 理论…...

linux主机名
title: linux主机名 createTime: 2020-10-29 18:05:52 updateTime: 2020-10-29 18:05:52 categories: linux tags: Linux系统的主机名 查询主机名 hostnamehostnamectl 修改主机名 hostnamectl set-hostname <newhostname>...

前端uniapp图片select联动文本切换
图片 代码 <template><!-- 这个是uniapp的下拉框 --><uni-data-select v-model"pay_type" :localdata"range" change"handleSelectChange"></uni-data-select><!-- 图片 --><image :src"dynamicImage&qu…...

java - 包装类
目录 前言 一 什么是包装类? 1.获取包装类的两种方式(了解)(已经淘汰) 2.两种方式获取对象的区别(掌握) 3.自动装箱&&自动装箱 4.Integer常用方法 总结 前言 大家好,今天给大家讲解一下包装类 一 什么是包装类? 在Java中,每个基本数据类型都有对应…...

防火墙基础
目录 1、 防火墙支持那些NAT技术,主要应用场景是什么? 2、当内网PC通过公网域名解析访问内网服务器时,会存在什么问题,如何解决? 3、防火墙使用VRRP实现双机热备时会遇到什么问题,如何解决? 4…...
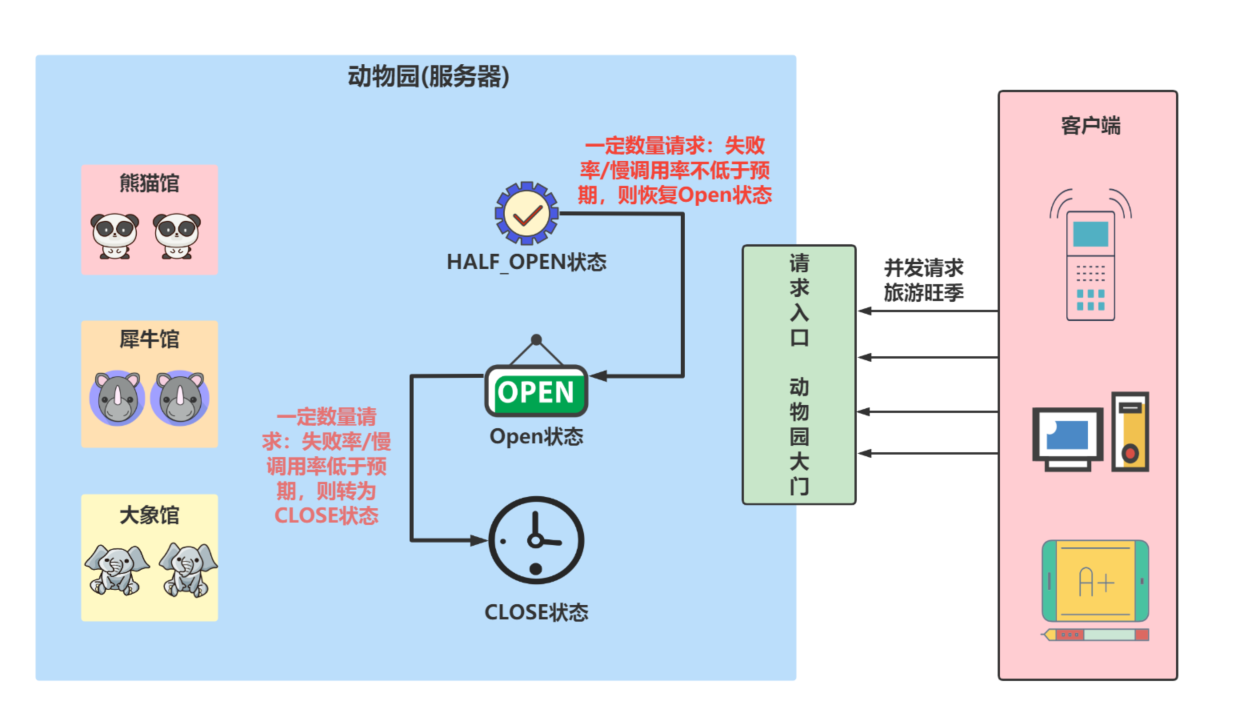
服务断路器_Resilience4j的断路器
断路器(CircuitBreaker)相对于前面几个熔断机制更复杂,CircuitBreaker通常存在三种状态(CLOSE、OPEN、HALF_OPEN),并通过一个时间或数量窗口来记录当前的请求成功率或慢速率,从而根据这些指标来…...

微信小程序学习笔记3.0
第3章 资讯类:仿今日头条微信小程序 3.1 需求描述及交互分析 需求描述 仿今日头条微信小程序,要具有以下功能。 (1)首页新闻频道框架设计,包括底部标签导航设计、新闻检索框设计及新闻频道滑动效果设计。 (2)首页新闻内容设计,包括新闻标题、新闻图片及新闻评论设计…...
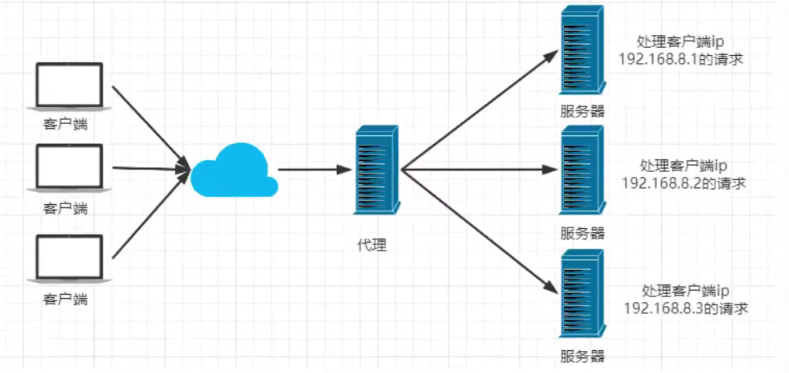
nginx 反向代理 负载均衡 动静分离
一样东西的诞生通常都是为了解决某些问题,对于 Nginx 而言,也是如此。 比如,你出于无聊写了一个小网站,部署到 tomcat 之后可以正常访问 但是后来,你的这个小网站因为内容很诱人逐步的火了,用户越来越多&a…...
后端二次开发环境搭建)
Codeanalysis(tca)后端二次开发环境搭建
先试用官方脚本文件件quick_install.sh将整个项目启动起来,然后到每个微服务下查看每个服务的pid进程,需要调试哪个先把对应的微服务关闭手动启动,具体启动流程如下: cd 到项目根目录下 source script\config.sh # 激活系统环境…...
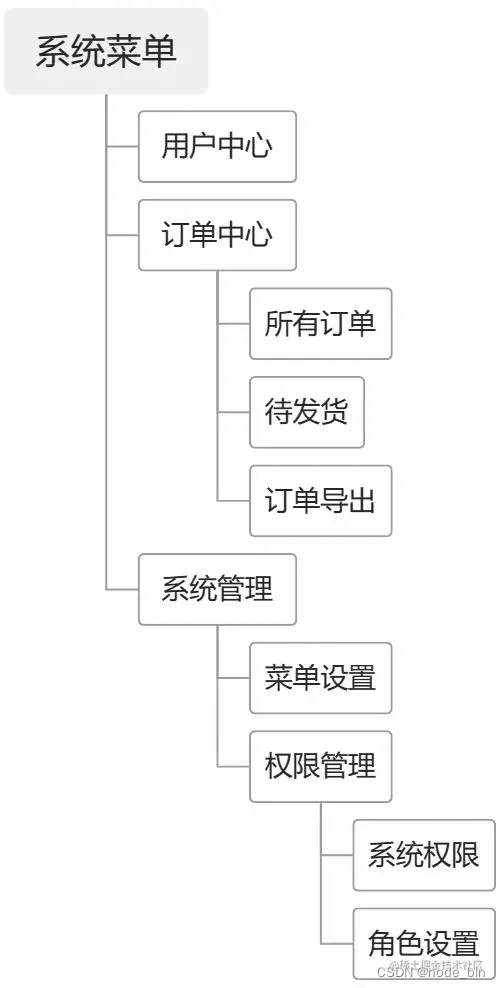
JS前端树形Tree数据结构使用
前端开发中会经常用到树形结构数据,如多级菜单、商品的多级分类等。数据库的设计和存储都是扁平结构,就会用到各种Tree树结构的转换操作,本文就尝试全面总结一下。 如下示例数据,关键字段id为唯一标识,pid为父级id&am…...

Automation Anywhere推出新的生成式AI自动化平台,加速提高企业生产力
在9 月 19 日的Imagine 2023 大会上,智能自动化领域的领导者 Automation Anywhere 宣布对其自动化平台进行扩展。推出了新的 Responsible AI Layer,并宣布了四项关键产品更新,包括全新的 Autopilot,它可以利用生成式 AI ÿ…...
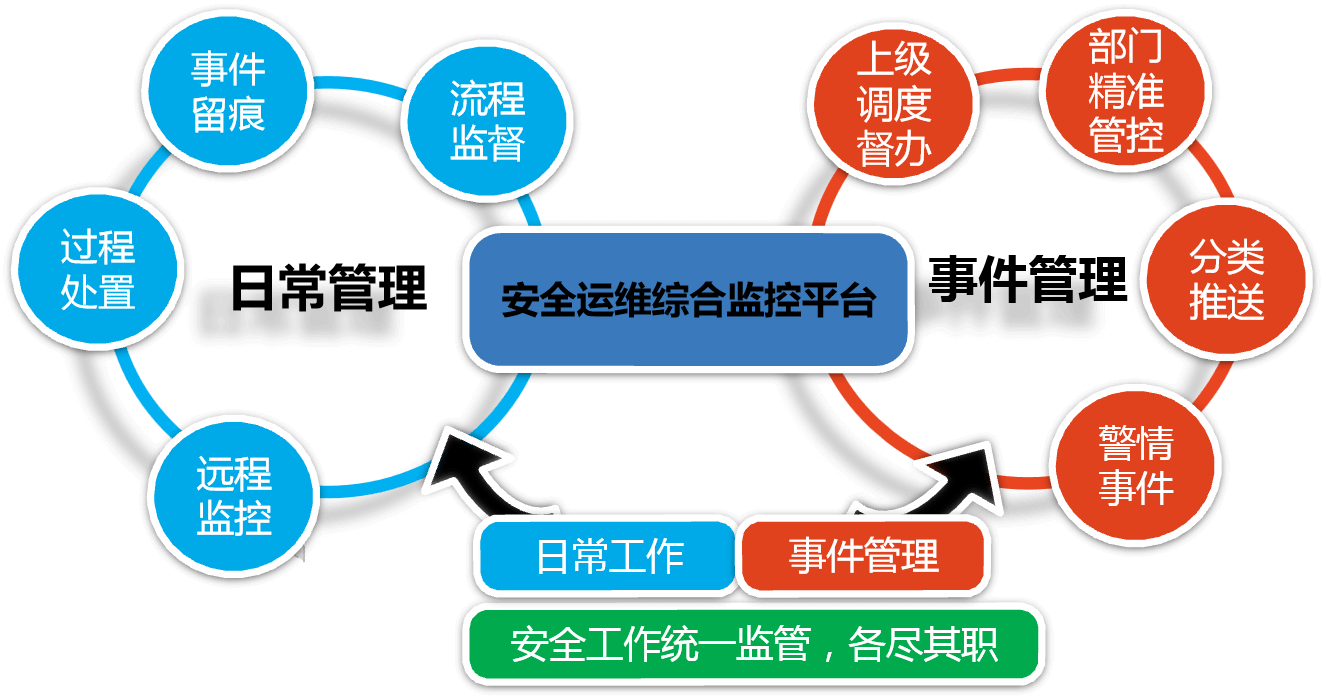
电缆隧道在线监测系统:提升电力设施安全与效率的关键
随着城市化进程的加快,电力电缆隧道在保障城市电力供应方面的地位日益重要。然而,电缆隧道环境复杂,容易受到多种因素影响,如温度、湿度、烟雾、水位等,严重威胁电力设施的安全与稳定运行。在此背景下,电缆…...
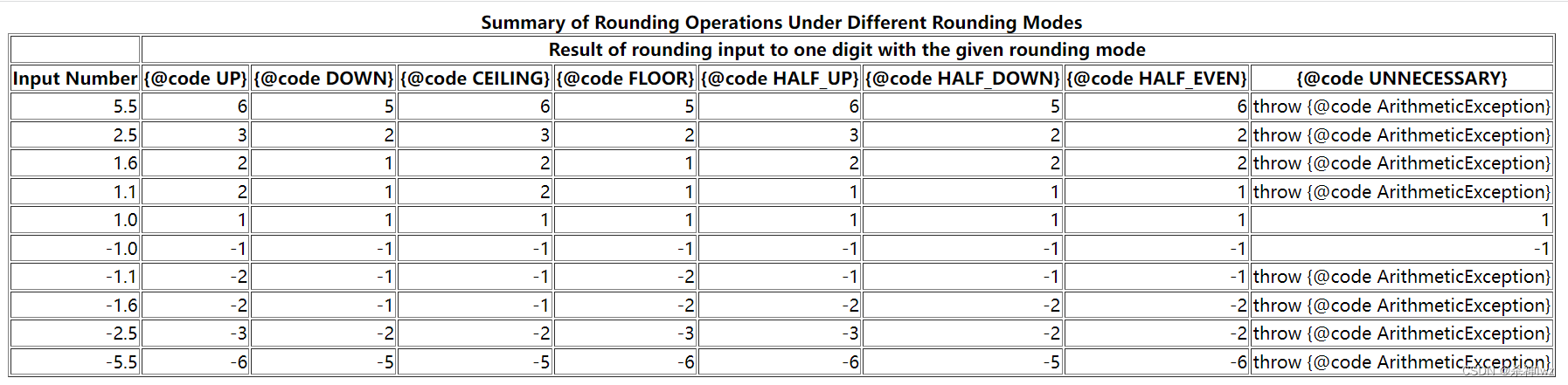
Java BigDecimal 详解
目录 一、BigDecimal 1、简介 2、构造器描述 3、方法描述 4、使用 一、BigDecimal float和double类型的主要设计目标是为了科学计算和工程计算。他们执行二进制浮点运算,这是为了在广域数值范围上提供较为精确的快速近似计算而精心设计的。然而,它…...

简述信息论与采样定理
信息论 香农信息论发表于1948/1949年,它由三部分组成:信号采样、信源编码、信道编码; 信号采样:采样理论研究在何种条件下对连续信号进行采样,从而得到的离散型号可以可逆地恢复出采样前的连续信号。采样得到的离散实…...

网络安全之网站常见的攻击方式
这是作者自学的哈,不算课程内容。 网页中出现大量黑链 网站看着很正常,但是会隐藏一些链接。网页的链接几乎都是标签,这种黑链就是通过链接标签<a></a>或者script在里面链入恶意脚本,等待浏览者的访问,通…...
)
iOS Swift 拍照识别数字(Recognizing Text in Images)
可以用腾讯云 OCR的iOS demo - 腾讯云 苹果官方的解决方案(识别度太低) Recognizing Text in Images - apple developer Extracting phone numbers from text in images(Sample Code) - apple developer import UIKit import Visionclass ViewContro…...

数学建模:智能优化算法及其python实现
数学建模:智能优化算法及其python实现 智能优化算法简介差分进化算法(Differential Evolution,DE)遗传算法(Genetic Algorithm,GA)粒子群优化算法(Particle Swarm Optimization,PSO)模拟退火算法(Simulated Annealing,SA)蚁群算法(Ant Colony Optimization,ACO)…...
monkeyrunner环境搭建和初步用法
一、打开模拟器 运行monkeyrunner之前必须先运行相应的模拟器,不然monkeyrunner无法连接设备。 用Elipse打开Android模拟器或在CMD中用Android命令打开模拟器。这里重点讲一下在CMD中用Android命令打开模拟器 命令:emulator -avd test (注…...
)
2024华为校招面试真题汇总及其解答(一)
1. 我问你点java基础的问题吧,你平时都用什么集合啊,都什么情况下使用 在 Java 中,常用的集合有以下几种: List:有序集合,可以重复,常用实现类有 ArrayList、LinkedList、Vector。Set:无序集合,不能重复,常用实现类有 HashSet、TreeSet。Map:键值对集合,键不能重复…...

css调整字体间距 以及让倾斜字体
调整字体间距 .element {letter-spacing: 2px; /* 调整为适当的值 */ }倾斜字体1 .element {font-style: italic; }请注意,不是所有的字体都有斜体样式可用。如果字体本身没有斜体版本,则可能无法实现完全的斜体效果。 倾斜字体2 <span class"…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
