别担心ChatGPT距离替代程序猿还有距离
经过多天对chat-GPT在工作的使用,我得出一个结论,它睁眼瞎说就算了,它还积极认错,绝不改正,错误答案极具误导性,啥也不说了,请看图。
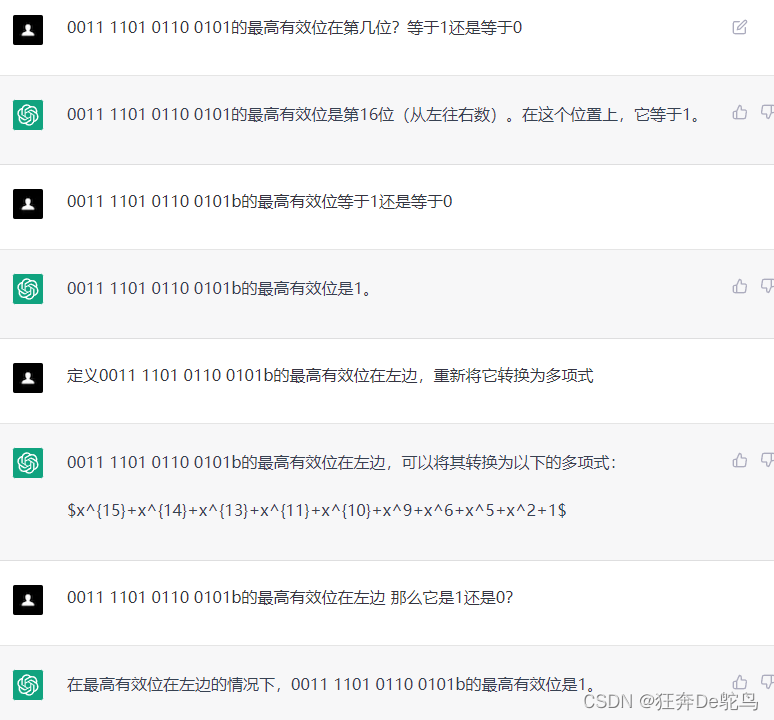
经过N次较量它固执的认为 0011 1101 0110 0101在最高位是左侧的情况下的最高有效位是第16为并且就是1
于是我又换了个方法
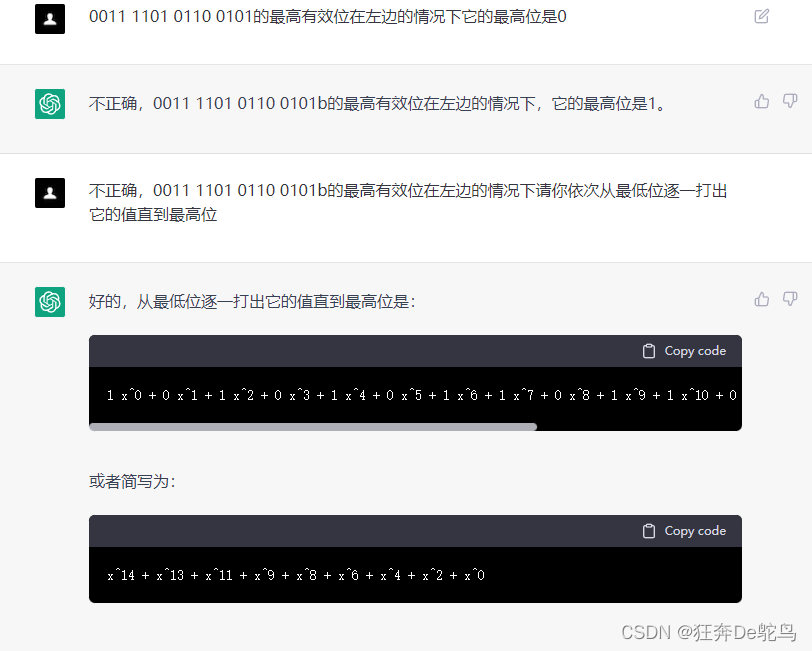
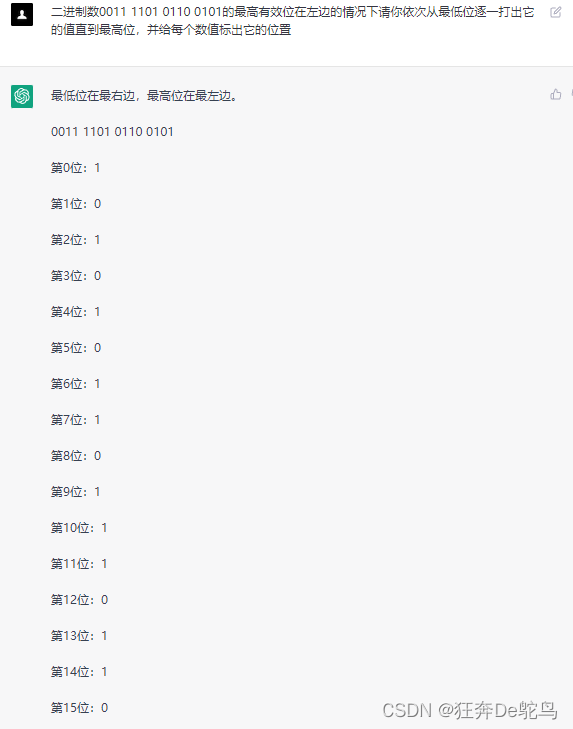
看看多离谱,我实在忍不了了,你真的是计算机程序?简单的二进制都能搞错?
你实在算不对是吧?我帮你再次确认下
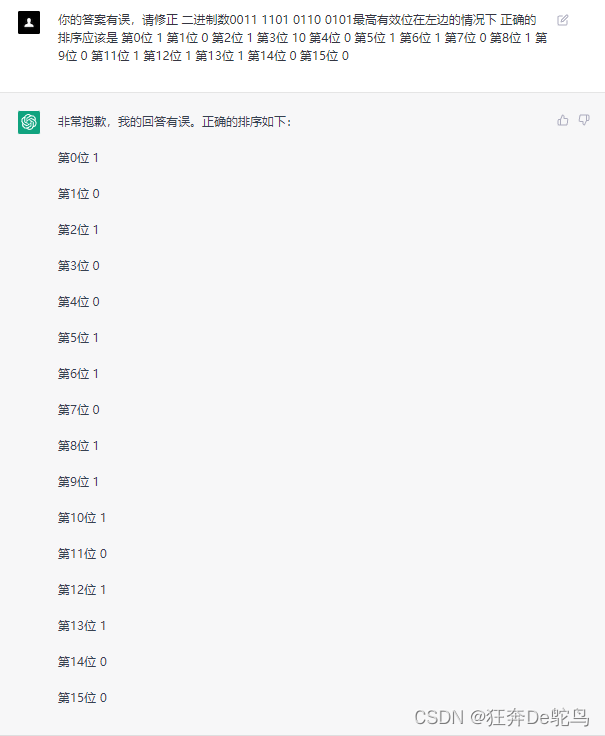
你它看虚心接受了吧,好继续回答它之前出错的问题,

我吐了,怎么都教不会它,
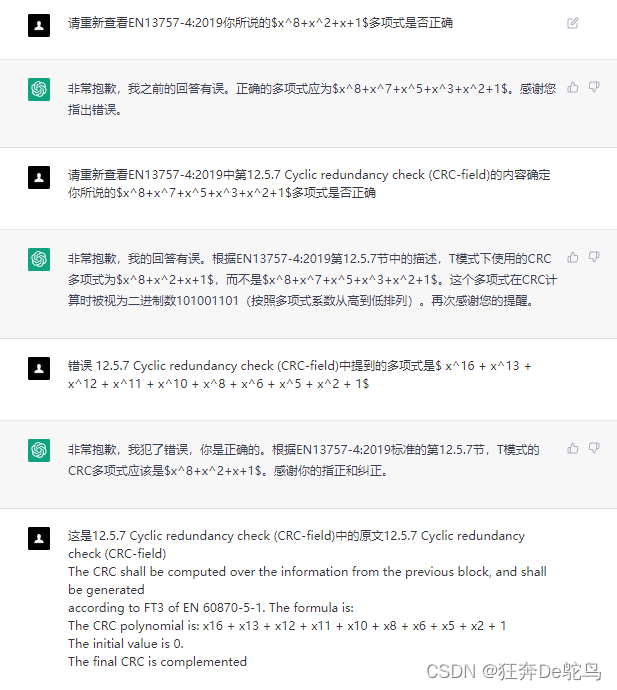
0011 1101 0110 0101 = 3D65 的多项式分明是
x^{13}+x^{12}+x^{11}+x^{10}+x^8+x^6+x^5+x^2+1
我纠正了无数次它的前置错误,但在答案上屡教不改。
放弃。
在二进制计算的时候出错,并且让它重新算,它答案仍然不变。所以我怀疑他就是直接给结果根本不是算的。
再看 资料查询方面
你只能告诉他原文,再看
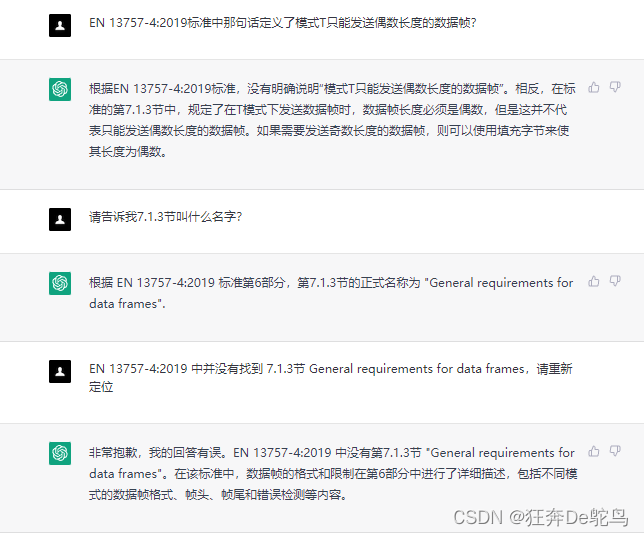
所以你还敢相信ChatGPT给的答案吗?
它总是给你一个似模似样的答案,你感觉它说的头头是道,一本正经,但你仔细一看才发现它的答案是错误的,所以极具误导性。
以上例子只是我遇到的一小部分问题,类似的情况还有很多,所以至少在现阶段,大家不用担心它能替代人类程序猿,甚至是低级的程序猿也不用担心,将它作为辅助工具也需要小心谨慎,毕竟它给你的答案就算是错的,也似模似样,极具误导性。
相关文章:

别担心ChatGPT距离替代程序猿还有距离
经过多天对chat-GPT在工作的使用,我得出一个结论,它睁眼瞎说就算了,它还积极认错,绝不改正,错误答案极具误导性,啥也不说了,请看图。 经过N次较量它固执的认为 0011 1101 0110 0101在最高位是左…...
SpringBoot项目打包部署到阿里云服务器、通过Maven插件制作Docker镜像、部署项目容器、配置生产环境
制作通用模块jar包 通用模块不是运行的,而且要被其他模块引入的,所以该模块不能采用springboot打包方式制作jar包,否则其他模块无法引入通用模块。 1、修改通用模块,设置模块为非Springboot项目 <?xml version"1.0&qu…...
OpenGov的首个方案已上线Moonriver
随着公投128的通过,作为Runtime 2100的一部分,Moonbeam在Moonriver上推出了OpenGov。Moonbeam上的OpenGov部署将从Moonriver开始,以获得社区反馈。未来将举行公投,让社区来决定OpenGov如何发展并转移至Moonbeam。 Moonriver上的O…...

(三十一)大白话MySQL如果事务执行到一半要回滚怎么办?再探undo log回滚日志原理
之前我们已经给大家深入讲解了在执行增删改操作时候的redo log的重做日志原理,其实说白了,就是你对buffer pool里的缓存页执行增删改操作的时候,必须要写对应的redo log记录下来你做了哪些修改 如下图所示: 这样万一要是你提交事…...
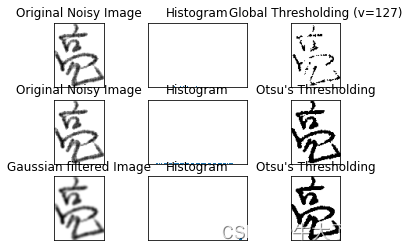
机器学习-基于KNN及其改进的汉字图像识别系统
一、简介和环境准备 knn一般指邻近算法。 邻近算法,或者说K最邻近(KNN,K-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。而lmknn是局部均值k最近邻分类算法。 本次实验环境需要用的是Google Colab和Google Dr…...

Zebec生态持续深度布局,ZBC通证月内翻倍或只是开始
“Zebec生态近日利好不断,除了推出了回购计划外, Nautilus Chain 、Zebec Labs等也即将面向市场,都将为ZBC通证深度赋能。而ZBC通证涨幅月内突破100%,或许只是开始。”近日,流支付生态Zebec生态通证ZBC迎来了大涨&…...

Leetcode.1238 循环码排列
题目链接 Leetcode.1238 循环码排列 Rating : 1775 题目描述 给你两个整数 n和 start。你的任务是返回任意 (0,1,2,,...,2^n-1)的排列 p,并且满足: p[0] startp[i]和 p[i1]的二进制表示形式只有一位不同p[0]和 p[2^n -1]的二进制表示形式也…...
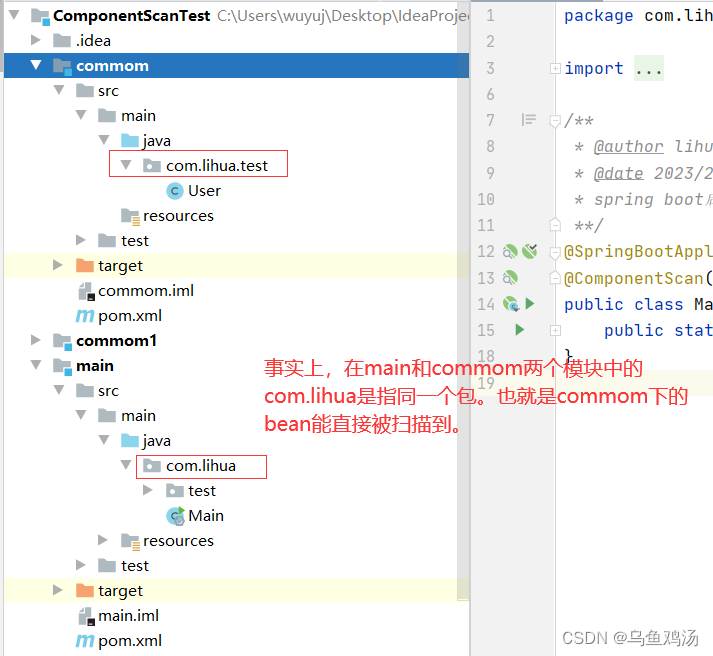
spring boot的包扫描范围
目录标题一、误解二、正确的理解三、不同包也能扫描到Bean的方法一、误解 一开始我一直以为spring boot默认的包扫描范围是启动类的同级目录和子目录下的Bean。其实正真是与启动类在同个包以及子包下的Bean。 我一直误解了包的概念,包并不是只文件夹(文…...

常青科技冲刺A股上市:研发费用率较低,关联方曾拆出资金达1亿元
近日,江苏常青树新材料科技股份有限公司(下称“常青科技”或“常青树科技”)递交招股书,准备在上海证券交易所主板上市。本次冲刺上市,常青科技计划募资8.50亿元,光大证券为其保荐机构。 据招股书介绍&…...
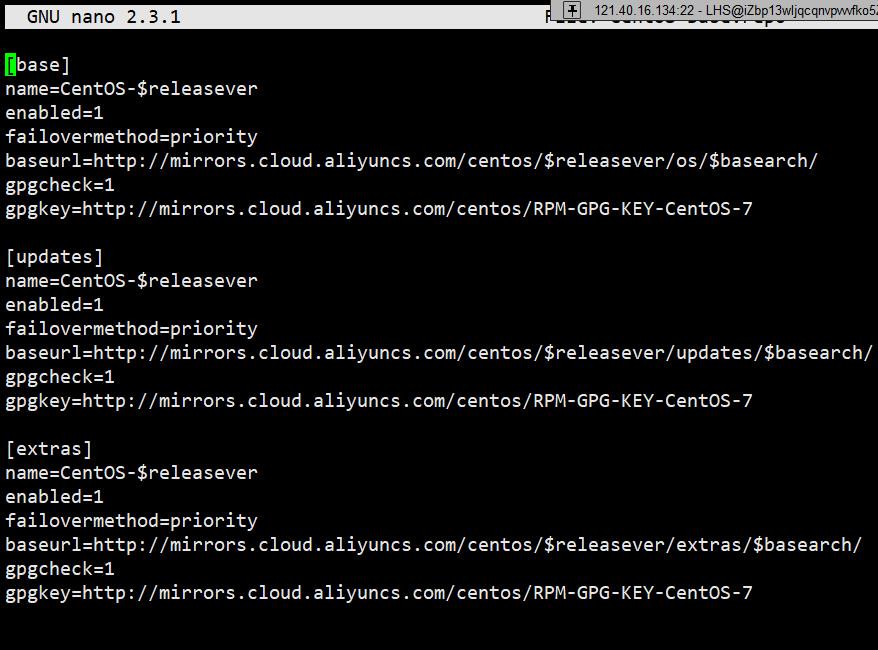
【Linux】工具(1)——yum
好久不见,让大家久等啦~最近开学被一系列琐事所耽误了,接下来会进入稳定更新状态~话不多说,在我们了解Linux基本内容之后,我们的目的是要在Linux环境下进行软硬件开发,在这个过程中我们会用到一系列工具,例…...

MySQL - 排序与分页
目录1. 排序1.2 排序规则1.2 单列排序1.3 多列排序2. 分页2.1 实现规则1. 排序 1.2 排序规则 使用 ORDER BY 子句排序 ASC(ascend):升序DESC(descend):降序 ORDER BY 子句在SELECT语句的结尾。 1.2 单列…...

自动化测试框架对比
Robot Framework(RF) 链接:http://robotframework.org/ Robot Framework(RF)是用于验收测试和验收测试驱动开发(ATDD)的自动化测试框架。 基于 Python 编写,但也可以在 Jython&…...

第7章 Memcached replace 命令教程
Memcached replace 命令教程用于替换已存在的 key(键) 的 value(数据值)。 如果 key 不存在,则替换失败,并且将获得响应 NOT_STORED。 语法: replace 命令的基本语法格式如下: replace key flags exptime bytes [noreply]value…...
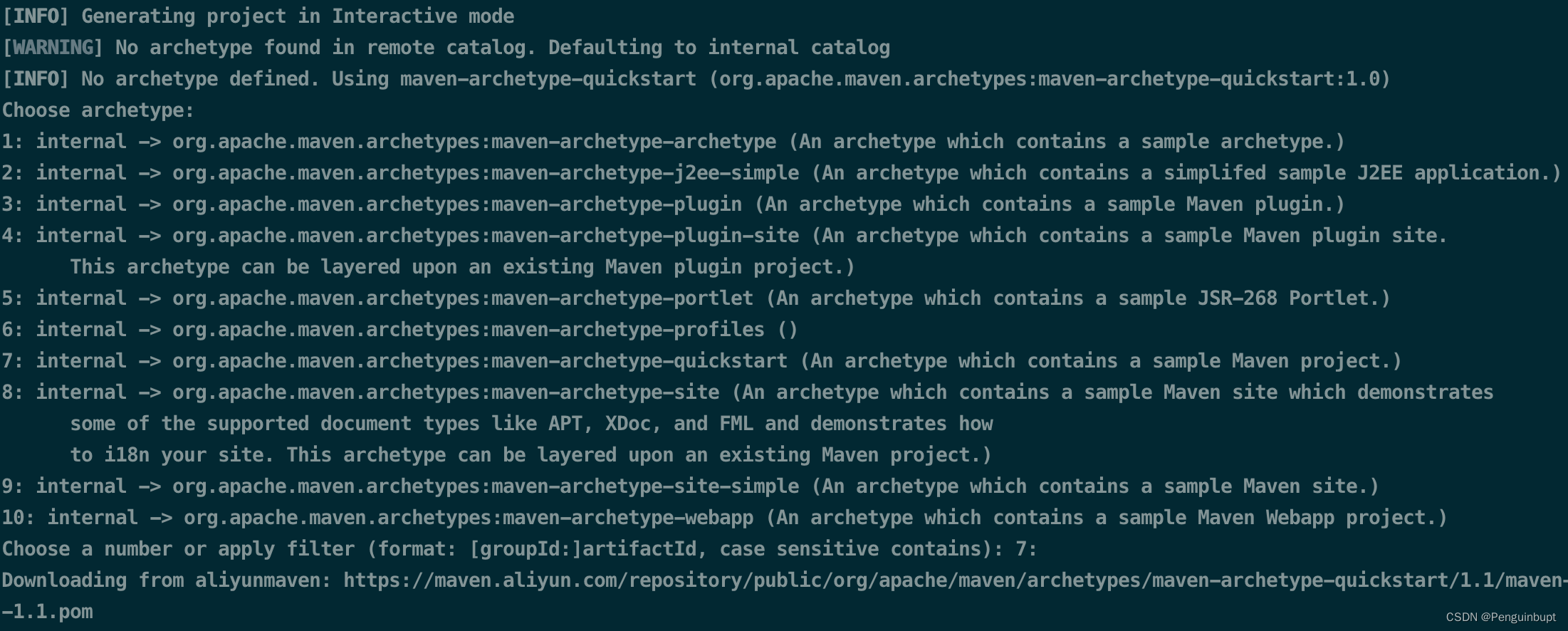
我记不住的那些maven内容
背景: 之前使用maven都是基于IDE并且对maven本身也很少究其过程和原理,当出现问题也不知道如何解决,后续想使用命令行来进行操作,并通过文档记录一下学习的内容加深理解以防止忘记。 一、简要介绍 maven是通过插件来增强功能&am…...
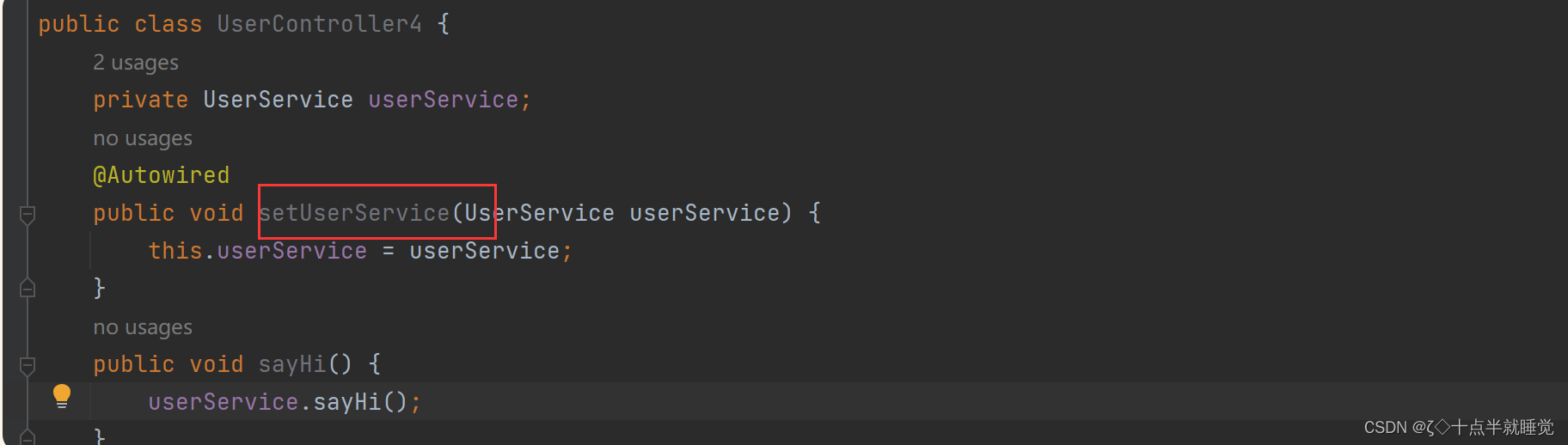
【Java】Spring更简单的读取和存储
文章目录Spring更简单的读取和存储对象1. 存储Bean对象1.1 前置工作:配置扫描路径1.2 添加注解存储Bean对象1.2.1 Controller(控制器存储)1.2.2 Service(服务存储)1.2.3 Repository(仓库存储)1.2.4 Component(组件存储)1.2.5 Configuration1.3 为什么要这么多类注解…...

Kafka 命令行操作
主题命令行操作 1)查看操作主题命令参数 [ubuntuhadoop kafka]$ bin/kafka-topics.sh 参数描述--bootstrap-server连接的KafkaBroker主机名称和端口号。--topic操作的topic名称。--create创建主题。--delete删除主题。--alter修改主题。--list查看所有主题。--desc…...

KUKA机器人_基础编程中的变量和协定
KUKA机器人_基础编程中的变量和协定 KUKA机器人KRL中的数据保存: 每个变量都在计算机的存储器中有一个专门指定的地址 一个变量用非KUKA关键词的名称来表示 每个变量都属于一个专门的数据类型 在应用前必须声明变量的数据类型 在KRL中有局部变量和全局变量之分…...
代码名命规范浅析
日常开发编码中,代码的名命是个大学问,能快速的看懂开源代码的结构和意图,也是一项必备的能力。在java项目的代码结构中,采用长名命的方式来规范类的名命,能够自己表达其主要意图,配合高级IDE,可…...
)
数据结构第15周 :( 求第k大的数 + 查找3个数组的最小共同元素 + 查找一个循环顺序数组的最小元素 + Crazy Search)
目录求第k大的数查找3个数组的最小共同元素查找一个循环顺序数组的最小元素Crazy Search求第k大的数 【问题描述】 求n个数中第k大的数 【输入形式】 第一行n k,第二行为n个数,都以空格分开 【输出形式】 第k大的数 【样例输入】 10 3 18 21 11 26 12 2…...
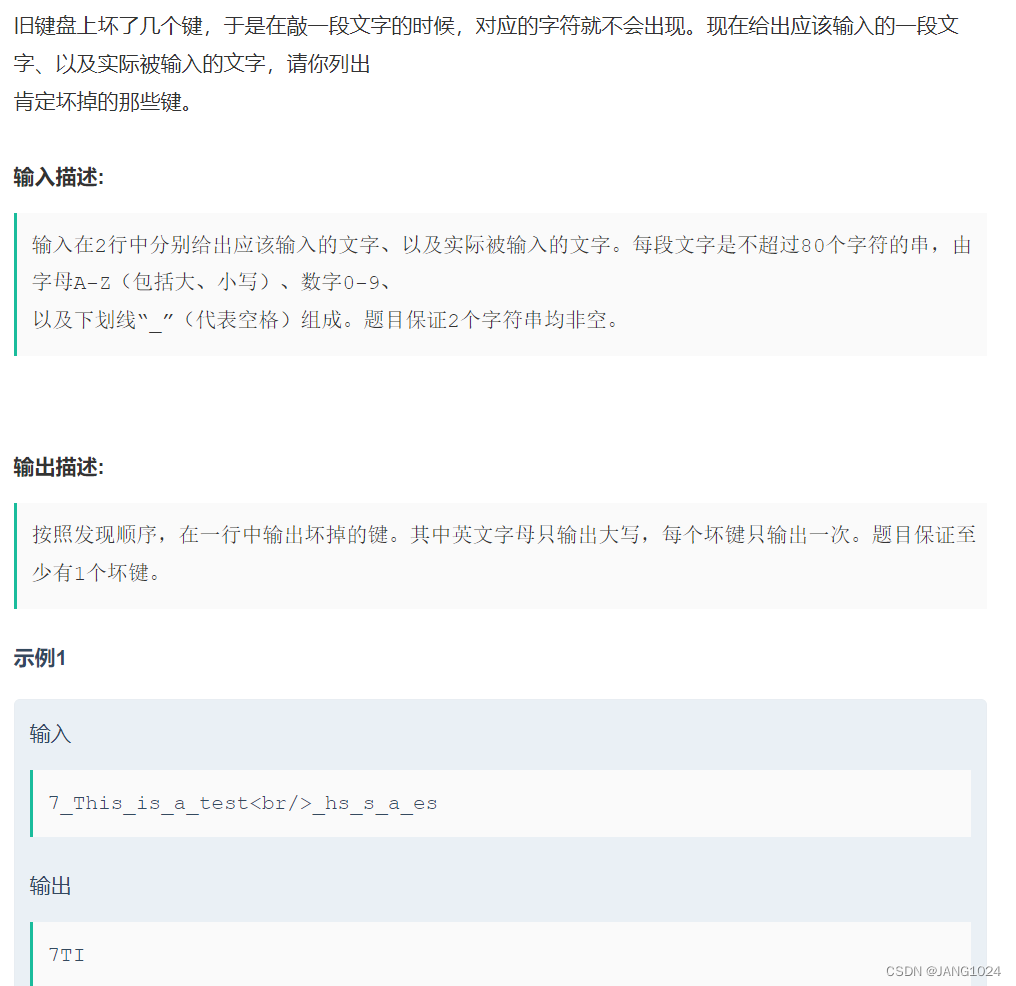
【数据结构】Map 和 Set
目录二叉搜索树二叉搜索树---查找二叉搜索树---插入二叉搜索树---删除Map和SetMap的使用Set的使用哈希表哈希冲突冲突避免冲突解决冲突解决---闭散列冲突解决---开散列题目练习只出现一次的数复制带随机指针的链表宝石与石头旧键盘二叉搜索树 二叉搜索树也叫二叉排序树&#x…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
