MATLAB实现相关性分析
目录
一.基本理论
二.两类相关系数的对比
三.相关系数的假设检验
四.MATLAB的相关操作
五.其他有关的一些列技巧
六.案例展示
七.实战操作
一.基本理论
所谓相关系数,本质上是来衡量两组数据的关系大小——对应呈现函数关心的两种变量,那么我们可以很清楚他们之间的关系;而对于没有强烈关联的变量,我们若无法抽象他们之间的函数,那么可以用相关性强弱来描述他们之间的关系所在。


如上是有关相关系数的计算方式:所谓的皮尔逊相关系数,即为我们本科期间学过的那种,也就是考研数一数三会涉及的部分~

如下是需要注意的一些列理论知识: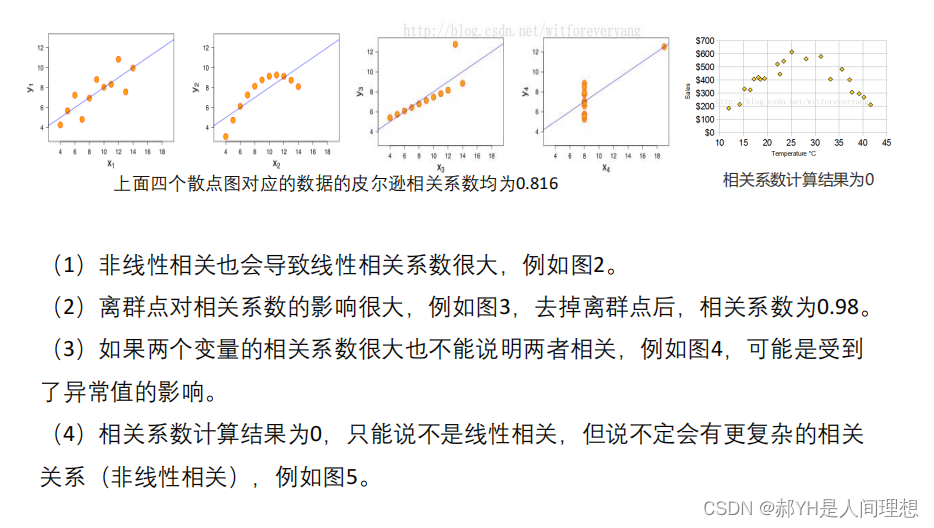 总的来说,当变量之间呈现线性关系时,才有考虑相关系数大小的意义~
总的来说,当变量之间呈现线性关系时,才有考虑相关系数大小的意义~
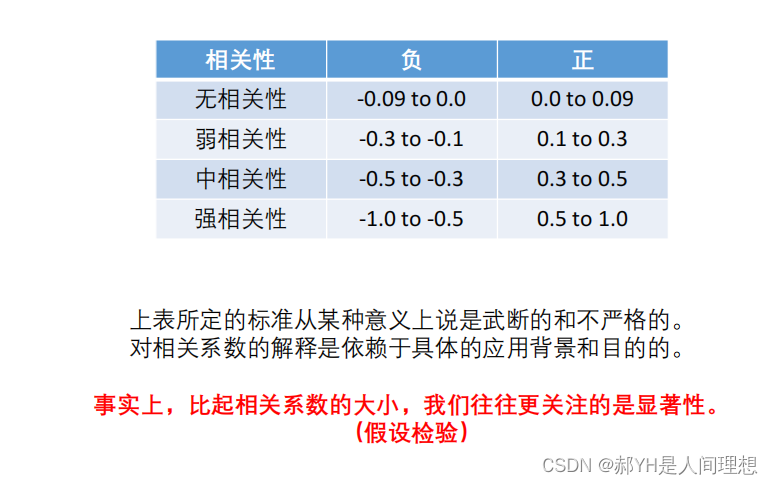
如上是衡量相关性强弱的普遍标准:一般认为相关系数大于0.5时,呈现较强的相关性~
二.两类相关系数的对比
通常我们会接触到皮尔逊相关系数和斯皮尔曼相关系数两种类型。
如下是关于斯皮尔曼相关系数的理论:

 如下是区别方式:
如下是区别方式:

三.相关系数的假设检验
这一部分非常理论,考数一的同学可以稍微研究研究,不过还是以实际操作为重点~

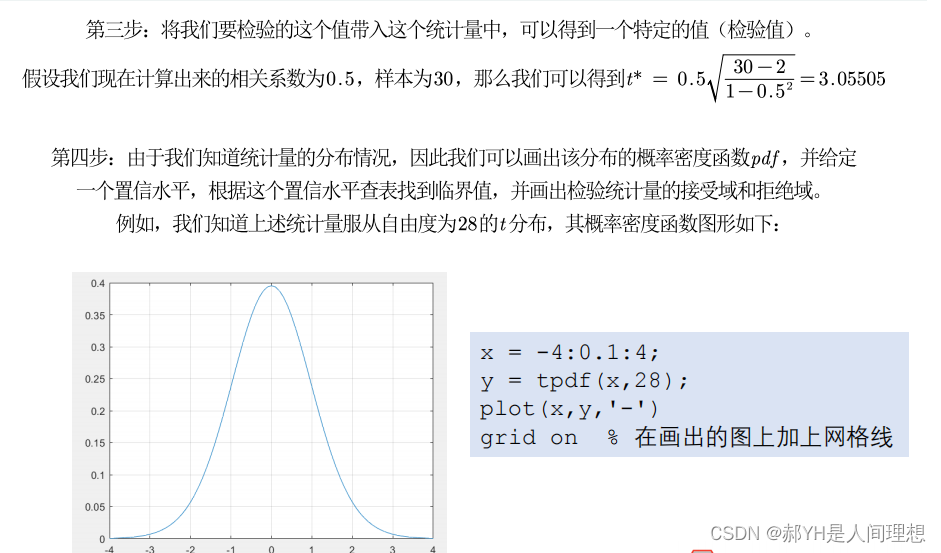

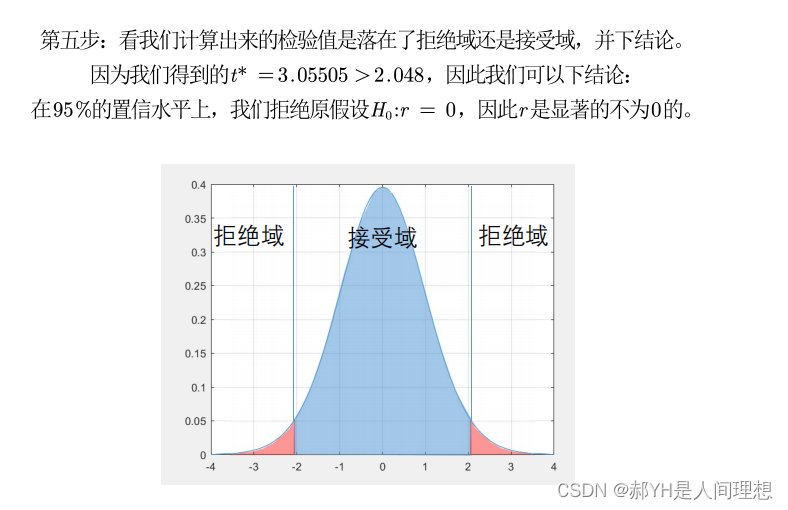
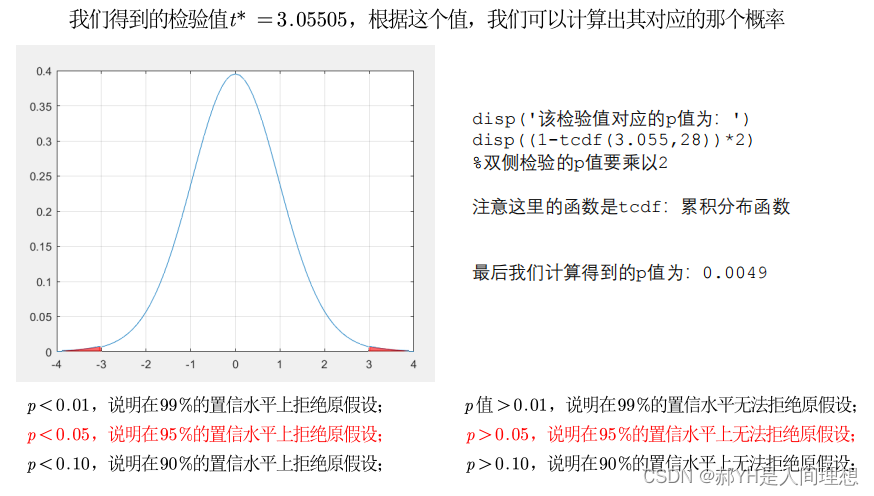
满足假设检验的条件:
第一, 实验数据通常假设是成对的来自于正态分布的总体。 因为我们在求皮尔逊相关性系数以后,通常还会用 t 检验之类的方法来进行皮尔逊相关性系数检验,而 t 检验是基于数据呈正态分布的假设的。第二, 实验数据之间的差距不能太大。 皮尔逊相关性系数受异常值的影响比较大。第三:每组样本之间是独立抽样的。 构造 t 统计量时需要用到。

四.MATLAB的相关操作
如下是20个初二学生的身高及跳远成绩:
| 身高 | 立定跳远 |
| 163 | 208 |
| 158 | 210 |
| 157 | 210 |
| 158 | 210 |
| 157 | 210 |
| 170 | 198 |
| 167 | 180 |
| 160 | 187 |
| 167 | 180 |
| 160 | 187 |
| 170 | 198 |
| 160 | 167 |
| 165 | 190 |
| 162 | 175 |
| 166 | 200 |
| 169 | 179 |
| 159 | 217 |
| 162 | 175 |
| 166 | 200 |
首先介绍一些基本的统计函数:
如下是计算皮尔逊相关系数的代码:
x=[163,158,157,158,157,170,167,160,167,160,170,160,165,162,166,169,159,162,166];
y=[208,210,210,210,210,198,180,187,180,187,198,167,190,175,200,179,217,175,200];
R=corrcoef(x,y);如下代码会返回假设检验要用到的p值:
[R,P]=corrcoef(x,y);如下是正态分布检验用到的代码:
%% 正态分布检验
[hx,px] = jbtest(x,0.05);
[hy,py] = jbtest(y,0.05);
disp(H)
disp(P)如下是计算斯皮尔曼相关系数的代码(通常情况下两种相关系数不一样大):
(注意:x与y必须是列向量)
Rs=corr(x',y','type','Spearman');斯皮尔曼相关系数假设检验的公式:
test=(1-normcdf(Rs*(19-1)^1/2))*2;test值>0.05即无法拒绝原假设。
如上即为操作的基本功。
五.其他有关的一些列技巧
相关技术等统计学问题,用SPSS计算往往更方便,如下图:
勾选自己想要的选项:
计算结果如下:
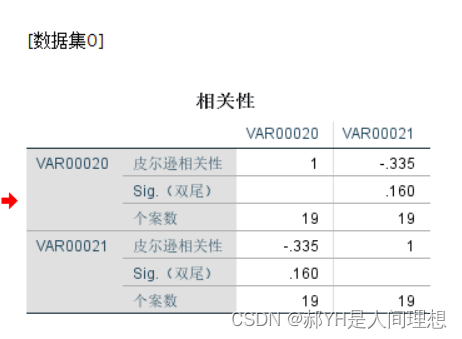
此外,关于热力图的画法,MATLAB种用到函数heatmap(R),其中R即为相关系数矩阵。
此处介绍一种更投机的操作方式——Excel法:
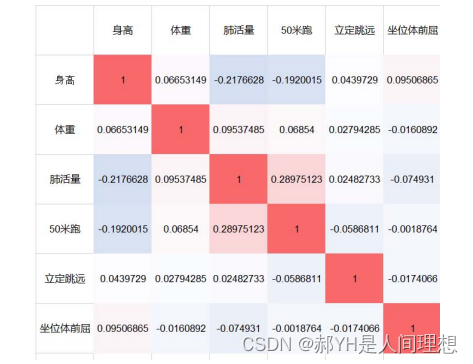
具体的方式就是,把相关系数矩阵沾进Excel中,再将行列大小调成一致——成正方形显示~再根据条件格式设置样式~

六.案例展示
分享在数模和市场调研大赛中用到相关性分析的典例:

 21年亚太赛的案例,当时第一次纯小白,画得属实抽象.........
21年亚太赛的案例,当时第一次纯小白,画得属实抽象.........
 22年华数杯,有进步
22年华数杯,有进步

22国赛选拔赛,渐入佳境

22年国赛,养兵千日用兵一时(写得有点问题,不重要。。。当时已经交了才发现错误)

23年正大杯——这种就是前文提到的Excel法,属实有点low哈哈哈,平时小打小闹无所谓,学术论文尽量还是正经画比较好~
七.实战操作
来做一个实战:很多小伙伴都会关心——考研时名校会不会对本科出身比较有成见呢?我们采用23年WHU电子信息专硕的录取情况来做一个统计~
我们计算4组相关系数:
- 初试成绩与本科出身
- 复试成绩与本科出身
- 初试成绩与录取情况
- 出生与录取情况
其中,我们对本科出身做出如下正向化——即学校越好得分得分越高:
| 学校类型 | 对应数值 |
| 武汉985 | 4 |
| 其他区域985 | 3 |
| 211 | 2 |
| 双非及以下 | 1 |
而是否拟录取使用1和0分别标记。
注意:实际上,处理0-1变量,更适合使用Logistic回归,不过这里为了说明相关性分析的主要思想就凑合用了...
最后得到如下118条数据:
| 序号 | 初试得分 | 复试得分 | 出身 | 录取情况 |
| 1 | 428 | 88.72 | 4 | 1 |
| 2 | 414 | 89.04 | 3 | 1 |
| 3 | 423 | 86.12 | 3 | 1 |
| 4 | 405 | 91.08 | 2 | 1 |
| 5 | 396 | 91.28 | 4 | 1 |
| 6 | 412 | 86.12 | 2 | 1 |
| 7 | 401 | 89.32 | 1 | 1 |
| 8 | 402 | 88.88 | 4 | 1 |
| 9 | 403 | 87.92 | 3 | 1 |
| 10 | 426 | 80.08 | 4 | 1 |
| 11 | 421 | 80.6 | 1 | 1 |
| 12 | 403 | 84.68 | 4 | 1 |
| 13 | 396 | 86.36 | 4 | 1 |
| 14 | 377 | 91.32 | 4 | 1 |
| 15 | 412 | 80.8 | 1 | 1 |
| 16 | 401 | 84 | 3 | 1 |
| 17 | 392 | 86 | 1 | 1 |
| 18 | 394 | 84.72 | 4 | 1 |
| 19 | 384 | 87.16 | 2 | 1 |
| 20 | 402 | 81.4 | 3 | 1 |
| 21 | 391 | 84.68 | 4 | 1 |
| 22 | 384 | 86.68 | 2 | 1 |
| 23 | 387 | 85.28 | 3 | 1 |
| 24 | 385 | 85.64 | 4 | 1 |
| 25 | 392 | 83.32 | 3 | 1 |
| 26 | 409 | 77.16 | 3 | 1 |
| 27 | 370 | 88.68 | 2 | 1 |
| 28 | 393 | 81.52 | 2 | 1 |
| 29 | 402 | 78.76 | 3 | 1 |
| 30 | 371 | 87.8 | 4 | 1 |
| 31 | 363 | 89.88 | 2 | 1 |
| 32 | 371 | 87.4 | 1 | 1 |
| 33 | 363 | 89.64 | 4 | 1 |
| 34 | 356 | 91.64 | 1 | 1 |
| 35 | 370 | 87.36 | 2 | 1 |
| 36 | 361 | 89.72 | 4 | 1 |
| 37 | 394 | 79.76 | 1 | 1 |
| 38 | 374 | 85.48 | 2 | 1 |
| 39 | 377 | 84.36 | 1 | 1 |
| 40 | 360 | 89.4 | 2 | 1 |
| 41 | 380 | 83.36 | 2 | 1 |
| 42 | 377 | 84.24 | 2 | 1 |
| 43 | 388 | 80.92 | 3 | 1 |
| 44 | 360 | 89.32 | 3 | 1 |
| 45 | 389 | 80.44 | 2 | 1 |
| 46 | 364 | 87.88 | 4 | 1 |
| 47 | 368 | 86.04 | 1 | 1 |
| 48 | 388 | 79.84 | 2 | 1 |
| 49 | 356 | 89.4 | 4 | 1 |
| 50 | 381 | 81.8 | 3 | 1 |
| 51 | 374 | 83.36 | 3 | 1 |
| 52 | 371 | 84.2 | 4 | 1 |
| 53 | 383 | 80.6 | 1 | 1 |
| 54 | 369 | 84.76 | 1 | 1 |
| 55 | 367 | 85.32 | 2 | 1 |
| 56 | 386 | 79.4 | 4 | 1 |
| 57 | 377 | 81.48 | 3 | 1 |
| 58 | 359 | 86.88 | 1 | 1 |
| 59 | 376 | 81.64 | 2 | 1 |
| 60 | 371 | 83.12 | 4 | 1 |
| 61 | 376 | 81.32 | 3 | 1 |
| 62 | 375 | 81.6 | 1 | 1 |
| 63 | 355 | 87.48 | 1 | 1 |
| 64 | 375 | 81.24 | 3 | 1 |
| 65 | 361 | 85.32 | 3 | 1 |
| 66 | 361 | 85.04 | 2 | 1 |
| 67 | 369 | 82.6 | 3 | 1 |
| 68 | 365 | 83.64 | 2 | 1 |
| 69 | 358 | 85.56 | 1 | 1 |
| 70 | 369 | 81.8 | 2 | 1 |
| 71 | 372 | 80.88 | 3 | 1 |
| 72 | 364 | 83.24 | 1 | 1 |
| 73 | 365 | 82.68 | 1 | 1 |
| 74 | 366 | 82.36 | 2 | 1 |
| 75 | 359 | 84.12 | 2 | 1 |
| 76 | 372 | 80.12 | 4 | 1 |
| 77 | 365 | 81.96 | 4 | 1 |
| 78 | 359 | 83.72 | 1 | 1 |
| 79 | 357 | 84.2 | 1 | 1 |
| 80 | 363 | 81.72 | 1 | 1 |
| 81 | 366 | 80.56 | 2 | 1 |
| 82 | 355 | 83.64 | 1 | 1 |
| 83 | 356 | 83.32 | 2 | 1 |
| 84 | 383 | 75.08 | 2 | 1 |
| 85 | 373 | 78.04 | 1 | 1 |
| 86 | 372 | 78.32 | 2 | 1 |
| 87 | 360 | 81.88 | 2 | 1 |
| 88 | 385 | 74.28 | 4 | 0 |
| 89 | 357 | 81.92 | 2 | 0 |
| 90 | 392 | 71.4 | 2 | 0 |
| 91 | 365 | 79.12 | 1 | 0 |
| 92 | 361 | 79.48 | 2 | 0 |
| 93 | 378 | 74.2 | 1 | 0 |
| 94 | 380 | 73.28 | 1 | 0 |
| 95 | 370 | 76.16 | 3 | 0 |
| 96 | 359 | 79.4 | 1 | 0 |
| 97 | 371 | 75.44 | 4 | 0 |
| 98 | 359 | 78.32 | 1 | 0 |
| 99 | 367 | 75.68 | 2 | 0 |
| 100 | 357 | 78.2 | 4 | 0 |
| 101 | 361 | 76.48 | 1 | 0 |
| 102 | 362 | 75.6 | 1 | 0 |
| 103 | 394 | 65.56 | 2 | 0 |
| 104 | 394 | 65.52 | 1 | 0 |
| 105 | 387 | 67.56 | 1 | 0 |
| 106 | 377 | 70.16 | 2 | 0 |
| 107 | 370 | 71.8 | 2 | 0 |
| 108 | 359 | 74.8 | 1 | 0 |
| 109 | 361 | 73.56 | 2 | 0 |
| 110 | 362 | 73.2 | 2 | 0 |
| 111 | 358 | 73.96 | 1 | 0 |
| 112 | 358 | 73.88 | 2 | 0 |
| 113 | 355 | 74.4 | 2 | 0 |
| 114 | 368 | 69.32 | 2 | 0 |
| 115 | 355 | 71.96 | 3 | 0 |
| 116 | 356 | 70.88 | 1 | 0 |
| 117 | 367 | 61.52 | 1 | 0 |
| 118 | 360 | 63.08 | 1 | 0 |
直接用MATLAB一个corrcoef搞定,结果如下:
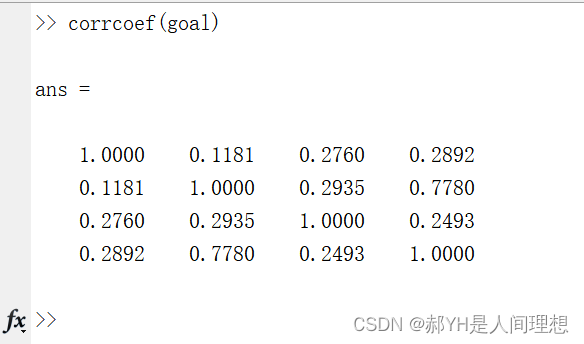
因此得出如下相关系数的结果:
- 初试成绩与本科出身:0.2760
- 复试成绩与本科出身:0.2935
- 初试成绩与录取情况:0.2892
- 出生与录取情况:0.2493
综上,我们可以得出结论:
首先,初试成绩与本科出身的相关性较低,这现实逻辑相一致——初试成绩仅与过去一年你的投入时间成本呈强烈正相关,而与别的面板数据——比如绩点等,没有太大的关系;
此外,复试成绩与本科出身并没有很强的相关性,证明该校不歧视本科出身;
初试成绩与录取情况虽然成较弱的正相关,可能有两个原因——一是模型的严谨性不足,另一方面可能是因为初试成绩占比相对较低(巧合的是复试强相关......),这要不同学校具体分析;
最后,出身与录取情况呈弱相关,说明上岸与否,全掌握在自己手里。
- 天助自助者,望诸君共勉~
相关文章:

MATLAB实现相关性分析
目录 一.基本理论 二.两类相关系数的对比 三.相关系数的假设检验 四.MATLAB的相关操作 五.其他有关的一些列技巧 六.案例展示 七.实战操作 一.基本理论 所谓相关系数,本质上是来衡量两组数据的关系大小——对应呈现函数关心的两种变量,那么我们可以…...
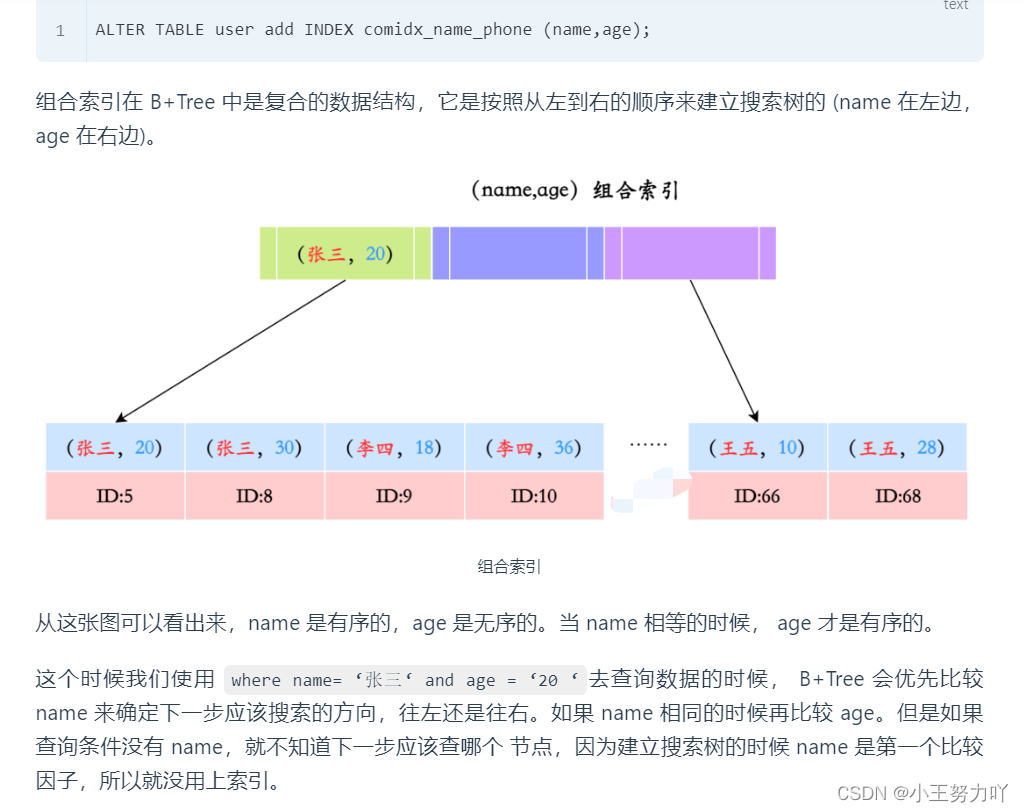
MySQL索引看这篇就够了
能简单说一下索引的分类吗? 例如从基本使用使用的角度来讲: 主键索引: InnoDB 主键是默认的索引,数据列不允许重复,不允许为 NULL,一个表只能有一个主键。唯一索引: 数据列不允许重复,允许为 NULL 值&…...

无法从 /var/lib/rpm 打开软件包数据库
使用yum命令安装软件包时,报错“无法从 /var/lib/rpm 打开软件包数据库” 小白教程,一看就会,一做就成。 1.原因 是误操作导致 rpm 数据库损坏。(/var/lib/rpm 目录下的文件被损坏) 2.解决 当RPM 数据库发生损坏&a…...

路由器实现 IP 子网之间的通信
目录 路由器配置静态或默认路由实现 IP 子网之间的通信 地址聚合与最长前缀匹配路由配置 路由器配置静态或默认路由实现 IP 子网之间的通信 按如下拓扑图配置 其中,路由器加入4GEW-T PC配置如下 LSW1的配置 <Huawei>sys Enter system view, return user…...
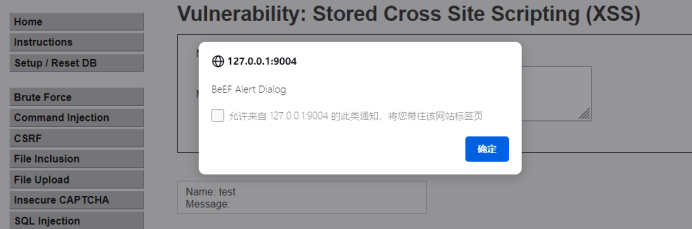
解决kali beef启动失败问题及实战
文章目录 一、解决方法二、靶场实战应用1.首先打开dvwa这个靶场,设置难度为low2.打开xss-stored3.准备payload4.提交payload5.利用 一、解决方法 首先需卸载 ruby apt remove ruby 卸载 beef apt remove beef-xss 重新安装ruby apt-get install ruby apt-get insta…...
【NetEq】NackTracker 走读
重传列表的最大限制是500个包,大约10秒钟 // A limit for the size of the NACK list.static const size_t kNackListSizeLimit = 500; // 10 seconds for 20 ms frame// packets.允许设置一个小于max_nack_list_size的值 // Set a maximum for the size of the NACK list. I…...
)
条例18~23(设计与声明)
目录 条例18 让接口被正确使用,不易被误用 总结 条例19 设计class犹如设计type 条例20 宁以const的引用传参替代传值传参 总结 条例21 必须返回对象时,别妄想返回他的引用 总结 条例22 将成员变量声明为private 总结 条例23 宁以非友元非…...
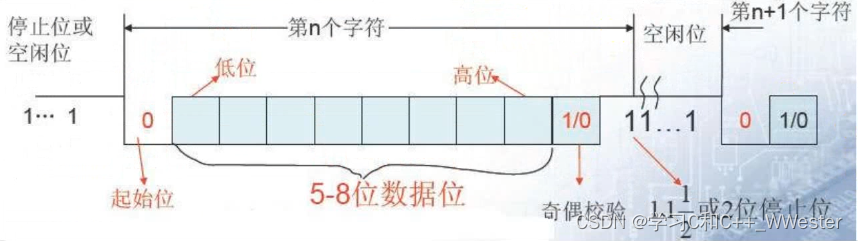
STM32 UART通信协议 基础知识
通用异步收发器(Universal Asynchronous Receiver/Transmitter),通常称作UART,是一种串行、异步、全双工的通信协议。 在通信领域中,有两种数据通信方式:并行通信和串行通信。串口的数据传输是以串行方式进行的。串口在…...

nginx部署vue前端项目,访问报错500 Internal Server Error
前言 描述:当我配置好全部之后,通过 服务器 ip 地址访问,遇到报错信息:500 Internal Server Error。 情况说明 前提:我是通过Docker启动nginx容器,通过-v 绑定数据卷,将html文件和nginx.conf…...

@Excel注解
在 Java 开发中,Excel 注解通常用于标记实体类的字段,以指示与 Excel 文件的导入和导出相关的配置信息。 Excel 注解通常是自定义的注解,它可以包含多个属性,用于定义与 Excel 相关的配置,如字段的标题、顺序、数据格…...

解释器模式简介
概念: 解释器模式(Interpreter Pattern)是一种行为型设计模式,它用于定义语言的文法,并解析和执行给定语言中的表达式。该模式将每个表达式表示为一个类,并提供了一种方式来组合这些表达式以实现复杂的语句…...

图像识别技术在不同场景下有哪些应用?
图像识别技术在不同场景下的应用包括: 遥感图像识别:航空遥感和卫星遥感图像通常用图像识别技术进行加工以便提取有用的信息。该技术目前主要用于地形地质探查,森林、水利、海洋、农业等资源调查,灾害预测,环境污染监…...

阿里巴巴OceanBase介绍
前言 官网地址:https://www.oceanbase.com/ OceanBase是由蚂蚁集团完全自主研发的国产原生分布式数据库,始创于2010年。是全球唯一在 TPC-C 和 TPC-H 测试上都刷新了世界纪录的国产原生分布式数据库。 2010年,创始人阳振坤加入阿里巴巴&…...

leetcode 2560. 打家劫舍 IV
2560. 打家劫舍 IV 沿街有一排连续的房屋。每间房屋内都藏有一定的现金。现在有一位小偷计划从这些房屋中窃取现金。 由于相邻的房屋装有相互连通的防盗系统,所以小偷 不会窃取相邻的房屋 。 小偷的 窃取能力 定义为他在窃取过程中能从单间房屋中窃取的 最大金额 。…...

正点原子lwIP学习笔记——Socket接口TCP实验
1. Socket接口TCP Client配置连接 配置步骤如下所示: sin_family设置为AF_INET表示IPv4网络协议;sin_port为设置端口号;sin_addr. s_addr设置远程IP地址;调用函数Socket创建Socket连接, 注意该函数的第二个参数SOCK_…...
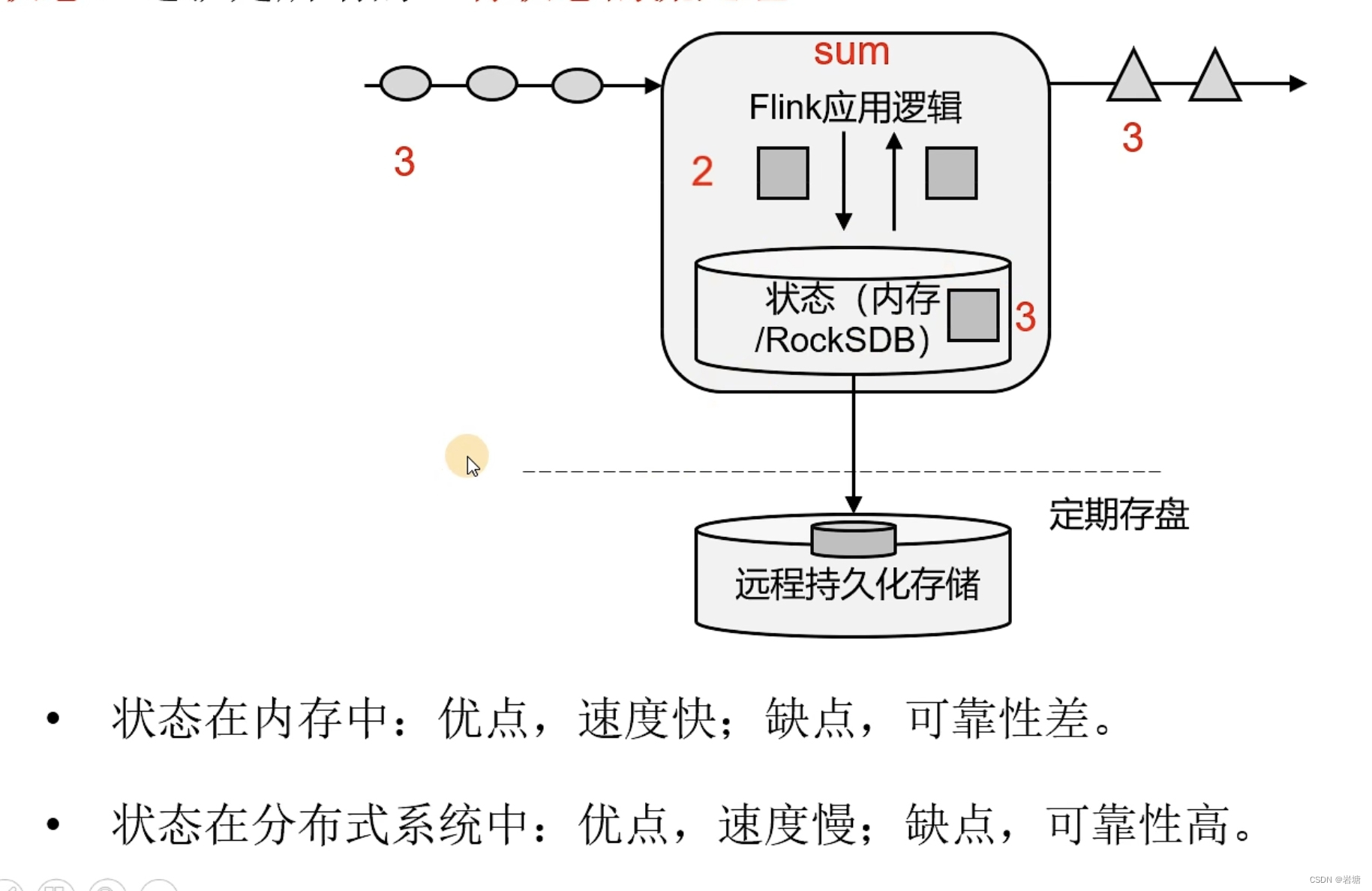
【Flink】
事件驱动型应用 核心目标:数据流上的有状态计算 Apache Flink是一个框架和分布式处理引擎,用于对无界或有界数据流进行有状态计算。 运行逻辑 状态 把流处理需要的额外数据保存成一个“状态”,然后针对这条数据进行处理,并且更新状态。这就是所谓的“…...

大数据Flink(九十一):Array Expansion(数组列转行)和Table Function(自定义列转行)
文章目录 Array Expansion(数组列转行)和Table Function(自定义列转行)...
华为云云耀云服务器L实例评测|华为云云耀云服务器L实例CentOS的存储和备份策略
1 华为云云耀云服务器L实例介绍 华为云云耀云服务器L实例是华为云计算服务中的一种虚拟云服务器,它提供了强大的计算资源,可以在云端运行各种应用程序和服务。 华为云服务器提供了多种实例类型,包括通用型、计算优化型、内存优化型等&#…...
Web自动化测试 —— 如何进行Selenium页面数据及元素交互?啊哈
前言: Web自动化测试是一种常用的测试方式,通过在浏览器中模拟用户操作以及与页面元素的交互,可以有效地检验页面的功能性以及稳定性。Selenium是一款流行的Web自动化测试工具,在本篇文章中,我们将介绍如何使用Seleni…...
)
点云从入门到精通技术详解100篇-基于全景图的室内场景点云补全方法(续)
目录 3.3 模型训练及实验评估 3.3.1 模型训练 3.3.2实验评估 4 基于自...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
