代码随想录笔记--动态规划篇
1--动态规划理论基础
动态规划经典问题:① 背包问题;② 打家劫舍;③ 股票问题; ④ 子序列问题;
动态规划五部曲:
① 确定 dp 数组及其下标的含义;
② 确定递推公式;
③ 确定 dp 数组的初始化;
④ 确定遍历顺序,一般为从左到右;
⑤ 打印 dp 数组,一般用于检查;
2--斐波那契数

主要思路:
经典动态规划,dp[i] 表示第 i 个数的斐波那契数;递推公式为:dp[i] = dp[i-1] + dp[i - 2];初始化dp[0] = 1,dp[1] = 1;遍历顺序从左到右;
#include <iostream>
#include <vector>class Solution {
public:int fib(int n) {if(n <= 1) return n;std::vector<int> dp(n+1, 0);dp[0] = 0; dp[1] = 1;for(int i = 2; i <= n; i++){dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};int main(int argc, char argv[]){int test = 2;Solution S1;int res = S1.fib(test);std::cout << res << std::endl;return 0;
}
3--爬楼梯
主要思路:
经典动态规划,dp[i] 表示到达第 i 阶楼梯的方法数;递推公式为 dp[i] = dp[i - 1] + dp[i - 2];初始化dp[1] = 1, dp[2] = 2;遍历顺序从左到右;
#include <iostream>
#include <vector>class Solution {
public:int climbStairs(int n) {if(n <= 2) return n; std::vector<int> dp(n+1, 0);dp[1] = 1, dp[2] = 2;for(int i = 3; i <= n; i++){dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};int main(int argc, char argv[]){int n = 2;Solution S1;int res = S1.climbStairs(n); std::cout << res << std::endl;return 0;
}
4--使用最小花费爬楼梯

主要思路:
dp[i] 表示到达第 i 阶楼梯需要的最小花费;初始化 dp[0] = 0, dp[1] = 0,因为可以从 0 和 1 出发,因此不需要花费;递推公式为 dp[i] = std::min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);默认从左到右遍历;
#include <iostream>
#include <vector>class Solution {
public:int minCostClimbingStairs(std::vector<int>& cost) {std::vector<int> dp(cost.size()+1, 0); // 到达第i阶的最小花费dp[0] = 0;dp[1] = 0;for(int i = 2; i <= cost.size(); i++){dp[i] = std::min(cost[i-2]+dp[i-2], cost[i-1]+dp[i-1]);}return dp[cost.size()];}
};int main(int argc, char argv[]){// cost = [1,100,1,1,1,100,1,1,100,1]std::vector<int> cost = {1, 100, 1, 1, 1, 100, 1, 1, 100, 1};Solution S1;int res = S1.minCostClimbingStairs(cost);std::cout << res << std::endl;return 0;
}
5--不同路径

主要思路:
dp[i][j] 表示到达 (i, j) 位置的路径数,初始化两个边界 dp[i][0] = 1,dp[0][j] = 1;状态转移方程为:dp[i][j] = dp[i-1][j] + dp[i][j-1];遍历顺序为从上到下,从左到右;
#include <iostream>
#include <vector>class Solution {
public:int uniquePaths(int m, int n) {std::vector<std::vector<int>> dp(m, std::vector<int>(n, 0));// 初始化for(int i = 0; i < m; i++) dp[i][0] = 1;for(int j = 0; j < n; j++) dp[0][j] = 1;// 遍历for(int r = 1; r < m; r++){for(int c = 1; c < n; c++){dp[r][c] = dp[r-1][c] + dp[r][c-1];}}return dp[m-1][n-1];}
};int main(int argc, char argv[]){// m = 3, n = 7int m = 3, n = 7;Solution S1;int res = S1.uniquePaths(m, n);std::cout << res << std::endl;return 0;
}
6--不同路径II

主要思路:
与上题类似,dp[i][j] 表示到达 (i, j) 位置的路径数,初始化两个边界 dp[i][0] = 1,dp[0][j] = 1(确保边界没有障碍物,有障碍物初始化为0);状态转移方程为:(i, j)不是障碍物则 dp[i][j] = dp[i-1][j] + dp[i][j-1],(i, j)为障碍物则dp[i][j] = 0;遍历顺序为从上到下,从左到右;
#include <iostream>
#include <vector>class Solution {
public:int uniquePathsWithObstacles(std::vector<std::vector<int>>& obstacleGrid) {int m = obstacleGrid.size(), n = obstacleGrid[0].size();if(obstacleGrid[m-1][n-1] == 1) return 0;std::vector<std::vector<int>> dp(m, std::vector<int>(n, 0));// 初始化for(int i = 0; i < m && obstacleGrid[i][0] != 1; i++) dp[i][0] = 1;for(int j = 0; j < n && obstacleGrid[0][j] != 1; j++) dp[0][j] = 1;// 遍历for(int r = 1; r < m; r++){for(int c = 1; c < n; c++){if(obstacleGrid[r][c] == 1) dp[r][c] = 0; // 障碍else dp[r][c] = dp[r-1][c] + dp[r][c-1];}}return dp[m-1][n-1];}
};int main(int argc, char argv[]){// obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]std::vector<std::vector<int>> test = {{0, 0, 0}, {0, 1, 0}, {0, 0, 0}};Solution S1;int res = S1.uniquePathsWithObstacles(test);std::cout << res << std::endl;return 0;
}
7--整数拆分

主要思路:
dp[i] 表示整数 i 拆分后的最大乘积;初始化dp[0] = 0, dp[1] = 0, dp[2] = 1; 状态转移方程为:dp[i] = max(dp[i], max(j*(i-j), j * dp[i-j]));
#include <iostream>
#include <vector>class Solution {
public:int integerBreak(int n) {std::vector<int> dp(n+1, 0);// 初始化dp[0] = 0, dp[1] = 0, dp[2] = 1;// 遍历for(int i = 3; i <= n; i++){for(int j = 0; j <= i/2; j++){dp[i] = std::max(dp[i], std::max(j*(i-j), j * dp[i-j]));}}return dp[n];}
};int main(int argc, char argv[]){// n = 10int test = 10;Solution S1;int res = S1.integerBreak(test);std::cout << res << std::endl;return 0;
}
8--不同的二叉搜索树
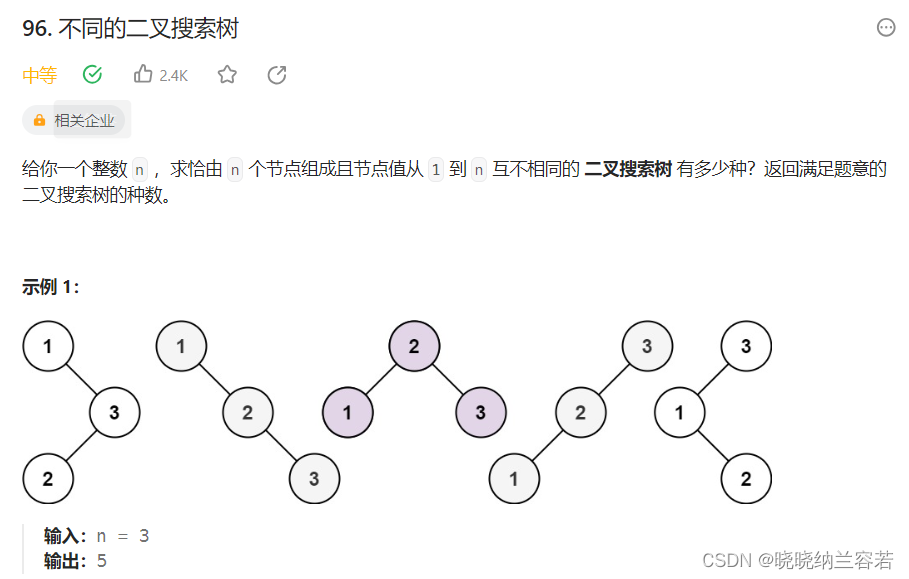
主要思路:
dp[i] 表示由 i 个数字构成的不同二叉搜索树的数目;
初始化:dp[0] = 1;
状态转移方程:dp[i] += dp[j-1] * dp[i-j],0 <= j <= i;其中 dp[j-1] 来构成 j 的左子树,dp[i-j] 来构成 j 的右子树;
遍历顺序:两个 for 循环,第 1 个 for 循环遍历 1 - n,第二个 for 循环遍历 1 - i;
#include <iostream>
#include <vector>class Solution {
public:int numTrees(int n) {std::vector<int> dp(n+1, 0);// 初始化dp[0] = 1;// 遍历for(int i = 1; i <= n; i++){for(int j = 1; j <= i; j++){dp[i] += dp[j-1] * dp[i-j];}}return dp[n];}
};int main(int argc, char *argv[]) {// n = 3int test = 3;Solution S1;int res = S1.numTrees(test);std::cout << res << std::endl;return 0;
}9--
相关文章:

代码随想录笔记--动态规划篇
1--动态规划理论基础 动态规划经典问题:① 背包问题;② 打家劫舍;③ 股票问题; ④ 子序列问题; 动态规划五部曲: ① 确定 dp 数组及其下标的含义; ② 确定递推公式; ③ 确定 dp 数组…...

vue之vuex
Vuex 是 Vue.js 的一个状态管理模式和库,为应用中的所有组件提供了一个集中式的存储管理,并提供了一种强大的方式来管理应用的状态。Vuex 包含以下核心概念: State:定义了应用的状态,类似于组件中的 data。 Getters&a…...
)
ISO 26262 系列学习笔记 ———— ASIL定义(Automotive Safety Integration Level)
文章目录 介绍严重度(Severity)暴露概率(Probability of Exposure)可控性(Controllability) 介绍 如果没有另行说明,则应满足ASIL A、B、C和D各分条款的要求或建议。这些要求和建议参考了安全目…...

代码随想录 第8章 二叉树
1、理论知识 (1)、满二叉树 如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树。 (2)、完全二叉树 除了底层节点可能没有填满,其余每层的节点…...
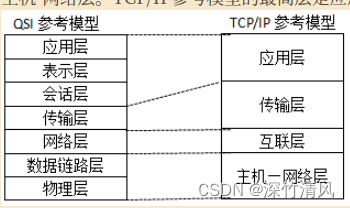
计算机网络工程师多选题系列——计算机网络
2 计算机网络 2.1 网络技术基础 题型1 TCP/IP与ISO模型的问题 TCP/IP由IETF制定,ISO由OSI制定; TCP/IP分为四层,分别是主机-网络层、互联网络层、传输层和应用层;OSI分为七层,分别是物理层、数据链路层、网络层(实…...
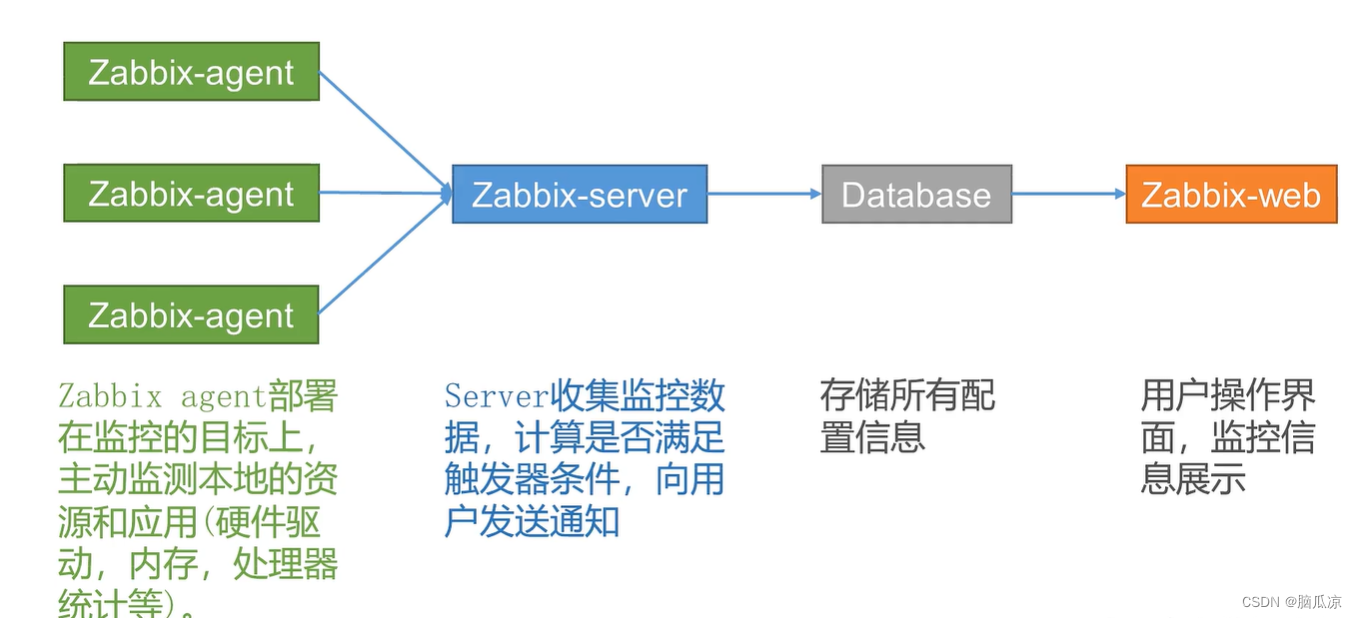
Zabbix5.0_介绍_组成架构_以及和prometheus的对比_大数据环境下的监控_网络_软件_设备监控_Zabbix工作笔记001
z 这里Zabbix可以实现采集 存储 展示 报警 但是 zabbix自带的,展示 和报警 没那么好看,我们可以用 grafana进行展示,然后我们用一个叫睿象云的来做告警展示, 会更丰富一点. 可以看到 看一下zabbix的介绍. 对zabbix的介绍,这个zabbix比较适合对服务器进行监控 这个是zabbix的…...
Spring | 事件监听器应用与最佳实践
引言 在复杂的软件开发环境中,组件之间的通信和信息交流显得尤为重要。Spring框架,作为Java世界中最受欢迎的开发框架之一,提供了一种强大的事件监听器模型,使得组件间的通信变得更加灵活和解耦。本文主要探讨Spring事件监听器的…...

正点原子lwIP学习笔记——NETCONN接口简介
1. NETCONN接口简介 NETCONN API 使用了操作系统的 IPC 机制, 对网络连接进行了抽象,使用同一的接口完成UDP和TCP连接。 NETCONN API接口是在RAW接口基础上延申出来的一套API接口 首先会调用netconn_new创建一个pcb控制块,其实际是一个宏定…...
PHP自动识别采集何意网址文章正文内容
在做PHP采集内容时,用过querylist采集组件,但是这个插件采集页面内容时,都必须要写个采集选择器。这样比较麻烦,每个文章页面都必须指定一条采集规则 。就开始着手找一个插件可以能自动识别任意文章url正文内容并采集的࿰…...

区块链实验室(27) - 区块链+物联网应用案例
分享最新的区块链物联网应用案例:HPCLS-BC...
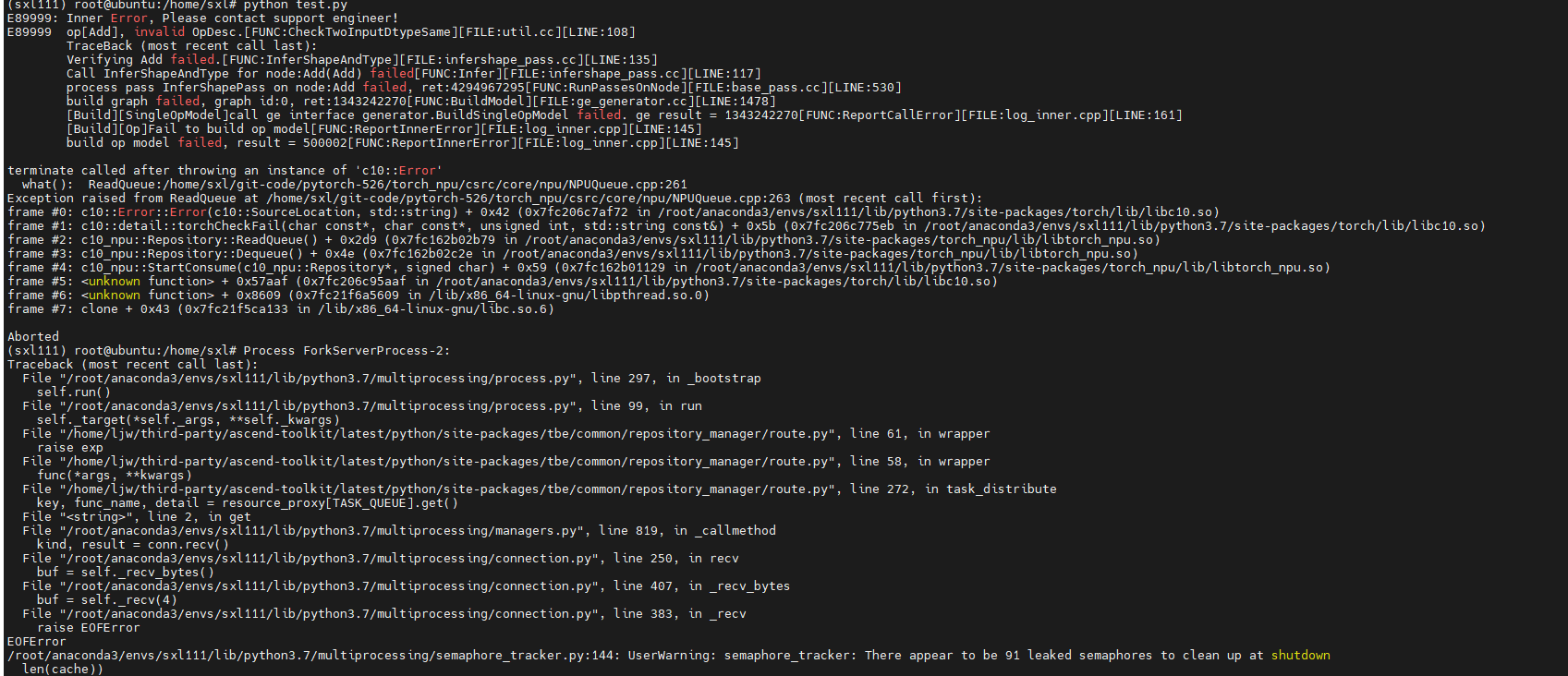
NPU上PyTorch模型训练问题案例
在昇腾AI处理器上训练PyTorch框架模型时,可能由于环境变量设置问题、训练脚本代码问题,导致打印出的堆栈报错与实际错误并不一致、脚本运行异常等问题,那么本期就分享几个关于PyTorch模型训练问题的典型案例,并给出原因分析及解决…...

出现 conda虚拟环境默认放在C盘 解决方法
目录 1. 问题所示2. 原理分析3. 解决方法3.1 方法一3.2 方法二1. 问题所示 通过conda配置虚拟环境的时候,由于安装在D盘下,但是配置的环境默认都给我放C盘 通过如下命令:conda env list,最后查看该环境的确在C盘下 2. 原理分析 究其根本原因,这是因为默认路径没有足够的…...

Ubuntu Postgresql开机自启动服务
1. 建立service文件 sudo vim /etc/systemd/system/postgresql.service2. postgresql service文件 [Unit] DescriptionPostgreSQL 14 database server Documentationman:postgres(1) Documentationhttp://www.postgresql.org/docs/14/static/ Afternetwork.target[Service] T…...

COTS即Commercial Off-The-Shelf 翻译为“商用现成品或技术”或者“商用货架产品”
COTS 使用“不再做修理或改进”的模式出售的商务产品 COTS即Commercial Off-The-Shelf 翻译为“商用现成品或技术”或者“商用货架产品”,指可以采购到的具有开放式标准定义的接口的软件或硬件产品,可以节省成本和时间。 中文名 商用现成品或技术 外文…...
idea开发Springboot出租车管理系统VS开发mysql数据库web结构java编程计算机网页源码maven项目
一、源码特点 springboot 出租车管理系统是一套完善的完整信息系统,结合springboot框架和bootstrap完成本系统,对理解JSP java编程开发语言有帮助系统采用springboot框架(MVC模式开发), 系统具有完整的源代码和数据…...

Linux nohup
nohup 命令用于在 Linux 中将命令或程序在后台运行,并且在终端关闭后仍然保持运行。 nohup命令 描述 nohup 命令用于将命令或程序以不受终端挂断影响的方式在后台运行。 语法 nohup command [arguments] &参数 command:要在后台运行的命令或程…...
Linux 常见问题
1. 使用 sudo 命令时,提示 is not in the sudoers file. 是由于对应用户没有添加到 sudoers 文件中,可以在该文件中指定用户权限。运行以下命令即可打开该文件: visudo 添加上对应用户的权限 Ctrl x 退出保存即可。 2. Debian 新建的普通用…...

仕达利恩飞讯软件TPM设备管理项目正式启动,向数字化再迈一步
9月25日,仕达利恩(惠州)科技有限公司(以下简称“仕达利恩”)设备智能数采项目启动会成功召开,仕达利恩首席崔浩渊、杨翠琼次长携项目主要负责人共同出席本次启动会。为解决仕达利恩现阶段生产过程中的设备管理、设备配件仓管理以及…...
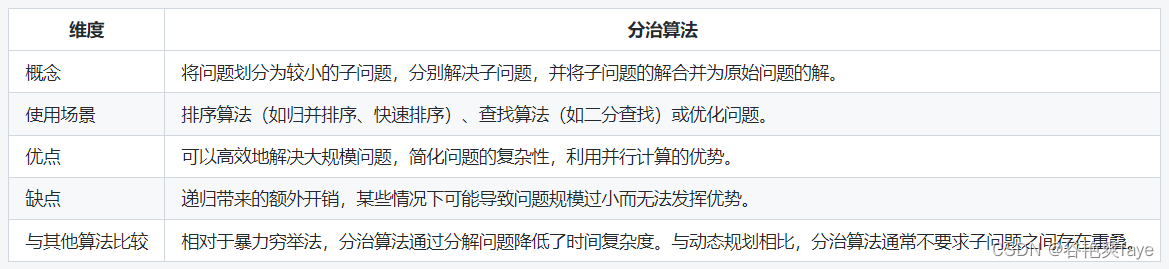
【算法】分治法
文章目录 概念原理和步骤代码示例 总结 概念 分治法(Divide and Conquer)是一种算法设计策略,其思想是将一个大问题划分为若干小规模的子问题,然后递归地解决每个子问题,并将它们的解合并起来以得到原始问题的解。分治…...
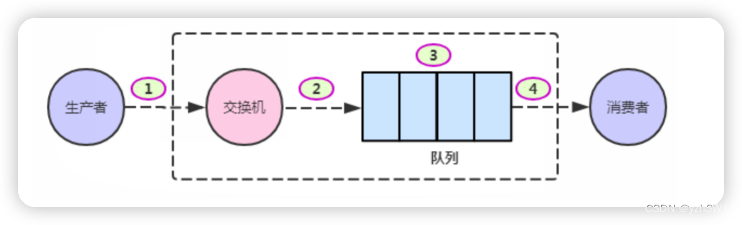
Rabbit消息的可靠性
生产者重连 消费者重试 Confirm模式简介 消息的confirm确认机制,是指生产者投递消息后,到达了消息服务器Broker里面的exchange交换机,则会给生产者一个应答,生产者接收到应答,用来确定这条消息是否正常的发送到Broker…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
