美丽塔O(n)解法单调栈
题目
见上一篇: 较难算法美丽塔时间复杂度O(n)-CSDN博客
时间复杂度
O(n)
分析
接着上篇。从左向右依次处理Left,处理Left[i]时,从右向左寻找第一个符合maxHeights[j]<maxHeights[i]的j。如果j1<j2,且maxHeights[j1]>=maxHeights[j2],那j1永远不会被选到。比如:{1,3,2,4,5},由于2在3右边,且小于3,则无论如何不会选中3。{1,2,2.....},后面无论有什么数,都不会选中第一个2,要么是其他数,要么是第二个2。
可以用栈实现,入栈maxHeights[i]之前,先出栈大于等于maxHeights[i]的数,剩余的都小于maxHeights[i]的数。也就是栈按升序排序的。由于maxHeights[i]和heights[i]都可以通过索引查询,栈中只需要记录索引。
Right类似,不再累赘。
样例分析
| maxHeights | Left的栈情况 |
| {1,2,3,4,5} | 1 12 123 1234 12345 |
| {5,4,3,2,1} | 5 4 3 2 1 |
| {1,2,4,3,5} | 1 12 124 123 1235 |
| {3,1,2} | 3 1 12 |
| {2,1,3} | 2 1 13 |
代码
核心代码
class Solution {
public:long long maximumSumOfHeights(vector<int>& maxHeights) {m_c = maxHeights.size();m_vLeft.resize(m_c);m_vRight.resize(m_c);{//处理左边stack<int> sta;//记录做边的索引for (int i = 0; i < m_c; i++){const auto& h = maxHeights[i];while (sta.size() && (maxHeights[sta.top()] >= h)){sta.pop();//左边比右边大,不会被选中}if (sta.size()){m_vLeft[i] = m_vLeft[sta.top()] + (long long)h * (i - sta.top());}else{m_vLeft[i] = (long long)h * (i -(-1) );}sta.emplace(i);}}{//处理右边stack<int> sta;//记录做边的索引for (int i = m_c - 1; i >= 0; i--){const auto& h = maxHeights[i];while (sta.size() && (maxHeights[sta.top()] >= h)){sta.pop();//左边比右边大,不会被选中}if (sta.size()){m_vRight[i] = m_vRight[sta.top()] + (long long)h * (sta.top()-i);}else{m_vRight[i] = (long long)h * (m_c-i);}sta.emplace(i);}}long long llRet = 0;for (int i = 0; i < m_c; i++){//假定i是山顶 long long llCur = m_vLeft[i] + m_vRight[i] - maxHeights[i];llRet = max(llRet, llCur);}return llRet;}int m_c;vector<long long> m_vLeft, m_vRight;
};测试用代码
class CDebug : public Solution
{
public:
long long maximumSumOfHeights(vector<long long>& maxHeights, vector<long long>& vLeft, vector<long long>& vRight)
{
vector<int> maxs(maxHeights.begin(), maxHeights.end());
long long llRet = Solution::maximumSumOfHeights(maxs);
for (int i = 0 ; i < vLeft.size();i++ )
{
assert(m_vLeft[i] == vLeft[i]);
assert(m_vRight[i] == vRight[i]);
}
//调试用代码
std::cout << "Left: ";
for (int i = 0; i < m_c; i++)
{
std::cout << m_vLeft[i] << " ";
}
std::cout << std::endl;
std::cout << "Right: ";
for (int i = 0; i < m_c; i++)
{
std::cout << m_vRight[i] << " ";
}
std::cout << std::endl;
return llRet;
}
};
int main()
{
vector < vector<vector<long long>>> param = { {{1,2,3,4,5} ,{1,3,6,10,15},{5,8,9,8,5}} ,
{{5,4,3,2,1},{5,8,9,8,5},{15,10,6,3,1}} ,
{{1,2,4,3,5},{1,3,7,9,14},{5,8,10,6,5}},
{{3,1,2}, {3,2,4},{5,2,2}},
{{2,1,3},{2,2,5},{4,2,3}},
{{1000000000,1000000000,1000000000},{1000000000,2000000000,3000000000LL},{3000000000LL,2000000000,1000000000}} };
for (auto& vv : param)
{
auto res = CDebug().maximumSumOfHeights(vv[0], vv[1], vv[2]);
}
//auto res = Solution().maxPalindromes("rire", 3);
//CConsole::Out(res);
}
测试环境
Win10,VS2022 C++17
下载
源码: 【免费】美丽塔单调栈O(n)解法资源-CSDN文库
doc 讲解排版好:【免费】闻缺陷则喜算法册(9月24增加美丽塔)资源-CSDN文库
相关文章:
解法单调栈)
美丽塔O(n)解法单调栈
题目 见上一篇: 较难算法美丽塔时间复杂度O(n)-CSDN博客 时间复杂度 O(n) 分析 接着上篇。从左向右依次处理Left,处理Left[i]时,从右向左寻找第一个符合maxHeights[j]<maxHeights[i]的j。如果j1<j2,且maxHeights[j1]&g…...
的PDF文件压缩软件PDF Squeezer mac中文版软件特点
PDF Squeezer mac是一款macOS平台上的PDF文件压缩软件,可以帮助用户快速地压缩PDF文件,从而减小文件大小,使其更容易共享、存储和传输。PDF Squeezer使用先进的压缩算法,可以在不影响文件质量的情况下减小文件大小。 PDF Squeezer…...

JS Ajax 封装
ajax 封装 一、 什么是Ajax?二、 Ajax的优缺点?2.1 优点2.2 缺点 三、 Ajax的使用3.1 状态码3.2 xhr的基本使用3.3 ajax原生封装:3.3.1 触发GET请求:3.3.2 调用POST请求: 四、Ajax的约束 一、 什么是Ajax? …...

观测云产品更新 | 优化日志数据转发、索引绑定、基础设施自定义等
观测云更新 日志 数据转发:新增外部存储转发规则数据查询;支持启用/禁用转发规则;绑定索引:日志易新增标签绑定,从而实现更细颗粒度的数据范围查询授权能力。 基础设施 > 自定义 【默认属性】这一概念更改为【必…...

trio ValueEvent
class AsyncValue(Generic[T]): 值包装器,提供等待值或过渡的能力。 概要: >>> a AsyncValue(0) # 注意:可以包装任何类型(枚举,元组,...) >>> ... >>> a.valu…...

js 新学一招,点击出现弹框,点击其他地方关闭弹框
文章目录 需求分析 需求 鼠标点击菜单,出现二级菜单,当点击其他地方时,二级菜单自动关闭 分析 <template><el-popoverv-model"visible"></el-popover> </template> <script> export default {dat…...

c#扩展包-Stateless
准备 Stateless是一个有限状态机扩展包。在c#项目中可以直接通过NuGet安装。 使用他需要先用枚举写好你所有可能的状态和子状态。 例如移动,下蹲,空闲,跳跃,游泳,奔跑,走路。 其中,奔跑和走路…...
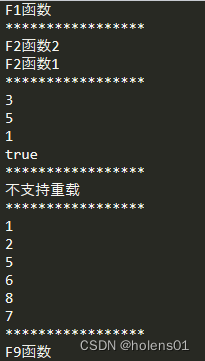
Lua函数
--函数--无参无返回值 function F1()print("F1函数") end F1() print("*****************")--有参 function F2(a)print("F2函数"..a) end F2(2) --如果传入参数和函数数量不一致 --不会报错只是补空 F2(1,2) print("*****************&quo…...
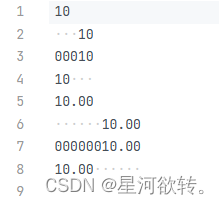
左对齐和右对齐
%d默认为左对齐,%5d为左对齐(以空格补齐),%05d为左对齐(以0补齐),%-5d右补齐(以空格补齐),整数和小数同理。%.xf,x为小数点后保留的位数。 #include<stdi…...
高仿互站网站源码 后台手机端两套模板 电脑端二十套模版
高仿互站网 后台手机端两套模板 电脑端二十套模版,简单介绍几个功能, 支持用户注册开店 开店申请,支持用户发布自己商品 支持卡密形式或实物形式, 支持用户自己发布求助 任务大厅功能,源码完整 更多功能自己去发现吧…...
Spring Controller内存马
获取当前上下文运行环境 getCurrentWebApplicationContext WebApplicationContext context ContextLoader.getCurrentWebApplicationContext(); 在SpringMVC环境下获取到的是一个XmlWebApplicationContext类型的Root WebApplicationContext: 在Spring MVC环境中…...
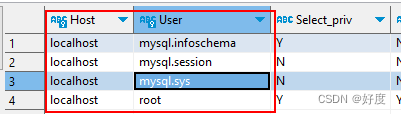
Mysql004:用户管理
前言:本章节讲解的是mysql中的用户管理,包括(管理数据用户)、(控制数据库的访问权限)。 目录 1. 查询用户 2. 创建用户 3. 修改用户密码 4. 删除用户 5. 权限控制 1. 查询用户 在mysql数据库中࿰…...
研究现状)
计算机视觉与深度学习 | 视觉里程计(Visual Odometry,VO)研究现状
===================================================== github:https://github.com/MichaelBeechan CSDN:https://blog.csdn.net/u011344545 ===================================================== 视觉里程计(Visual Odometry,VO) 研究背景及意义视觉里程计国内外研…...
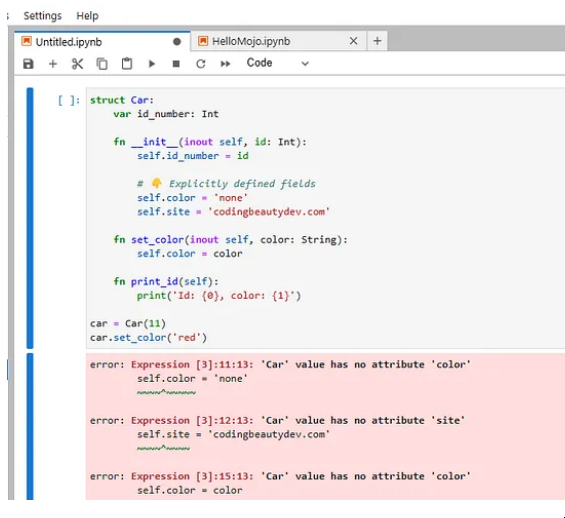
Mojo:新型AI语言中的7个令人惊叹的Python升级,用简单的英语解释人工智能
Mojo:新型AI语言中的7个令人惊叹的Python升级 编程之美 用简单的英语解释人工智能 编程之美 由Coding Beauty设计的图像,使用Mojo标志和Python标志。 它比C更快,与Python一样简单,但速度提高了35000倍。 进入Mojo:一种…...
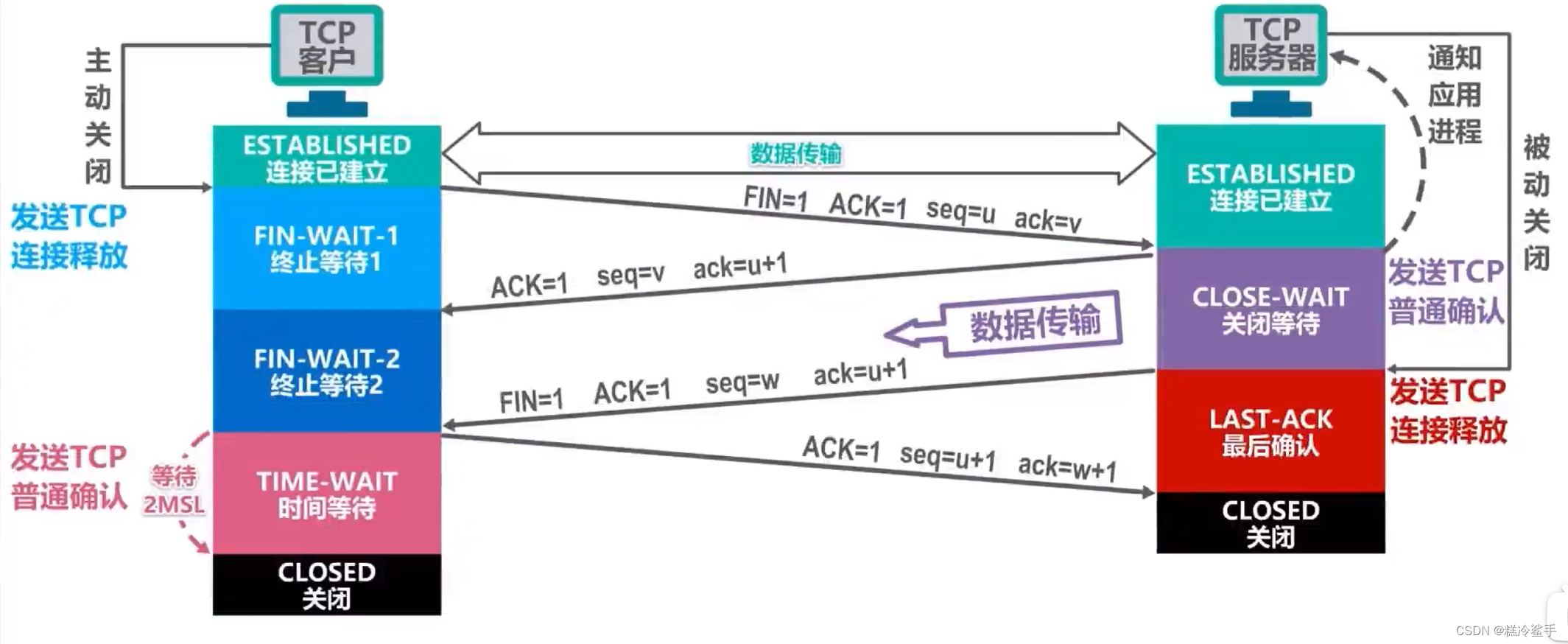
TCP连接的三次握手与四次挥手【重点】
TCP的运输连接管理概述 TCP是面向连接的协议,它基于运输连接来传送TCP报文段 TCP运输连接的建立和释放是每一次面向连接的通信中必不可少的过程 TCP运输连接有以下三个阶段 TCP的运输连接管理就是使运输连接的建立和释放都能正常的进行 TCP建立连接的三次握手&a…...

重生奇迹MU新手玩家如何快速熟悉游戏
新手玩家必须掌握什么呢,建议新手玩家去官方网站上面看看游戏的详细介绍,必须要好的熟悉游戏的各种玩法,让玩家可以有一个初步的认识。 所以这方面是非常重要的,建议每位重生奇迹MU玩家都应该注重这些东西。下面我们就来简单介绍…...
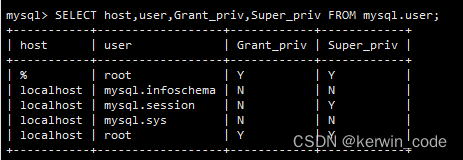
MySQL 用户权限和远程访问设置
目录 一、用户操作查看当前拥有用户创建用户修改用户密码删除用户给root用户开放外网访问 二、用户权限操作授予权限的原则查看授予用户的权限给用户添加权限回收权限 一、用户操作 先要使用root用户登录MySQL后在执行后面操作 查看当前拥有用户 SELECT host,user,Grant_pri…...

Golang基础之关键字
Type 参考 ## https://blog.csdn.net/SHELLCODE_8BIT/article/details/122837699 type有如下几种用法: 定义结构体定义接口类型定义类型别名类型查询 类型定义 type Celsius float64 // 摄氏温度 type Fahrenheit float64 // 华氏温度const (AbsoluteZeroC Cels…...

DataFrame插入多列PerformanceWarning: DataFrame is highly fragmented.
DataFrame插入多列PerformanceWarning: DataFrame is highly fragmented. dataframe列比较多,增加列的代码如下: dfpd.DataFrame() for i in range(1000):vlist[]for j in range(1000):vlist.append(j) df[COL_ str(i)] vlistdf警告错误&#x…...
Springboot登录验证的统一拦截处理
在进行Springboot项目开发的时候如何把每次请求都要验证的用户进行提取拦截统一处理 背景 如果不进行统一的拦截处理,其实这是一个非常痛苦的一件事情,因为每次用户请求你都要去进行用户的信息(用户信息存储在session中)的验证&…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
