day-56 代码随想录算法训练营(19)动态规划 part 16
538.两个字符串的删除操作
思路一:
- 1.dp存储:以word1[i-1]结尾,word2[j-1]结尾,最少进行dp[i][j]次操作
- 2.动态转移方程: if(word1[i-1]==word2[i-1]) dp[i][j]=dp[i-1][j-1];
- else dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1)
- 3.初始化:dp[i][0]=i dp[0][j]=j
- 4.遍历顺序:1~尾巴
class Solution {
public:int minDistance(string word1, string word2) {int n=word1.size(),m=word2.size();vector<vector<int>>dp(n+1,vector<int>(m+1,0));for(int i=0;i<=n;i++) dp[i][0]=i;//相同时需要删除所有字符串for(int j=0;j<=m;j++) dp[0][j]=j;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];//不需要操作else dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);//两个字符串各自的操作取最小}}return dp[n][m];}
};72.编辑距离
思路:
- 1.dp存储:以word1[i]结尾,word2[j]结尾,使两个字符串相同的最小操作次数
- 2.动态转移方程: if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];
- else dp[i][j]=min(dp[i-1][j-1]+1,min(dp[i-1][j]+1,dp[i][j-1]+1)
- 3.初始化:dp[i][0]=i dp[0][j]=j
- 4.遍历顺序:1~n 1~m
class Solution {
public:int minDistance(string word1, string word2) {int n=word1.size(),m=word2.size();vector<vector<int>>dp(n+1,vector<int>(m+1,0));for(int i=0;i<=n;i++) dp[i][0]=i;for(int j=0;j<=m;j++) dp[0][j]=j;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){//添加和删除都是一样的,两边各添加和删除;改变就是上一次的值+1if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];else dp[i][j]=min(dp[i-1][j-1]+1,min(dp[i-1][j]+1,dp[i][j-1]+1));}}return dp[n][m];}
};相关文章:
动态规划 part 16)
day-56 代码随想录算法训练营(19)动态规划 part 16
538.两个字符串的删除操作 思路一: 1.dp存储:以word1[i-1]结尾,word2[j-1]结尾,最少进行dp[i][j]次操作2.动态转移方程: if(word1[i-1]word2[i-1]) dp[i][j]dp[i-1][j-1]; else dp[i][j]min(dp[i-1][…...

蓝桥等考Python组别四级005
第一部分:选择题 1、Python L4 (15分) 字符“0”的ASCII码值为48,则字符“5”的ASCII码值为( )。 3953120240正确答案:B 2、Python L4 (15分) 下面哪个是Python中正确的变量名?( ) ABC#sup01Trueif正确答案:B...

【Linux】diff 命令
【Linux】diff 命令——并排格式输出 功能 diff 以逐行的方式,比较文本文件的异同处。 如果指定要比较目录,则 diff 会比较目录中相同文件名的文件,但不会比较其中子目录 diff [参数] [文件A] [文件B]diff [参数] [目录A] [目录B]【参数】…...

【51单片机】9-定时器和计数器
1.定时器的介绍 1.什么是定时器 (1)SoC的一种内部的外设【在单片机里面,但是在CPU外面】 (2)定时器就是CPU的”闹钟“ 2.什么是计数器 (1)定时器就是用计数的原始实现的 (2…...

2023年海南省职业院校技能大赛(高职组)信息安全管理与评估赛项规程
2023年海南省职业院校技能大赛(高职组) 信息安全管理与评估赛项规程 一、赛项名称 赛项名称:信息安全管理与评估 英文名称:Information Security Management and Evaluation 赛项组别:高等职业教育 赛项归属产业&…...

大模型深挖数据要素价值:算法、算力之后,存储载体价值凸显
文 | 智能相对论 作者 | 叶远风 18.8万亿美元,这是市场预计2030年AI推动智能经济可产生的价值总和,其中大模型带来的AI能力质变无疑成为重要的推动力量。 大模型浪潮下,业界对AI发展的三驾马车——算力、算法、数据任何一个维度的关注都到…...

AI文章,AI文章生成工具
在互联网时代,随着信息爆炸式增长,文章的需求愈发旺盛。从博客、新闻、社交媒体到企业宣传,文字作为传达信息、吸引受众的工具变得愈发重要。但问题是,对于很多人来说,创作一篇高质量的文章并不容易。时间、创意、写作…...
mac有必要用清理软件吗?有哪些免费的清理工具
当我们谈到Mac电脑时,很多人都会觉得它比Windows系统更加稳定和高效,也更不容易积累垃圾文件。但实际上,任何长时间使用的操作系统都会逐渐积累不必要的文件和缓存。那么,对于Mac用户来说,有必要使用专门的清理软件吗&…...
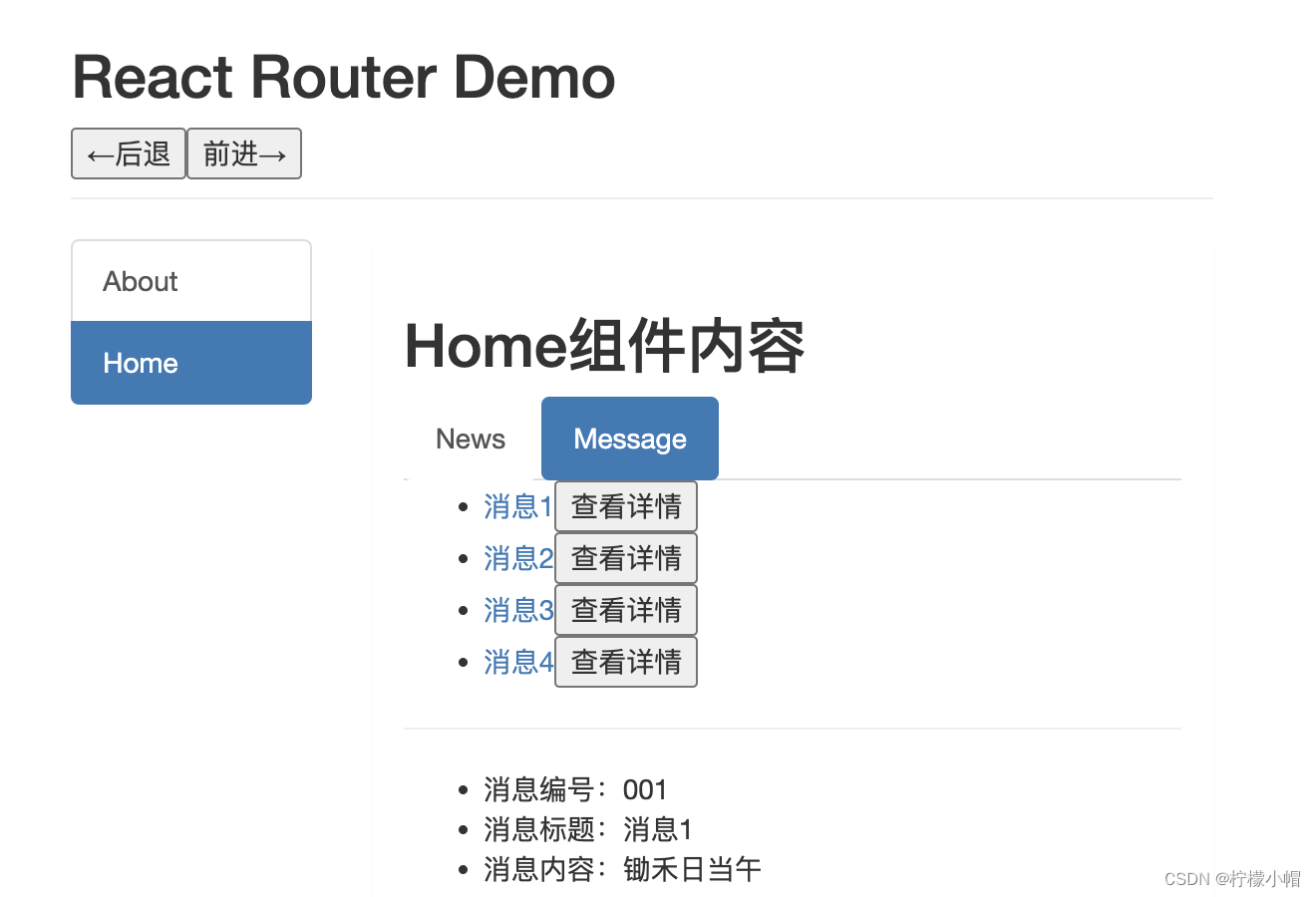
React 全栈体系(十八)
第九章 React Router 6 二、代码实战 6. 路由的 params 参数 6.1 routes /* src/routes/index.js */ import About from "../pages/About"; import Home from "../pages/Home"; import Message from "../pages/Message"; import News from &q…...

TCP/UDP
TCP:可靠的有序传输 TCP是一种面向连接的协议,旨在提供可靠、有序的数据传输。它通过以下方式实现这一目标: 1. 连接建立和维护 在使用TCP传输数据之前,必须先建立连接。这个过程包括三次握手,即客户端和服务器之间…...

c++内存对齐
原文在这里。https://blog.csdn.net/WangErice/article/details/103598081 但是内容有错误。我在自己的这里修改并变成红色了。 内存在使用过程并不是单一的依次排列,而是按照某种既定的规则来进行对齐,以方便快速访问.内存的对齐原则有以下三条&#…...
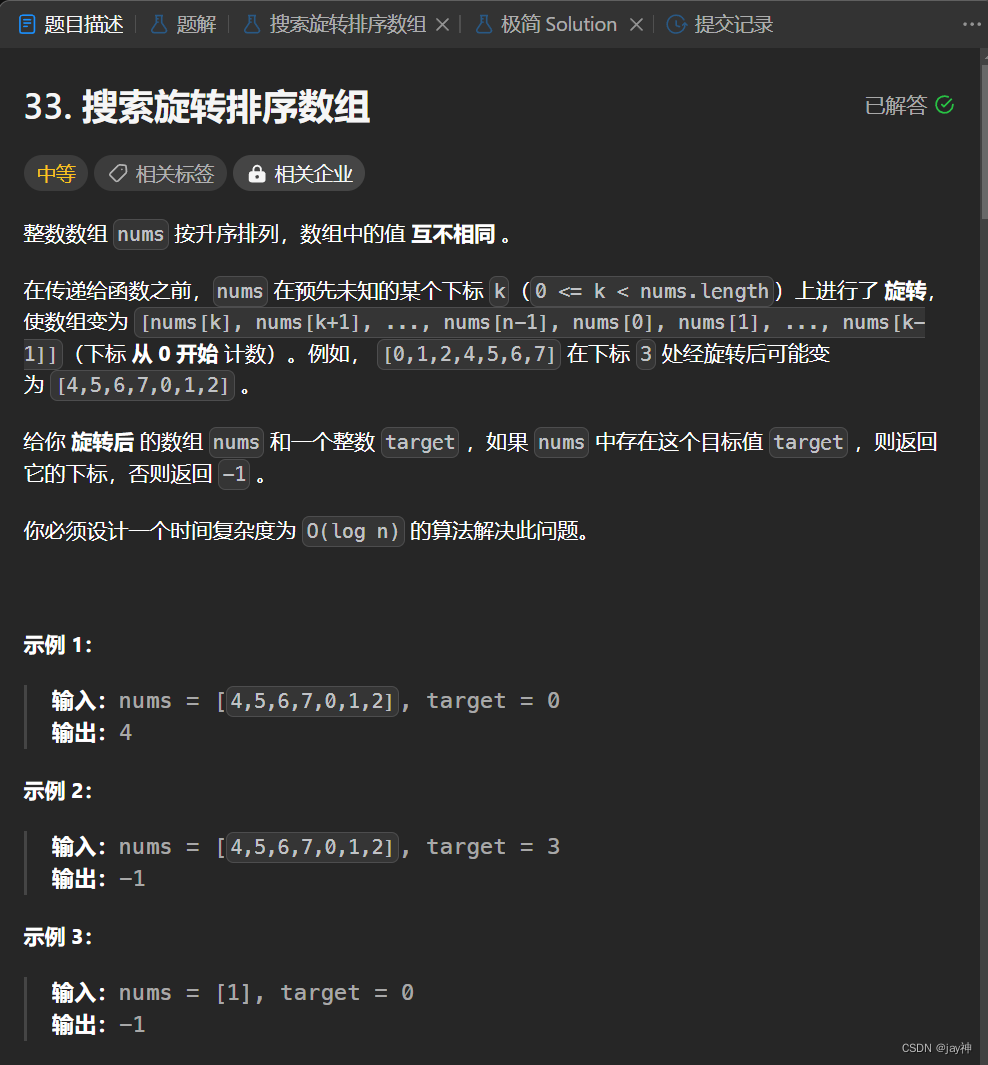
leetcode 33. 搜索旋转排序数组
2023.9.26 本题暴力法可以直接A,但是题目要求用log n的解法。 可以想到二分法,但是一般二分法适用于有序数组的,这里的数组只是部分有序,还能用二分法吗? 答案是可以的。因为数组是经过有序数组旋转得来的,…...

VCS flow学习
VCS VCS 是IC从业者常用软件,该篇文章是一个学习记录,会记录在使用过程中各种概念及options。 VCS Flow VCS Flow 可以分为Two-step Flow和Three-step Flow两类。 两步法 两步法只支持Verilog HDL和SystemVerilog的design,两步法主要包括…...
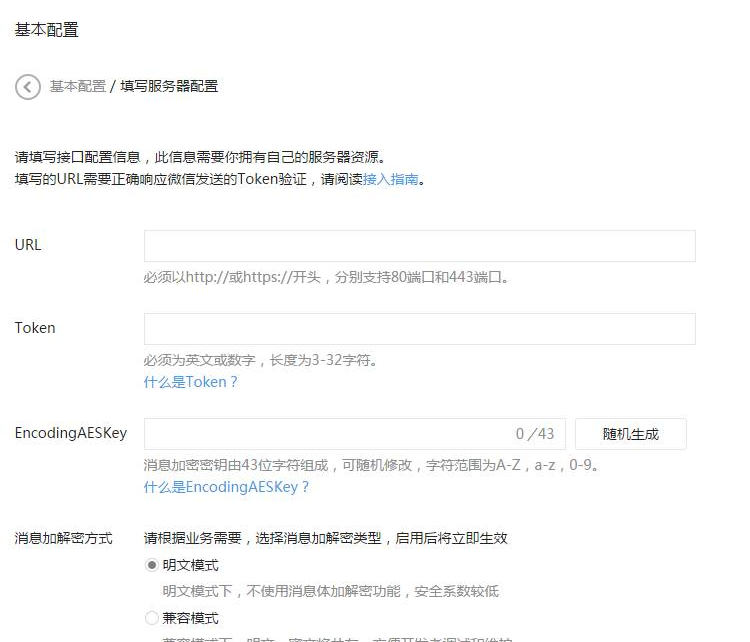
微信扫码关注公众号登录功能php实战分享
1、安装easywechat 基于easywechat框架开发,首先下载安装easywechat composer require overtrue/wechat 2、公众号配置 先去公众号后台基本配置/ 填写服务器配置配置接口,需要是线上能正确收到微信推送消息的地址,关注如果有关注、扫码、收到消息等事件都会推送到该地址…...

Git 精简快速使用
安装 Git 忽略,自行搜索 新建项目,或者在仓库拉取项目,进入到项目目录 Github 给出的引导,新项目和旧项目 echo "# testgit" >> README.md git init git add README.md git commit -m "first commit"…...

线性约束最小方差准则(LCMV)波束形成算法仿真
常规波束形成仅能使得主波束对准目标方向,从而在噪声环境下检测到目标,但无法对复杂多变的干扰做出响应,所以不能称之为真正意义上的自适应滤波。自适应阵列处理指的是采用自适应算法对空间阵列接收的混合信号进行处理,又可称为自…...
什么是内容运营?
关于内容运营,在不同种类的公司,侧重点也不一样。 电商平台的内容运营岗更偏内容营销;产品功能比较简单的公司,内容运营和新媒体运营的岗位职责差不多;而内容平台的内容运营更多的是做内容的管理和资源整合。...

搭建安信可小安派Windows 开发环境
搭建小安派Windows 开发环境 Ai-Pi-Eyes 系列是安信可开源团队专门为Ai-M61-32S设计的开发板,支持WiFi6、BLE5.3。所搭载的Ai-M61-32S 模组具有丰富的外设接口,具体包括 DVP、MJPEG、Dispaly、AudioCodec、USB2.0、SDU、以太网 (EMAC)、SD/MMC(SDH)、SP…...
XML文件反序列化读取
原始XML文件 <?xml version"1.0" encoding"utf-8" ?> <School headmaster"王校长"><Grade grade"12" teacher"张老师"><Student name"小米" age"18"/><Student name&quo…...

会议剪影 | 思腾合力受邀参加2023第二届世界元宇宙大会并作主题演讲
由中国仿真学会、中国指挥与控制学会和北京理工大学共同主办,上海市嘉定区安亭镇人民政府和中国仿真学会元宇宙专业委员会承办的第二届世界元宇宙大会于2023年9月20日-22日在上海安亭举行。 大会以“虚实相生、产业赋能”为主题,聚焦元宇宙关键技术发展的…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...
