博弈论(奇偶考虑法)+计数+DP(判定转dp):CF838C
首先题目有博弈,先分析一波最优策略(步骤:分析性质)。
两个人,所以显然考虑奇偶考虑法+递归考虑。
首先删就是使子问题-1,重新排列是在当前子问题里的。
一个串的排列是有限的,所以这里就可以上奇偶考虑法。如果有偶数种串,则必然是后手先“被迫“进入子问题(要算上初始情况)
考虑假设法:我们可以先假设进入子问题:
- 必赢。先手进!
- 必死。偶串时后手被迫进入,先手胜!
我们的奇偶考虑法证明了串方案wei偶数时先手必胜了!
考虑奇数种时先手能不能赢,同样假设一下:
- 进去必赢。先手胜
- 进去必输。先手被迫进入,后手胜
现在先手就不能再这层耗了,只能进入下一层了。然后结合上面的结论,只能进入子问题种类数是奇数时先手才有机会。
然后好像就卡住了…
然后回到题目看一看,发现问种类数,考虑dp太早了,就先想下计数
假设每种字符出现次数为 a a a,那么就有 a n \frac a n na种串。然后我们现在这个是奇数。
考虑删掉一个变成什么,是 n ! ∏ a ! ( a − 1 ) ! \frac {n!} {\prod a! (a-1)!} ∏a!(a−1)!n!,我们现在希望这个是奇数。我们除一下发现上面要乘个 a n \frac a n na,则这个也要是奇数。
我们考虑我们还漏了什么条件, ∑ a = n \sum a=n ∑a=n。奇偶的话就从二进制的角度推敲一下, n n n 的最低位1必然存在在其中一个 a a a 里,所以 a n \frac a n na 为奇数必然存在。
所以现在只和 n n n 的奇偶有关了。 n n n 偶先手必胜,否则必败。
剩下dp就很简单了。若 n n n 为奇数,我们要构造 a n \frac a n na 为偶数,考虑用全局-奇。
因为有 ∏ a ! ∣ n ! \prod a! | n! ∏a!∣n!,所以 ∏ a ! \prod a! ∏a! 的2的因子和 n ! n! n! 只能相同。考虑类似10,不能用1+1表示,只能用10+0表示。所以每个 a a a 必然是 n n n 的子集。同时 ∑ a = n \sum a=n ∑a=n
然后dp维护下 1 ∏ a ! \frac 1{\prod a!} ∏a!1 的和。
有个小优化,就是钦定当前lowbit必选,最后乘个阶乘即可
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 250010
//#define M
//#define mo
int mo;
int pw(int a, int b) {int ans=1; while(b) {if(b&1) ans*=a; a*=a; b>>=1; ans%=mo; a%=mo; }return ans;
}
int fac[N], inv[N], ifac[N];
void init(int n) {int i; for(i=fac[0]=1; i<=n; ++i) fac[i]=fac[i-1]*i%mo; ifac[n]=pw(fac[n], mo-2); for(i=n-1; i>=0; --i) ifac[i]=ifac[i+1]*(i+1)%mo; for(i=1; i<=n; ++i) inv[i]=ifac[i]*fac[i-1]%mo;
}
int C(int n, int m) {if(m>n) return 0;return fac[n]*ifac[m]%mo*ifac[n-m]%mo;
}
int n, m, i, j, k, T;
int f[27][N], s, t, ans; void Add(int &a, int b) {
// a=(a+b)%mo; a+=b; if(a>=mo || a<=mo) a%=mo;
}int dfs(int i, int s) {
// printf("f[%lld][%lld] %lld\n", i, s, f[i][s]); if(f[i][s]!=-1) return f[i][s]; if(i==0 || s==0) return 0; f[i][s]=0; int j=s&-s, t;
// printf("====\n");
// printf("%lld %lld\n", S, j); for(t=(s-j); ; t=(t-1)&(s-j)) {//ai=tAdd(f[i][s], dfs(i-1, s-j-t)*ifac[t+j]); if(!t) break; }
// printf("f[%lld][%lld]=%lld\n", i, s, f[i][s]); return f[i][s];
}signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
// T=read();
// while(T--) {
//
// }n=read(); k=read(); mo=read(); init(n); if(n%2) return printf("%lld\n", pw(k, n)), 0; memset(f, -1, sizeof(f)); f[0][0]=1;
// for(i=1; i<=k; ++i) printf("%lld %lld %lld\n", fac[n], f[i][0], fac[n]*f[i][0]%mo); for(i=1; i<=k; ++i) {
// printf("dfs[%lld %lld]=%lld\n", i, 0, dfs(i, 0)); Add(ans, fac[n]*dfs(i, n)%mo*C(k, i)%mo*fac[i]%mo); }
// printf("%lld\n", (ans%mo+mo)%mo); Add(ans, pw(k, n)-2*ans); printf("%lld", (ans%mo+mo)%mo); return 0;
}相关文章:
+计数+DP(判定转dp):CF838C)
博弈论(奇偶考虑法)+计数+DP(判定转dp):CF838C
首先题目有博弈,先分析一波最优策略(步骤:分析性质)。 两个人,所以显然考虑奇偶考虑法递归考虑。 首先删就是使子问题-1,重新排列是在当前子问题里的。 一个串的排列是有限的,所以这里就可以…...
郁金香2021年游戏辅助技术中级班(一)
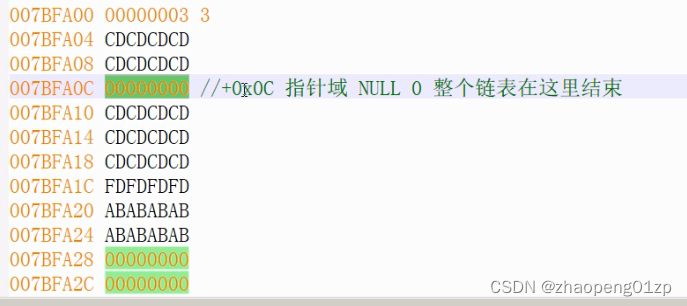
郁金香2021年游戏辅助技术中级班(一) 用代码读取utf8名字字节数组搜索UTF-8字符串 用CE和xdbg分析对象名字从LUA函数的角度进行分析复习怪物名字偏移 用CE和xdbg分析对象数组认识虚函数表分析对象数组 分析对象数组链表部分链表的定义链表的数据在内存里…...
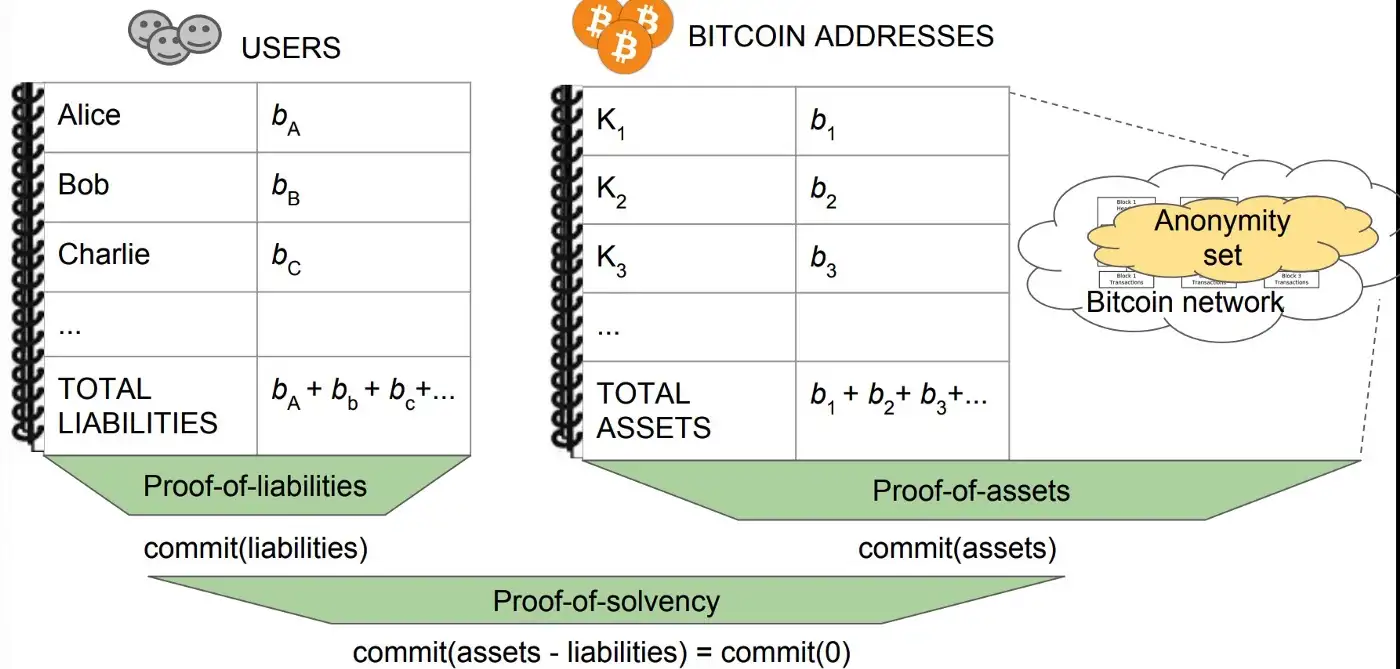
加密货币交易所偿付能力的零知识证明
如何检测下一个 FTX 和 Mt. Gox 加密货币交易所 FTX 的内爆导致数十亿客户资金流失,这是加密货币历史上交易所破产的最新例子。历史可以追溯到 2014 年,当时处理 70% 比特币交易的历史最悠久、规模最大的交易所 Mt. Gox 丢失了用户的 850,000 个比特币。…...

软考网络工程师防火墙配置考点总结
(考试重点) 一、访问控制列表 管理网络当中的数据流量,实现数据过滤的重要手段。可以在路由器、三层交换、二层交换和防火墙上实现。 隐藏规则:当前面的规则都匹配不上,华为默认允许,思科默认拒绝。 分…...
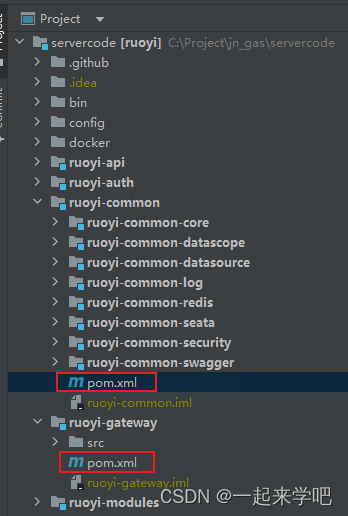
【IDEA】idea恢复pom.xml文件显示灰色并带有删除线
通过idea打开spring boot项目后,发现每个服务中的pom.xml文件显示灰色并带有删除线,下面为解决方案 问题截图 解决方案 打开file——settings——build,execution,deployment——Ignored Files,把pom.xml前面的复选框去掉,去掉之…...

Python数据分析之Excel
Openpyxl库 1、Openpyxl模块2、Excel写入2.1、新建2.2、添加数据2.3、单元格格式 3、Excel读取4、Excel的CRUD4.1、查4.2、改4.3、删 1、Openpyxl模块 Openpyxl是一个用于处理xlsx格式Excel表格文件的第三方python库,几乎支持Excel表格的所有操作 基本概念&#x…...

NISP证书是什么?NISP含金量如何呢?
一、NISP是什么 NISP证书是国家信息安全水平考试(National Information Security Test Program,简称NISP),是由中国信息安全测评中心实施培养国家网络空间安全人才的项目。由国家网络空间安全人才培养基地运营/管理,并…...

操作系统备考学习 day6(2.3.2 - 2.3.4)
操作系统备考学习 day6 第二章 进程与线程2.3 同步与互斥2.3.2 实现临界区互斥的基本方法单标记法双标志先检查法双标志后检查法Peterson算法 进程互斥的硬件实现方法中断屏蔽方法TestAndSet指令Swap指令 2.3.3 互斥锁2.3.4 信号量整型信号量记录型信号量 第二章 进程与线程 2…...

家电行业 EDI:Miele EDI 需求分析
Miele是一家创立于1899年的德国公司,以其卓越的工程技术和不懈的创新精神而闻名于世。作为全球领先的家电制造商,Miele的经营范围覆盖了厨房、洗衣和清洁领域,致力于提供高品质、可持续和智能化的家电产品。公司的使命是为全球消费者创造更美…...
Android ConstraintLayout app:layout_constraintHorizontal_weight
Android ConstraintLayout app:layout_constraintHorizontal_weight <?xml version"1.0" encoding"utf-8"?> <androidx.constraintlayout.widget.ConstraintLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:…...

FPGA行业应用一:LED控制器
什么是LED控制器 LED控制器已经有很多年头了,应该是上世纪90年代就开始有了。它的主要构成是: 1:视频信号源——如 电脑,机机,DVD,U盘等 2:视频处理器——通过 HDMI/DVI/网口接收来自视频源的…...

Pyspark读写csv,txt,json,xlsx,xml,avro等文件
1. Spark读写txt文件 读: df spark.read.text("/home/test/testTxt.txt").show() ------------- | value| ------------- | a,b,c,d| |123,345,789,5| |34,45,90,9878| -------------2. Spark读写csv文件 读: # 文件在hdfs上…...

LeetCode 接雨水 双指针
原题链接: 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题面: 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:…...
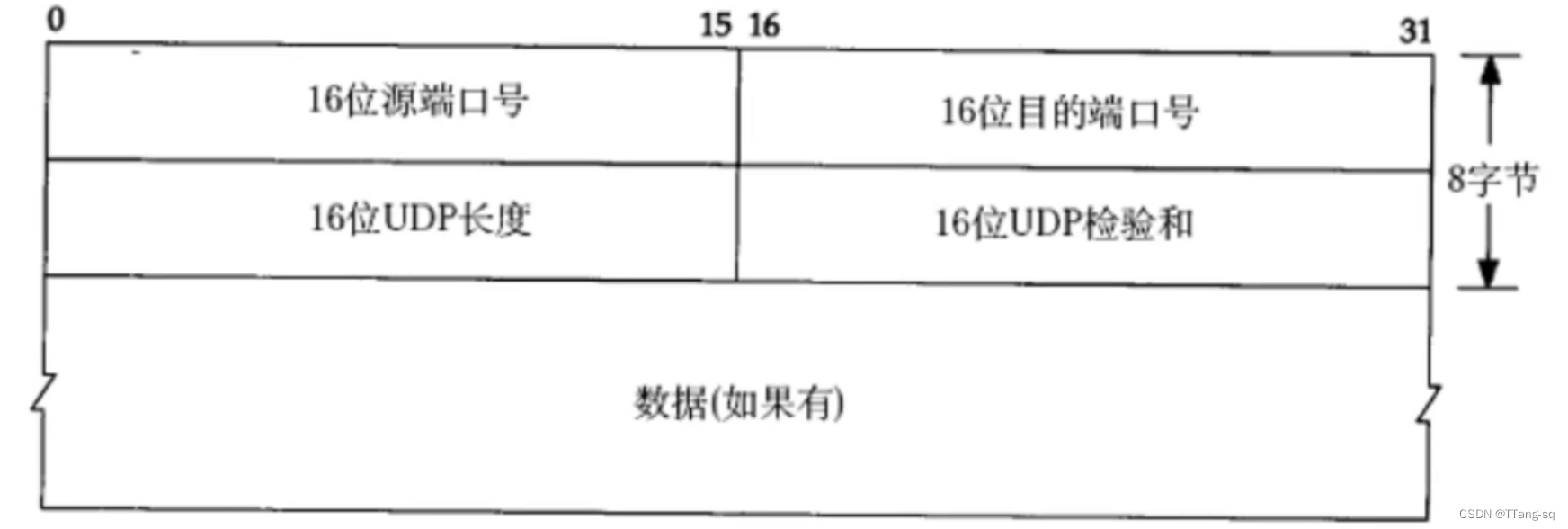
【Linux】【网络】传输层协议:UDP
文章目录 UDP 协议1. 面向数据报2. UDP 协议端格式3. UDP 的封装和解包4. UDP 的缓冲区 UDP 协议 UDP传输的过程类似于寄信。 无连接:知道对端的IP和端口号就直接进行传输,不需要建立连接。不可靠:没有确认机制,没有重传机制&am…...
数字音频工作站FL Studio 21中文版下载及电音编曲要用乐理吗 电音编曲步骤
FL Studio 21是一款强大的数字音频工作站(DAW)软件,为您提供一个完整的软件音乐制作环境。它是制作高质量的音乐、乐器、录音等的完整解决方案。该程序配备了各种工具和插件,帮助你创建专业的虚拟乐器,如贝斯、吉他、钢…...
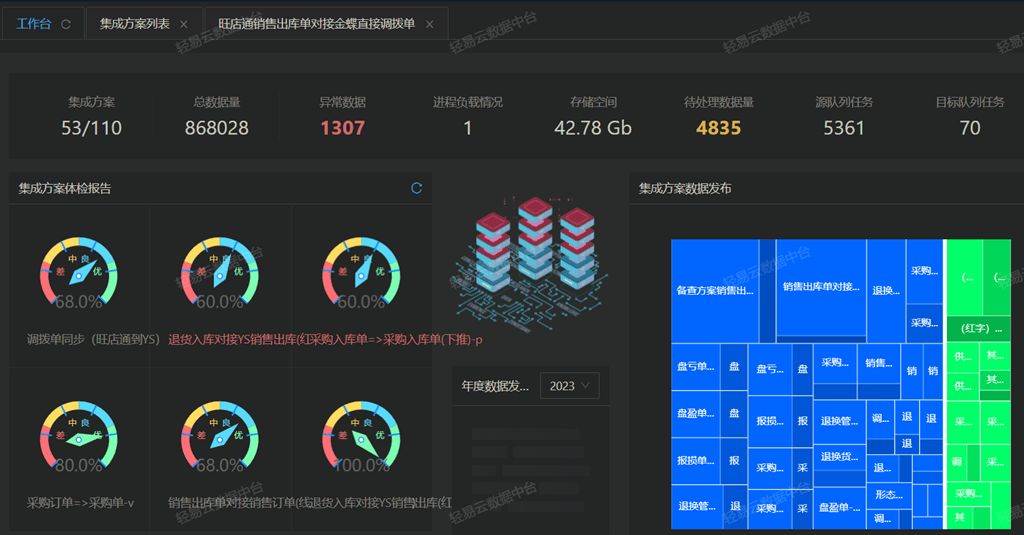
金蝶云星空与旺店通·企业奇门对接集成其他出库查询打通创建其他出库单
金蝶云星空与旺店通企业奇门对接集成其他出库查询打通创建其他出库单 源系统:金蝶云星空 金蝶K/3Cloud(金蝶云星空)是移动互联网时代的新型ERP,是基于WEB2.0与云技术的新时代企业管理服务平台。金蝶K/3Cloud围绕着“生态、人人、体验”&#…...
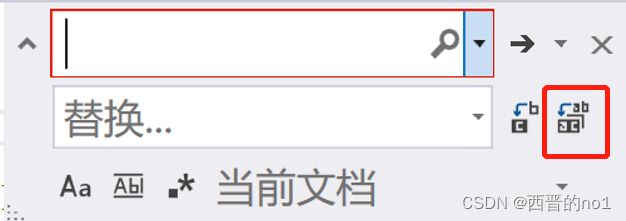
Visual Studio 如何删除多余的空行,仅保留一行空行
1.CtrlH 打开替换窗口(注意选择合适的查找范围) VS2010: VS2017、VS2022: 2.复制下面正则表达式到上面的选择窗口: VS2010: ^(\s*)$\n\n VS2017: ^(\s*)$\n\n VS2022:^(\s*)$\n 3.下面的替换窗口皆写入 \n VS2010: \n VS2017: \n VS2022: \n …...

java spring cloud 企业电子招标采购系统源码:营造全面规范安全的电子招投标环境,促进招投标市场健康可持续发展
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查看所…...
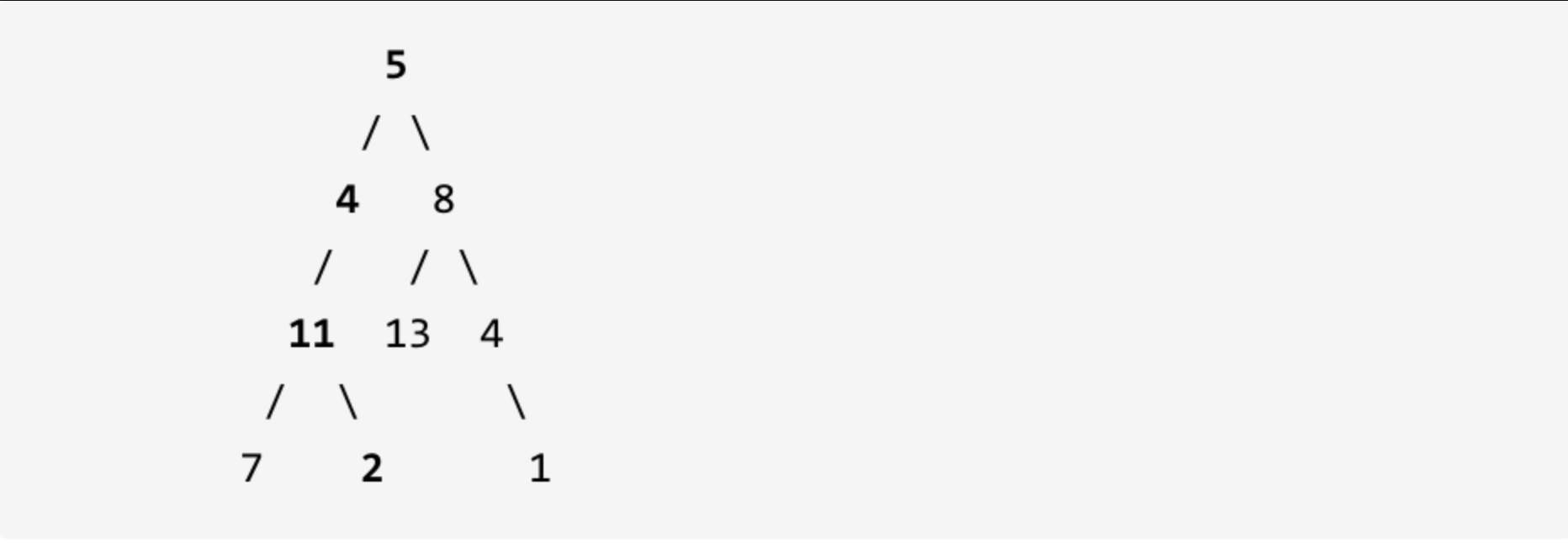
112. 路径总和
力扣题目链接(opens new window) 给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。 说明: 叶子节点是指没有子节点的节点。 示例: 给定如下二叉树,以及目标和 sum 22…...

国货疯抢流量,B站接连爆发800万播放实现破圈
近日,“79元商战”的消息洗刷全平台,众多国货品牌的“不容易”开始被越来越多的消费者注意到,消费者们自发性地开始重新审视真正做产品的国货品牌们,并为之全力支持。有网友笑称:这“泼天的富贵”终于落到了国货品牌的…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...

深入解析 ReentrantLock:原理、公平锁与非公平锁的较量
ReentrantLock 是 Java 中 java.util.concurrent.locks 包下的一个重要类,用于实现线程同步,支持可重入性,并且可以选择公平锁或非公平锁的实现方式。下面将详细介绍 ReentrantLock 的实现原理以及公平锁和非公平锁的区别。 ReentrantLock 实现原理 基本架构 ReentrantLo…...
