stl格式-3D三角形
文章目录
- 什么是stl文件?
- 格式首选
- stl的语法
- 1.这是一个stl格式的文件:
- 2.下面先举个例子(难度略微提示)
- 补充:关于\<\<我试了一下:这个法线你随便写好像也没问题\>>
- 3.来个立方体
- 4.最后再写一个由三个直角形组成的立方体
什么是stl文件?
首先说一下,这个stl不是cpp中的stl库.
指的是以.stl结尾的文件(S T ereo L ithography)
STL(Standard Tessellation Language):STL是一种用于表示三角网格的一种文件格式,它将模型表示为一系列连接的三角形。STL文件通常分为两种类型:ASCII和二进制。ASCII STL文件使用文本表示,包含逐个定义三角面片的数据,而二进制STL文件则使用二进制编码,更紧凑且通常更常用。STL文件广泛用于3D打印和计算机辅助设计(CAD)等领域。
格式首选
STL 文件格式的 ASCII 版本是用纯 ASCII 编写的。但是,由于文件格式较大,因此没有选择该文件格式作为使用的首选格式。
以下从文件大小,读写速度,数据精度,文件解析效率四个方面来解释二进制格式的优势:
- 文件大小:二进制格式的STL文件通常比ASCII格式更小,因为二进制格式使用固定长度的数据表示,而ASCII格式使用可变长度的文本表示。这意味着二进制格式可以更有效地存储模型的几何数据,减少存储和传输的开销。
- 读写速度:由于二进制格式的数据是以二进制编码存储的,相比于ASCII格式,读取和写入二进制STL文件的速度更快。二进制数据可以直接按字节进行读写,无需进行解析和转换操作,因此在处理大型模型或需要频繁读写的场景下,二进制格式能提供更高的效率。
- 数据精度:二进制格式的STL文件可以提供更高的数据精度。由于ASCII格式使用文本表示数字,存在精度损失和舍入误差的问题。而二进制格式使用固定大小的浮点数表示,可以保持更高的精度,并减少舍入误差。
- 文件解析效率:由于二进制格式的STL文件直接存储了几何数据的二进制表示,解析器可以更快速地读取和处理文件。相比之下,解析ASCII格式的STL文件需要进行文本解析和字符串处理,可能会更耗时。
stl的语法
1.这是一个stl格式的文件:
solid namefacet normal ni nj nkouter loopvertex v1x v1y v1zvertex v2x v2y v2zvertex v3x v3y v3zendloopendfacet
endsolid name
聪明的小伙伴应该意识到了:
ni nj nk
与
v1x v1y v1z
v2x v2y v2z
v3x v3y v3z
就是我们要填入的参数
{
ni nj nk代表法线的方向
v1x v1y v1z是顶点1的坐标,
然后是顶点2,顶点3的坐标然后法线(高一知识终于用到了,然后考研也考)的方向可以通过计算三个顶点的叉乘得到.[这是一种方法(还有就是,如果你不会求法线也不要怕,后面写的很详细)]或者是你已经有了一个具体的模型,然后你可以使用Blender软件来获取相关数据[这是第二种方法,在这篇文章,咱们仅仅只谈方法一,因为方法二是使用轮子,方法一是造轮子,现在咱们来沉下心来造轮子!]
}然后name想填啥就填啥,只要保证solid name与endsolid name保持一致就OK了!!!
2.下面先举个例子(难度略微提示)
(其实难度也不是很高,难度在于:网上还没有中文资料,大多数都是英文的,然后即使翻译过来,如果不是专业的翻译人员,翻译过来的意思也不是那么通俗易懂)
现在假设有一个平面三角形,顶点坐标为:
顶点一:(0,0,0)
顶点二:(1,0,0)
顶点三:(0,1,0)
(这个也很简单,大家可以在纸上画一下)
然后我们就要填入数据了!首先,计算就是计算法线的方向.法线的方向可以通过计算任意两条边的叉积得到.
我们计算顶点2和顶点1以及顶点3与顶点1的向量:
向量a = (1,0,0)-(0,0,0) = (1,0,0) = (a₁,a₂,a₃)
向量b = (0,1,0)-(0,0,0) = (0,1,0) = (b₁,b₂,b₃)法线的方向就直接axb得到:ni nj nk = axb = (0,0,1)
然后,至于为啥 (1,0,0) X X X (0,1,0) = (0,0,1)?
根据叉积的计算公式为:23 32, 31 13,12 21
a × b a × b a×b = ( a ₂ b ₃ a₂b₃ a₂b₃- a ₃ b ₂ a₃b₂ a₃b₂, a ₃ b ₁ a₃b₁ a₃b₁ - a ₁ b ₃ a₁b₃ a₁b₃, a ₁ b ₂ a₁b₂ a₁b₂ - a ₂ b ₁ a₂b₁ a₂b₁)
=(0x0-0x1, 0x0-1x0, 1x1-0x0)
=(0, 0 ,1)
(然后,再强调一下,叉积和矩阵相乘是两回事!!!)
至于三维的叉积公式怎么记?可以看下图:记住23 31 自然就记住了全部了
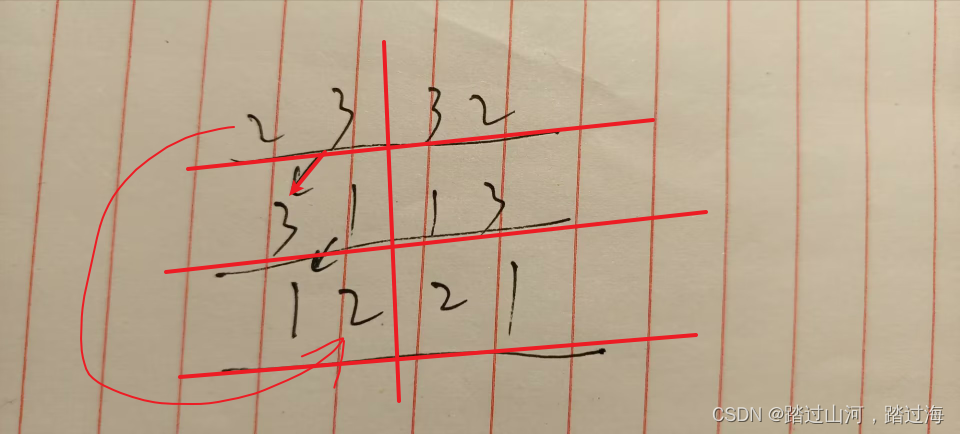
因此,法线就是(0,0,1)
所以,我们完成的stl文件格式如下:solid testfacet normal 0 0 1 //我试了一下:这个法线你随便写好像也没问题outer loopvertx 0 0 0vertx 1 0 0vertx 0 1 0endloopendfacet
endsolid test
补充:关于<<我试了一下:这个法线你随便写好像也没问题>>
法线你随便写,确实还是可以正常显示stl的3d图像的,但是颜色好像变深或者变浅了
这就是涉及到法线的作用了:
STL文件中的法线向量是用于确定三角面片的朝向和光照效果的。法线向量指示了面片的表面方向,使软件能够确定如何着色和渲染模型。
当你随意更改法线向量时,STL文件仍然可以显示出来,但视觉效果可能会发生变化。由于法线向量的改变,渲染引擎可能会根据新的法线方向重新计算面片的光照效果,导致颜色变深或变浅。
然而,这种方式并不代表结果是正确的或符合实际形状的。正确的法线方向对于准确显示和渲染三维模型非常重要。如果法线方向错误或不一致,可能会导致不自然的阴影、光照效果不良或渲染问题。
因此,为了正确呈现和渲染模型,请确保为每个面片定义正确的法线方向,并确保它们与实际表面法线方向相匹配。这样可以确保模型在渲染时获得更准确的外观和光照效果。
3.来个立方体
其实一组这个,就代表一个立方体facet normal ni nj nkouter loopvertex v1x v1y v1zvertex v2x v2y v2zvertex v3x v3y v3zendloop
endfacet然后一个正方形需要两组,所以就是十二组
solid testfacet normal 0 0 1outer loopvertex 0 0 0vertex 1 0 0vertex 0 1 0endloopendfacetfacet normal 0 0 1outer loopvertex 1 1 0vertex 0 1 0vertex 1 0 0endloopendfacetfacet normal 0 0 -1outer loopvertex 0 0 1vertex 0 1 1vertex 1 0 1endloopendfacetfacet normal 0 0 -1outer loopvertex 1 1 1vertex 1 0 1vertex 0 1 1endloopendfacetfacet normal 0 1 0outer loopvertex 0 1 0vertex 1 1 1vertex 0 1 1endloopendfacetfacet normal 0 1 0outer loopvertex 1 1 0vertex 0 1 0vertex 1 1 1endloopendfacetfacet normal 0 -1 0outer loopvertex 0 0 0vertex 0 0 1vertex 1 0 0endloopendfacetfacet normal 0 -1 0outer loopvertex 1 0 1vertex 1 0 0vertex 0 0 1endloopendfacetfacet normal 1 0 0outer loopvertex 1 0 0vertex 1 1 1vertex 1 0 1endloopendfacetfacet normal 1 0 0outer loopvertex 1 1 0vertex 1 0 0vertex 1 1 1endloopendfacetfacet normal -1 0 0outer loopvertex 0 0 0vertex 0 1 0vertex 0 0 1endloopendfacetfacet normal -1 0 0outer loopvertex 0 1 1vertex 0 0 1vertex 0 1 0endloopendfacet
endsolid test
4.最后再写一个由三个直角形组成的立方体
solid Cylinderfacet normal 0.0 1.0 0.0outer loopvertex 0.0 0.0 0.0vertex 0.0 0.0 1.0vertex 1.0 0.0 0.0endloopendfacet facet normal 0.0 0.0 1.0outer loopvertex 0.0 0.0 0.0vertex 1.0 0.0 0.0vertex 0.0 1.0 0.0endloopendfacetfacet normal 0.0 0.0 1.0outer loopvertex 0.0 0.0 0.0vertex 0.0 1.0 0.0vertex 0.0 0.0 1.0endloopendfacetfacet normal 1.0 0.0 0.0outer loopvertex 0.0 0.0 1.0vertex 1.0 0.0 0.0vertex 0.0 1.0 0.0endloopendfacetendsolid Cylinder
相关文章:

stl格式-3D三角形
文章目录 什么是stl文件?格式首选stl的语法1.这是一个stl格式的文件:2.下面先举个例子(难度略微提示)补充:关于\<\<我试了一下:这个法线你随便写好像也没问题\>> 3.来个立方体4.最后再写一个由三个直角形组成的立方体 什么是stl文件? 首先说一下,这个stl不是cpp…...

基于微信小程序的高校暑期社会实践小程序设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言系统主要功能:具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计…...

ARM-day2
1、 .text .global _start_start:MOV r0, #0x1ADDS r1,r0, #0x1cmp r1, #100bl funstop:b stopfun:ADD r2,r1,r1.end2、思维导图...
macOS Sonoma 14 正式版(23A344)发布,附黑/白苹果镜像下载地址
系统介绍(系统下载地址:http://www.imacosx.cn/115300.html) 黑果魏叔9 月 27日消息,苹果今日向 Mac 电脑用户推送了 macOS Sonoma 14 正式版(23A344)。 macOS 14正式版系统发布:全新功能与改…...

HarmonyOS开发:封装一个便捷的Log工具类
前言 日志打印,没什么好说的,系统已给我们提供,且调用也是非常的简单,我们封装的目的,一是扩展,打印一些不常见的类型,比如格式化json,使得日志看起来比较好看,二是&…...
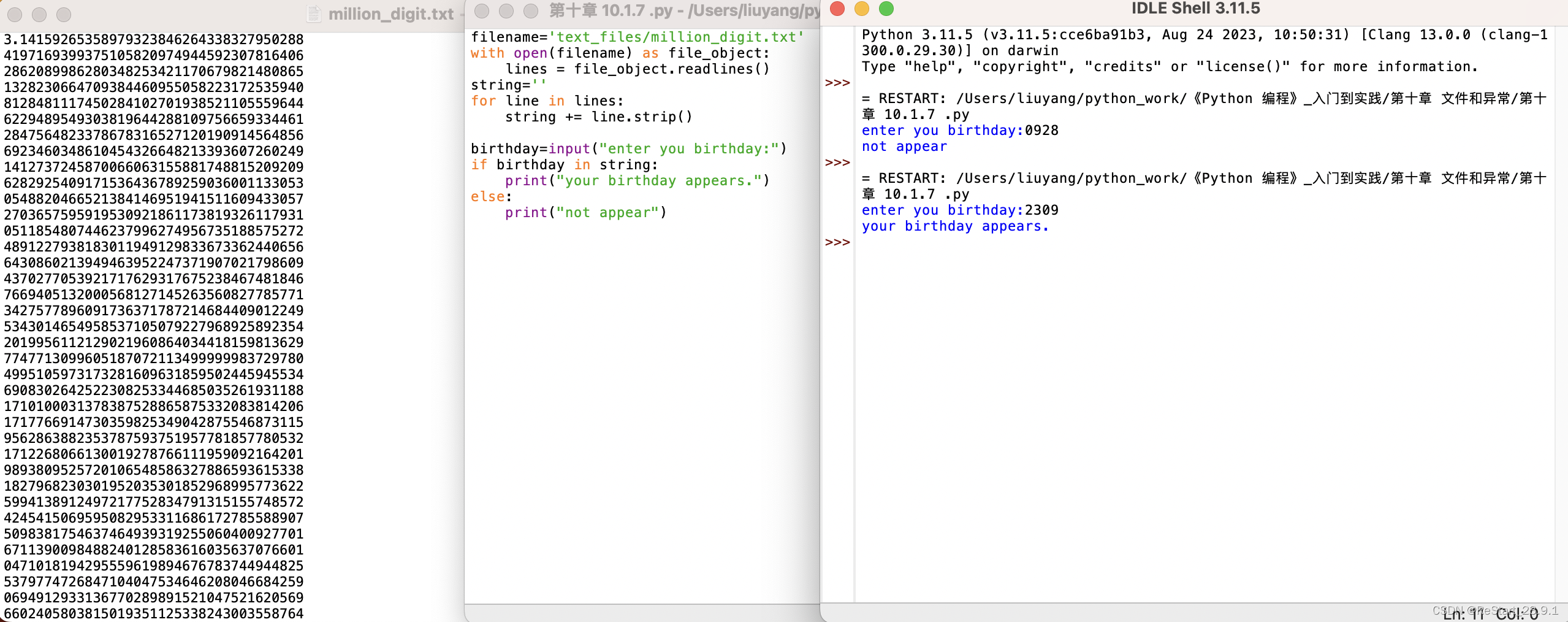
第十章_祖冲之_圆周率
倒数1又2/3章,keep_writting的一天: 第十章10.1.7 运行程序资源下载网站为何打不开呢?...

FVM管理Flutter 环境
开发中,会经常切换不同版本的 Flutter 环境。使用 FVM(Flutter Version Manager )来进行 Flutter 版本切换是一个很不错的选择。 下面从安装FVM、环境配置、切换Flutter这几个主要步骤总结下 FVM 的使用 一、安装 homebrew 网址࿱…...
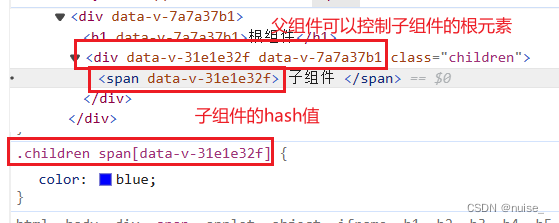
vue | 样式隔离scoped的原理 样式穿透deep的原理
文章目录 vue中的样式穿透scoped 样式隔离父组件可以修改子组件根节点样式 deep 样式穿透:deep(.el-col)的原理 vue中的样式穿透 scoped 样式隔离 一个style标签拥有scoped属性时,css样式就只能作用于当前的组件,这样就可以使得组件之间的样式不互相污…...

UML,集合框架
1.什么是UML UML是统一建模语言的简称,它是一种由一整套图表组成的标准化建模语言。UML用于帮助系统开发人员阐明,展示,构建和记录软件系统的产出。UML代表了一系列在大型而复杂系统建模中被证明是成功的做法,是开发面向对象软件…...
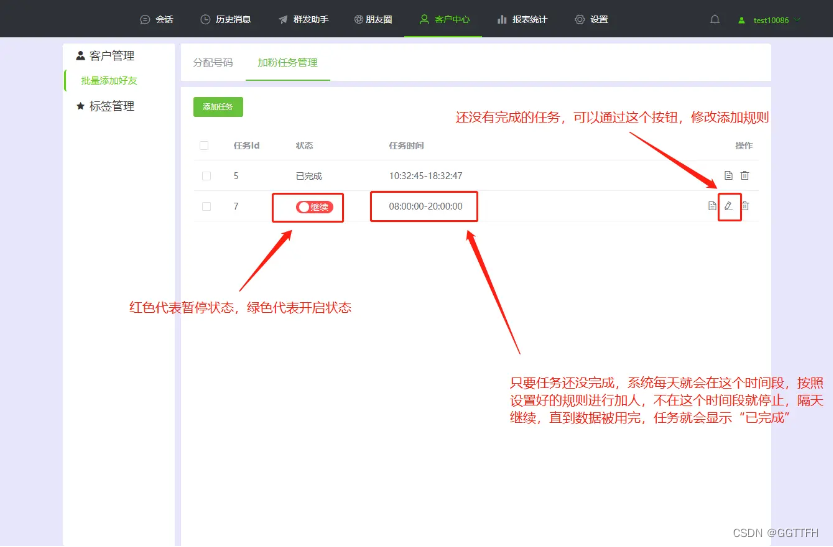
如何快速轻松自动添加微信好友?
有些客需要换新的微信号,想把以前微信号上的好友全部加回来,但是因为微信系统的规定,频繁加好友容易被封号,而且手动添加好友太费时费力,还要控制加好友的间隔时间。那么有没有什么方法可以快速轻松自动添加好友呢&…...

MySQL高级语句(第一部分)
MySQL高级语句(第一部分)一、MySQL进阶查询1、select ----显示表格中一个或数个字段的所有数据记录2、distinct ----不显示重复的数据记录3、where ----有条件查询4、and or ----且 或5、in ----显示已知的值的数据记录6、between ----显示两个值范围内的数据记录7、通配符8、l…...

Perl区分文件换行符类型
背景 在Windows上使用Perl判断文件时何种换行符时,处理CR LF类型的换行符时,也识别成了LF。 思路 Windows上的换行是 CRLF , Unix上是 LF , Mac CR在Windows平台使用Perl读取文件创建文件句柄时,未对file handler设置binmode,了…...
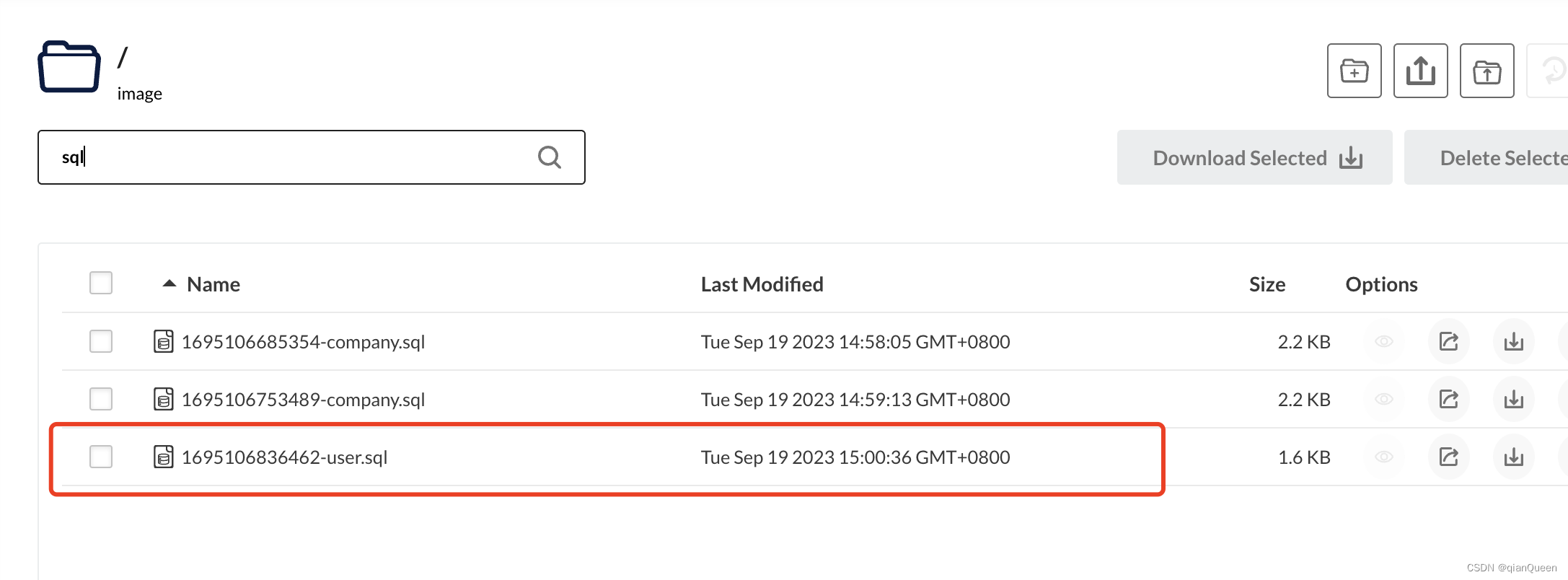
数据备份文件生成--根据表名生成对应的sql语句文件
最近客户有个需求,希望在后台增加手动备份功能,将数据导出下载保存。 当然,此方法不适用于海量数据的备份,这只适用于少量数据的sql备份。 这是我生成的sql文件,以及sql文件里的insert语句,已亲测&#x…...

进程同步与互斥
目录 进程同步与互斥(1) 第一节、进程间相互作用 一、相关进程和无关进程 二、与时间有关的错误 第二节、进程同步与互斥 一、进程的同步 二、进程的互斥 三、临界区 进程同步与互斥(2) 三、信号量与P、V操作的物理含义…...
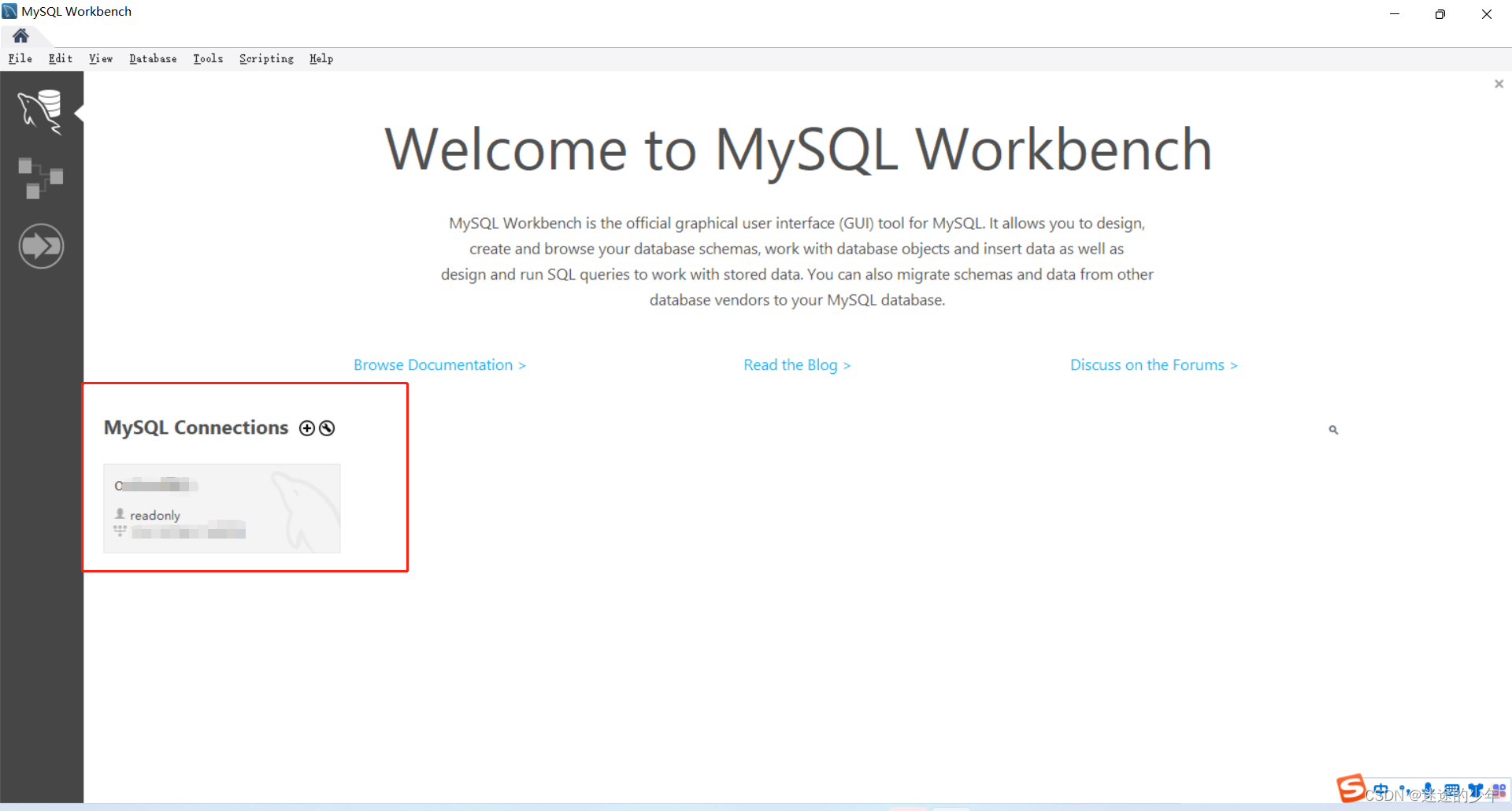
mysql workbench常用操作
1、No database selected Select the default DB to be used by double-clicking its name in the SCHEMAS list in the sidebar 方法一:双击你要使用的库 方法二:USE 数据库名 2、复制表名,字段名 3、保存链接...

【操作】国标GB28181视频监控EasyGBS平台更新设备信息时间间隔
国标GB28181协议视频平台EasyGBS是基于GB28181协议的视频监控云服务平台,可支持多路设备同时接入,并对多平台、多终端分发出RTSP、RTMP、FLV、HLS、WebRTC等格式的视频流。平台可提供视频监控直播、云端录像、云存储、检索回放、智能告警、语音对讲、平台…...
TensorFlow入门(八、TensorBoard可视化工具的应用)
TensorBoard常用函数和类http://t.csdn.cn/Hqi9c TensorBoard可视化的过程: ①确定一个整体的图表,明确从这个图表中获取哪些数据的信息 ②确定在程序的哪些节点、以什么样的方式进行汇总数据的运算,以记录信息,比如在反向传播定义以后,使用tf.summary.scalar记录损失值的变…...
)
升级targetSdkVersion至33(以及迁移至Androidx)
1.设置 android.useAndroidXtrue 和 android.enableJetifiertrue 2.一键迁移至androidx:Refactor -> Migrate to Androidx 3.手动修改未能自动迁移到androidx的部分: android.support.v4.view.ViewPager.PageTransformer -> androidx.viewpager.wi…...

python3.11版本pip install ddddocr调用时报错got an unexpected keyword argument ‘det‘ 解决
一、如图出现如下问题 ddddocr.__init__() got an unexpected keyword argument det出现问题原因:python3.11默认安装版本就旧版的ddddocr1.0的,所以导致如下报错 二、解决方案一(推荐) python3.11的环境直接安装这个即可&…...

代理IP与Socks5代理:跨界电商之安全防护与智能数据引擎
第一部分:跨界电商的兴起与网络安全挑战 1.1 跨界电商的崭露头角 跨界电商已经成为全球贸易的新引擎,企业纷纷踏上了拓展国际市场的征程。 1.2 网络安全的不容忽视 跨界电商的增长也伴随着网络安全威胁的增加。黑客攻击、数据泄露和欺诈行为等风险呈…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
