Leetcode.2571 将整数减少到零需要的最少操作数
题目链接
Leetcode.2571 将整数减少到零需要的最少操作数
rating : 1649
题目描述
给你一个正整数 n n n ,你可以执行下述操作 任意 次:
- n n n 加上或减去 2 2 2 的某个 幂
返回使 n n n 等于 0 0 0 需要执行的 最少 操作数。
如果 x = 2 i x = 2^i x=2i 且其中 i ≥ 0 i \geq 0 i≥0 ,则数字 x x x 是 2 2 2 的幂。
示例 1:
输入:n = 39
输出:3
解释:我们可以执行下述操作:
- n 加上 20 = 1 ,得到 n = 40 。
- n 减去 23 = 8 ,得到 n = 32 。
- n 减去 25 = 32 ,得到 n = 0 。
可以证明使 n 等于 0 需要执行的最少操作数是 3 。
示例 2:
输入:n = 54
输出:3
解释:我们可以执行下述操作:
- n 加上 21 = 2 ,得到 n = 56 。
- n 加上 23 = 8 ,得到 n = 64 。
- n 减去 26 = 64 ,得到 n = 0 。
使 n 等于 0 需要执行的最少操作数是 3 。
提示:
- 1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105
解法:贪心
我们用 c n t cnt cnt 表示连续的 1 1 1 的个数 , a n s ans ans 表示操作数。
此时遇到的是 0 0 0:
- 如果此时 c n t = 1 cnt = 1 cnt=1,那么此时直接选择减去这个 1 1 1 即可,即 a n s = a n s + 1 ans = ans + 1 ans=ans+1, c n t = 0 cnt = 0 cnt=0;
- 如果此时 c n t > 1 cnt > 1 cnt>1,那么此时有多个连续的 1 1 1,所以我们选择相加,将这多个 1 1 1 变为 1 个 1 1 1,即 a n s = a n s + 1 ans = ans + 1 ans=ans+1, c n t = 1 cnt = 1 cnt=1;
最后如果 c n t = 1 cnt = 1 cnt=1,说明还有一个 1 1 1 ,直接减去即可,即 a n s = a n s + 1 ans = ans + 1 ans=ans+1;
如果 c n t > 1 cnt > 1 cnt>1,说明最后还有多个连续的 1 1 1,我们需要用两步将其减为 0 0 0,即 a n s = a n s + 2 ans = ans + 2 ans=ans+2。
时间复杂度: O ( l o g n ) O(logn) O(logn)
C++代码:
class Solution {
public:int minOperations(int n) {int ans = 0 , cnt = 0;while(n){if(n & 1) cnt++;else{if(cnt == 1) ans++ , cnt = 0;else if(cnt > 1) ans++ , cnt = 1;}n >>= 1;}if(cnt == 1) ans++;else if(cnt > 1) ans += 2;return ans;}
};
相关文章:

Leetcode.2571 将整数减少到零需要的最少操作数
题目链接 Leetcode.2571 将整数减少到零需要的最少操作数 rating : 1649 题目描述 给你一个正整数 n n n ,你可以执行下述操作 任意 次: n n n 加上或减去 2 2 2 的某个 幂 返回使 n n n 等于 0 0 0 需要执行的 最少 操作数。 如果 x 2 i x 2^…...
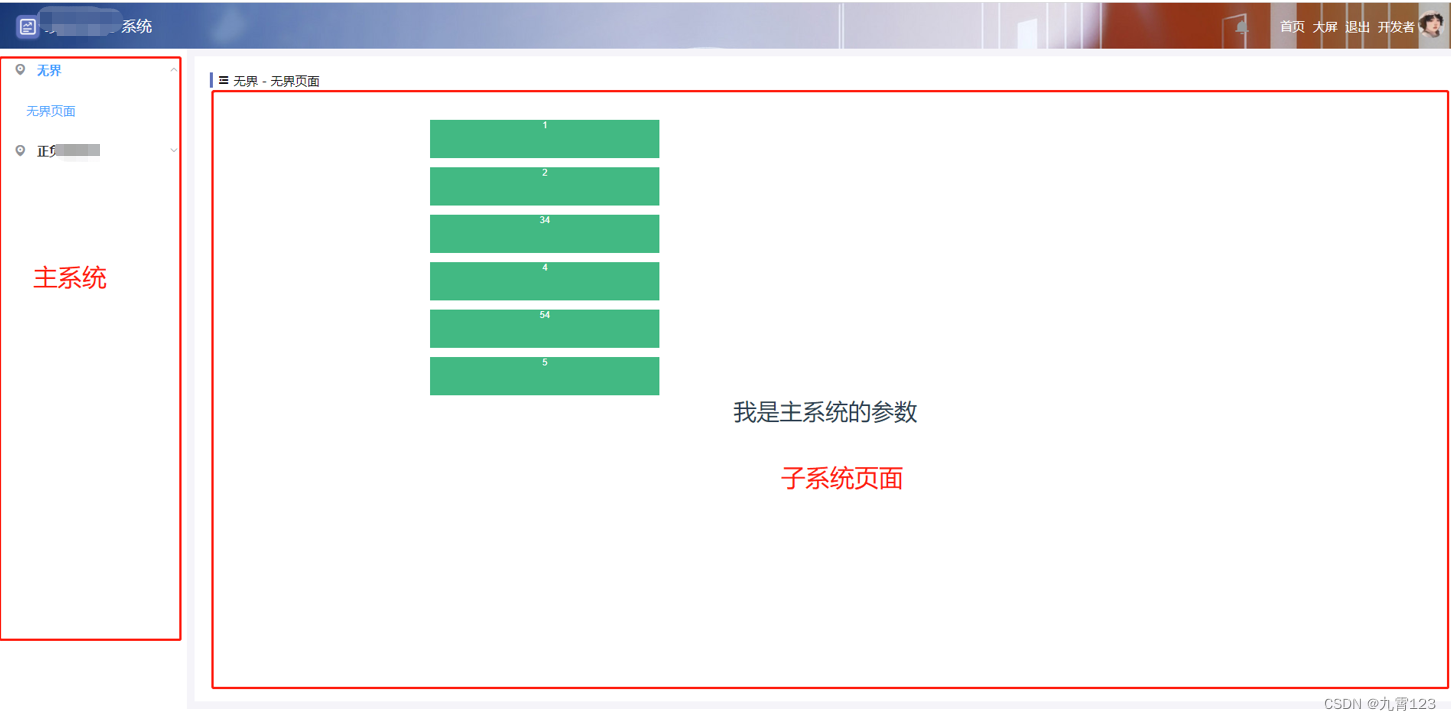
微前端无界 项目使用记录
1预期目标和场景 一个vue框架开发的应用,需要使用另一个系统的页面。 通俗来说,就是在一个web应用中独立的运行另一个web应用 2 技术支持 微前端处理方案:无界 无界官网: https://wujie-micro.github.io/doc/guide/ CSDN 参考…...

CDH 6.3.2升级Flink到1.17.1版本
CDH:6.3.2 原来的Flink:1.12 要升级的Flink:1.17.1 操作系统:CentOS Linux 7 一、Flink1.17编译 build.sh文件: #!/bin/bash set -x set -e set -vFLINK_URLsed /^FLINK_URL/!d;s/.*// flink-parcel.properties FLI…...
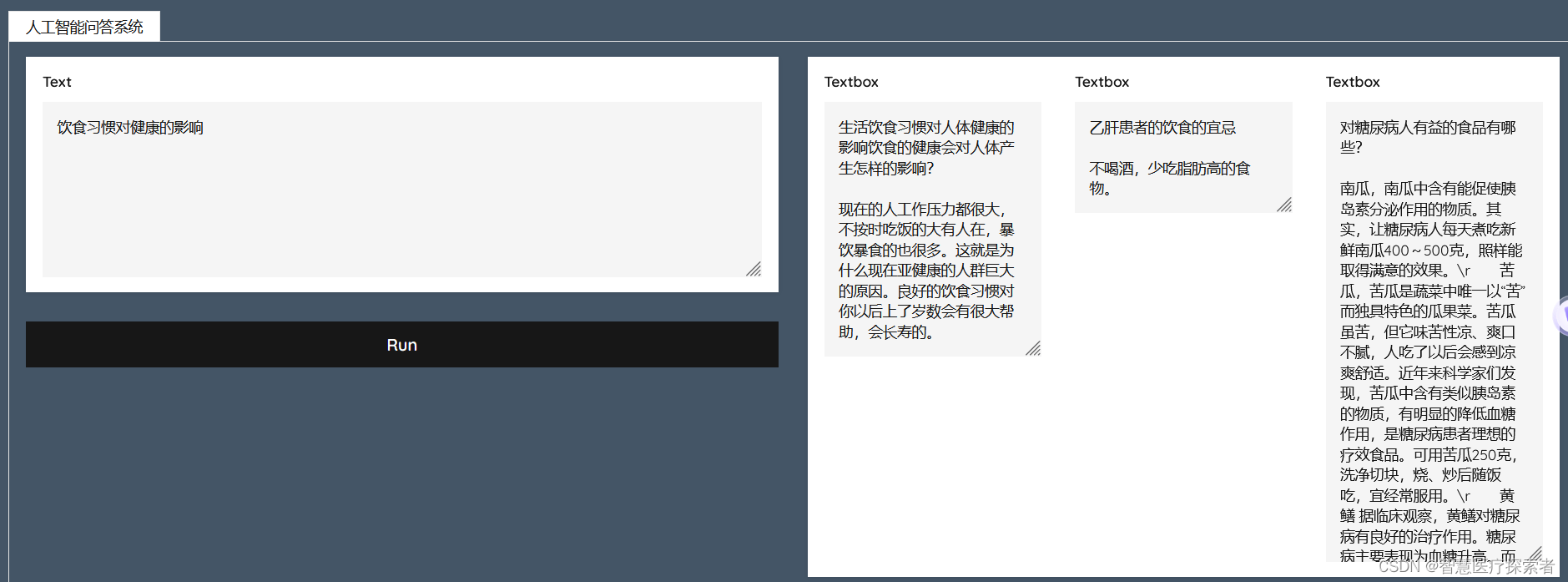
基于谷歌Transeformer构建人工智能问答系统
目录 1 项目背景 2 关键技术 2.1 Transeformer模型 2.2 Milvus向量数据库 3 系统代码实现 3.1 运行环境构建 3.2 数据集介绍 3.3 预训练模型下载 3.4 代码实现 3.4.1 创建向量表和索引 3.4.2 构建向量编码模型 3.4.3 数据向量化与加载 3.4.4 构建检索web 3.5 运行结…...
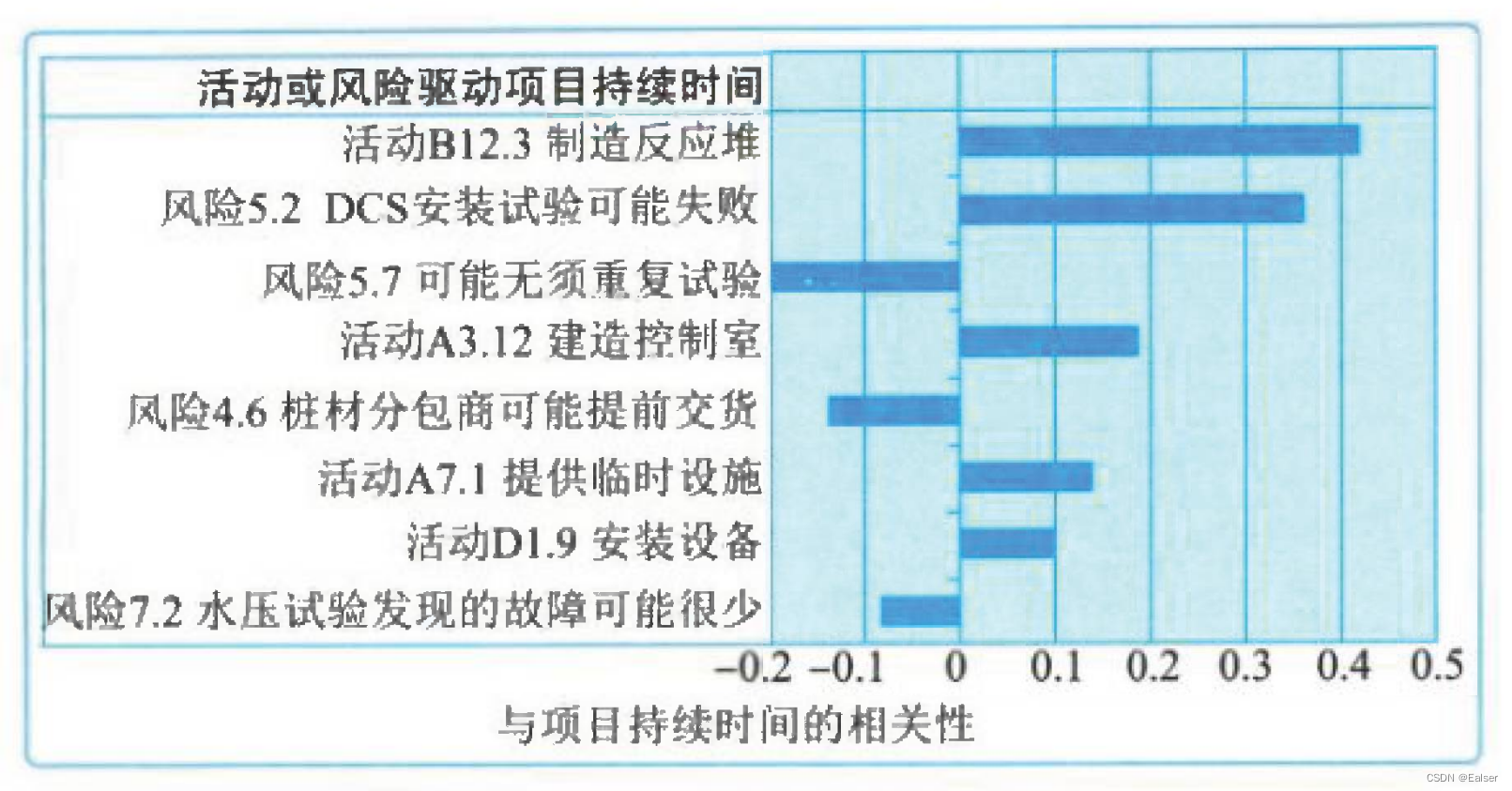
【2023年11月第四版教材】第15章《风险管理》(合集篇)
第15章《风险管理》(合集篇) 1 章节说明2 管理基础2.1 风险的属性2.2 风险的分类★★★2.3 风险成本★★★2.4 管理新实践 3 管理过程4 管理ITTO汇总★★★5 过程1-规划风险管理6 过程2-识别风险6.1 识别风险★★★6.2 数据收集★★★6.3 数据分析★★★…...

python常见面试题四
解释 Python 中的魔术方法 (magic methods)。 答:魔术方法是以双下划线 __ 开头和结尾的方法,用于在特定条件下自动调用。例如,__init__ 是用于初始化对象的魔术方法。 解释 Python 中的装饰器 (decorator)。 答:装饰器是一种特殊…...
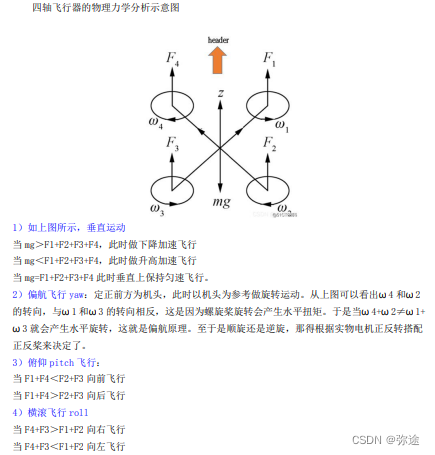
stm32无人机-飞行力学原理
惯性导航,是一种无源导航,不需要向外部辐射或接收信号源,就能自主进行确定自己在什么地方的一种导航方法。 惯性导航主要由惯性器件计算实现,惯性器件包括陀螺仪和加速度计。一般来说,惯性器件与导航物体固连…...
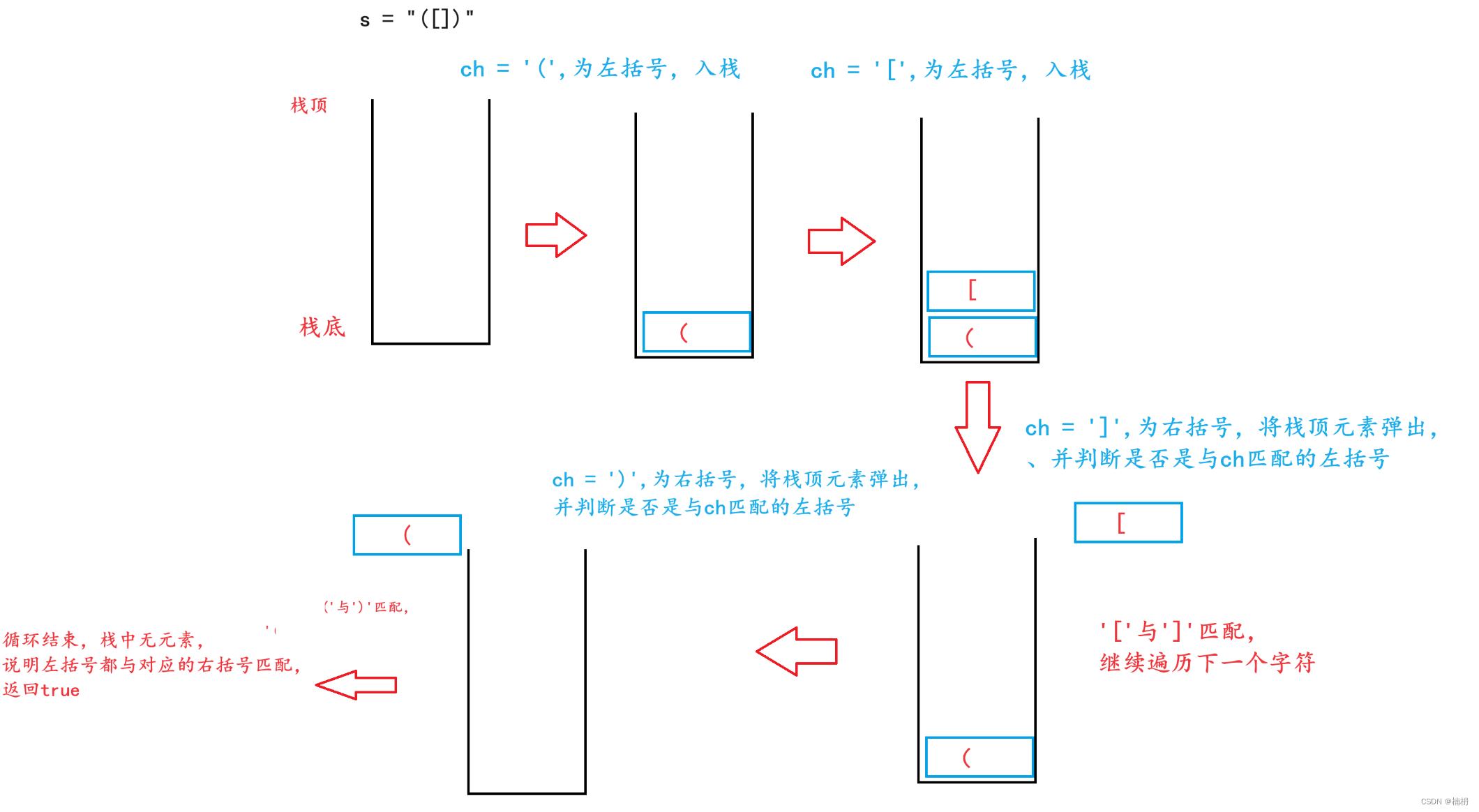
Java括号匹配
目录 一、题目描述 二、题解 一、题目描述 给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭…...

自动化测试-友好的第三方库
目录 mock furl coverage deepdiff pandas jsonpath 自动化测试脚本开发中,总是会遇到各种数据处理,例如MOCK、URL处理、JSON数据处理、结果断言等,也会遇到所采用的测试框架不能满足当前需求,这些问题都需要我们自己动手解…...

基于微信小程序的火锅店点餐订餐系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言系统主要功能:具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计…...
亿图脑图新版本支持思维导图一键生成PPT、音视频等格式,办公提效再升级
近日,国产思维导图软件——亿图脑图MindMaster发布了全新版本V10.9.0,本次亿图脑图的升级给用户带来了极大的惊喜。全新升级的亿图脑图MindMaster不仅支持20格式的文件智能解析成思维导图,还支持思维导图一键生成PPT、音频、视频等内容形式&a…...
Arthas:Java调试利器使用
Arthas:Java调试利器使用 1. Arthas是什么2. Arthas可以解决什么问题Arthas启动方式1. jar启动2. 在线安装 远程连接命令使用- 退出threadclassloaderscsm watchtrace修改日志级别 1. Arthas是什么 Arthas(阿尔萨斯)是阿里开源的一个Java在线分析诊断工具. 2. Arthas可以解决…...

Nuxt 菜鸟入门学习笔记七:SEO 和 Meta 设置
文章目录 SEO 和 Meta默认值useHeaduseSeoMeta 和 useServerSeoMetaComponentsMeta 对象数据类型格式特性响应式 Reactivity标题模板 Title TemplateBody Tags 示例 ExamplesdefinePageMeta动态设置标题动态添加外部 CSS Nuxt 官网地址: https://nuxt.com/ SEO 和 …...

栈(Stack)和队列(Queue)
栈(Stack)和队列(Queue)都是常见的数据结构,用于存储和操作一组元素。 栈是一种后进先出(Last-In-First-Out,LIFO)的数据结构,类似于把元素堆在一起形成的一堆物体&…...

LeetCode 75 part 06 栈
2390.从字符串中移除星号 思路:把元素加入栈中,遇到 * 号直接弹出栈顶元素 class Solution { public:string removeStars(string s) {stack<char>st;for(int i0;i<s.size();i){//字符加入栈,遇到星号弹出栈if(s[i]!*) st.push(s[i…...
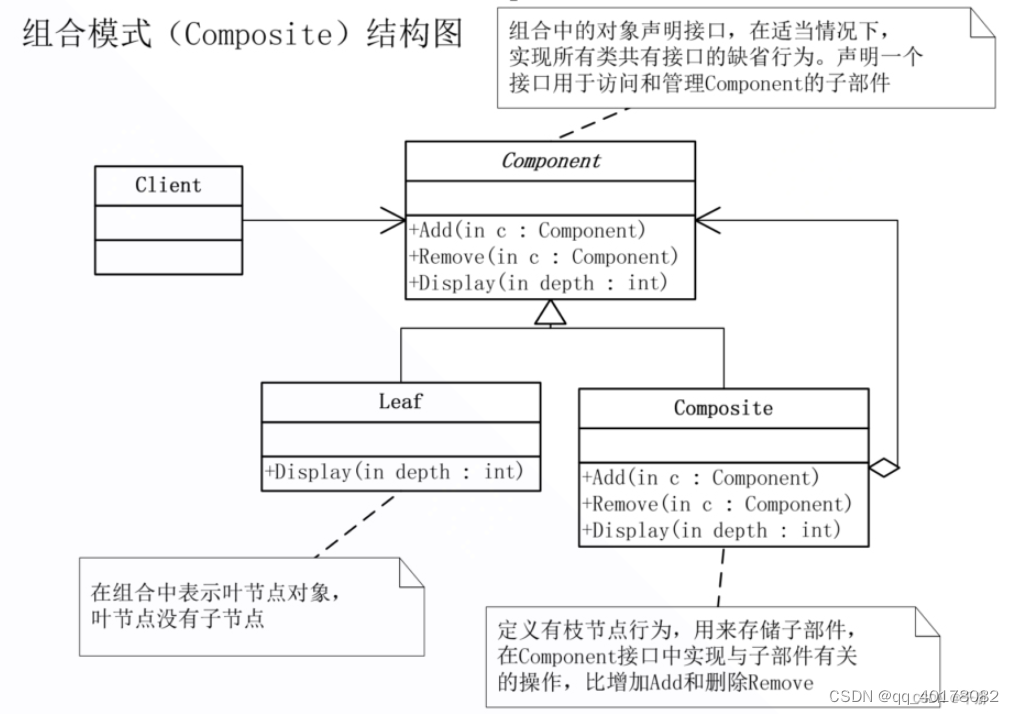
19.组合模式(Composite)
意图:将对象组成树状结构以表示“部分-整体”的层次结构,使得Client对单个对象和组合对象的使用具有一致性。 上下文:在树型结构的问题中,Client必须以不同的方式处理单个对象和组合对象。能否提供一种封装,…...

应用在IPM接口隔离领域中的光电耦合器
IPM即Intelligent Power Module(智能功率模块)的缩写,它是通过优化设计将IGBT连同其驱动电路和多种保护电路封装在同一模块内,使电力变换装置的设计者从繁琐的IGBT驱动和保护电路设计中解脱出来,大大降低了功率半导体器件的应用难度ÿ…...

rust引用
一、引用是什么 引用,又叫做借用。是一个指针类型。 引用是指向数据的指针,它允许我们以只读或可变的方式访问数据,而不获取数据的所有权。 编译器静态地保证了引用总是指向有效的对象。也就是说,当存在引用指向一个对象时&#…...
)
Android AMS——Activity Pause(八)
在前面的文章《Android AMS——ATMS解析(四)》中,介绍了 Activity 的启动流程,其中调用到 Task.resumeTopActivityInnerLocked() 时,会先调用 startPausingLocked 暂停前一个 Activity,在启动新的 Activity。 这里我们就看以下 Activity 的暂停流程。 一、Activity暂停流…...
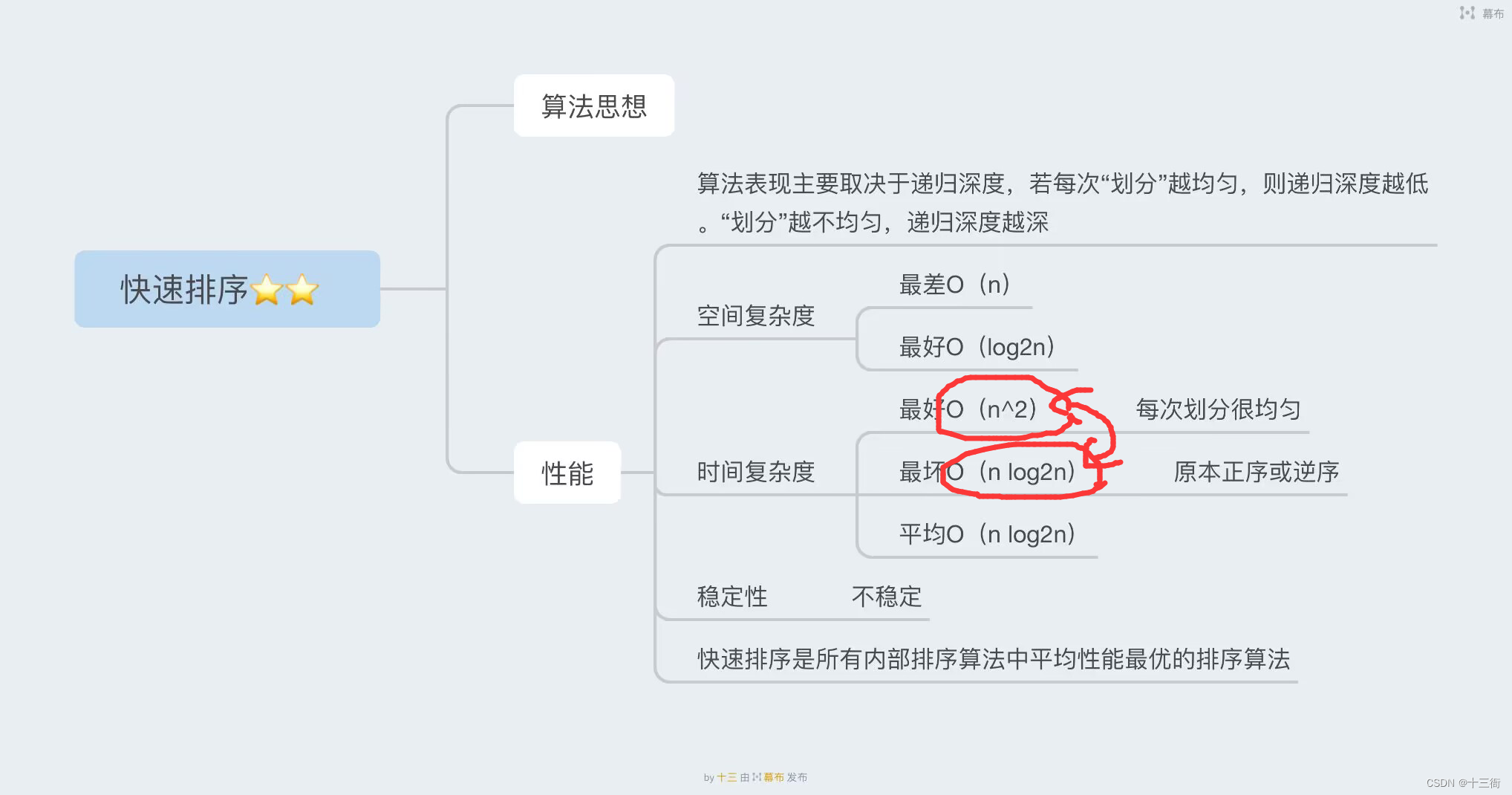
【数据结构】冒泡排序,快速排序的学习知识总结
目录 1、冒泡排序 1.1 算法思想 1.2 代码实现 方式一:顺序表 方式二:链表 2、快速排序 2.1 算法思想 2.2 代码实现 2.3 例题分析 1、冒泡排序 1.1 算法思想 冒泡排序是一种简单的排序算法,它的基本思想是从数组的第一个元素开始…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...
