Bigemap如何查看历史影像
工具
Bigemap gis office地图软件
BIGEMAP GIS Office-全能版
Bigemap APP_卫星地图APP_高清卫星地图APP
很多人都在寻找历史影像图,这块的需求是非常大,历史影像一般可以用于历史地貌的变迁分析,还原以前的生态场景,对范围面积进行对比等等。
目前有历史影像记录的官方地图只有2个(一个是ARCGIS, 一个是谷歌地图)都可以通过官方图源地址在bigemap里面添加进行查看:
谷歌地球: http://kh.google.com 包含:卫星影像、历史影像
Arcgis : https://livingatlas.arcgis.com/wayback 包含:卫星影像、历史影像
那么这里要注意的是,谷歌图源目前是没有对大陆网络ip进行开放的,所以如果需要查看,也是需要看你当前的网络是否允许查看(这个可以通过点击“谷歌地球”网址验证是否可以打开,不能访问的话,可以尝试修改自己的网络ip哦)
下面来讲一下在Bigemap里面添加的教程:
打开软件,然后点击选择地图这个按钮,列表中有个添加按钮点进去选择添加地图的方式:
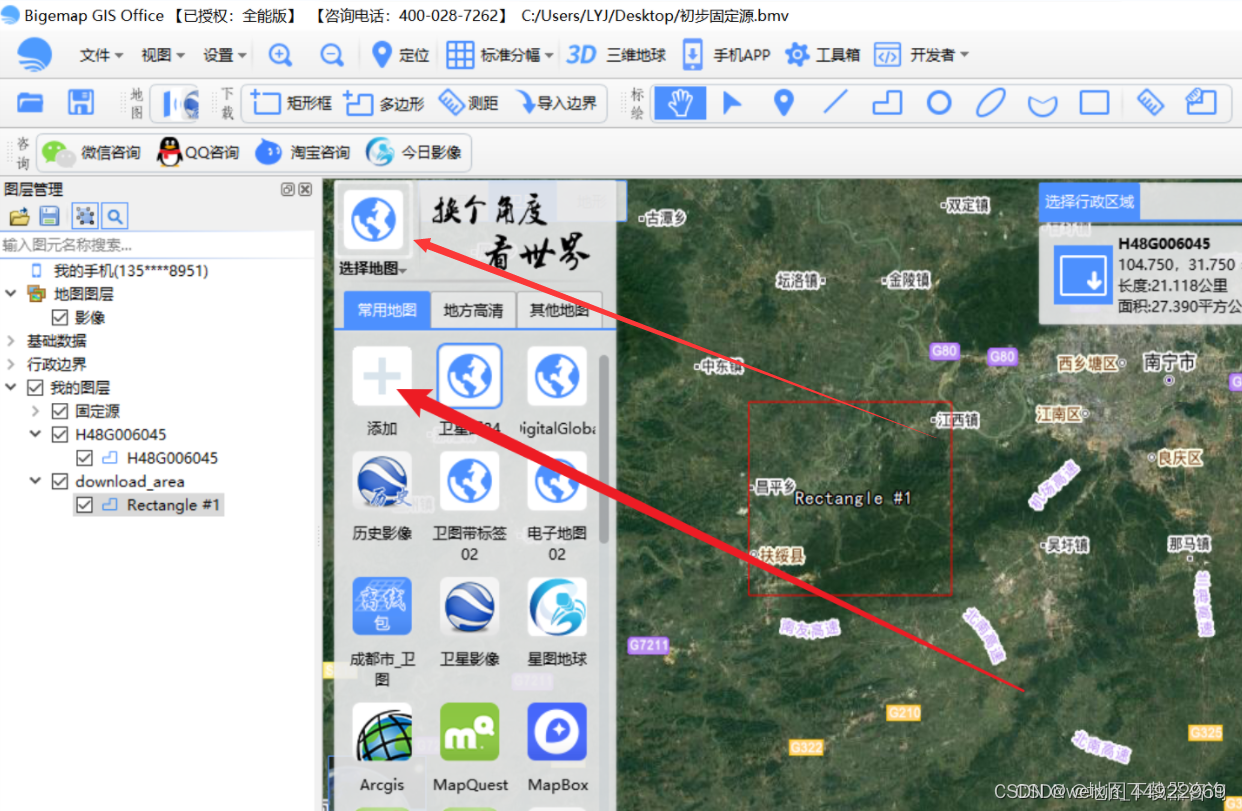
选择通过添加在线地图的方式输入谷歌地图网址添加(arcgis地图添加方式一样):
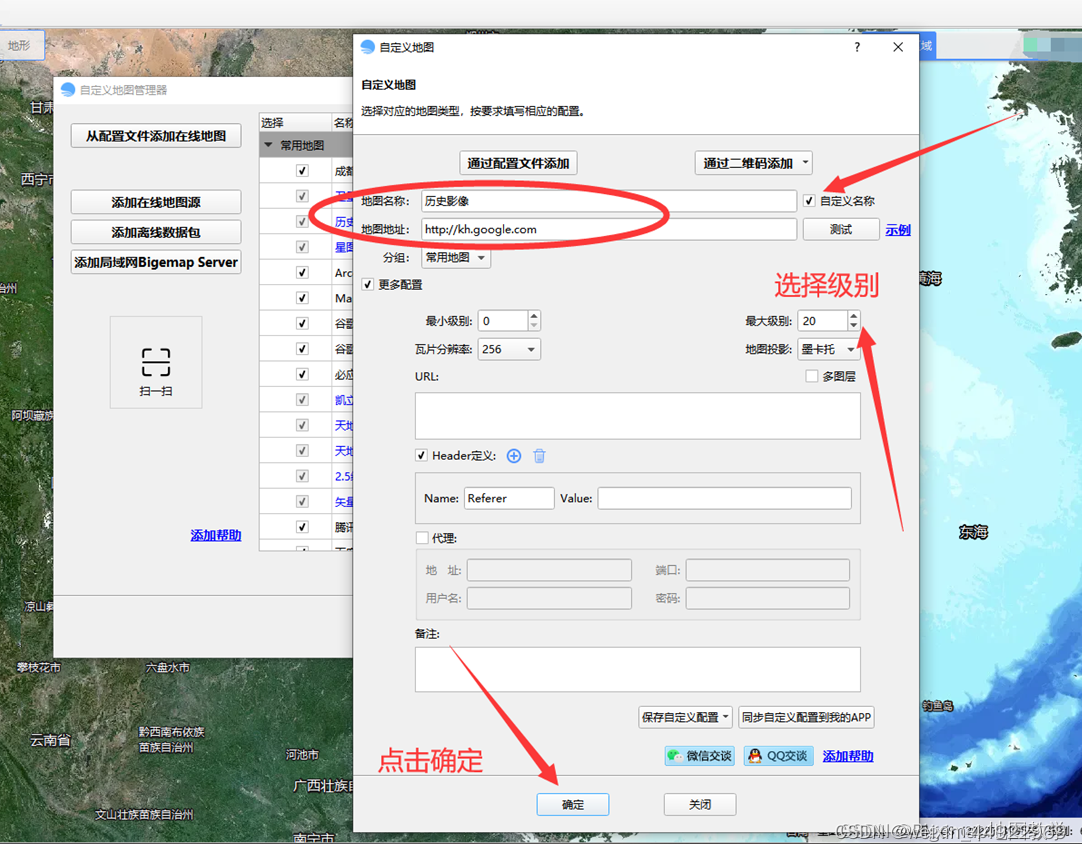
点击确定以后选择历史影像:
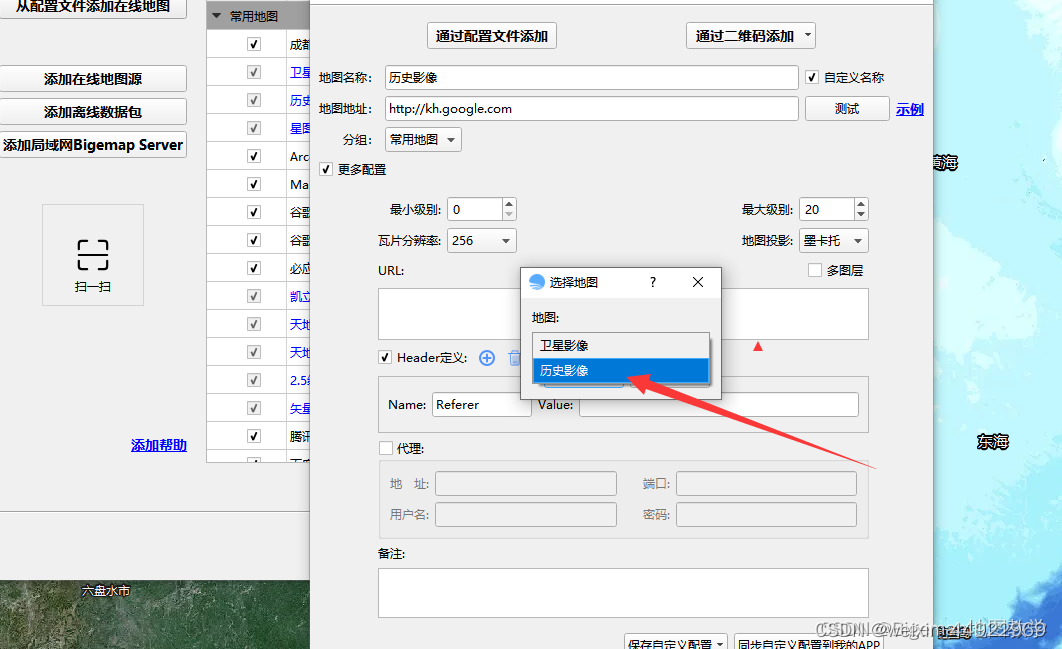
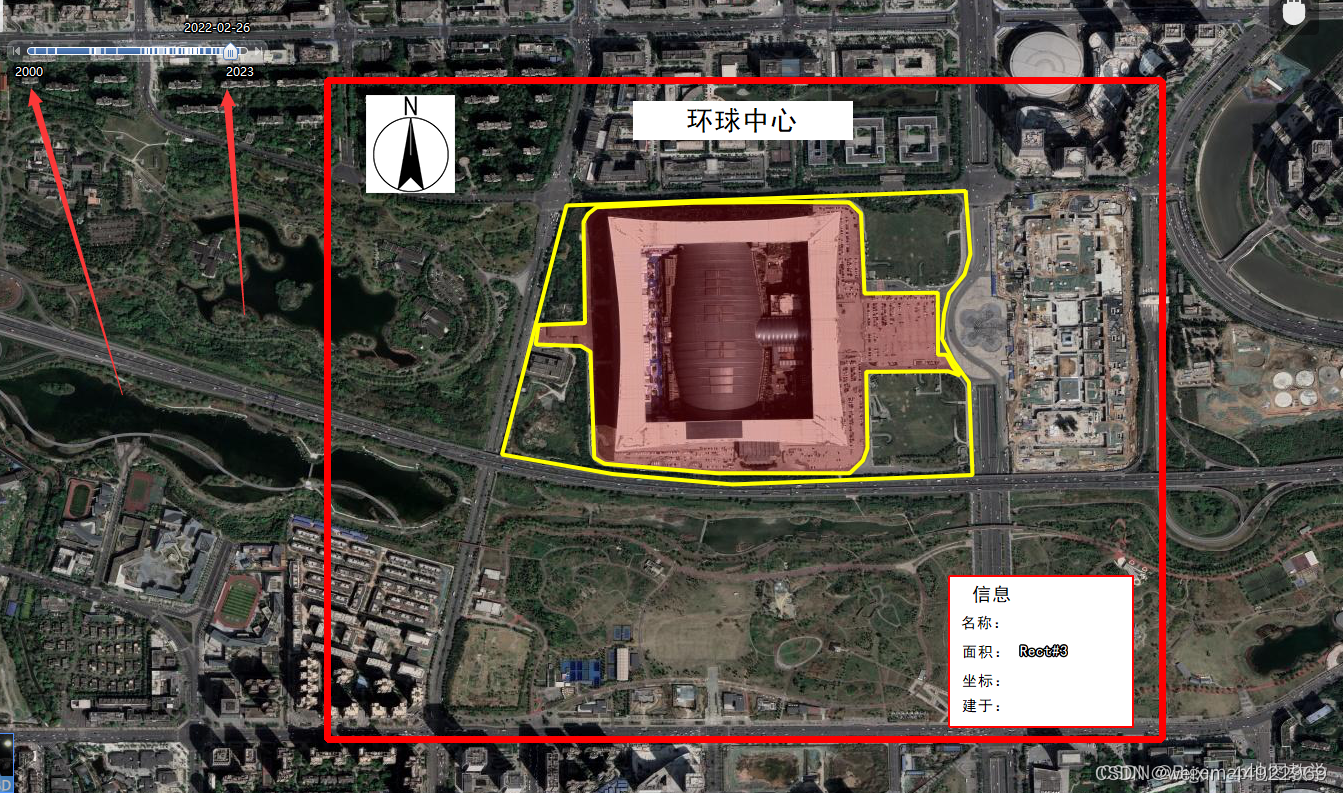
添加完成以后就可以直接拖动时间条查看啦:

可以导入自己的图纸进行对比分析:
以下是几个其他谷歌地图的地址址:
谷歌卫星地图(无偏移):
https://gac-geo.googlecnapps.cn/maps/vt?lyrs=s&x={x}&y={y}&z={z}
谷歌卫星地图(有偏移)
https://gac-geo.googlecnapps.cn/maps/vt?lyrs=s&gl=cn&x={x}&y={y}&z={z}
谷歌卫星地图带标签(有偏移)
https://gac-geo.googlecnapps.cn/maps/vt?lyrs=y&gl=cn&x={x}&y={y}&z={z}
谷歌电子地图(有偏移)
https://gac-geo.googlecnapps.cn/maps/vt?lyrs=m&x={x}&y={y}&z={z}
谷歌地形图(有偏移)
https://gac-geo.googlecnapps.cn/maps/vt?lyrs=p&x={x}&y={y}&z={z}
————————————————
相关文章:

Bigemap如何查看历史影像
工具 Bigemap gis office地图软件 BIGEMAP GIS Office-全能版 Bigemap APP_卫星地图APP_高清卫星地图APP 很多人都在寻找历史影像图,这块的需求是非常大,历史影像一般可以用于历史地貌的变迁分析,还原以前的生态场景,对范围面积…...
如何离线安装和使用pymysql操作mysql数据库
一、应用背景 在企业内部网络要使用python操作mysql数据库。然而,python未自带访问MySQL数据库的函数库pymysql,需要另外安装。网上有很多安装pymysql都需要互联网支持。本文主要阐述如何离线安装pymysql,并简要介绍pymysql如何进行mysql操作。 pymysq…...

Prometheus-监控Mysql进阶用法(1)(安装配置)
阿丹: 在开发和生产环境中有可能会出现慢mysql等问题,那么这里就需要我们优秀的程序员来进行监控和解决,那么如何借助云原生的监控系统来完成这个操作呢? 环境描述: 使用一台空白的阿里云服务器2核4G。 服务器基本安装…...
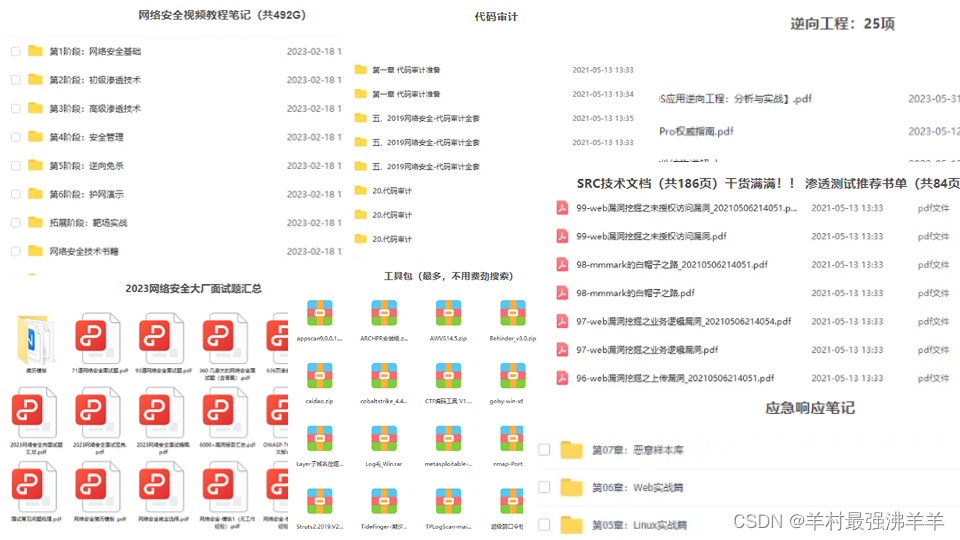
网络安全(黑客技术)自学内容
前言 一、什么是网络安全 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 无论网络、Web、移动、桌面、云等哪个领域,都有攻与防…...

linux centos7 安装mongodb7.0.1 及 mongosh2.0.1
下载数据库并解压 wget https://fastdl.mongodb.org/linux/mongodb-linux-x86_64-rhel70-7.0.1.tgz tar -zxf mongodb-linux-x86_64-rhel70-7.0.1.tgz #移动到/usr/local/mongo目录 mv mongodb-linux-x86_64-rhel70-7.0.1 /usr/local/mongodbmongosh 命令行下载 #下载命令行…...
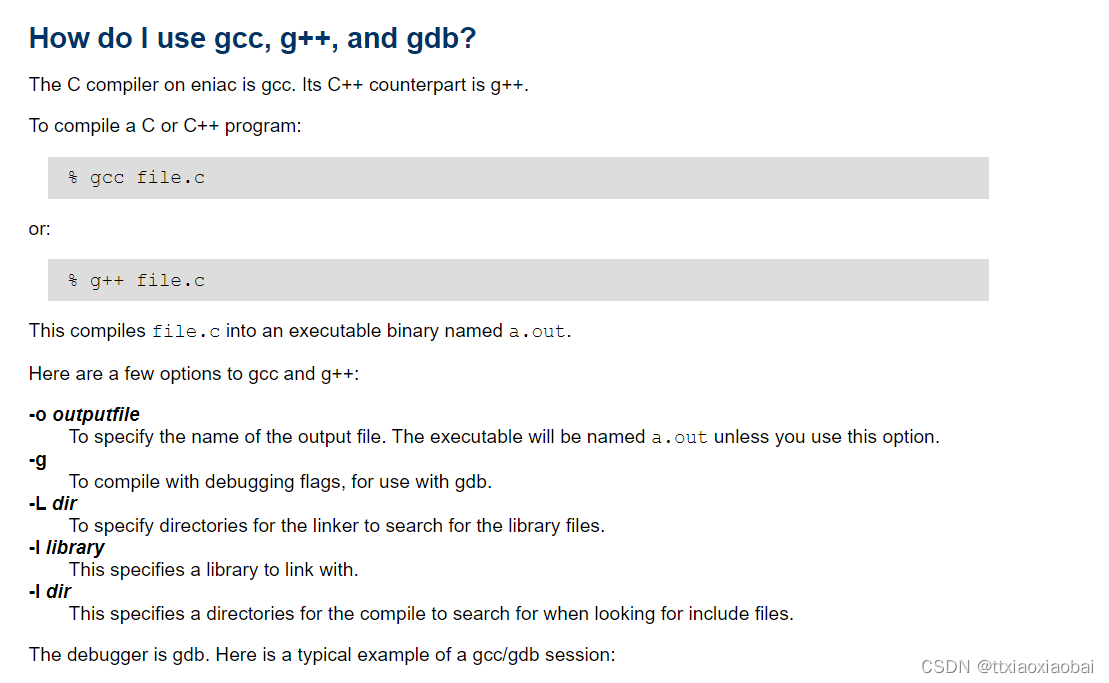
c++ | makefile | 编译 | 链接库
简单记一下 看着人家总结的挺好的 点这...

n个骰子掷出m点的概率,C++实现
一.在骰子游戏中,我们会有猜点数的问题。我们该如何用算法来描述呢? 加入我们当前只有一个骰子,我们该如何算概率呢? 我们现在开始推导一下吧: 首先是一个骰子的情况,我们可以简单的知道n个骰子一共可以掷出…...
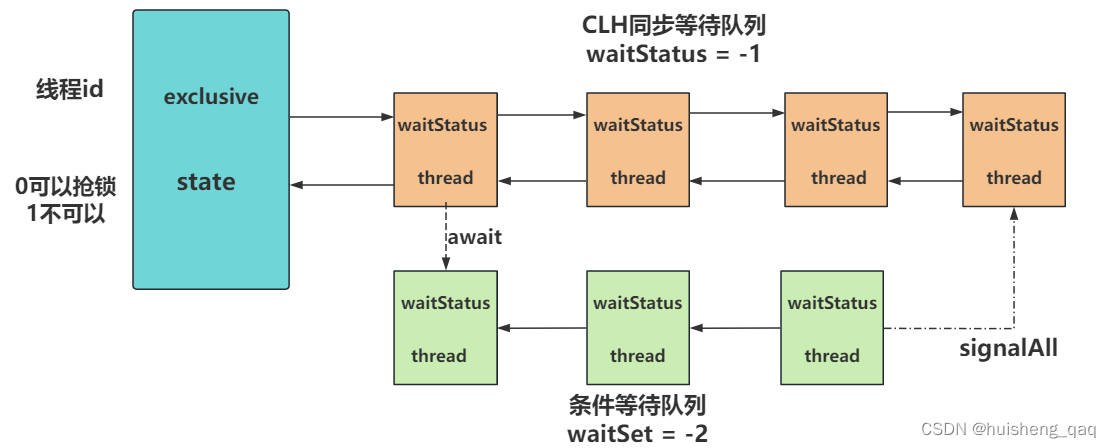
【JUC系列-08】深入理解CyclicBarrier底层原理和基本使用
JUC系列整体栏目 内容链接地址【一】深入理解JMM内存模型的底层实现原理https://zhenghuisheng.blog.csdn.net/article/details/132400429【二】深入理解CAS底层原理和基本使用https://blog.csdn.net/zhenghuishengq/article/details/132478786【三】熟练掌握Atomic原子系列基本…...
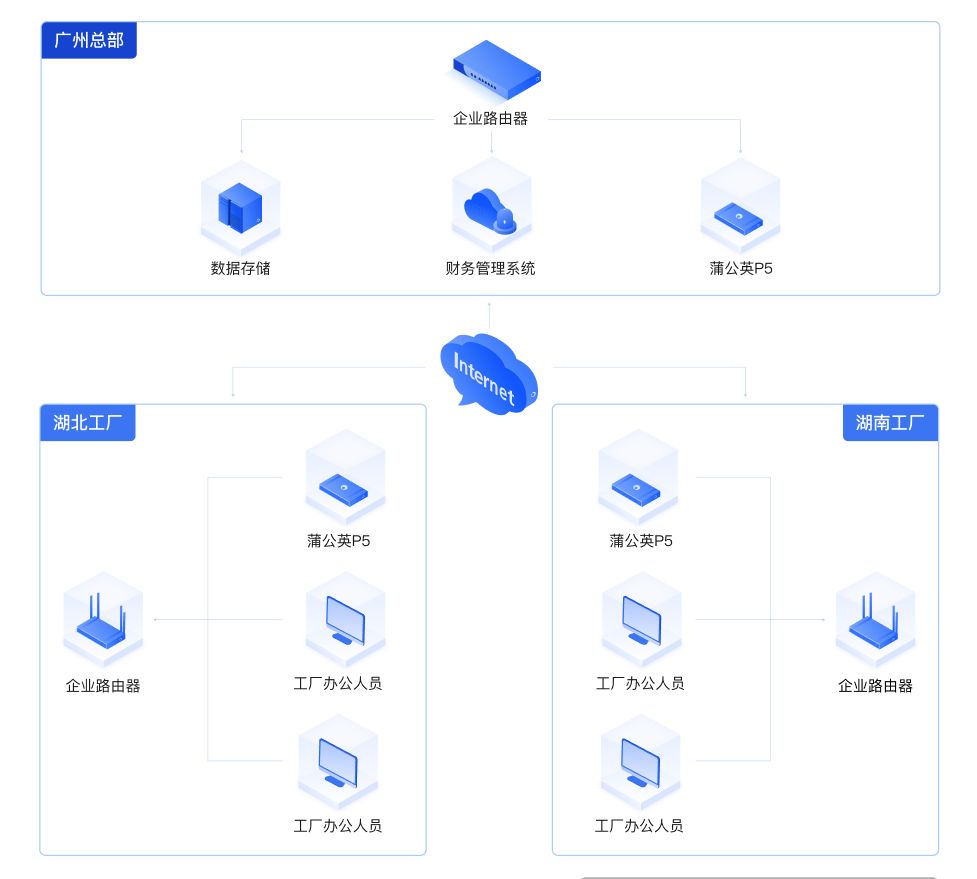
企业专线成本高?贝锐蒲公英轻松实现财务系统远程访问
在办公及信息系统领域,许多企业纷纷采用金蝶等财务管理软件来提升运营效率。以某食品制造企业为例,该企业总部位于广州,并拥有湖北仙桃工厂、广州从化工厂和湖南平江工厂三大生产基地。为提高管理效率,该企业在广州总部局域网内部…...

自学——网络安全——黑客技术
想自学网络安全(黑客技术)首先你得了解什么是网络安全!什么是黑客!!! 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队…...
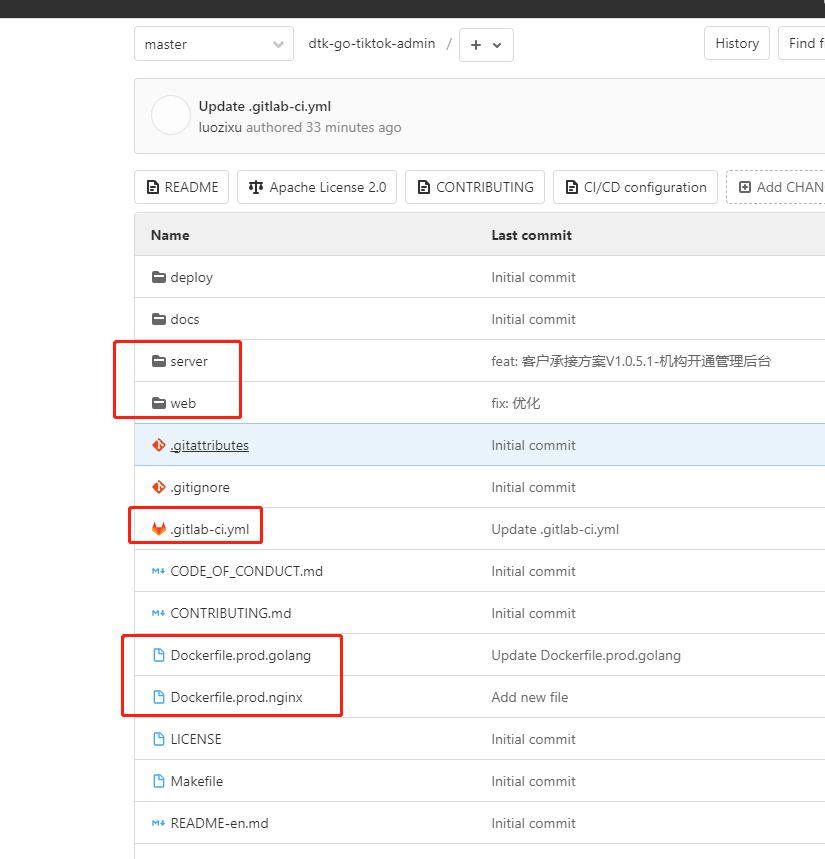
k8s部署gin-vue-admin框架、gitlab-ci、jenkins pipeline 、CICD
测试环境使用的jenkins 正式环境使用的gitlab-ci 测试环境 创建yaml文件 apiVersion: v1 kind: ConfigMap metadata:name: dtk-go-tiktok-admin-configlabels:app.kubernetes.io/name: dtk-go-tiktok-adminapp.kubernetes.io/business: infrastructureapp.kubernetes.io/run…...
【SpringBoot项目】SpringBoot+MyBatis+MySQL电脑商城
在b站听了袁老师的开发课,做了一点笔记。 01-项目环境搭建_哔哩哔哩_bilibili 基于springboot框架的电脑商城项目(一)_springboot商城项目_失重外太空.的博客-CSDN博客 项目环境搭建 1.项目分析 1.项目功能:登录、注册、热销…...
互联网医院|互联网医院系统引领医疗科技新风潮
互联网的迅速发展已经改变了人们的生活方式,而医疗领域也不例外。近年来,互联网医院应运而生,为患者和医生提供了更便捷、高效的医疗服务。本文将深入探讨互联网医院的系统特点、功能以及未来的发展方向,为您展现医疗行业的新时代…...

Mock安装及应用
1、安装 npm install mockjs 2、Mock.Random属性 该属性是一个工具类,用于生成各种随机数据。它提供的方法如下: Basic: boolean,natural,integer,float,character,string,range,date,time,datetime,now; Image: image,dataImage; Color: color; Text: p…...

一起来看看UI设计流程详解吧!通俗易懂
UI设计2023 通俗易懂的UI设计流程详解 首先,大家要明确一下范围:一般分为新产品的从0-1和已有产品上新的模块或功能的从0-1,这两个方向的环节和产出物会有比较大的区别。其实在UI设计师介入之前,我们是需要去了解一些大的方向和…...

TikTok营销成功秘籍:ROI指标的黄金法则
在当今数字营销领域,TikTok已经崭露头角,成为了品牌和营销者们争相追逐的热门平台。 然而,要在TikTok上取得成功,不仅需要创意和内容,还需要精确的ROI(投资回报率)指标来衡量和优化你的营销策略…...
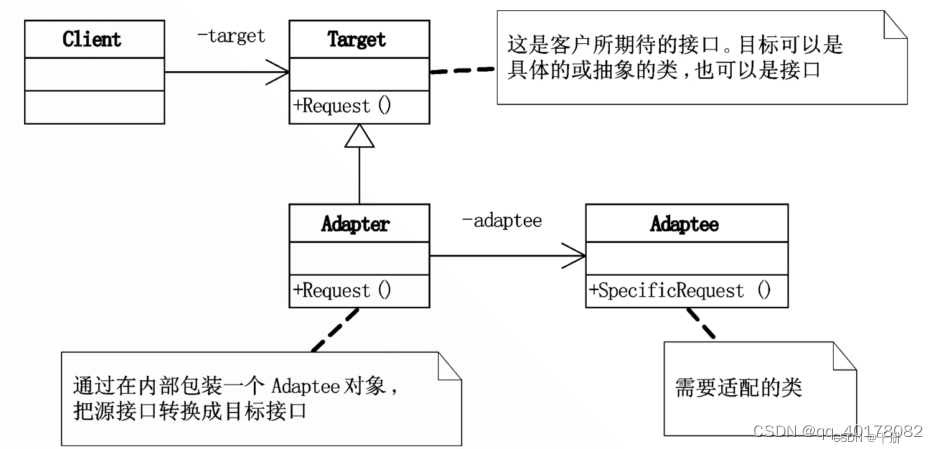
17.适配器模式(Adapter)
意图:将一个类的接口转换为Client希望的另一个接口,使得原本由于接口不兼容而不能一起工作的那些类在一起工作。 UML图 Target:定义Client使用的与特定领域相关的接口。 Client:与符合Target接口的对象协同工作。 Adaptee…...

leetcode做题笔记154. 寻找旋转排序数组中的最小值 II
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,4,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,4]若旋转 7 次࿰…...
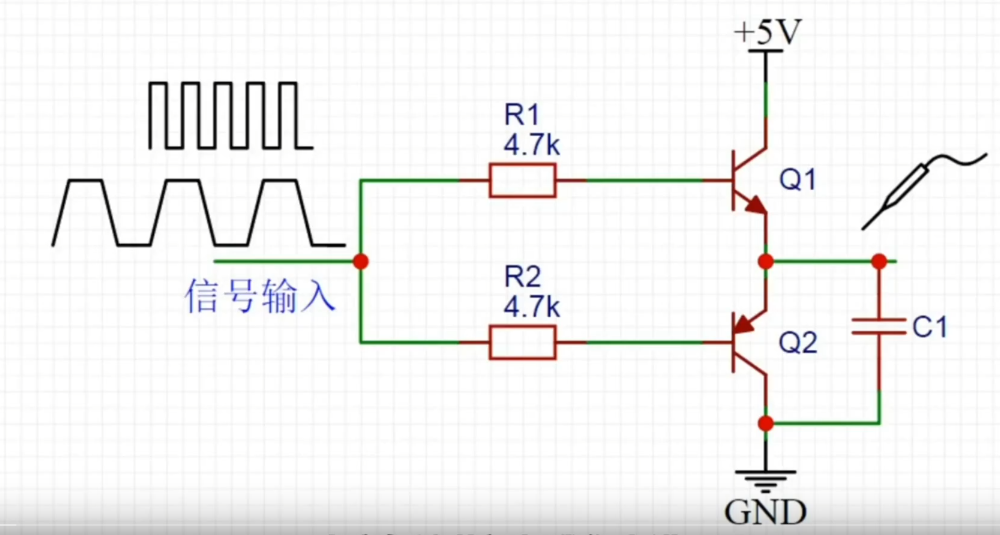
什么是推挽电路?
推挽电路原理: 可以简单理解为推和拉; 此电路总共用到两个元器件,对应图中的Q1----NPN三极管,Q2----PNP三极管,两个电阻R1和R2起到限流的作用;两个三极管的中间对应信号的输出。 下面就举例说明是如何工作的…...
:窗口的使用,处理函数的使用)
208.Flink(三):窗口的使用,处理函数的使用
目录 一、窗口 1.窗口的概念 2.窗口的分类 (1)按照驱动类型分 (2)按照窗口分配数据的规则分类 3.窗口api概览 (1)按键分区(Keyed)和非按键分区(Non-Keyed) *1)按键分区窗口(Keyed Windows) *2)非按键分区(Non-Keyed Windows) (2)代码中窗口API的调…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
