深度学习-一个简单的深度学习推导
文章目录
- 前言
- 1.sigmod函数
- 2.sigmoid求导
- 3.损失函数loss
- 4.神经网络
- 1.神经网络结构
- 2.公式表示-正向传播
- 3.梯度计算
- 1.Loss 函数
- 2.梯度
- 1.反向传播第2-3层
- 2.反向传播第1-2层
- 3.python代码
- 4.MNIST 数据集
前言
本章主要推导一个简单的两层神经网络。
其中公式入口【入口】
1.sigmod函数
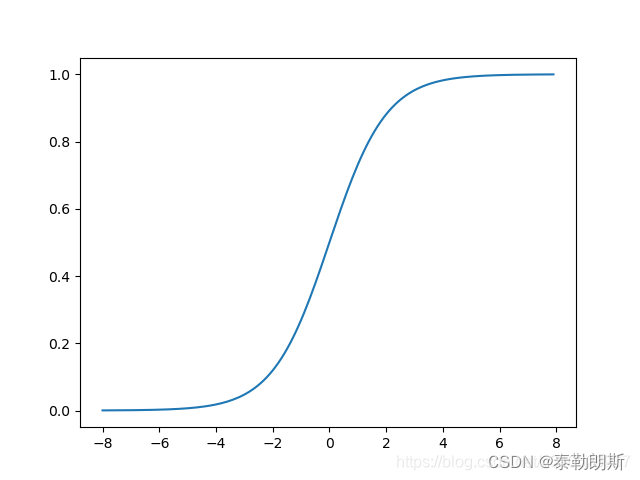
激活函数我们选择sigmod,其如下:
f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
其图形为:
可以用python表示:
def sigmoid(x):return 1.0/(1.0+np.exp(-x))
2.sigmoid求导
先看一个复合函数求导:
如果 y ( u ) = f ( u ) , u ( x ) = g ( x ) , 那么 d y d x = d y d u ∗ d u d x 如果y(u)=f(u),u(x)=g(x), 那么\frac{dy}{dx}=\frac{dy}{du} * \frac{du}{dx} 如果y(u)=f(u),u(x)=g(x),那么dxdy=dudy∗dxdu
那么对于sigmoid函数求导:
f ( x ) = 1 1 + e − x , 那么假设 g ( x ) = 1 + e − x , f ( x ) = 1 g ( x ) f ( x ) ‘ = − 1 g ( x ) 2 ∗ ( − e − x ) = e − x ( 1 + e − x ) 2 = f ( x ) ∗ ( 1 − f ( x ) ) f(x)=\frac{1}{1+e^{-x}},\\ 那么假设g(x)=1+e^{-x}, \\ f(x)=\frac{1}{g(x)}\\ f(x)^`=\frac{-1}{g(x)^2}*{(-e^{-x})}=\frac{e^{-x}}{(1+e^{-x})^{2}}=f(x)*(1-f(x)) f(x)=1+e−x1,那么假设g(x)=1+e−x,f(x)=g(x)1f(x)‘=g(x)2−1∗(−e−x)=(1+e−x)2e−x=f(x)∗(1−f(x))
如果用python表达:
def sigmoid_prime(x):"""sigmoid 函数的导数"""return sigmoid(x)*(1-sigmoid(x))
3.损失函数loss
L o s s = 1 2 ∗ ( y ˘ − y ) 2 Loss=\frac{1}{2}*{(\breve{y}-y)}^2 Loss=21∗(y˘−y)2
它的导数,
L o s s ‘ = y ˘ − y Loss^`=\breve{y}-y Loss‘=y˘−y
4.神经网络
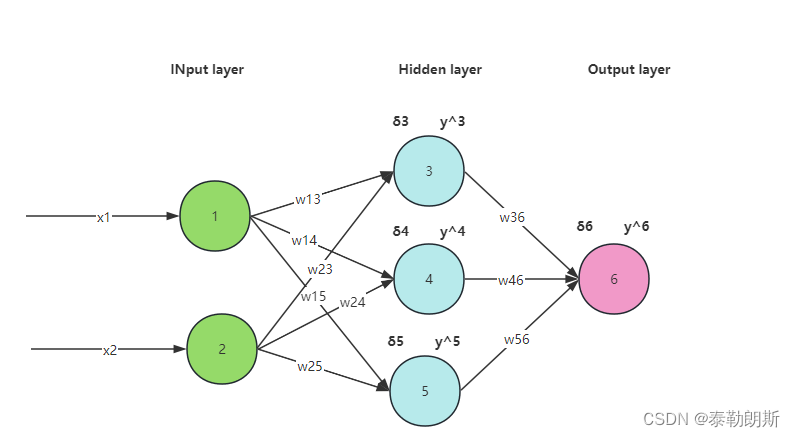
1.神经网络结构
本次我们采用如下神经网络:

2.公式表示-正向传播
w 13 ∗ x 1 + w 23 ∗ x 2 + b 1 = σ 3 , 那么 y 3 ˘ = s i g m o i d ( σ 3 ) w 14 ∗ x 1 + w 24 ∗ x 2 + b 2 = σ 4 , 那么 y 4 ˘ = s i g m o i d ( σ 4 ) w 15 ∗ x 1 + w 25 ∗ x 2 + b 3 = σ 5 , 那么 y 5 ˘ = s i g m o i d ( σ 5 ) 同理可得, w 36 ∗ y 3 ˘ + w 46 ∗ y 4 ˘ + w 56 ∗ y 5 ˘ + b 4 = σ 6 , 那么 y 6 ˘ = s i g m o i d ( σ 6 ) w_{13}*x_1+w_{23}*x_2+b_1=\sigma_3, 那么\breve{y_3}=sigmoid(\sigma_3)\\ w_{14}*x_1+w_{24}*x_2+b_2=\sigma_4, 那么\breve{y_4}=sigmoid(\sigma_4)\\ w_{15}*x_1+w_{25}*x_2+b_3=\sigma_5, 那么\breve{y_5}=sigmoid(\sigma_5)\\ 同理可得,\\ w_{36}*\breve{y_3}+w_{46}*\breve{y_4}+w_{56}*\breve{y_5}+b_4=\sigma_6, 那么\breve{y_6}=sigmoid(\sigma_6)\\ w13∗x1+w23∗x2+b1=σ3,那么y3˘=sigmoid(σ3)w14∗x1+w24∗x2+b2=σ4,那么y4˘=sigmoid(σ4)w15∗x1+w25∗x2+b3=σ5,那么y5˘=sigmoid(σ5)同理可得,w36∗y3˘+w46∗y4˘+w56∗y5˘+b4=σ6,那么y6˘=sigmoid(σ6)
上面的公式我们用矩阵表示:
[ x 1 x 2 ] ⋅ [ w 13 w 14 w 15 w 23 w 24 w 25 ] + [ b 1 b 2 b 3 ] = [ w 13 ∗ x 1 + w 23 ∗ x 2 + b 1 w 14 ∗ x 1 + w 24 ∗ x 2 + b 2 w 15 ∗ x 1 + w 25 ∗ x 2 + b 3 ] = [ σ 3 σ 4 σ 5 ] 代入激活函数, [ s i g m o i d ( σ 3 ) s i g m o i d ( σ 4 ) s i g m o i d ( σ 5 ) ] = [ y 3 ˘ y 4 ˘ y 5 ˘ ] [ y 3 ˘ y 4 ˘ y 5 ˘ ] ⋅ [ w 36 w 46 w 56 ] + [ b 4 ] = [ w 36 ∗ y 3 ˘ + w 46 ∗ y 4 ˘ + w 56 ∗ y 5 ˘ + b 4 ] = σ 6 , s i g m o i d ( σ 6 ) = y ˘ 6 \left[\begin {array}{c} x_1 &x_2 \\ \end{array}\right] \cdot \left[\begin {array}{c} w_{13} &w_{14} & w_{15} \\ w_{23} &w_{24} & w_{25} \\ \end{array}\right]+ \left[\begin {array}{c} b_{1} \\ b_{2} \\ b_{3} \\ \end{array}\right]= \left[\begin {array}{c} w_{13}*x_1+w_{23}*x_2+b_1\\ w_{14}*x_1+w_{24}*x_2+b_2\\ w_{15}*x_1+w_{25}*x_2+b_3\\ \end{array}\right]= \left[\begin {array}{c} \sigma_{3} \\ \sigma_{4} \\ \sigma_{5} \\ \end{array}\right]\\ 代入激活函数,\\ \left[\begin {array}{c} sigmoid(\sigma_3) \\ sigmoid(\sigma_4) \\ sigmoid(\sigma_5) \\ \end{array}\right]= \left[\begin {array}{c} \breve{y_3} \\ \breve{y_4}\\ \breve{y_5} \\ \end{array}\right]\\ \left[\begin {array}{c}\\ \breve{y_3} &\breve{y_4} &\breve{y_5} \\ \end{array}\right] \cdot \left[\begin {array}{c} w_{36} \\ w_{46} \\ w_{56} \\ \end{array}\right]+ \left[\begin {array}{c} b_{4} \\ \end{array}\right]= \left[\begin {array}{c} w_{36}*\breve{y_3}+w_{46}*\breve{y_4}+w_{56}*\breve{y_5}+b_4 \\ \end{array}\right]=\sigma_6\\ ,\\ sigmoid(\sigma_6)=\breve{y}_6 [x1x2]⋅[w13w23w14w24w15w25]+ b1b2b3 = w13∗x1+w23∗x2+b1w14∗x1+w24∗x2+b2w15∗x1+w25∗x2+b3 = σ3σ4σ5 代入激活函数, sigmoid(σ3)sigmoid(σ4)sigmoid(σ5) = y3˘y4˘y5˘ [y3˘y4˘y5˘]⋅ w36w46w56 +[b4]=[w36∗y3˘+w46∗y4˘+w56∗y5˘+b4]=σ6,sigmoid(σ6)=y˘6
3.梯度计算
1.Loss 函数
L o s s = 1 2 ∗ ( y ˘ 6 − y 6 ) 2 Loss=\frac{1}{2}*{(\breve{y}_6-y_6)}^2 Loss=21∗(y˘6−y6)2
2.梯度
1.反向传播第2-3层
[ ∂ l ∂ w 36 ∂ l ∂ w 46 ∂ l ∂ w 56 ] = [ ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ w 36 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ w 46 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ w 56 ] = [ ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ y ˘ 3 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ y ˘ 4 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ y ˘ 5 ] \left[\begin {array}{c} \frac{\partial{l}}{\partial{w_{36}}} \\ \\ \frac{\partial{l}}{\partial{w_{46}}} \\ \\ \frac{\partial{l}}{\partial{w_{56}}} \\ \end{array}\right]= \left[\begin {array}{c} \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{w_{36}}} \\ \\ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{w_{46}}} \\ \\ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{w_{56}}} \\ \end{array}\right]= \left[\begin {array}{c} (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*\breve{y}_3\\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*\breve{y}_4\\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*\breve{y}_5\\ \end{array}\right] \\ ∂w36∂l∂w46∂l∂w56∂l = ∂y˘6∂l∗∂σ6∂y˘6∗∂w36∂σ6∂y˘6∂l∗∂σ6∂y˘6∗∂w46∂σ6∂y˘6∂l∗∂σ6∂y˘6∗∂w56∂σ6 = (y˘6−y6)∗S(σ6)∗(1−S(σ6))∗y˘3(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗y˘4(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗y˘5
上面的式子中 S ( x ) = 1 1 + e − x S(x)=\frac{1}{1+e^{-x}} S(x)=1+e−x1,其中 σ 6 \sigma_6 σ6通过正向传播可以计算出来,具体细节看2式。
根据公式2,我们已经知道 y ˘ 6 \breve{y}_6 y˘6和 y ˘ 3 \breve{y}_3 y˘3的值,所以上面的权重偏导数就能计算出来了。
下面求bias的偏导数, ∂ l ∂ b 4 \frac{\partial{l}}{\partial{b_4}} ∂b4∂l.
∂ l ∂ b 4 = ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ b 4 = ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) \frac{\partial{l}}{\partial{b_4}}= \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{b_4}} = (\breve{y}_6-y_6)* S(\sigma_6)*(1-S(\sigma_6)) ∂b4∂l=∂y˘6∂l∗∂σ6∂y˘6∗∂b4∂σ6=(y˘6−y6)∗S(σ6)∗(1−S(σ6))
2.反向传播第1-2层
权重
[ ∂ l ∂ w 13 ∂ l ∂ w 23 ∂ l ∂ w 14 ∂ l ∂ w 24 ∂ l ∂ w 15 ∂ l ∂ w 25 ] = [ ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 3 ∗ ∂ y ˘ 3 ∂ σ 3 ∗ ∂ σ 3 ∂ w 13 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 3 ∗ ∂ y ˘ 3 ∂ σ 3 ∗ ∂ σ 3 ∂ w 23 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 4 ∗ ∂ y ˘ 4 ∂ σ 4 ∗ ∂ σ 4 ∂ w 14 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 4 ∗ ∂ y ˘ 4 ∂ σ 4 ∗ ∂ σ 4 ∂ w 24 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 5 ∗ ∂ y ˘ 5 ∂ σ 5 ∗ ∂ σ 5 ∂ w 15 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 5 ∗ ∂ y ˘ 5 ∂ σ 5 ∗ ∂ σ 5 ∂ w 25 ] = . . [ ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 36 ∗ S ( σ 3 ) ∗ ( 1 − S ( σ 3 ) ) ∗ x 1 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 36 ∗ S ( σ 3 ) ∗ ( 1 − S ( σ 3 ) ) ∗ x 2 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 46 ∗ S ( σ 4 ) ∗ ( 1 − S ( σ 4 ) ) ∗ x 1 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 46 ∗ S ( σ 4 ) ∗ ( 1 − S ( σ 4 ) ) ∗ x 2 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 56 ∗ S ( σ 5 ) ∗ ( 1 − S ( σ 5 ) ) ∗ x 1 ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 56 ∗ S ( σ 5 ) ∗ ( 1 − S ( σ 5 ) ) ∗ x 2 ] \left[\begin {array}{c} \frac{\partial{l}}{\partial{w_{13}}} & \frac{\partial{l}}{\partial{w_{23}}} \\ \\ \frac{\partial{l}}{\partial{w_{14}}} & \frac{\partial{l}}{\partial{w_{24}}}\\ \\ \frac{\partial{l}}{\partial{w_{15}}} & \frac{\partial{l}}{\partial{w_{25}}}\\ \end{array}\right]= \left[\begin {array}{c} \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{3}}} * \frac{\partial{\breve{y}_3}}{\partial{\sigma_{3}}} * \frac{\partial{\sigma_3}}{\partial{w_{13}}} & \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{3}}} * \frac{\partial{\breve{y}_3}}{\partial{\sigma_{3}}} * \frac{\partial{\sigma_3}}{\partial{w_{23}}} \\ \\ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{4}}} * \frac{\partial{\breve{y}_4}}{\partial{\sigma_{4}}} * \frac{\partial{\sigma_4}}{\partial{w_{14}}} & \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{4}}} * \frac{\partial{\breve{y}_4}}{\partial{\sigma_{4}}} * \frac{\partial{\sigma_4}}{\partial{w_{24}}} \\ \\ \ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{5}}} * \frac{\partial{\breve{y}_5}}{\partial{\sigma_{5}}} * \frac{\partial{\sigma_5}}{\partial{w_{15}}} & \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{5}}} * \frac{\partial{\breve{y}_5}}{\partial{\sigma_{5}}} * \frac{\partial{\sigma_5}}{\partial{w_{25}}} \\ \end{array}\right]=\\ .\\ .\\ \left[\begin {array}{c} (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{36}*S(\sigma_3)*(1-S(\sigma_3))*x_1 & (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{36}*S(\sigma_3)*(1-S(\sigma_3))*x_2 \\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{46}*S(\sigma_4)*(1-S(\sigma_4))*x_1 & (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{46}*S(\sigma_4)*(1-S(\sigma_4))*x_2 \\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{56}*S(\sigma_5)*(1-S(\sigma_5))*x_1 & (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{56}*S(\sigma_5)*(1-S(\sigma_5))*x_2 \end{array}\right] \\ ∂w13∂l∂w14∂l∂w15∂l∂w23∂l∂w24∂l∂w25∂l = ∂y˘6∂l∗∂σ6∂y˘6∗∂y˘3∂σ6∗∂σ3∂y˘3∗∂w13∂σ3∂y˘6∂l∗∂σ6∂y˘6∗∂y˘4∂σ6∗∂σ4∂y˘4∗∂w14∂σ4 ∂y˘6∂l∗∂σ6∂y˘6∗∂y˘5∂σ6∗∂σ5∂y˘5∗∂w15∂σ5∂y˘6∂l∗∂σ6∂y˘6∗∂y˘3∂σ6∗∂σ3∂y˘3∗∂w23∂σ3∂y˘6∂l∗∂σ6∂y˘6∗∂y˘4∂σ6∗∂σ4∂y˘4∗∂w24∂σ4∂y˘6∂l∗∂σ6∂y˘6∗∂y˘5∂σ6∗∂σ5∂y˘5∗∂w25∂σ5 =.. (y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w36∗S(σ3)∗(1−S(σ3))∗x1(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w46∗S(σ4)∗(1−S(σ4))∗x1(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w56∗S(σ5)∗(1−S(σ5))∗x1(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w36∗S(σ3)∗(1−S(σ3))∗x2(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w46∗S(σ4)∗(1−S(σ4))∗x2(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w56∗S(σ5)∗(1−S(σ5))∗x2
偏置
[ ∂ l ∂ b 1 ∂ l ∂ b 2 ∂ l ∂ b 3 ] = [ ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 3 ∗ ∂ y ˘ 3 ∂ σ 3 ∗ ∂ σ 3 ∂ b 1 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 4 ∗ ∂ y ˘ 4 ∂ σ 4 ∗ ∂ σ 4 ∂ b 2 ∂ l ∂ y ˘ 6 ∗ ∂ y ˘ 6 ∂ σ 6 ∗ ∂ σ 6 ∂ y ˘ 5 ∗ ∂ y ˘ 5 ∂ σ 5 ∗ ∂ σ 5 ∂ b 3 ] = . [ ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 36 ∗ S ( σ 3 ) ∗ ( 1 − S ( σ 3 ) ) ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 46 ∗ S ( σ 4 ) ∗ ( 1 − S ( σ 4 ) ) ( y ˘ 6 − y 6 ) ∗ S ( σ 6 ) ∗ ( 1 − S ( σ 6 ) ) ∗ w 56 ∗ S ( σ 5 ) ∗ ( 1 − S ( σ 5 ) ) ] \left[\begin {array}{c} \frac{\partial{l}}{\partial{b_1}} \\ \\ \frac{\partial{l}}{\partial{b_2}} \\ \\ \frac{\partial{l}}{\partial{b_3}} \\ \end{array}\right]= \left[\begin {array}{c} \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{3}}} * \frac{\partial{\breve{y}_3}}{\partial{\sigma_{3}}} * \frac{\partial{\sigma_3}}{\partial{b_1}} \\ \\ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{4}}} * \frac{\partial{\breve{y}_4}}{\partial{\sigma_{4}}} * \frac{\partial{\sigma_4}}{\partial{b_2}} \\ \\ \ \frac{\partial{l}}{\partial{\breve{y}_6}} * \frac{\partial{\breve{y}_6}}{\partial{\sigma_6}} * \frac{\partial{\sigma_6}}{\partial{\breve{y}_{5}}} * \frac{\partial{\breve{y}_5}}{\partial{\sigma_{5}}} * \frac{\partial{\sigma_5}}{\partial{b_3}} \\ \end{array}\right]=\\ .\\ \left[\begin {array}{c} (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{36}*S(\sigma_3)*(1-S(\sigma_3)) \\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{46}*S(\sigma_4)*(1-S(\sigma_4)) \\ \\ (\breve{y}_6-y_6)*S(\sigma_6)*(1-S(\sigma_6))*w_{56}*S(\sigma_5)*(1-S(\sigma_5)) \end{array}\right] \\ ∂b1∂l∂b2∂l∂b3∂l = ∂y˘6∂l∗∂σ6∂y˘6∗∂y˘3∂σ6∗∂σ3∂y˘3∗∂b1∂σ3∂y˘6∂l∗∂σ6∂y˘6∗∂y˘4∂σ6∗∂σ4∂y˘4∗∂b2∂σ4 ∂y˘6∂l∗∂σ6∂y˘6∗∂y˘5∂σ6∗∂σ5∂y˘5∗∂b3∂σ5 =. (y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w36∗S(σ3)∗(1−S(σ3))(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w46∗S(σ4)∗(1−S(σ4))(y˘6−y6)∗S(σ6)∗(1−S(σ6))∗w56∗S(σ5)∗(1−S(σ5))
综上所述,通过反向传播,就可以计算出偏导数了。
3.python代码
根据上面的分析,下面我们写一下python代码,代码就很简单了
import numpy as np
import random
import os"""核心就是如何布局biases和weights这两个矩阵"""class Network(object):"""列表sizes包含对应层的神经元数目,如果列表是[2,3,1],那么就是指一个三层神经网络,第一层有2个神经元,第二层有3个神经元,第三次有1个神经元."""def __init__(self, sizes):"""这里num_layers是3"""self.num_layers=len(sizes)self.sizes=sizes"""随机初始化偏差,初始化后如下[array([[-1.17963885],[ 0.41953645],[-0.88551629]]), array([[0.20600121]])]特别注意这里是3x1的一个矩阵"""self.biases=[np.random.randn(y,1) for y in sizes[1:]]"""随机初始化权重[array([[-0.25009885, -0.33699188],[-0.53513364, -1.57623694],[ 1.89456316, 0.66985265]]), array([[-0.18411963, -0.08143799, 0.53533203]])]上面两个矩阵是3x2,1x3"""self.weights=[np.random.randn(y,x) for x,y in zip(sizes[:-1],sizes[1:])]def feedforward(self,x):"""输入可以认为是一个2x1的向量,因为列才是向量比如下面的点积,[3x2]*[2*1] + [3*1] = [3*1]"""a=np.array(x).reshape(len(x),1)for b, w in zip(self.biases,self.weights):a=sigmoid(np.dot(w,a)+b)return adef SGD(self,training_data,epochs,mini_batch_size,eta,test_data=None):"""使用小批量随机梯度下降算法训练神经网络,使用training_data是由训练输入和目标输出的元组(x,y)组成。"""if(test_data):n_test=len(test_data)n=len(training_data)for j in range(epochs):random.shuffle(training_data)mini_batchs=[training_data[k:k+mini_batch_size]for k in range(0,n,mini_batch_size)]for mini_batch in mini_batchs:self.update_mini_batch(mini_batch,eta)if test_data:print("Epoch {0}:{1}/{2}".format(j,self.evaluate(test_data),n_test))else:print("Epoch {0} complete.".format(j))def update_mini_batch(self,mini_batch,eta):"""使用小批量应用梯度下降算法和反向传播算法来更新神经网络的权重和偏置。mini_batch是又若干元组组成的(x,y)组成的列表,eta为学习率。其中x为batch * 2 * 1"""nabla_b=[np.zeros(b.shape) for b in self.biases]nablea_w=[np.zeros(w.shape) for w in self.weights]for x,y in mini_batch:"""计算梯度"""delta_nabla_b,delta_nable_w=self.backprob(x,y)nabla_b=[nb+dnb for nb,dnb in zip(nabla_b,delta_nabla_b)]nablea_w=[nw+dnw for nw,dnw in zip(nablea_w,nablea_w)]self.weights=[w-(eta/len(mini_batch)) * nw for w,nw in zip(self.weights,nablea_w)]self.biases=[b-(eta/len(mini_batch)) * nb for b,nb in zip(self.biases,nabla_b)]def backprob(self,a,b):nabla_b=[np.zeros(b.shape) for b in self.biases]nabla_w=[np.zeros(w.shape) for w in self.weights]x=np.array(a).reshape(len(a),1)y=np.array(b).reshape(len(b),1)activation=xactivations=[x]zs=[]"""正向传播biases 是[3x1,1x1]weights是[3x2,1x3]第1-2层的计算[3x2] * [2*1] + [3x1] = [3x1]第2-3层的计算[1x3] * [3x1] + [1x1] = [1x1] """for b,w in zip(self.biases,self.weights):z=np.dot(w,activation) + b"""未激活"""zs.append(z)"""激活函数"""activation=sigmoid(z)activations.append(activation)"""反向传播,计算最后2层的梯度"""delta=self.cost_derivative(activations[-1],y) * sigmoid_prime(zs[-1])nabla_b[-1]=deltanabla_w[-1]=np.dot(delta,activations[-2].transpose())"""反向传播,计算其余层梯度"""for l in range(2,self.num_layers):z=zs[-l]sp=sigmoid_prime(z)delta=np.dot(self.weights[-l+1].transpose(),delta) * spnabla_b[-l] =deltanabla_w[-l] = np.dot(delta,activations[-l-1].transpose())return (nabla_b,nabla_w)def evaluate(self,test_data):"""argmax返回的是a中元素最大值所对应的索引值"""# test_results=[(np.argmax(self.feedforward(x),y)) for x,y in test_data] test_results=[(self.feedforward(x),y) for x,y in test_data] return sum(int(compare_float(x,y,0.001)) for x,y in test_results)def cost_derivative(self,output_activations,y):"""loss函数的导数 loss=1/2 * (y^ - y)^2"""return (output_activations)def compare_float(a, b, precision):if abs(a - b) <= precision:return 1return 0def sigmoid(x):return 1.0/(1.0+np.exp(-x))"""sigmoid的导数"""
def sigmoid_prime(x):return sigmoid(x)*(1-sigmoid(x))4.MNIST 数据集
写好代码后我们用测试集测试一下
链接: https://pan.baidu.com/s/1gSeRPwDODK4IeZLVsmPBfQ?pwd=6zcp
提取码: 6zcp
import MNIST.mnist as mnistif __name__=="__main__":dataset=mnist.load_mnist()training_data=dataset[0][0]training_label=dataset[0][1]test_data=dataset[1][0]test_lable=dataset[1][1]net = Network([784,30,1])td=[(np.array(x.copy()),[np.array(y.copy())]) for (x,y) in zip(training_data,training_label)]tt_d=[(np.array(x.copy()),[np.array(y.copy())]) for (x,y) in zip(test_data,test_lable)]net.SGD(td,30,10,3.0,tt_d)
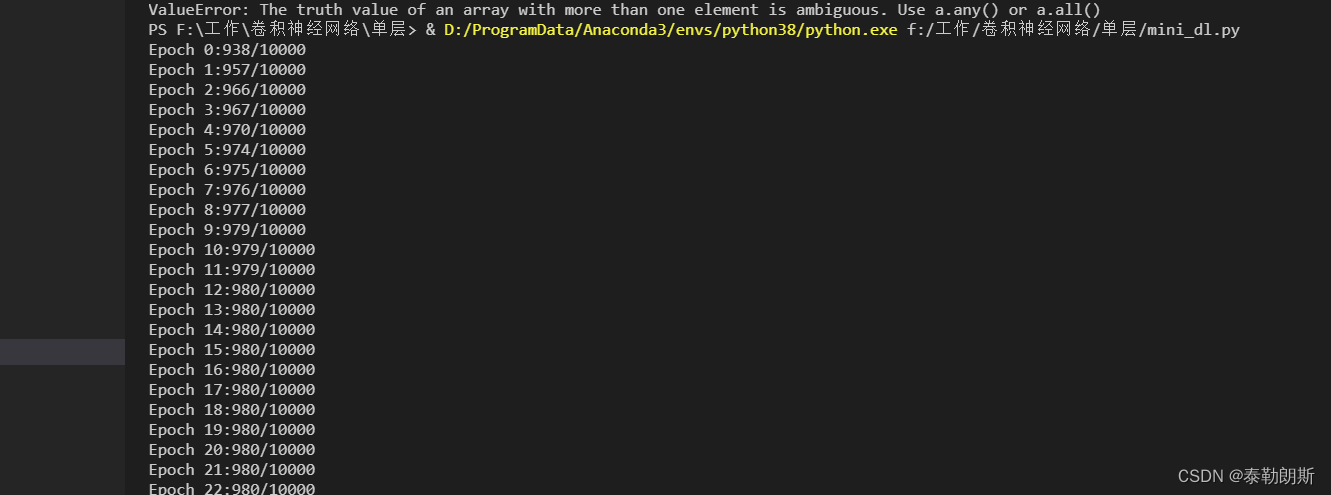
结果如下,可以看到最后精度稳定在98%,还可以:
相关文章:

深度学习-一个简单的深度学习推导
文章目录 前言1.sigmod函数2.sigmoid求导3.损失函数loss4.神经网络1.神经网络结构2.公式表示-正向传播3.梯度计算1.Loss 函数2.梯度1.反向传播第2-3层2.反向传播第1-2层 3.python代码4.MNIST 数据集 前言 本章主要推导一个简单的两层神经网络。 其中公式入口【入口】 1.sigmod…...

ES写入数据报错:retrying failed action with response code: 429
报错: 使用logstash导入分片数量为9的index发生错误,[logstash.outputs.elasticsearch] retrying failed action with response code: 429 ({"type">"es_rejected_execution_exception", "reason">"rejected execution …...

Redis给Lua脚本的调用
Redis给Lua脚本的调用 Redis为Lua提供了一组内置函数,这些函数可用于执行与Redis数据存储和操作相关的任务。这些内置函数可以在Lua脚本中使用,以便在Redis中执行各种操作。以下是一些常用的Redis Lua内置函数: 主要知道call就好了 redis.ca…...

Spring工具类--ReflectUtils的使用
原文网址:Spring工具类系列--ReflectUtils的使用_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Spring的ReflectUtils的使用。 ReflectUtils工具类的作用:便利地进行反射操作。 Spring还有一个工具类:ReflectionUtils,它们在功能上…...

联盟 | 彩漩 X HelpLook,AI技术赋能企业效率提升
近日,AI 驱动的 PPT 协作分享平台「 彩漩 」与 AI 知识库搭建工具「 HelpLook」,携手为用户工作流注入更多智能和创造力,全面拥抱 AIGC 时代带来的机遇,致力于提供前沿的智能解决方案。 彩 漩 彩漩是一个以 AI 技术为基础、贯彻 …...
MATLAB m文件格式化
记录一个网上查到的目前感觉挺好用的格式化方法。 原链接: https://cloud.tencent.com/developer/article/2058259 压缩包: 链接:https://pan.baidu.com/s/1ZpQ9qGLY7sjcvxzjMPAitw?pwd6666 提取码:6666 下载压缩包…...
分拆菜鸟将使阿里巴巴股票迎来新一轮上涨?
来源:猛兽财经 作者:猛兽财经 总结: (1)阿里巴巴(BABA)最近公布的季度财报显示,该公司有能力实现快速盈利。 (2)据报道,阿里巴巴正计划分拆菜鸟集团,并将在香…...

Excel 技巧记录-那些复杂的公式和函数
目标表格的关键字在行和列里,匹配源表格的行和列对应的关键字 **具体需求为:**表A叫Total_202308.xlsx,sheet叫摊销前分析,表B叫data.xlsx,sheet叫总部费用,表A的数据里,A列是科目名称,第9行是…...
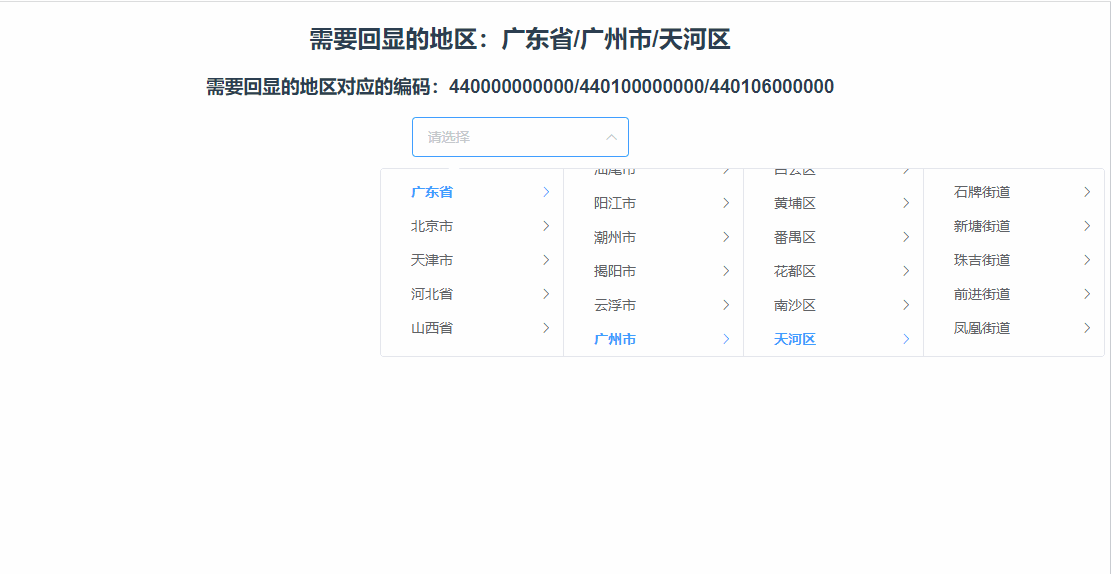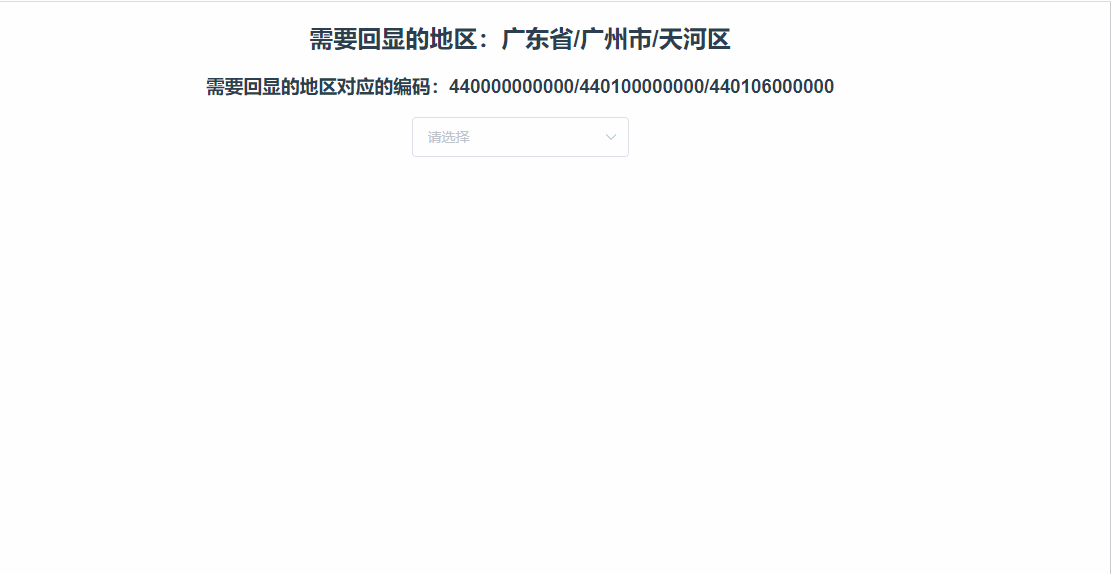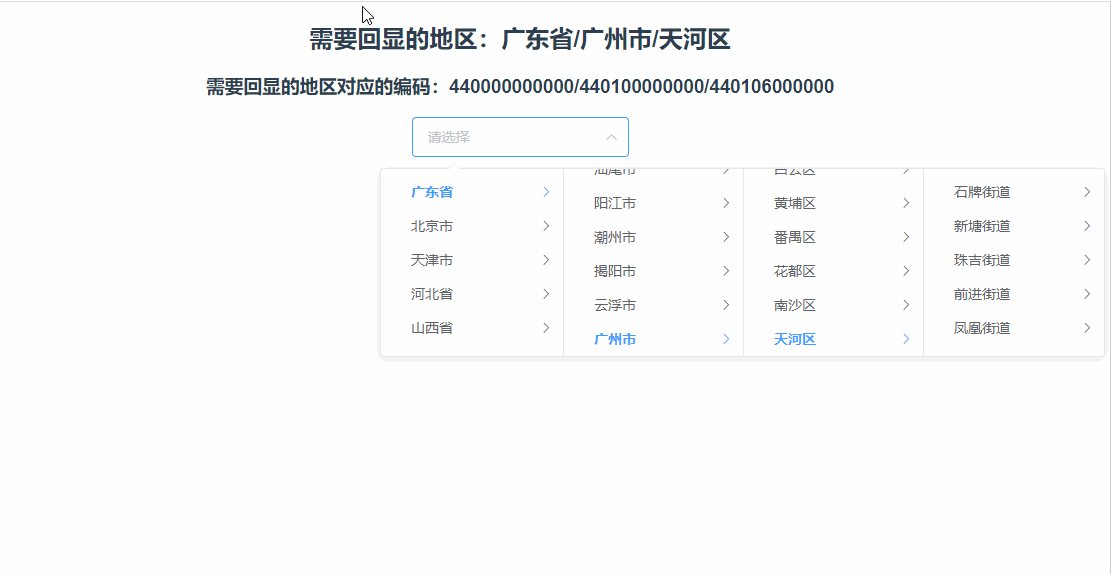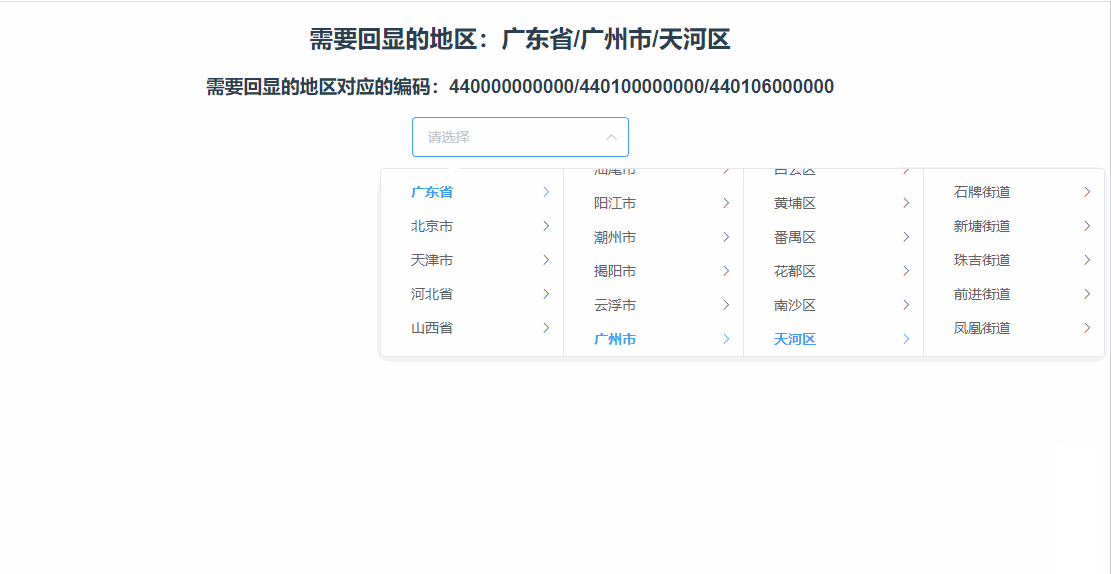
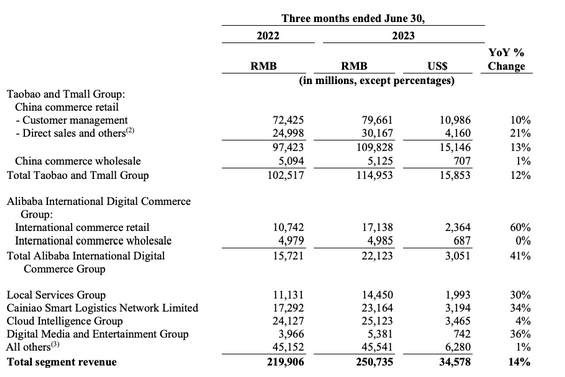
vue里使用elementui的级联选择器el-cascader进行懒加载的怎么实现数据回显?
需要实现的懒加载回显效果 比如:后端返回数据 广东省/广州市/天河区 :440000000000/440100000000/440106000000,需要我们自动展开到天河区的下一级,效果如下 代码实现 我的实现思路就是拿到 440000000000/440100000000/44010600…...
问题)
Qt raise()问题
项目场景: 需要将一个弹窗提升至最前面,那么弹出时直接使用raise()即可。 问题描述: 使用QDialog::raise()时,偶发界面阻塞卡死现象。 原因分析: QDialog::raise()函数是置于顶部的作用,但是如果使用不当…...

26591-2011 粮油机械 糙米精选机
声明 本文是学习GB-T 26591-2011 粮油机械 糙米精选机. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本标准规定了糙米精选机的有关术语和定义、工作原理、型号及基本参数、技术要求、试验方法、检 验规则、标志、包装、运输和储存要求。 …...
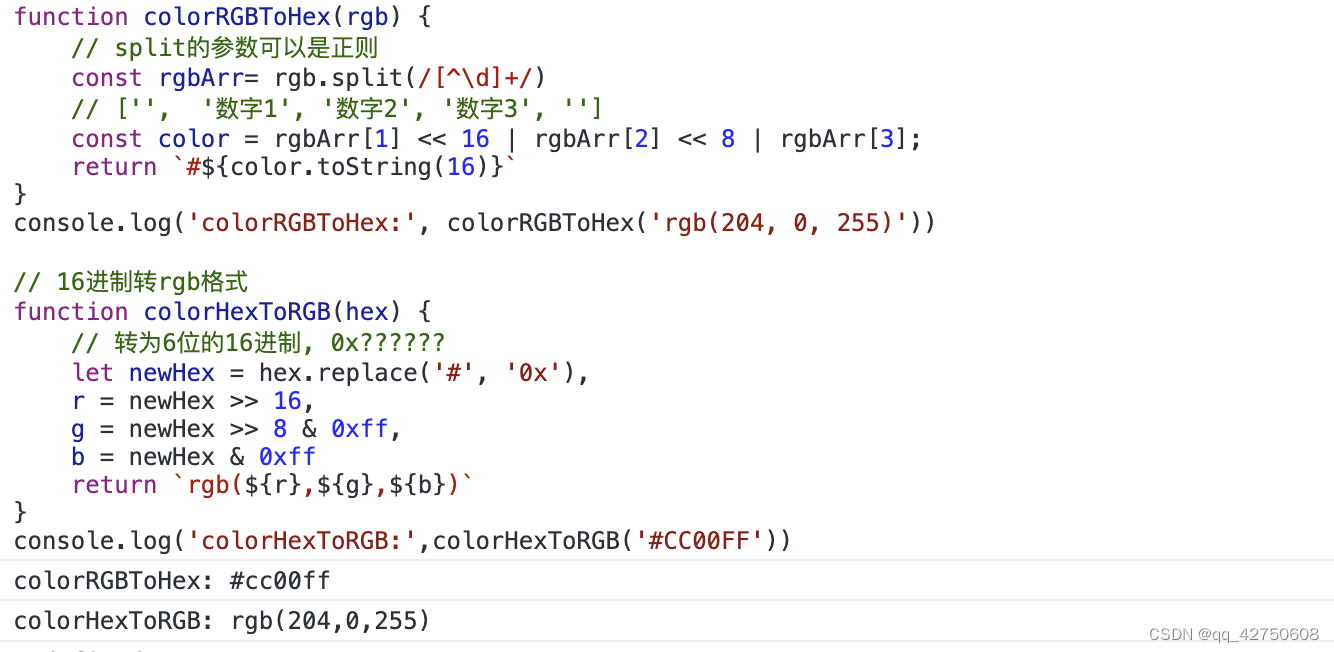
JavaScript位运算的妙用
位运算的妙用: 奇偶数, 色值换算,换值, 编码等 位运算的基础知识: 操作数是32位整数自动转化为整数在二进制下进行运算 一.按位与& 判断奇偶数: 奇数: num & 1 1偶数: num & 1 0 基本知识: 用法:操作数1 & 操作数2规则:有 0 则为…...
This dependency was not found: vxe-table/lib/vxe-table in ./src/main.js
描述 使用时 安装 npm install xe-utils vxe-table 引入 import Vue from vue import xe-utils import VXETable from vxe-table import vxe-table/lib/style.css vxe-table是一个基于 vue 的 PC 端表格组件, 支持增删改查、虚拟滚动、懒加载、快捷菜单、数据校验…...

网工内推 | H3C售前工程师,上市公司,13薪,有带薪年假、年终奖
01 长虹佳华 招聘岗位:高级售前工程师(H3C) 职责描述: 1. 负责公司签约代理的网络安全产品在区域的项目售前技术支持工作,包括项目售前交流、方案编写、招投标、产品测试等相关支持工作; 2. 与厂商产品部门…...
深入理解常见应用级算法思想
1 概论 1.1 概念 1.1.1 数据结构 1)概述 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。 2)划分 从关注的维度…...

Windows下使用pybind11教程(python调用C++代码)
1. 下载pybind11 gittub中下载,pybind下载后解压 2. C生成库文件 2.1.VS新建空白工程,工程名随意起 - 2.2更改目标文件名和配置类型 - 2.3更改目标文件拓展名 2.4添加include路径和库路径 包含目录中添加刚刚下载好的pybind的include路径以及pyhon的…...
基于通用LLM的一次测试用例自动生成的实验
基于通用LLM的一次测试用例自动生成的实验 选择很多,最后选择了讯飞的星火做本次实验,原因还是因为讯飞的LLM的API是有免费额度的,案例代码相对比较成熟易学易用 1 LLM和基于LLM的应用 最近这段实际LLM已经变成了一个炙手可热的词汇,现在任何技术不了到LLM都感觉好像没有彻…...

【excel密码】为什么工作表不能移动、复制了?
为什么excel文件打开之后,工作表里是可以编辑的,但是想要移动工作表或者复制、重命名等操作,这是什么原因?其实这是因为设置了工作簿保护,设置了保护的工作簿无法对整张工作表进行操作。 想要取消这种保护,…...

软考高级之系统架构师之计算机基础
概述 今天是9月28日,距离软考高级只剩37天,加油! 概念 三种周期: Clock Cycle:时钟周期,CPU主频,又称为时钟频率,时钟周期是时钟频率的倒数Instruction Cycle:指令周…...

Mysql生产随笔
目录 1. Mysql批量Kill删除processlist 1.1查看进程、拼接、导出、执行 1.2常见错误解决方案 2.关于时区 3.内存占用优化 记录一下生产过程中的一些场景和命令使用方法,不定期进行更新 1. Mysql批量Kill删除processlist 1.1查看进程、拼接、导出、执行 sho…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
