假设检验的基本思想
假设检验
首先了解参数估计,比如有服从正态分布的数据集X∼N(μ,σ2)X\sim N(\mu,\sigma^{2})X∼N(μ,σ2),我们希望根据样本x1,...xnx_{1},...x_{n}x1,...xn估计出参数μ,σ\mu,\sigmaμ,σ,这些参数可以是一个具体值,也可以是一个范围(即一个区间)。
对于假设检验,分为两种情况:
- 参数假设检验:这种情况下,我们知道总体分布,比如我们已知数据集服从正态分布X∼N(μ,σ2)X\sim N(\mu,\sigma^{2})X∼N(μ,σ2),但参数μ,σ\mu,\sigmaμ,σ我们是不知道的,我们假设μ=μ0,σ=σ0\mu=\mu_{0},\sigma=\sigma_{0}μ=μ0,σ=σ0,现在,我们依然根据样本x1,...xnx_{1},...x_{n}x1,...xn去判断μ\muμ是否等于μ0\mu_{0}μ0,即根据样本判断假设是否成立。
- 非参数假设检验:这是对于分布未知的情况。
总之,假设检验的目的是根据样本判断假设是否成立。
通常存在两种假设,以前面参数假设检验为例:
- 原假设H0H_{0}H0:假设μ=μ0\mu=\mu_{0}μ=μ0;原假设的概率通常较大;
- 备择假设H1H_{1}H1:假设μ≠μ0\mu\neq\mu_{0}μ=μ0;
如果根据样本检验后发现,原假设不成立,备择假设成立,则称[x1,...,xn]∈K0[x_{1},...,x_{n}]\in K_{0}[x1,...,xn]∈K0,样本属于拒绝域K0K_{0}K0。换言之,如果原假设不成立,我们应拒绝原假设。
在拒绝域中的样本才能判断出假设不成立,如果样本不在拒绝域中,我们才能接受原假设。
我们根据样本判断假设,但存在局限性,因为样本数量有限,样本数量多只能降低检验出错的概率,不能代表检验结果完全正确。因此假设检验应考虑到两种错误:
- 原假设成立,但检验后却拒绝了原假设,即弃真错误;
我们把概率P{拒绝H0∣H0成立}=αP\left\{拒绝H_{0}|H_{0}成立\right\}=\alphaP{拒绝H0∣H0成立}=α,α\alphaα称为显著性水平,通常,α\alphaα的值是很小的。如果样本落在拒绝域内的概率P{[x1,...,xn]∈K0}≤αP\left\{[x_{1},...,x_{n}]\in K_{0}\right\}\leq\alphaP{[x1,...,xn]∈K0}≤α,我们就接受原假设,因为此时检验出错的概率已经很低。
反过来,如果P{[x1,...,xn]∈K0}>αP\left\{[x_{1},...,x_{n}]\in K_{0}\right\}>\alphaP{[x1,...,xn]∈K0}>α,我们应当拒绝原假设。 - 原假设不成立,但检验后接受了原假设,即取伪错误;
p-value
p值是假设检验中,判断是否要拒绝原假设的指标,p值是一个概率。
p值:原假设正确时,样本观测值取得某一结果(以及比这个结果更极端结果)的概率。
举例:判断硬币是否公平(出现正面的概率为50%)
原假设:抛硬币结果为正面的概率为50%;
备择假设:抛硬币结果为正面的概率不为50%;
样本,抛硬币500次,正面出现次数10次,反面出现490次。
对于抛硬币500次,整体应服从二项分布:
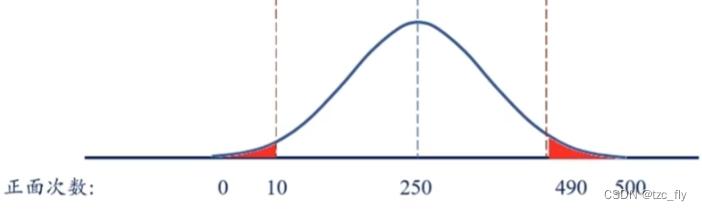
因此,在原假设正确时,预期应该是250次正面,然而实际情况是10次正面,比该结果更极端的情况是正面次数为0次-9次。
另外,如果正面出现超过490次也属于极端情况,因此,图中红色区域表示当前结果以及极端结果。
p值就是图中红色区域对应的概率(面积)。如果p值很小,则意味着,在原假设正确的情况下,小概率事件发生了,比如p值只有1%,即我们只有1%的概率得到目前的观测结果,既然小概率事件发生,我们就有更大概率怀疑这个原假设,因此我们可以拒绝原假设。
通常,只要p值小于显著性水平α\alphaα,我们就拒绝原假设。
相关文章:

假设检验的基本思想
假设检验 首先了解参数估计,比如有服从正态分布的数据集X∼N(μ,σ2)X\sim N(\mu,\sigma^{2})X∼N(μ,σ2),我们希望根据样本x1,...xnx_{1},...x_{n}x1,...xn估计出参数μ,σ\mu,\sigmaμ,σ,这些参数可以是一个具体值,也可以…...

c语言机试练习
1.打印日期 给出年分m和一年中的第n天,算出第n天是几月几号。 输入描述: 输入包括两个整数y(1<y<3000),n(1<n<366)。 输出描述: 可能有多组测试数据,对于每组数据, 按 yyyy-mm-dd的格式将输入中…...
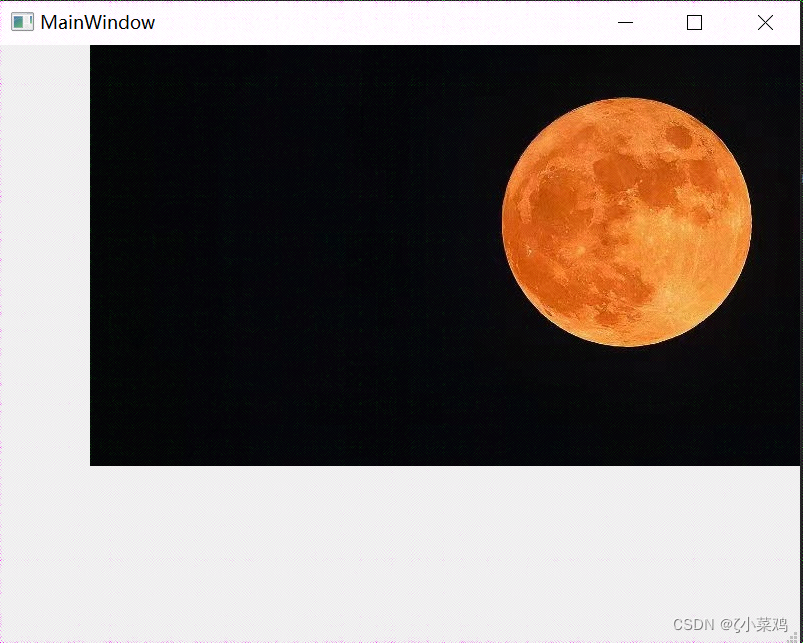
Python的PyQt框架的使用-资源文件夹的使用
Python的PyQt框架的使用-资源文件夹的使用一、前言二、Qt Designer加载资源文件三、资源文件的转换一、前言 个人主页: ζ小菜鸡大家好我是ζ小菜鸡,小伙伴们,让我们一起来学习Python的PyQt框架的使用。如果文章对你有帮助、欢迎关注、点赞、收藏(一键三…...

如何遍历HashMap
文章目录1.Iterator EntrySet2.Iterator keySet3.forEach EntrySet4.forEach keySet5.lambda6.Streams API单线程7.Streams API 多线程1.Iterator EntrySet Iterator<Map.Entry<Integer,String>> iteratormap.entrySet().iterator; while(iterator.hasNext()){Map…...
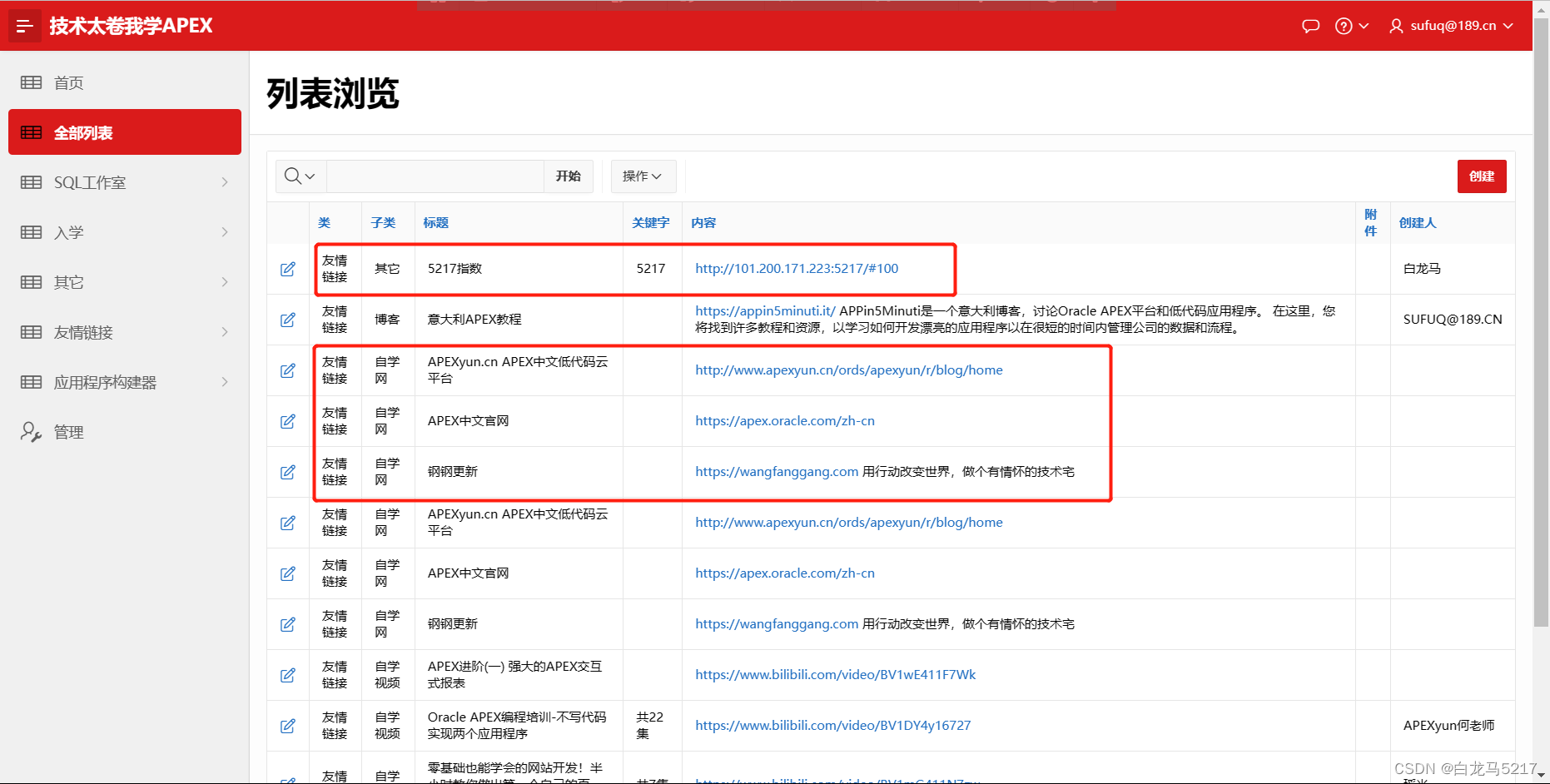
11技术太卷我学APEX-数据加载
11技术太卷我学APEX-数据加载 0 所谓的数据加载 就是导入数据到数据库表中,本示例就采用Excel导入数据到《技术太卷我学APEX》的apex_learn表。表结构大概是这样的 CREATE TABLE "APEX_LEARN" ( "P_ID" NUMBER(17,0) NOT NULL ENABLE, &quo…...
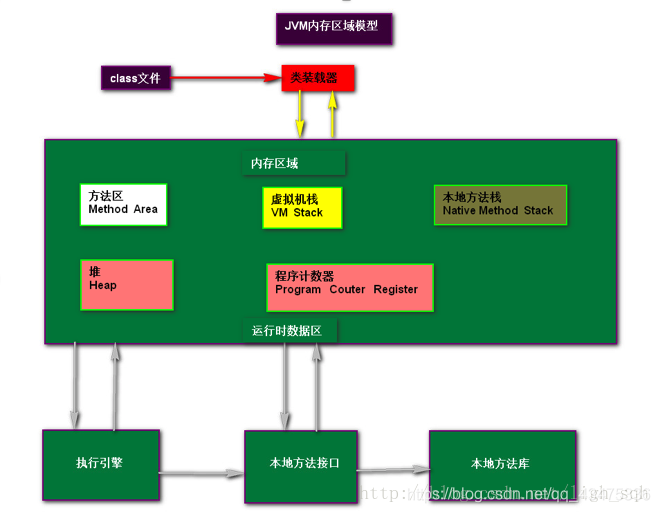
JVM记录
一、JVM体系结构: 类装载器ClassLoader:用来装载.class文件执行引擎:执行字节码,或者执行本地方法运行时数据区:方法区、堆、Java栈、程序计数器、本地方法栈1、方法区: 也称“永久代”,“非堆”…...

盘点机器学习实战中最频繁使用的AutoML工具库
在日常的Kaggle比赛和工作中,经常会遇到AutoML工具。本文总结了常见的AutoML库,可供大家选择。 LightAutoML 项目链接:https://github.com/sberbank-ai-lab/LightAutoML 推荐指数:⭐⭐⭐ LightAutoML是基于Python环境下的结构…...

50-Jenkins-Lockable Resources插件实现资源锁定
Lockable Resources插件实现资源锁定前言安装插件使用插件资源配置Pipeline中使用前言 用来阻止多个构建在同一时间试图使用同一个资源。这里的资源可能是一个节点、一个代理节点、一组节点或代理节点的集合,或者仅仅是一个用于上锁的名字。如果指定的资源没有在全…...

测试员,如果未来5年你不想失业……你得学会自动化测试
工作中总会遇到各种各样的无常,这边测试工具的工作你刚刚接手,那边又临时紧急插播一个接口测试任务,这对于测试老鸟来说已然是常态,但对新手来说却是个挑战。 不得不承认,工作就是在无限的变化和挑战中不断的磨炼我们…...

腾讯开源的 hel 提供了加载远程模块的能力,谈谈它的实现原理
腾讯开源的 hel,提供了一种运行时引入远程模块的能力,模块部署在 CDN,远程模块发布后,不需要重新构建发布,就能生效。 个人觉得它的实现原理非常的不错,因此分享给大家。 远程模块可以作为微模块…...
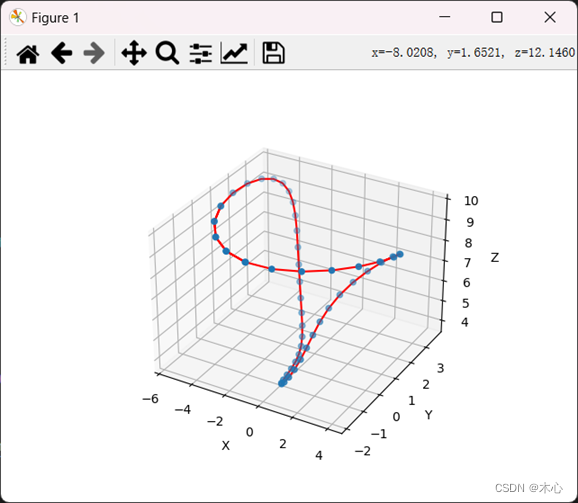
【运动控制】CNC三轴小线段路径规划
CNC三轴小线段路径规划 文章目录CNC三轴小线段路径规划一、项目说明二、具体实现1、速度规划2、小线段插补3、运动学逆解刀轴插补点4、差分处理得到实际的速度和加速度5、加速度滑动平均6、实现的效果如图所示三、Reference写在前面,本文是作为一个练手小项目的总结…...

渗透测试之DNS域名信息探测实验
渗透测试之DNS域名信息探测实验实验目的一、实验原理1.1 域名1.2 .域名的构成1.3 域名的基本类型1.4 域名级别二、实验环境2.1 操作机器三、实验步骤1. 使用sp查询域名信息2. 进行探测实验实验目的 掌握使用nslookup进行DNS域名信息探测的原理和方式了解子域名查询网站 一、实…...

ASE140N04-ASEMI低压MOS管ASE140N04
编辑-Z ASE140N04在TO-220F封装里的静态漏极源导通电阻(RDS(ON))为4mΩ,是一款N沟道低压MOS管。ASE140N04的最大脉冲正向电流ISM为400A,零栅极电压漏极电流(IDSS)为1uA,其工作时耐温度范围为-55~175摄氏度。ASE140N04…...
Qt——QLineEdit
QLineEdit是一个单行文本编辑控件。 使用者可以通过很多函数,输入和编辑单行文本,比如撤销、恢复、剪切、粘贴以及拖放等。 通过改变QLineEdit的 echoMode() ,可以设置其属性,比如以密码的形式输入。 文本的长度可以由 maxLength(…...

前端-HTML-zxst
HTML HTML是超文本标记语言(HyperText Mark-up Language) CSS是层叠样式表(Cascading Style Sheets) JS,即JavaScript是一种具有函数优先的轻量级,解释型或即时编译型的编程语言 <!--doctype标签声明…...

终极方案,清理 docker 占用磁盘过大问题, 亲测有效!
背景 在笔者的工作测试环境中,使用过程中突然出现根磁盘快吃满了(docker也是使用的根池盘的/var/lib/docker), wtf ? 服务用不了? 当然网上找到了一些常规的清楚docker 日志文件 但是通过df -hT 查看到over…...

puzzle(1321)时间旅人
时间旅人 最强大脑同款项目。 每个指针会带动周围2圈指针一起带动,内圈8个旋转180度,外圈16个旋转90度,全部调整为朝上则胜利。 问题本质: 很明显,问题本质就是求每个格子的点击次数,最少为…...

活动预告 | 2023 Meet TVM 开年首聚,上海我们来啦!
内容一览:从去年 12 月延期至今的 TVM 线下聚会终于来了!首站地点我们选在了上海,并邀请到了 4 位讲师结合自己的工作实践,分享 TVM 相关的开发经验,期待与大家线下相聚~ 关键词:2023 Meet TVM 线下活动 自…...

CoreIDRAW 软件的强大功能及适用性
1.1 绘图功能CoreIDRAW 软件是一种特殊的设计软件和图形绘制软件,使用方便、功能强大,在网页效果、商业插画设计、海报广告设计、平面设计等各类行业中都得到广泛的应用,在服装设计行业中,也逐渐地投入使用。由于纺织服装行业在设…...

JavaScript Window History
在 Web 开发中,JavaScript Window History(浏览器窗口历史记录)是一个非常有用的对象,它提供了一个接口来与浏览器历史记录进行交互。JavaScript Window History 对象允许您访问当前会话的历史记录,以及在会话历史记录…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
